Учебно-методический материал по математике (1 класс) на тему: нестандартные задачи 1 класс по математике
Занятие 1. НУМЕРАЦИЯ ЧИСЕЛ В ПРЕДЕЛАХ 10
I. «Поспевай – не зевай»
(Учитель читает вопрос, дети должны быстро давать ответ,
не поднимая руки.)
1. Когда падает снег? (Зимой.)
2. Самое большое однозначное число? (9.)
3. Сколько дней в неделе? (7.)
4. Кто первый тянул репку? (Дед.)
5. С чего начинается дружба? (С улыбки.)
6. Какой гриб растет под березой? (Подберезовик.)
7. Сколько букв в русском алфавите? (33.)
8. Задача:
К серой цапле на урок
Прилетели 7 сорок,
А из них лишь 3 сороки
Приготовили уроки.
Сколько лодырей-сорок
Прилетело на урок? (4.)
II. Решите задачи
1. Какие числа надо переставить, чтобы они шли в порядке
возрастания: 1, 2, 3, 5, 4, 6, 8, 7, 9?
(Ответ: надо переставить числа 5 и 4, а также 8 и 7.)
2. Петя, возвратившись с прогулки, подбежал к маме и стал
рассказывать: «А мы видели разных птиц: голубя, скворца, бабоч-
ку, воробья, сороку, стрекозу и грача. Вот сколько – целых семь
штук!» Мама заметила, что Петя ошибся, и сказала ему об этом.
В чем Петина ошибка? Сколько всего он видел птиц?
(Ответ: всего Петя видел 5 птиц.)
3. Два товарища договорились ехать вместе в пятом вагоне
электропоезда. Электропоезд состоял из девяти вагонов. Один из
6 Нестандартные задачи по математике. 1 класс
товарищей сел в пятый вагон с начала, а другой – в пятый вагон
с конца. В один ли вагон сели товарищи?
(Решение. Они сели в один вагон. Для того чтобы это про-
верить, можно сделать соответствующий рисунок. Если хотим
ответить на вопрос без использования рисунка, то можно вначале
назвать пять номеров вагонов, считая с начала: первый, второй,
третий, четвертый, пятый, а затем назвать пять номеров вагонов,
начиная с конца электропоезда: девятый, восьмой, седьмой, шес-
той, пятый. Таким образом, если бы вагоны были пронумерова-
ны, то друзья ехали бы в вагоне № 5.)
4. Электропоезд состоял из 8 вагонов. Пассажир с собакой
сел в четвертый вагон от начала поезда, а пассажирка с кошкой
села в четвертый вагон от конца поезда. В одном ли вагоне ехали
кошка с собакой?
(Решение. Они ехали в разных вагонах. Рассуждая таким же
образом, что и в предыдущей задаче, назовем четыре номера ва-
гонов, начиная с конца: восьмой, седьмой, шестой, пятый. Таким
образом, пассажир с собакой ехал в четвертом вагоне от начала по-
езда, а пассажирка с кошкой – в пятом вагоне от начала поезда.)
III. Игра
У ч и т е л ь. Я назову какое-либо число, а вы назовите мне
такой предмет, который содержит это число. Например, если
я скажу «пять», вы можете ответить: «Рука имеет пять пальцев».
Или: «На руке пять пальцев».
(Можно организовать такую игру между двумя учащимися,
а можно между одним и всеми остальными, причем если задаю-
щий называет число «один» или «два», то отвечающий должен
дать ответ в мужском роде – «1 рубль», «два глаза» или «два уха
у человека», а если «одна», «две», то отвечающий говорит, на-
пример, «одна голова у коня», «две ноги у курицы». Надо иметь
в виду, что такую игру легче организовать в пределах первой
пятки, чем в пределах второй пятки.)
Занятие 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ЧИСЕЛ
В ПРЕДЕЛАХ 10
I. «Поспевай – не зевай»
1. К какому числу надо прибавить 2, чтобы получилось 10? (8.)
2. Что в хлебе родится, а есть не годится? (Василек.)
Занятие 2. Сложение и вычитание чисел в пределах 10 7
3. Тише едешь – … (дальше будешь).
4. Лыко дерет, а лапти не носит. (Коза.)
5. Сколько звуков в слове «юла»? (4.)
6. Паук – насекомое или нет? (Нет.)
7. В каком слове 7 «я»? (Семья.)
8. Задача:
Повезло опять Егорке.
У реки стоит не зря –
Пять карасиков в ведерке
И четыре пескаря.
Сколько рыбок он поймал? (9 рыб.)
II. Решение задач
1. а) К одному числу прибавили другое число, получилось
число, равное первому. Сколько прибавили? б) К одному числу
прибавили другое число, получилось число, равное второму чис-
лу. К какому числу прибавили второе число? в) Из одного числа
вычли другое число, получилось первое число. Какое число вы-
чли? г) Из одного числа вычли другое число, осталось столько,
сколько вычли. Придумайте такие примеры.
(Ответ: а) прибавили 0; б) прибавили к 0; в) вычли 0; г) вы-
чли половину уменьшаемого, например 12 – 6 = 6.)
2. В магазине за день купили 8 холодильников. Сколько по-
требуется сделать рейсов, чтобы доставить все купленные хо-
лодильники, если на машину можно погрузить только 3 холо-
дильника?
(Ответ: 3 рейса. 8 = 3 + 3 +2.)
3. По рецепту врача для больного купили в аптеке 10 табле-
ток. Врач прописал принимать лекарство по 3 таблетки в день.
На сколько дней хватит этого лекарства?
(Решение. Будем прибавлять по три: 3 + 3 + 3 +1 = 10. На
четвертый день останется только одна таблетка, следовательно,
лекарства хватит на 3 дня.)
4. Гриша из большого листа бумаги сделал себе блокнот. Он
сложил лист вдвое – получил 2 листа, затем перегнул эти лист-
вы пополам, а затем еще раз перегнул их пополам. Из скольких
листов состоял блокнот у Гриши?
(Решение. При сложении листа пополам число листов
будет удваиваться, т. е. будет прибавляться столько листов,
сколько получилось на данный момент времени: а) 1 + 1 = 2;
СОДЕРЖАНИЕ
Учебно-методическое пособие по математике (1 класс) на тему: Нестандартные задачи по математике 1 класс
Занятие 1. НУМЕРАЦИЯ ЧИСЕЛ В ПРЕДЕЛАХ 10
I. «Поспевай – не зевай»
(Учитель читает вопрос, дети должны быстро давать ответ,
не поднимая руки.)
1. Когда падает снег? (Зимой.)
2. Самое большое однозначное число? (9.)
3. Сколько дней в неделе? (7.)
4. Кто первый тянул репку? (Дед.)
5. С чего начинается дружба? (С улыбки.)
6. Какой гриб растет под березой? (Подберезовик.)
7. Сколько букв в русском алфавите? (33.)
8. Задача:
К серой цапле на урок
Прилетели 7 сорок,
А из них лишь 3 сороки
Приготовили уроки.
Сколько лодырей-сорок
Прилетело на урок? (4.)
II. Решите задачи
1. Какие числа надо переставить, чтобы они шли в порядке
возрастания: 1, 2, 3, 5, 4, 6, 8, 7, 9?
(Ответ: надо переставить числа 5 и 4, а также 8 и 7.)
2. Петя, возвратившись с прогулки, подбежал к маме и стал
рассказывать: «А мы видели разных птиц: голубя, скворца, бабоч-
ку, воробья, сороку, стрекозу и грача. Вот сколько – целых семь
штук!» Мама заметила, что Петя ошибся, и сказала ему об этом.
В чем Петина ошибка? Сколько всего он видел птиц?
(Ответ: всего Петя видел 5 птиц.)
3. Два товарища договорились ехать вместе в пятом вагоне
электропоезда. Электропоезд состоял из девяти вагонов. Один из
6 Нестандартные задачи по математике. 1 класс
товарищей сел в пятый вагон с начала, а другой – в пятый вагон
с конца. В один ли вагон сели товарищи?
(Решение. Они сели в один вагон. Для того чтобы это про-
верить, можно сделать соответствующий рисунок. Если хотим
ответить на вопрос без использования рисунка, то можно вначале
назвать пять номеров вагонов, считая с начала: первый, второй,
третий, четвертый, пятый, а затем назвать пять номеров вагонов,
начиная с конца электропоезда: девятый, восьмой, седьмой, шес-
той, пятый. Таким образом, если бы вагоны были пронумерова-
ны, то друзья ехали бы в вагоне № 5.)
4. Электропоезд состоял из 8 вагонов. Пассажир с собакой
сел в четвертый вагон от начала поезда, а пассажирка с кошкой
села в четвертый вагон от конца поезда. В одном ли вагоне ехали
кошка с собакой?
(Решение. Они ехали в разных вагонах. Рассуждая таким же
образом, что и в предыдущей задаче, назовем четыре номера ва-
гонов, начиная с конца: восьмой, седьмой, шестой, пятый. Таким
образом, пассажир с собакой ехал в четвертом вагоне от начала по-
езда, а пассажирка с кошкой – в пятом вагоне от начала поезда.)
III. Игра
У ч и т е л ь. Я назову какое-либо число, а вы назовите мне
такой предмет, который содержит это число. Например, если
я скажу «пять», вы можете ответить: «Рука имеет пять пальцев».
Или: «На руке пять пальцев».
(Можно организовать такую игру между двумя учащимися,
а можно между одним и всеми остальными, причем если задаю-
щий называет число «один» или «два», то отвечающий должен
дать ответ в мужском роде – «1 рубль», «два глаза» или «два уха
у человека», а если «одна», «две», то отвечающий говорит, на-
пример, «одна голова у коня», «две ноги у курицы». Надо иметь
в виду, что такую игру легче организовать в пределах первой
пятки, чем в пределах второй пятки.)
Занятие 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ЧИСЕЛ
В ПРЕДЕЛАХ 10
I. «Поспевай – не зевай»
1. К какому числу надо прибавить 2, чтобы получилось 10? (8.)
2. Что в хлебе родится, а есть не годится? (Василек.)
Занятие 2. Сложение и вычитание чисел в пределах 10 7
3. Тише едешь – … (дальше будешь).
4. Лыко дерет, а лапти не носит. (Коза.)
5. Сколько звуков в слове «юла»? (4.)
6. Паук – насекомое или нет? (Нет.)
7. В каком слове 7 «я»? (Семья.)
8. Задача:
Повезло опять Егорке.
У реки стоит не зря –
Пять карасиков в ведерке
И четыре пескаря.
Сколько рыбок он поймал? (9 рыб.)
II. Решение задач
1. а) К одному числу прибавили другое число, получилось
число, равное первому. Сколько прибавили? б) К одному числу
прибавили другое число, получилось число, равное второму чис-
лу. К какому числу прибавили второе число? в) Из одного числа
вычли другое число, получилось первое число. Какое число вы-
чли? г) Из одного числа вычли другое число, осталось столько,
сколько вычли. Придумайте такие примеры.
(Ответ: а) прибавили 0; б) прибавили к 0; в) вычли 0; г) вы-
чли половину уменьшаемого, например 12 – 6 = 6.)
2. В магазине за день купили 8 холодильников. Сколько по-
требуется сделать рейсов, чтобы доставить все купленные хо-
лодильники, если на машину можно погрузить только 3 холо-
дильника?
(Ответ: 3 рейса. 8 = 3 + 3 +2.)
3. По рецепту врача для больного купили в аптеке 10 табле-
ток. Врач прописал принимать лекарство по 3 таблетки в день.
На сколько дней хватит этого лекарства?
(Решение. Будем прибавлять по три: 3 + 3 + 3 +1 = 10. На
четвертый день останется только одна таблетка, следовательно,
лекарства хватит на 3 дня.)
4. Гриша из большого листа бумаги сделал себе блокнот. Он
сложил лист вдвое – получил 2 листа, затем перегнул эти лист-
вы пополам, а затем еще раз перегнул их пополам. Из скольких
листов состоял блокнот у Гриши?
(Решение. При сложении листа пополам число листов
будет удваиваться, т. е. будет прибавляться столько листов,
сколько получилось на данный момент времени: а) 1 + 1 = 2;
СОДЕРЖАНИЕ
Нестандартные задачи для 1-2 классов.

Нестандартные задачи
Математика
1-2 классы

1. Портфель Коли помещается в портфеле Васи, а портфель Васи можно спрятать в портфель Севы. Какой из этих портфелей самый большой?
К
В
С

2. Температура тела у человека меньше температуры тела голубя, но больше, чем у слона. У кого из них термометр покажет самую низкую температуру?
Г
Ч
С

3. Если провести более твердым по менее твердому, то на менее твердом может остаться след, царапина. Останется ли царапина, если провести стеклом по картону? Картоном по стеклу?
Стекло оставит царапину на картоне, так как оно тверже; картон не оставит царапины на стекле, так как стекло тверже картона.

4. Если провести стеклом по мрамору, на мраморе окажется царапина. А если провести алмазом по стеклу, царапина останется на стекле. Какой из этих материалов самый твердый?
1) Стекло тверже мрамора, так как оставляет на нем царапину. 2) Алмаз тверже стекла, так как оставляет на нем царапину. 3) Следовательно, алмаз самый твердый из этих трех веществ.

5. Мама дала по яблоку трем своим детям. Катино яблоко тяжелее, чем Петино, а Петино легче, чем Васино. Какое яблоко самое большое, а какое самое маленькое?
В
В
П
П
К
К
П
В
К

3. Сколько весит арбуз?
Решение : 10 – (1 + 3) = 6 (кг).

2. Шесть пирожных разделили между братьями и сестрами так, что у братьев их оказалось на два меньше, чем у сестер. Сколько у кого?
1) Сколько было бы пирожных, если бы у сестер было столько же, сколько у братьев? 6 – 2 = 4.
2) Сколько было пирожных у братьев? 4 : 2 = 2.
3) Сколько было пирожных у сестер? 2 + 2 = 4

3. Ваня живет в 12-этажном доме, на 9 этаже, если считать сверху. На каком этаже живет Ваня?
1) С колько этажей дома находится ниже Вани?
12 – 9 = 3
Ответ : На 4 этаже.

3. Ваня живет в 12-этажном доме, на 9 этаже, если считать сверху. На каком этаже живет Ваня?
1) С колько этажей дома находится ниже Вани?
12 – 9 = 3
Ответ : На 4 этаже.

4. В коробке лежит 15 шариков: черных, белых и красных. Красных шариков в 7 раз больше, чем белых. Сколько в коробке черных шариков?
Белых шариков не может быть больше одного,
так как если бы их было хотя бы 2,
то красных шариков было бы не меньше 14,
а шариков всего 15.
Значит, белый шарик всего один , а красных в семь раз больше, то есть семь . Черных шариков 15 – (1 + 7) = 7.

5. Пес Тузик на 6 кг тяжелее кота Барсика, а Барсик втрое легче Тузика. Сколько весит Барсик?
Решение : 6 : 2 = 3 (кг).
Б
6
Т

7. Придумай возможное продолжение этой последовательности чисел:
1, 1, 2, 3, 5,…
8, 13, 21
Решение. 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5

1. Поставь точки по образцу. Начерти прямоугольник, который проходит через все эти точки. Найди его периметр и площадь, если 1 клетка – это 1 см.

1. Поставь точки по образцу. Начерти прямоугольник, который проходит через все эти точки. Найди его периметр и площадь, если 1 клетка – это 1 см.

Интернет ресурсы
https://img-fotki.yandex.ru/get/3610/39663434.8ed/0_acde1_2dd5b215_XL.png
https :// img-fotki.yandex.ru/get/9115/39663434.8ed/0_acddd_9684dbb5_XL.png
Использован шаблон учителя русского языка и литературы Тихоновой Надежды Андреевны, г.Кустанай
Разработка урока математики в 1-м классе «Решение нестандартных примеров и задач»
Цели:
- Познакомить учащихся с различными видами нестандартных примеров и задач и их решением путём рассуждения, используя схемы, рисунки.
- Развивать учебно-логические умения.
- Активизировать познавательную деятельность учащихся. Повышать интерес к математике через занимательный математический материал и нестандартную форму проведения занятия. Воспитывать чувство коллективизма, долга, ответственности за свою команду, желание достигнуть высоких результатов не только у себя, но и у товарищей.
Тип урока: изучение нового материала
ФОПД: фронтальная, групповая, работа в парах.
Методы: словесный, наглядный, частично-поисковый, метод стимулирования учебной деятельности.
Оборудование:
- Карточки с деформированными пословицами
- Ребус со словом задача
- Имена 4 детей на карточках и 4 различных по размеру нарисованных мяча
- Примеры на карточках.
Ход урока
I. Организация класса.
II. Математическая разминка
– Чтобы вам быстрее включиться в работу проведём математическую разминку.
а) Загадка
Братцев этих ровно 7
Вам они известны всем.
Каждую неделю кругом
Ходят братцы друг за другом.
Ответ: 7 дней недели.
б) Задача в стихах
«В гнёздышке есть 2 птенца
Два пушистых близнеца,
И ещё готовы 5
Из скорлупок вылезать.
– Сколько станет птиц в гнезде?
Помогите мне.
Ответ: 2+5=7
в) Закономерность
– Белка свои орешки разложила кучками в определённой последовательности, а некоторые числа, обозначающие количество орешков закрыла листьями. Отгадайте закономерность.
Ответ: 1 5 9 13 17 21
г) Задание на внимание и быстроту счёта
– Чему равна сумма чисел, записанных красным цветом? синим?
– Что вы заметили? (Суммы = 13)
– Что вы знаете о числе 13?
– Число 13 многие люди считают несчастливым, а в Англии нет даже №13 на квартирах.
Работа в группах
д) «Пословицы»
– Сейчас поработаем в группах. Какая же группа работает сплочённее, помогая друг другу.
– Составьте правильно пословицы, где дано начало, а ват продолжение пословицы вам нужно выбрать. Соедините начало и конецпословицы стрелкой.
| Семеро одного | не ждут приведут подождут | |
| Семь раз отмерь | 7 раз примерь 7 раз отрежь 1 раз отрежь |
– Объясните смысл пословиц.
– Как вы думаете, почему эти пословицы я включила в урок?
– Что общего у них? (Число 7)
– Дети отвечают (они связаны с математикой и числом 7)
– Особым почётом в древности была окружена семёрка, это дошло и до наших дней.
- Много пословиц и поговорок связано с числом 7.
- Сейчас 7 дней в неделе,
- 7 чудес света,
- Великий пост у христиан 7 дней.
- Считалось, что 7 символизирует тайну. Вначале урока была задача и загадка с числом 7.
– Сколько вариантов ответов было в карточках (3)
– Ребята, а где вы встречаете число 3 в жизни?
Дети отвечают:
– (В сказках: 3 сестрицы под окном – авторская сказка, 3 желания у рыбки, 3 сына у отца, 3 поросёнка, 3 медведя)
– Долгое время число 3 для многих народов считалось счастливым числом. Оно стало излюбленным в мифах и сказках, считалось магическим, так как складывалось из суммы предыдущих чисел (2+1)
Итог разминки:
– Математическая разминка закончена. Помимо того, что вы уже включились в работу, вы ещё узнали интересное о числах 3, 7 и 13.
III. Сообщение темы урока и постановка темы
– Ребята, отгадав этот ребус, вы узнаете тему занятия.
Задача
– Правильно, ребята, задача.
– Тема урока: «Решение нестандартных задач и примеров»
– Как вы понимаете слово «нестандартные»?
– К нестандартным относят логические задачи, задачи на смекалку, задачи-шутки, зашифрованные примеры.
– Зная тему урока, давайте попытаемся поставить цель нашего занятия, то есть чего мы будем добиваться (дети говорят: будем учиться решать задачи и примеры)
– А для чего нам нужно решать такие задачи и примеры?
– Да, такие задания учат размышлять, решать проблему, анализировать — это всё развивает логическое мышление.
Учитель читает задачу:
«Четыре девочки с детского сада, Аня, Варя, Галя, Зина – играли с мячами. Затем их позвали на завтрак. Мячи они положил в уголке. Которым из них играла каждая девочка, если мяч Вари не самый маленький, но он меньше, чем у Ани и Зины, а у Ани больше чем у Зины?»
- Давайте прочитаем задачу ещё раз и выделим те данные, которые помогут в решении.
- Нам известно, что есть четыре девочки с мячами. Их зовут Аня, Варя, Галя и Зина.
- Выделите и подчеркните в тексте главные слова.
- Что из условия задачи вам стало понятно про мячи?
- Какие они по размеру? (различные)
- Есть ли среди них одинаковые? ( нет)
- Предположим, что их нет и все мячи разные.
- Чтобы нам не запутаться при решении задачи имена девочек я записала на карточках и приготовила различные мячи.
- Решать логические задачи можно при помощи рисунка, таблицы, схемы. Сегодня мы будем решать при помощи схемы.
- Имена девочек написаны на карточках, а ниже произвольно-прикреплённые изображения мячей разных размеров и цветов.
- Что известно о мячах?
- Мяч Вари не самый маленький… А какой среди мячей самый маленький?
- Он может быть мячом Вари? (Нет)
- Значит, будем искать её мяч из трёх оставшихся.
- Мы знаем, что мяч Вари меньше, чем Ани и Зины?
- Какой мяч меньше?
- Это мяч Вари. Рисуем стрелкой, что он принадлежит ей.
- Разбираем задачу дальше.
- Мы знаем, что у Ани мяч больше, чем у Зины.
- Какой из оставшихся двух больше?
- Это мяч Ани, чертим стрелочку.
- Тот, который чуть меньше – это мяч Зины.
- Чей тогда самый маленький оставшийся мяч? (Гали)
- Путём рассуждения мы определили какие мячи принадлежат трём девочкам, а тот который остался – это и есть мяч Гали.
- Вы ответили на вопрос задачи? (Да)
- Что помогло нам в решении (схема)
- В уме представить кому из девочек принадлежал какой мяч трудно. Нам помогла схема.
- В другой раз не обязательно писать имена целиком, можно ограничиться буквами, так вы и сделаете у себя в тетради, а мячи изобразите в виде различных кружков.
- Так подтвердилось наше предположение, что мячи разные по размеру?
- Могли ли они быть одинаковыми? (нет)
- Зарисуйте в тетради схему.
IV. Физминутка
игра «Четыре стихии»
Если я говорю земля, вы опускаете руки вниз, если воздух, то поднимаете вверх. Если огонь, то руки приживаете к груди, если вода, то руками изображаете плавающего человека.
V. Работа в группах
– А сейчас попробуйте решить задачу в группах, советуясь, помогая друг другу.
– Решайте, используя схему при решении. Посмотрим, какая из групп окажется дружнее и сплочённее.
Каждой группе даётся задание на карточке.
«В квартирах №1, №2, №3 жили три котёнка: Белый, чёрный и рыжий. В квартирах №1, и 2 не жил чёрный, а белый не жил в квартире №1. В какой квартире жил каждый котёнок?
– О ком говорится в задаче
– Дети, о каких котятах идёт речь?
– В каких квартирах они живут? (1, 2, 3)
– Эти данные используйте в своей схеме.
Итог:
(Проверка решений задачи по группам)
– Логическую задачу представить без рисунка, схемы, таблицы очень трудно. Схема помогает решить задачу. В дальнейшем будем учиться записывать и решать при помощи таблицы.
VI. Решение нестандартных примеров
– Посмотрите на доску. Я приготовила для вас необычные примеры. Сразу их не решить.
– Попробуем разобраться в символах, знаках, фигурах.
21 * Δ = 21
(21 + 0 = 21; 21 – 0 = 21)
– Мы видим два числа, 21 и =21
– Как вы думаете, что может стоять вместо * и Δ
– Да, это знаки и числа
– Здесь может быть ещё 21 · 1 = 21 и 21 : 1 = 21. Но мы ещё не изучали действия умножение и деление.
А вот ещё пример
27 * 1 + Δ 7
– Я зашифровала здесь неравенство
– Тогда какие знаки здесь могут быть? (><)
– Значит вместо * будет знак > или <
– Что запишем вместо Δ? (число)
– Это математическое выражение имеет одно решение? (Нет)
VII. работа в парах
– Расшифруйте и решите примеры
Δ * 40 = 40
11 * Δ = 12 * Δ
Δ * 30 = 23 * Δ
22 * Δ = 23 * Δ
VIII. Итог урока
– Чему учились на уроке?
– Понравилось ли вам решать такие задачи и примеры?
– Что понравилось?
– Достигли ли цели, которую ставили в начале урока?
Нестандартные задачи по математике с решениями. 7-9 класс. Часть 1.
Интерес к математике и математические способности учащихся проявляются в довольно раннем возрасте. Значительную роль в их развитии играет систематическое решение задач, которые могли бы заинтересовать юных математиков и способствовали бы стремлению к самостоятельным исследованиям.
Именно такие задачи содержит данный сборник. Он предназначен для внеклассных занятий с учащимися 7–9 классов.
В сборнике приведены подробные решения 20 нестандартных задач. Многие из них предлагались на математических олимпиадах.
Данный сборник может служить пособием для подготовки учащихся к олимпиадам по математике.
Задача № 1
Доказать, что если из трехзначного числа вычесть трехзначное число, записанное теми же числами, что и первое, но в обратном порядке, то модуль полученной разности будет делится на 9 и 11.
Решение:
Пусть 100a + 10b + c – трехзначное число, тогда 100с +10b + a – трехзначное число, записанное теми же числами, что и первое, но в обратном порядке.
100a + 10b + c – 100с –10b – a = 99а – 99с = 99(а–с)
|99(а–с)| – делится на 9,
|99(а–с)| – делится на 11,
т.к.очевидно, что 99 будет делиться на 9 и на 11.
Задача № 2
Если между цифрами двузначного числа x вписать это же число, то полученное четырехзначное число будет в 66 раз больше первоначального двузначного. Найти х.
Решение:
Пусть 100a + b = х – данное двузначное число, тогда 1000а +100а + 10b + b – полученное четырехзначное число, что по условию равно (10а + b)/66. Имеем уравнение:
1000а +100а + 10b + b = (10а + b)/66;
1100а + 11b = 660а + 66b;
440а = 55b;
8а = b;
а 0, т.к. а – первая цифра двузначного числа;
а = 1, b = 8, следовательно, x = 18.
а = 2, b = 16, что невозможно, т.к. b – вторая цифра двузначного числа.
Итак, искомое число 18.
Задача № 3
Доказать, что число 333555 + 555333 делится на 37.
Решение:
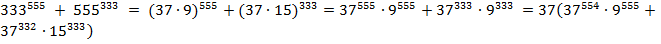 . Очевидно, что
. Очевидно, что 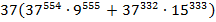 делится на 37.
делится на 37.
Задача № 4
Доказать, что число 1111 + 1212 + 1313 делится на 10.
Решение:
Число 1111 оканчивается единицей. Выясним, какой цифрой оканчивается число 1212.
1 21 = …2
21 = …2
122 = …4
123 = …8
124 = …6
125 = …2
126 = …4
…
Отметим, что последняя цифра с возрастанием меняется периодически через 4 последовательных показателя. Т.к. 12 : 4 = 3 раза повторится период, то 1212 оканчивается цифрой 6. Теперь выясним, какой цифрой оканчивается число 1313
1 31 = …3
31 = …3
132 = …9
133 = …7
134 = …1
135 = …3
136 = …9
…
Аналогично рассуждая, получаем: 1313 оканчивается цифрой 3. Складываем последние цифры: 1 + 6 + 3 = 10, значит, число 1111 + 1212 + 1313 оканчивается нулем, следовательно, 1111 + 1212 + 1313 делится на 10.
Задача № 5
Доказать, что число 1015 + 1017 – 74 делится на 9.
Решение:
1015 + 1017 – 74 = 1015 – 115 + 1017 – 117 + 2 – 74 = (10 – 1) (…) + (10 – 1) (…) – 72 = 9 (…) +
+9 (…) – 9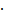 8 = 9(… + … – 8) – это число, очевидно, делится на 9.
8 = 9(… + … – 8) – это число, очевидно, делится на 9.
Задача № 6
Доказать, что при любом целом 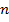 число
число 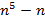 делится на 30.
делится на 30.
Решение:
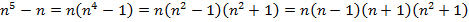 . Чтобы произведение делилось на 30, нужно, чтобы оно делилось на 5 и на 6.
. Чтобы произведение делилось на 30, нужно, чтобы оно делилось на 5 и на 6. 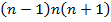 – произведение трех последовательных чисел, поэтому оно делится на
– произведение трех последовательных чисел, поэтому оно делится на 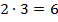 . Итак, чтобы доказать, что
. Итак, чтобы доказать, что 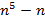 делится на 30, осталось доказать, что оно делится на 5.
делится на 30, осталось доказать, что оно делится на 5.
Если 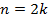 – четное, то его квадрат оканчивается на 4 или 6.
– четное, то его квадрат оканчивается на 4 или 6.
Если 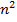 оканчивается на 4, то
оканчивается на 4, то 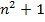 оканчивается на 5.
оканчивается на 5.
Если 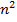 оканчивается на 6, то
оканчивается на 6, то 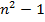 оканчивается на 5.
оканчивается на 5.
Если 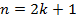 – нечетное, то
– нечетное, то 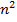 оканчивается на 1, или на 9, или на 5.
оканчивается на 1, или на 9, или на 5.
Если 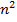 оканчивается на 9, то
оканчивается на 9, то 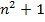 оканчивается на 0.
оканчивается на 0.
Если 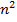 оканчивается на 1, то
оканчивается на 1, то 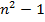 оканчивается на 0.
оканчивается на 0.
Если 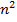 оканчивается на 5, то
оканчивается на 5, то 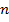 оканчивается на 5.
оканчивается на 5.
Значит, 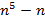 делится на 30.
делится на 30.
Задача № 7
Доказать, что при любом целом 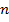 число
число 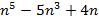 делится на 120.
делится на 120.
Решение:
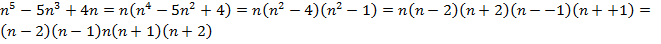 – произведение пяти последовательных чисел.
– произведение пяти последовательных чисел.
120 = 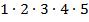 . Значит,
. Значит, 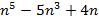 делится на
делится на 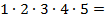 120.
120.
Задача № 8
Найти пятизначное число, если известно, что при умножении этого числа на 9 получается пятизначное число, записанное теми же цифрами, но в обратном порядке.
Решение:
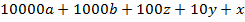 – данное пятизначное число.
– данное пятизначное число.
При умножении на 9 получим: 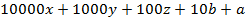 . Т.к. числа пятизначные, то
. Т.к. числа пятизначные, то 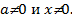 При умножении на 9 число остается пятизначным, поэтому
При умножении на 9 число остается пятизначным, поэтому 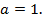 Тогда
Тогда 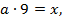 значит
значит 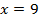 . После умножения на 9 получаем
. После умножения на 9 получаем
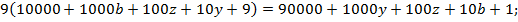
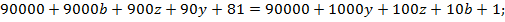
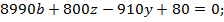
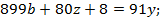
Т.к. 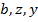 – однозначные числа, то даже если
– однозначные числа, то даже если 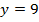 , то правая часть последнего равенства равна
, то правая часть последнего равенства равна 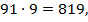 поэтому чтобы выполнялось равенство нужно взять
поэтому чтобы выполнялось равенство нужно взять 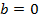 . Равенство примет вид:
. Равенство примет вид:
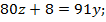
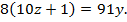
91 не делится на 8, поэтому 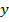 делится на 8, значит,
делится на 8, значит, 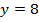 . Получаем:
. Получаем:
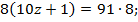
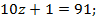
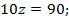
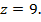
Т.о. 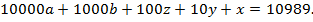
Задача № 9
Доказать, что если 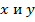 – целые числа такие, что число
– целые числа такие, что число 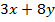 делится на 17, то число
делится на 17, то число 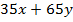 также делится на 17.
также делится на 17.
Решение:
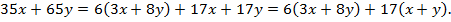
По условию 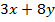 делится на 17, значит
делится на 17, значит 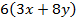 делится на 17.
делится на 17. 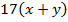 делится на 17 очевидно, следовательно,
делится на 17 очевидно, следовательно, 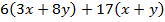 делится на 17, т.е. и
делится на 17, т.е. и 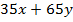 также делится на 17.
также делится на 17.
Задача № 10
Доказать, что сумма квадратов пяти последовательных целых чисел не является квадратом целого числа.
Решение:
Пусть 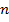 ,
, 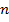 +1,
+1, 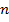 +2,
+2, 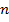 +3,
+3, 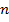 +4– пять последовательных целых чисел, тогда
+4– пять последовательных целых чисел, тогда
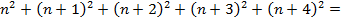
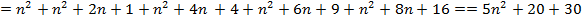
Дискриминант этого 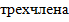 не равен 0, а значит, что 5
не равен 0, а значит, что 5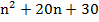 не равно квадрату какого–то целого числа.
не равно квадрату какого–то целого числа.
Задача № 11
Доказать, что если p 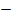 простое число, большее трех, то число
простое число, большее трех, то число 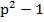 делится на 24.
делится на 24.
Решение:
Пусть p–простое число, 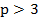 . Если
. Если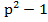 делится на 24, то
делится на 24, то 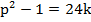 , где k
, где k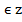 .
.
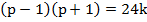
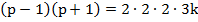
По условию р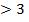 и p – простое число, поэтому р – нечетное. Тогда р
и p – простое число, поэтому р – нечетное. Тогда р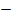 1 и р+1 – четные последовательные числа, значит, р
1 и р+1 – четные последовательные числа, значит, р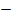 1 делится на 2, а р+1 делится на 4, т.е.
1 делится на 2, а р+1 делится на 4, т.е. 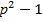 делится на 8. Так как р
делится на 8. Так как р 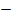 простое число , то оно не делится на 3, т.е. р=3k+1 или p=3k+2.
простое число , то оно не делится на 3, т.е. р=3k+1 или p=3k+2.
Если p=3k+1, то p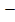 1=3k делится на 3 и тогда
1=3k делится на 3 и тогда 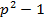 делится на 3
делится на 3  8=24
8=24
Если же p=3k+2, тогда p+1=3k+3 делится на 3 и тогда 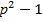 делится на 3
делится на 3 8=24 , что и требовалось доказать.
8=24 , что и требовалось доказать.
Задача № 12
Доказать, что если p 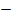 простое число и p
простое число и p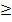 5, то остаток от деления числа
5, то остаток от деления числа 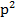 на 12 равен 1.
на 12 равен 1.
Решение:
По условию p – простое и p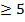 . Чтобы остаток от деления
. Чтобы остаток от деления 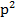 на 12 был равен 1, надо чтобы
на 12 был равен 1, надо чтобы 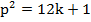 , где
, где 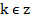 , т.е.
, т.е.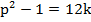 – таким образом надо доказать, что
– таким образом надо доказать, что 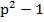 делится на 12.
делится на 12.
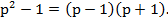 р – простое, не меньше чем 5,поэтому p – нечетное, тогда p – 1 и p + 1 четные последовательные числа, поэтому одно из них делится на 2, другое на 4. Осталось доказать, что
р – простое, не меньше чем 5,поэтому p – нечетное, тогда p – 1 и p + 1 четные последовательные числа, поэтому одно из них делится на 2, другое на 4. Осталось доказать, что 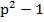 делится на 3.
делится на 3.
р – простое число, значит на 3 не делится, т.е. оно имеет вид p=3n+1 или p=3n+2, где n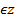 . Если p=3n+1, тогда p
. Если p=3n+1, тогда p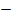 1=3n – делится на 3, значит и
1=3n – делится на 3, значит и 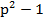 делится на 3.
делится на 3.
Если же p=3n+2, то p+1=3n+3 делится на 3. Это значит, что 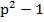 кратно 12:
кратно 12: 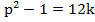 .
.
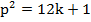 , т.е. остаток от деления
, т.е. остаток от деления 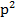 на 12 равен 1.
на 12 равен 1.
Задача № 13
Сколькими нулями оканчивается число, полученное при перемножении всех чисел от 1 до 100?
Решение:
Среди чисел от 1 до 100 содержится десять чисел, оканчивающихся нулями. Это 10, 20, 30, …, 90, 100. Произведение этих чисел оканчивается одиннадцатью нулями. Кроме того, среди чисел от 1 до 100 содержатся числа, оканчивающихся пятеркой 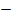 это 5, 15, 25, 35,…, 85, 95. Их десять. Каждое из этих чисел при умножении на четное число дает число, оканчивающееся нулем. Итак, еще 10 нулей. Кроме того, числа 25=5
это 5, 15, 25, 35,…, 85, 95. Их десять. Каждое из этих чисел при умножении на четное число дает число, оканчивающееся нулем. Итак, еще 10 нулей. Кроме того, числа 25=5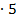 , 75=5
, 75=5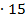 и 50=5
и 50=5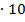 , имея в разложении еще по пятерке, при умножении на четное число дадут еще три числа, окачивающихся нулями. Значит, произведение всех чисел то 1 до 100 окачиваются 11+10+3=24 нулями.
, имея в разложении еще по пятерке, при умножении на четное число дадут еще три числа, окачивающихся нулями. Значит, произведение всех чисел то 1 до 100 окачиваются 11+10+3=24 нулями.
Задача № 14
Доказать, что если 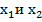 – корни квадратного уравнения
– корни квадратного уравнения 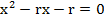 , где r
, где r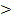 0, то выполняется неравенство
0, то выполняется неравенство 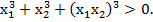
Решение:
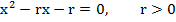
По теореме 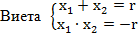
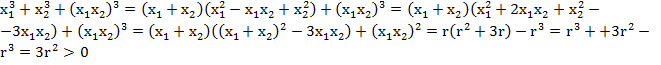 при r
при r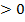 , что и требовалось доказать.
, что и требовалось доказать.
Задача № 15
Найти все значения r, для которых при действительных значениях x выполняется неравенство 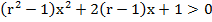
Решение:
Данное неравенство будет выполняться при всех действительных значениях х, если 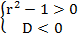
D=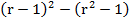
Решаем систему неравенств:
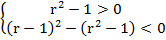
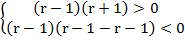
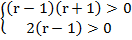
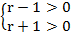
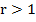 .
.
Если же r=1, неравенство принимает вид 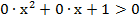 , т.е.
, т.е. 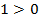 – верно.
– верно.
Ответ: 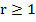
Задача № 16
Доказать, что при всех действительных значениях x справедливо неравенство:
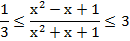
Решение:
Данное неравенство равносильно системе неравенств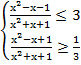
Так как 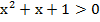 при любом x, то имеем:
при любом x, то имеем:
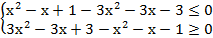
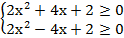
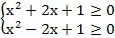
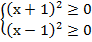
Оба неравенства справедливы при всех действительных значениях х. Значит, исходное неравенство справедливо при 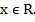
Задача № 17
Доказать неравенство 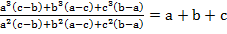
Решение:
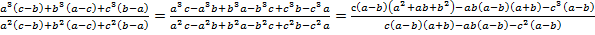 =
=
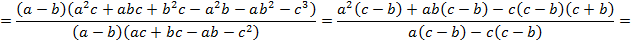
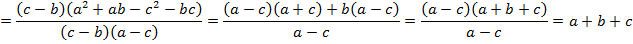
Задача № 18
Доказать неравенство 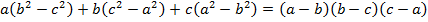
Решение:
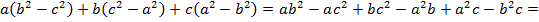
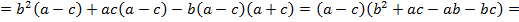
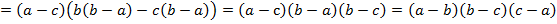
Задача № 19
Доказать равенство 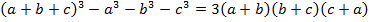
Решение:
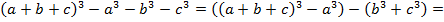
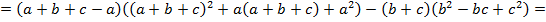
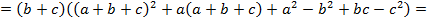
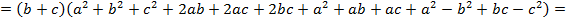
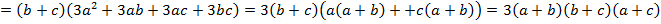
Задача № 20
Доказать равенство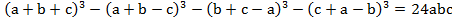
Решение:
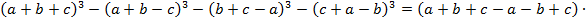
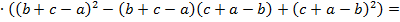
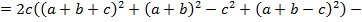
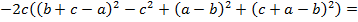
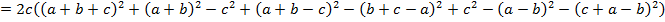
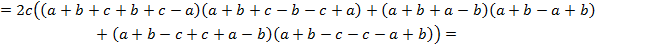
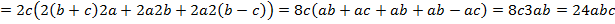
Нестандартные задачи в 1 классе
Тема урока: РЕШАЕМ ЗАДАЧИ (УМК –«Школа XXI века»).
Цели: учить отвечать на вопросы «на сколько больше….», «на сколько меньше…»; совершенствовать умение решать задачи; закреплять умение сравнивать.
Ход урока.
I. Устный счет.
1. Игра «Заселяем домики».
2. Задачи в стихах.
Пять грибочков под осинкой,
И под елкой тоже пять.
Помогите- ка Иринке
Все грибочки сосчитать! (5+5=10)
Мишка Вини рано встал,
Бочки с медом сосчитал.
Оказалось десять их,
Только что ж смотреть на них?
Три бочонка с медом съел,
Прогуляться захотел,
В полдень мишка наш пришел,
Сколько бочек он нашел?( 10-3=7)
II. Сообщение темы урока.
-Рассмотрите рисунки на доске.
-Какие вопросы можно задать по каждому рисунку? (Сколько всего? Сколько осталось?)
-Тема урока «Решаем задачи».
III. Изучение нового материала. Работа по учебнику.
1. Задание 1 (с.112) с использованием набора «Касса цифр».
-Сколько конфет на рисунке? (4.) Сколько орехов? (6)
-Как узнать, чего больше? Чего меньше? (Надо составить пары предметов. Больше орехов, меньше конфет).
Просмотр содержимого документа
«нестандартные задачи в 1 классе»


Инструкция
Для выполнения заданий вам необходимо выбрать инструмент, которым можно записывать ответы на вопросы. Для этого после запуска показа файлов щелкните правой кнопкой мыши в любом месте экрана для вызова контекстного меню и выберите Указатель в виде Карандаша или Ручки . Там же можно задать цвет чернил .
Для перехода со слайда на слайд используйте кнопки на экране или в контекстном меню (правая кнопка мыши) выберите команды Далее или Назад .
Желаем удачи!

Оля старше Вани, но моложе Коли. Кто из них старше всех?
Оля Ваня Коля

Оля Ваня Коля

Люба пришла домой раньше, чем Надя, а Надя – раньше, чем Саша. Кто из них пришёл домой последним?
Люба Надя Саша

Люба Надя Саша

В двух корзинах грибов было поровну. На суп взяли из одной корзины 7 грибов, а из другой — 5 грибов. В какой корзине грибов осталось больше и на сколько?
корзина

Во 2 корзине, на 2 гриба больше
В семье семь дочерей. Каждая из дочерей имеет одного брата. Сколько в этой семье мальчиков?
Ответ:
Ответ: 1
Миша нарисовал 4 картинки, а Саша – столько, полстолько и ещё одну. Сколько картинок нарисовал Саша?
Ответ:
Ответ: 4+2+1=7
В три чашки жёлтого, зелёного и синего цвета налили чай, молоко и сок. Какой напиток в каждой чашке, если чай не в синий и не в жёлтой чашке, а сок не в синей?
чай
сок
молоко