Олимпиада по математике кенгуру 2 класс ответы: Задачи прошлых лет | Конкурс Кенгуру – Кенгуру 2019 для 2 класса: задания, ответы, онлайн-тест

Олимпиадные задания по математике (2 класс) на тему: Подготовься к «Кенгуру»

Математическая олимпиада «Кенгуру»

Для каждой возрастной группы предлагаются задачи трёх уровней сложности:

Всего предлагется 30 задач, на решение отводится 75 минут. В ходе олимпиады запрещается пользоваться калькулятором и литературой.

Желаем успехов в решении!

Математическая олимпиада «Кенгуру» Подготовка.

Задача 5. Малыш, 3й уровень, 2006 год
Детская игрушка подвешена к потолку и находится в равновесии. Одинаковые фигурки весят одинаково. Шарик весит 30 граммов. Сколько весит кубик, отмеченный знаком вопроса?

А:10г; Б:20г; В:30г; Г:40г; Д:50г;

Задача 5.
Обратим внимание, что в формулировке задачи не говорится стандартная фраза «весом самой конструкции можно пренебречь». А ведь она и действительно не нужна – все перекладины уравновешивают друг друга и на решение не влияют.

Из правой части заметим, что трапеция равна по весу двум шарикам.
Из левой части одно сердечко равно по весу двум кубикам.
Значит, 6 кубиков равны четырём шарикам. 6 кубиков весят 120г, значит 1 кубик весит 20г. Ответ Б.

Задача 10. Малыш, 3й уровень, 2006 год
Ира, Аня, Катя, Оля и Эля живут в одном доме: две девочки на первом этаже и три на втором.. Оля живёт не на том этаже, где Катя и Эля. Аня — не на том этаже, где Ира и Катя. Кто живёт на первом этаже?
А:Катя и Эля; Б:Ира и Эля; В:Ира и Оля; Г:Ира и Катя; Д:Аня и Оля;

Задача 10.
Получается, что Ира и Катя, а также Катя и Эля живут на одном этаже. Значит, они живут на втором. На первом этаже тогда живут Аня и Оля.
Ответ Д:Аня и Оля;

Задача 15. Малыш, 3й уровень, 2003 год
В компании из пяти человек есть вруны, которые всегда говорят неправду, и честные, которые всегда говорят правду. Каждого из них спросили: «Сколько врунов в вашей компании?», на что были получены ответы: «один», «два», «три», «четыре» и «пять». Сколько на самом деле врунов в этой компании?
А:1; Б:2; В:3; Г:4; Д:5;

Задача 15.
Если бы честных в компании было несколько, то мы бы получили как минимум 2 одинаковых ответа (однако наличие одинаковых ответов не гарантирует того, что они принадлежат честным, ведь и вруны могли одинаково соврать). В нашем случае 5 врунов быть не может, поскольку тот, кто сказал “пять”, сказал бы правду. А вот 4 вруна – вполне возможно.
Ответ Г:4;

Задача 20. Малыш, 3й уровень, 2000 год
Красная Шапочка несла бабушке 14 пирожков: с мясом, грибами и капустой. Пирожков с капустой было больше всего, их было вдвое больше, чем пирожков с мясом, а пирожков с мясом было больше, чем пирожков с грибами. Сколько пирожков с грибами несла Красная Шапочка?
А:2; Б:4; В:5; Г:1; Д:3;

Задача 20.
Т.к. пирожков с капустой вдвое больше, чем с мясом, то их общее количество должно делиться на 3. Такое будет возможно только когда пирожков с грибами 2 или 5. Но если тех будет 5, то пирожков с мясом должно быть 4, что не соответствует второму условию. Значит. С грибами было всего 2 пирожка.
Ответ А:2

Задача 25. Малыш – 3,4, 3й уровень, 2008 г.
В коробке лежат 7 карточек с написанными на них числами от 1 до 7 (по одному числу на карточке). Первый мудрец наугад берёт три карточки из коробки, а второй – две (ещё две карточки остаются в коробке). Первый мудрец, глядя на свои карточки, говорит второму: «Я точно знаю, что сумма чисел  на твоих карточках чётная». Сумма чисел, записанных на карточках первого мудреца равняется:
А:6; Б:9; В:10; Г:12; Д:15;

Задача 26. Малыш – 2, 3й уровень, 2008 г.
Котик-Муркотик и Лисичка-Сестричка ловили рыбу. К ним подбежал голодный Волчик-Братик и спросил, много ли рыбы они поймали? Лисичка хитро ответила: у нас двоих рыб на 7 больше, чем у меня одной, а у одного из нас на 17 рыб меньше, чем у другого. Сколько рыбы словили вместе Котик-Муркотик и Лисичка-Сестричка?
А:10; Б:17; В:22; Г:27; Д:31;

Задача 25.
Первый мудрец  будет точно знать, что сумма цифр на карточках сторого мудреца чётна лишь в том случае, если ему будет известно, что все оставшиеся числа – одной чётности. Следовательно, ему могли выпасть только карточки с числами 2, 4 и 6, их сумма равна 12. Данная задача проходила в 2008 году сквозь все классы и была использована для мониторинга умения совершать логические умозаключения. Наряду со стабильным ростом из класса в класс, тем не менее был отмечен общий низкий уровень данного умения.
Ответ: Г:12

Задача 26.
Если у них двоих рыб на 7 больше, чем у Лисички, то эти 7 рыб принадлежат Коту. И выходит, что у Лисички рыб на 17 больше, т.е. 24. Итого 31 рыба.
Ответ: Д:31

Задача 31. Малыш, 3й уровень, 2002 год
На счётчике пробега моей машины сейчас показано число 187369 (км). В этом числе все цифры различны. Какое наименьшее количество километров нужно проехать, чтобы на счётчике опять появилось число, у которого все цифры различны?
А:1; Б:21; В:431; Г:12431; Д:13776

Задача 31.
Эта задача – хороший пример приёма перебора в тесте. Вместо того, чтобы непосредственно вычислять, какое расстояние нужно проехать, прежде чем вновь появится число из разных цифр, будет последовательно пытаться прибавлять к 187369 числа из вариантов ответа и смотреть, что получится.
187369+1=187370 – не подходит
187369+21=187390 – подошло!
Ответ Б:21;

Задача 36. Малыш, 3й уровень, 2000 год
Если мы умножим число 12345679 на 9, то получим число 111111111. Если мы умножим его на 18, то получим результат, который содержит только цифры 2. Если мы умножим это число на 27, то получим число, которое записывается только при помощи цифры 3. На какое число нужно умножить число 12345679, чтобы получить число из одних семёрок?
А:43; Б:53; В:63; Г:73; Д:83;

Задача 36.
Чтобы получить число из одних семёрок, нужно умножить 111111111 на 7, а это то же самое, если умножить 12345679 на 9*7=63. Кстати, на свойствах 12345679, “числа без восьмёрки”, основано ещё несколько интересных математических трюков и фокусов. А чтобы понять, что в нём такого особенного, разделите 1 на 81.
Ответ В:63;

Задача 36. Малыш, 3й уровень, 2000 год
Если мы умножим число 12345679 на 9, то получим число 111111111. Если мы умножим его на 18, то получим результат, который содержит только цифры 2. Если мы умножим это число на 27, то получим число, которое записывается только при помощи цифры 3. На какое число нужно умножить число 12345679, чтобы получить число из одних семёрок?
А:43; Б:53; В:63; Г:73; Д:83;

Задача 36.
Чтобы получить число из одних семёрок, нужно умножить 111111111 на 7, а это то же самое, если умножить 12345679 на 9*7=63. Кстати, на свойствах 12345679, “числа без восьмёрки”, основано ещё несколько интересных математических трюков и фокусов. А чтобы понять, что в нём такого особенного, разделите 1 на 81.
Ответ В:63;

Задача 41. Малыш, 3й уровень, 2005
Марк загадал трёхзначное и двузначное числа, разность которых равна 989. Тогда сумма этих чисел равна:
А: 1000;Б: 1001; В: 1009; Г: 1010; Д: 2005;

Задача 41
Число 989 может получиться только если от наибольшего трёхзначного отнять наименьшее двузначное число: 989=999-10.  Значит, сумма этих чисел равна 999+10=1009.
Ответ В: 1009

Задача 46. Малыш – 3,4, 3й уровень, 2009
Маша коллекционирует фотографии известных спортсменов. Количество фотографий, которые она собирает за каждый год равно количеству фото, собранных за два предыдущих года. В 2008 году она собрала 60 фотографий, а в этом – 69. Сколько фотографий собрала Маша в 2006 году?
 А: 20;Б: 24; В: 36; Г: 40; Д: 48;

Задача 47. Малыш – 2, 3й уровень, 2009
Серёжа подбрасывал игральный кубик четыре раза и каждый раз записывал полученное число очков. Сложив эти числа, он получил 21 очко. Какое наибольшее количество раз могла выпадать тройка?
А: 0;Б: 1; В: 2; Г: 3; Д: 4;

Задача 46 
В 2007 Маша должна была собрать 36 фотографий, чтобы в сумме с 60 фото, собранными в 2008 году получилось 96 фотографий 2009 года. А в 2006 было собрано 60-36=24 фотографии. Обратите внимание, как тонко здесь для задачи 3-4 классов вводятся свойства последовательности Фибоначчи.
Ответ Б: 24 

Задача 47 
Какую наибольшую сумму очков мог получить Серёжа? 6*4=24. Полученная им сумма в 21 всего на 3 очка меньше максимальной. А замена шестёрки тройкой также уменьшает максимальную сумму на 3. Поэтому тройка могла выпасть всего раз.
Ответ Б: 1 

Задача 52. Малыш, 3й уровень, 2001 год
В обувном магазине для животных на 10 полках было по 12 пар обуви. Первыми покупателями были пять многоножек. Первые три из них купили по 30 пар, а две следующие – по 5 пар каждая. Сколько пар обуви осталось в магазине после визита этих покупателей?
А:10; Б:15; В:20; Г:25; Д:30;

Задача 52.
Решим задачу по вопросам
Вопрос 1. Сколько пар обуви было в магазине сначала?
10×12=120 (пар)

Вопрос 2. Сколько пар обуви купили первые три многоножки?
3×30=90 (пар)

Вопрос 3. Сколько пар обуви купили первые три многоножки?
2×5=10 (пар)

Вопрос 4. Сколько пар обуви было куплено всего?
10+90=100 (пар)

Вопрос 5. Сколько пар обуви осталось в магазине?
120-100=20 (пар)
Ответ В:20;

Задача 57. Малыш, 3й уровень, 2006 год
Между числами 2002 ? 2003 ? 2004 ? 2005 ? 2006 вместо каждого знака вопроса можно записать знак + или -. Какое из чисел не может получиться?
А:1988; Б:2001; В:2002; Г:2004; Д:2006;

Задача 57.
Поскольку в полученном выражении будет два нечётных числа, независимо от расстановки знаков, его значение будет чётным. Значит, не может получиться число 2001.
Ответ Б:2001;

Задача 62. Малыш, 3й уровень, 2002 год
В соревнованиях по бегу участвовали 28 детей. Количество детей, которые прибежали позже Димы вдвое больше количества детей, которые прибежали раньше Димы. В таком случае Дима прибежал:
А: шестым; Б: седьмым; В: восьмым; Г: девятым; Д: десятым

Задача 62.
Остальных участников забега было 27. Если разделить 27 в отношении 1:2, получим 9 и 18. Значит, 9 участников финишировали раньше Димы. Выходит, он пришёл десятым.
Ответ Д: десятым;

Задача 67. Малыш, 3й уровень, 2002 год
Рассмотрим число 12321232123212321…, состоящее из 2002 цифр. Тремя последними цифрами этого числа будут:
А: 123; Б: 232; В: 321; Г: 212; Д: 321;

Задача 67.
Можно заметить, что в заданном числе будет повторяться группа цифра 1232. Т.к. общее количество цифр, 2002, даёт остаток 2 при делении на 4, то число будет оканчиваться на …123212 и последними тремя цифрами будут 212.
Ответ Г: 212;

Задача 72. Малыш, 3й уровень, 2002 год
В каждом подъезде на каждом этаже 16-этажного дома есть по 4 квартиры. В каком подъезде и на каком этаже находится квартира №165?
А: 3 подъезд 9 этаж; Б: 3 подъезд 10 этаж; В: 3 подъезд 12 этаж; Г: 2 подъезд 13 этаж; Д: 3 подъезд 7 этаж;

Задача 72.
В одном подъезде 64 квартиры. Т.к. 165=2*64+9*4+1, то квартира 165 будет в (2+1=3) третьем подъезде на (9+1=10) десятом этаже.
Ответ Б: 3 подъезд 10 этаж;

Задача 77. Малыш, 3й уровень, 2001 год
Маленький Мук и королевский скороход соревновались в беге на дорожке длиной 30 км, которая проходила вокруг большого луга. По условиям состязания, выиграет тот, кто обгонит другого, пробежав на один круг больше. Скороход пробегает круг за 10 минут, а Маленький Мук – за 6 минут. Оба стартуют одновременно из одного и того же места. Через сколько минут Маленький Мук победит?
А: 5; Б: 10; В: 15; Г: 20; Д: 25;

Задача 77.
Сколько километров пробегает скороход за минуту?
30/10 = 3 (км)

Сколько километров пробегает Маленький Мук за минуту?
30/6 = 5 (км)

На сколько километров обгоняет Маленький Мук обгоняет скорохода каждую минуту?
5 – 3 = 2 (км).

Через сколько минут Маленький Мук обгонит скорохода на 30 км?

30/2 = 15 (мин)
Ответ В: 15;

Задача 82. Малыш, 3й уровень, 2001 год
В футбольном матче победитель получает 3 очка, проигравший – 0, а ничья оценивается одним очком. После 31 матча моя любимая команда имела 64 очка, причём 7 матчей она сыграла вничью. Сколько раз проиграла моя любимая команда?
А: 0; Б: 5; В: 19; Г: 21; Д: 24;

Задача 82.
За победы команда получила 64-7=57 очков.
Значит, побед было 57/3=19.
Т.к. из 31 матча было 7 ничьих и 19 побед, то поражений было 31-7-19=5.
Ответ Б: 5;

Задача 87. Малыш-3,4 классы, 3й уровень, 2009 год
На клумбе расцвели цветы: белый, красный, синий и жёлтый. Пчела Майя подлетает к каждом цветку всего 1 раз. Сначала она летит к красному цветку, а затем – к остальным. Майя не может лететь с жёлтого цветка сразу на белый. Сколькими способами пчела Майя может посетить все 4 цветка?
А: 1; Б: 2; В: 3; Г: 4; Д: 6;

Задача 88. Малыш-2 класс, 3й уровень, 2008 год
Петя прибавляет 2, Назар отнимает 1, а Дима удваивает число. Каждый мальчик выполняет своё действие только один раз. В каком порядке им нужно выполнять эти действия, чтобы из 3 получить 9?
А: Дима, Петя, Назар;
Б: Петя, Дима, Назар;
В: Дима, Назар, Петя;
Г: Назар, Дима, Петя;
Д: Петя, Назар, Дима;

Задача 87.
Первый цветок она выбирает однозначно. Второй цветок может быть выбран одним из трёх способов:
Красный-Белый,
Красный -Синий или
Красный -Жёлтый.
Поскольку с жёлтого цветка нельзя лететь сразу на белый, получаем 5 способов для трёх цветков:
Красный — Белый — Жёлтый,
Красный — Белый — Синий,
Красный — Синий — Белый,
Красный — Синий — Жёлтый,
Красный — Жёлтый — Синий
Но среди этих способов один путь, а именно, Красный — Синий — Жёлтый – тупиковый, т.к. никакой цветок, кроме белого, не остаётся, а на него лететь нельзя. Остальные же 4 тройки дают нам 4 возможных маршрута облёта цветов:
Красный – Белый – Жёлтый – Синий,
Красный – Белый – Синий – Жёлтый,
Красный – Синий – Белый– Жёлтый,
Красный – Жёлтый – Синий– Белый
Ответ Г: 4;

Задача 88.
Поскольку 9=(3+2)*2-1, то сначала посчитать должен Петя, затем Дима, и потом — Назар;
Б: Петя, Дима, Назар;

Задача 93. Малыш-3,4 классы, 3й уровень, 2009 год
Сколько существует двузначных чисел, у которых цифра справа больше цифры слева?
А: 9; Б: 18; В: 26; Г: 30; Д: 36;

Задача 94. Малыш-2 класс, 3й уровень, 2009 год
Секретный агент хочет расшифровать код из шести цифр. Он знает, что сумма цифр на первом, третьем и пятом местах равна сумме цифр на втором, четвёртом и шестом местах. Какой из предложенных вариантов не может быть кодом?
А: 81**61;
Б: 7*727*;
В: 4*4141;
Г: 12*9*8;
Д: 181*2*;

Задача 93.
Среди чисел, которые начинаются на 1, таких чисел будет 8: от 12 до 19. среди начинающихся на 2 их будет 7: от 23 до 29. И т.д., для начинающихся на 8 будет всего одно число – 89, а для следующего десятка таких не будет сосем. Ответом будет сумма 8+7+6+5+4+3+2+1=4х9=36
Ответ Д: 36;

Задача 94.
Рассмотрим для каждого из вариантов, может ли выполниться условие:
А: 81**61;
8+*+6=1+*+1
14+*=2+*
12+*=*
На местах звёздочек должны стоять цифры, различающиеся на 12, что невозможно.

Б: 7*727*;
7+7+7=*+2+*
19=*+*
Две цифры не могут дать в сумме 19

В: 4*4141;
4+4+4=*+1+1
10=*
Невозможно

Г: 12*9*8;
1+*+*=2+9+8
*+*=18
А вот это возможно, т.к. 9+9=18 и кодом будет последовательность 129998

Д: 181*2*;
1+1+2=8+*+*
Здесь правая часть уже явно больше левой.

Так что единственный вариант ответа, который может быть кодом — это 12*9*8;

Ответ Г: 12*9*8;

Задача 99. Малыш-3,4 классы, 3й уровень, 2008 год
Есть 5 коробок с карточками с буквами B, R, A, V, O.
В первой лежат B, V
Во второй лежат B, A, V, R
В третьей лежат A, B
В четвёртой лежит V
В пятой лежат B, R, A, V, O

Петя вытащил из коробок карточки так, чтобы в каждой коробке осталось по одной карточке и в разных коробках остались карточки с разными буквами. Какая буква останется во второй коробке?

А: B; Б: R; В: A; Г: V; Д: O;

Задача 100. Малыш-2 класс, 3й уровень, 2008 год
Маша подарила маме, бабушке, тёте и двум сёстрам по букету цветов. Цветы для сестёр и тёти были одного цвета. Известно, что бабушке она подарила не розы. Какой из этих букетов получила мама?

А: Жёлтые тюльпаны; Б: Розовые розы; В: Красные гвоздики; Г: Жёлтые розы; Д: Жёлтые гвоздики;

Задача 99.
Из четвёртой коробки ничего не нужно вытаскивать. Там останется V.
Значит, из первой нужно вытащить V и оставить В.
Тогда из третьей нужно вытащить В и оставить А.
И из второй нужно вытащить B, A, V и оставить R
Из пятой тогда Петя вытащит всё, кроме О.

Ответ Б: R;

Задача 100.
Три жёлтых букета: А, Г и Д получили тётя и сёстры. Т.к. бабушка получила не розы, то она получила гвоздики, а маме Маша подарила розовые розы.

Ответ Б: Розовые розы;

Задачи олимпиады Кенгуру, решения и ответы

С 1997 по 2012 годы, за пятнадцать лет проведения в Украине олимпиады Кенгуру, собралась обширная база нестандартных математических задач. Они печатаются в ежегодном вестнике олимпиады, кроме того, к юбилею конкурса вышел сборник «10 років разом. Міжнародний математичний конкурс «Кенгуру»», в котором собраны условия всех задач за 1997-2006 годы.

Решение таких задач — хороший интеллектуальный досуг, вне зависимости от возраста. Помимо этого, в свете современных образовательных требований, решение задач Кенгуру может оказаться отличным подспорьем в подготовке к Независимому внешнему оцениванию.

Здесь мы представляем свои варианты решения интересных на наш взгляд задач. Раздел регулярно пополняется. В пакет задач входит по одной задачи для каждого возраста, как правило, наивысшего (третьего) уровня сложности.

Краткие правила олимпиады

Участники олимпиады в зависимости от возраста делятся на следующие группы:

C 2007 года были введены уровни «Малюк 2»: 2 класс и «Випускник»: все 11-е классы.

Для каждой возрастной группы предлагаются задачи трёх уровней сложности:

Всего предлагется 30 задач, на решение отводится 75 минут. В ходе олимпиады запрещается пользоваться калькулятором и литературой.

Желаем успехов в решении!

Задачи на сайте формируются в виде пакетов. В каждый пакет входит по одной задаче каждого возрастного уровня. Уровень сложности, как правило, третий.

• Пакет 1: комбинаторика, логика, взвешивания
• Пакет 2: комбинаторика, логика, выражения
• Пакет 3: взвешивания, логика, делимость
• Пакет 4 : делимость, последовательности, рассуждения
• Пакет 5: вероятность, геометрия, логика
• Пакет 6: целая и дробная часть, делимость, цифры
• Пакет 7: комбинаторика, среднее арифметическое, дроби
• Пакет 8: числовые процессы, выбор, множества
• Пакет 9: комбинаторика, проценты, ребус
• Пакет 10: целые числа, уравнения, логика
• Пакет 11: целые числа, делимость, палиндромы
• Пакет 12: последовательности, проценты, уравнения
• Пакет 13: принцип Дирихле, цифры, множества
• Пакет 14: комбинаторика, делимость, геометрия
• Пакет 15: системы счисления, геометрия, арифметика
• Пакет 16: целые числа, логика, геометрия
• Пакет 17: тригонометрия, неравенства, геометрия
• Пакет 18: тригонометрия, последовательность, цифры
• Пакет 19: тригонометрия, последовательность, цифры

Далее>

Задайте вопрос на блоге о математике

Кенгуру 2017 для 3 — 4 класса

На рисунке справа изображены бусы. На каком рисунке изображены те же бусы?

Правильно!

Неправильно!

—

На рисунке изображены три квадрата, разбитых на клетки. На крайних квадратах часть клеток закрашена, а остальные — прозрачные. Оба эти квадрата наложили на средний квадрат так, что их верхние левые углы совпали. Какая их фигурок осталась видна?

Правильно!

Неправильно!

—

Спереди дом выглядит так, как изображено на рисунке. Сзади у этого дома есть дверь и два окна. Как он выглядит сзади?

Правильно!

Неправильно!

—

Миша сложил квадратный лист бумаги и проткнул в нём дырку. Потом он развернул лист и увидел то, что изображено на рисунке справа. Как могли выглядеть линии сгиба?

Правильно!

Неправильно!

—

Из прямоугольника 4 * 3 Федя вырезал две одинаковые фигурки. Какого вида фигурки у него не могли получиться?

Правильно!

Неправильно!

—

Стопка карточек с дырками нанизана на нитку (см. рисунок). Каждая карточка с одно стороны белая, а с другой — закрашенная. Вася разложил карточки на столе. Что у него могло получиться?

Правильно!

Неправильно!

—

Урок-презентация «Кенгуру — 2013» 2 класс

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

2 слайд

Описание слайда:

Задачи, оцениваемые в 3 балла

3 слайд

Описание слайда:

Два кузнечика прыгают по буквам слова КЕНГУРУ. Они начали с крайних букв и прыгают одновременно навстречу друг другу. При каждом прыжке кузнечики перепрыгивают на соседнюю букву. На какой букве они встретятся? (A) К (Б) Е (В) Н (Г) Г (Д) У К Н Р У Г У Е

4 слайд

Описание слайда:

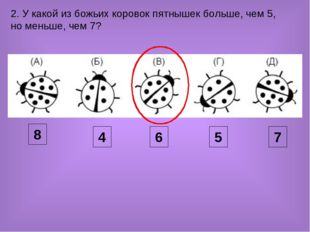
2. У какой из божьих коровок пятнышек больше, чем 5, но меньше, чем 7? 8 4 6 5 7

5 слайд

Описание слайда:

3. В зоопарке родились три львенка и четыре орленка. Сколько лап добавилось при этом в зоопарке? (A) 36 (Г) 24 (Б) 32 (В) 28 (Д) 20 4 + 4 + 4 + 2 + 2 + 2 + 2 = 20

6 слайд

Описание слайда:

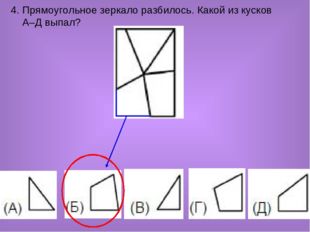
4. Прямоугольное зеркало разбилось. Какой из кусков А–Д выпал?

7 слайд

Описание слайда:

5. Что получится, если к удвоенной тройке прибавить утроенную двойку? (A) 5 (Б) 6 (В) 10 (Г) 12 (Д) 15 3 · 2 2 · 3 + = 6 12 6

8 слайд

Описание слайда:

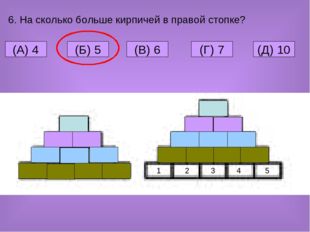
6. На сколько больше кирпичей в правой стопке? (A) 4 (Б) 5 (В) 6 (Г) 7 (Д) 10 1 2 3 4 5

9 слайд

Описание слайда:

7. Каких карточек на рисунке больше всего? 6 5 5 5

10 слайд

Описание слайда:

8. На следующий день после дня рождения Петя сказал: «Послезавтра будет среда». Когда у Пети был день рождения? (A) в понедельник (Б) во вторник (В) в пятницу (Г) в субботу (Д) в воскресенье

11 слайд

Описание слайда:

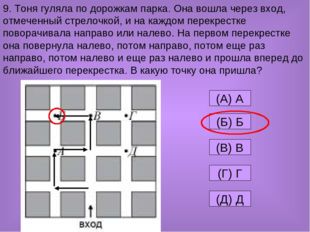
9. Тоня гуляла по дорожкам парка. Она вошла через вход, отмеченный стрелочкой, и на каждом перекрестке поворачивала направо или налево. На первом перекрестке она повернула налево, потом направо, потом еще раз направо, потом налево и еще раз налево и прошла вперед до ближайшего перекрестка. В какую точку она пришла? (A) А (Б) Б (В) В (Г) Г (Д) Д

12 слайд

Описание слайда:

10. Урок во втором классе длится 40 минут, а перемена — 10 минут. Сколько минут проходит от середины первого урока до середины второго? (A) 20 (Д) 55 (Г) 50 (В) 40 (Б) 30 40 мин. 10 мин. 40 мин. 40 : 2 = 20 40 : 2 = 20 20 + 10 + 20 = 50 мин.

13 слайд

Описание слайда:

Задачи, оцениваемые в 4 балла

14 слайд

Описание слайда:

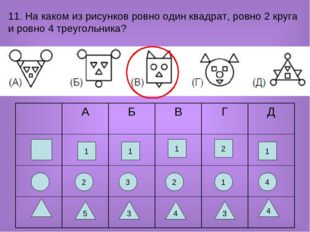
11. На каком из рисунков ровно один квадрат, ровно 2 круга и ровно 4 треугольника? 1 1 1 2 1 2 4 1 2 3 5 4 3 4 3

15 слайд

Описание слайда:

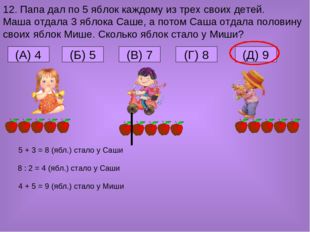
12. Папа дал по 5 яблок каждому из трех своих детей. Маша отдала 3 яблока Саше, а потом Саша отдала половину своих яблок Мише. Сколько яблок стало у Миши? (A) 4 (Д) 9 (Г) 8 (В) 7 (Б) 5 5 + 3 = 8 (ябл.) стало у Саши 8 : 2 = 4 (ябл.) стало у Саши 4 + 5 = 9 (ябл.) стало у Миши

16 слайд

Описание слайда:

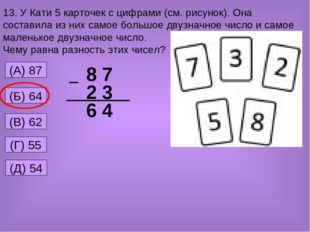
13. У Кати 5 карточек с цифрами (см. рисунок). Она составила из них самое большое двузначное число и самое маленькое двузначное число. Чему равна разность этих чисел? (A) 87 (Б) 64 (В) 62 (Г) 55 (Д) 54 8 7 2 3 6 4

17 слайд

Описание слайда:

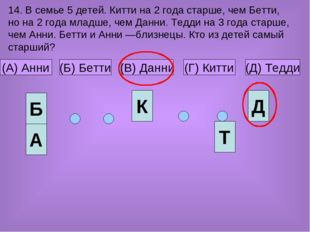
14. В семье 5 детей. Китти на 2 года старше, чем Бетти, но на 2 года младше, чем Данни. Тедди на 3 года старше, чем Анни. Бетти и Анни —близнецы. Кто из детей самый старший? (A) Анни (Б) Бетти (В) Данни (Г) Китти (Д) Тедди К Б А Д Т

18 слайд

Описание слайда:

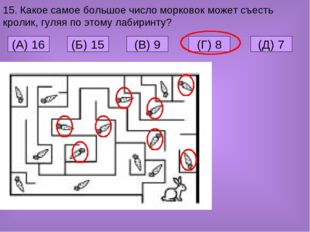
15. Какое самое большое число морковок может съесть кролик, гуляя по этому лабиринту? (A) 16 (Г) 8 (Б) 15 (В) 9 (Д) 7

19 слайд

Описание слайда:

16. Каждый раз, когда Буратино врет, его нос удлиняется на 6 см, а если он говорит правду — укорачивается на 2 см. Вчера за день его нос менял длину 5 раз, и в итоге удлинился на 6 см. Сколько раз за этот день Буратино соврал? (A) 1 (Б) 2 (Г) 4 (В) 3 (Д) 5 врёт + 6 см говорит правду — 2 см = 6 см 6 + 6 – 2 – 2 – 2 = 6 6– 2 + 6 – 2 – 2 = 6 6– 2 – 2 + 6 – 2 = 6 6– 2 – 2 – 2 + 6 = 6

20 слайд

Описание слайда:

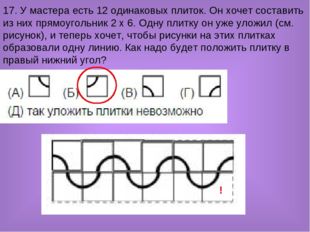
17. У мастера есть 12 одинаковых плиток. Он хочет составить из них прямоугольник 2 x 6. Одну плитку он уже уложил (см. рисунок), и теперь хочет, чтобы рисунки на этих плитках образовали одну линию. Как надо будет положить плитку в правый нижний угол? ? !

21 слайд

Описание слайда:

18. В числе 2013 сумма первых трех цифр равна четвертой. Сколько чисел от 2014 до 2100 обладают таким же свойством? (A) 9 (Д) 5 (Г) 6 (В) 7 (Б) 8 2013 2+0+1=3 2+0+2=4 2+0+3=5 2+0+4=6 2+0+5=7 2+0+6=8 2+1+0=3 2103 2+0+7=9 1 2 3 4 5 6

22 слайд

Описание слайда:

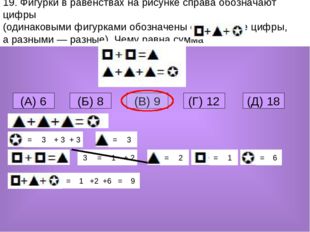
19. Фигурки в равенствах на рисунке справа обозначают цифры (одинаковыми фигурками обозначены одинаковые цифры, а разными — разные). Чему равна сумма (A) 6 (Б) 8 (В) 9 (Г) 12 (Д) 18 = 3 + 3 + 3 3 = = 3 + 2 1 = 2 = 1 = 6 = +6 +2 1 = 9

23 слайд

Описание слайда:

20. В магазине «Все для магии» ничего не продают, но меняют одни волшебные предметы на другие. Ковер-самолет можно поменять на две шапки-невидимки, а шапку-невидимку можно получить три волшебных дудочки, а две волшебных дудочки можно обменять на волшебную палочку. На сколько волшебных палочек можно обменять два ковра-самолета? (A) 20 (Б) 12 (В) 8 (Г) 6 (Д) 4 1 ковёр = 2 шапкам 1 шапка = 3 дудочкам 2 дудочки = 1 волш. палочке 2 ковра = 2 · 2 = 4 шапкам 4 шапки = 3 · 4 = 12 дудочек 12 дудочек : 2 = 6 волш. палочек 2 КОВРА= ? ВОЛШ. ПАЛОЧЕК

24 слайд

Описание слайда:

Задачи, оцениваемые в 5 балла

25 слайд

Описание слайда:

21. У Анны есть одна монета в 5 центов, одна монета в 10 центов, одна монета в 20 центов и одна монета в 50 центов. Сколько разных сумм она сможет заплатить без сдачи? (A) 5 (Б) 7 (В) 8 (Г) 12 (Д) 15 10 5 20 10 5 10 5 5 20 10 20 50 10 50 20 50 5 50 5 5 5 10 10 20 50 10 20 50 50 20 20 50 1 2 3 4 5 6 7 8 9 10 11 12 14 13 15

26 слайд

Описание слайда:

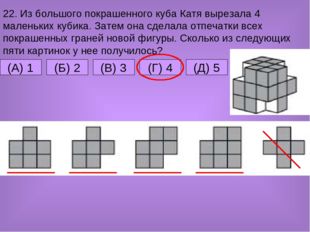
22. Из большого покрашенного куба Катя вырезала 4 маленьких кубика. Затем она сделала отпечатки всех покрашенных граней новой фигуры. Сколько из следующих пяти картинок у нее получилось? (A) 1 (Б) 2 (В) 3 (Д) 5 (Г) 4

27 слайд

Описание слайда:

23. Квадратную коробку заполнили в два слоя одинаковыми квадратными шоколадками. Кирилл съел все 20 шоколадок верхнего слоя, которые лежали вдоль стенок коробки. Сколько шоколадок осталось в коробке? (A) 16 (Б) 30 (В) 50 (Г) 52 (Д) 72 1 2 3 21 20 28 6 5 4 27 26 25 19 7 24 23 22 34 31 16 33 30 17 29 18 8 14 10 36 35 9 32 15 11 12 13 36 + 36 = 72 всего 72 — 20 = 52 осталось

28 слайд

Описание слайда:

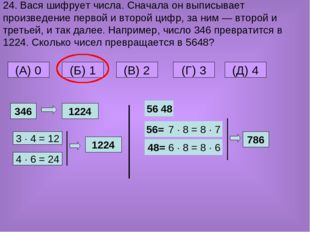
24. Вася шифрует числа. Сначала он выписывает произведение первой и второй цифр, за ним — второй и третьей, и так далее. Например, число 346 превратится в 1224. Сколько чисел превращается в 5648? (A) 0 (Б) 1 (В) 2 (Г) 3 (Д) 4 346 1224 3 · 4 = 12 4 · 6 = 24 1224 56 48 56= 48= 7 · 8 = 8 · 7 6 · 8 = 8 · 6 786

29 слайд

Описание слайда:

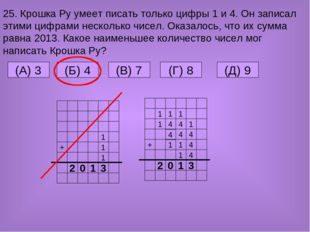
25. Крошка Ру умеет писать только цифры 1 и 4. Он записал этими цифрами несколько чисел. Оказалось, что их сумма равна 2013. Какое наименьшее количество чисел мог написать Крошка Ру? (A) 3 (Б) 4 (В) 7 (Д) 9 (Г) 8 + 1 2 1 1 0 1 3 + 2 1 0 3 1 1 4 1 4 4 1 4 4 1 4 1 4 1 1

30 слайд

Описание слайда:

Презентация составлена учителем начальных классов МАОУ «Лицей №11№» г. Великие Луки Долгашевой Еленой Николаевной.

Курс профессиональной переподготовки

Учитель математики

Курс повышения квалификации

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс:
Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник:
Все учебники

Выберите тему:
Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала:

ДБ-165098

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий