Олимпиадные задания по математике (4 класс) на тему: материалы для подготовки к олимпиаде по математике для 4 класса №1
Олимпиадные задания по математике
1. Не меняя расположения цифр, поставьте между ними знак сложения таким образом, чтобы получилась сумма равная 100. Если понадобится, две любые стоящие рядом цифры считайте двузначным числом. Выполните задание двумя разными способами.
2. Напишите цифрами число, состоящее из 22 миллионов 22 тысяч 22 сотен и 22 единиц.
3. Какие четыре цифры надо вычеркнуть из числа 4921508, чтобы получившееся трёхзначное число было как можно меньше?
4. У царя Гороха 7 сыновей, у каждого его сына по 7 сыновей, а у каждого внука царя Гороха по две дочери. Сколько правнучек у царя Гороха?
5. Шестеро тянут репку: дедка вдвое сильнее бабки, бабка вдвое сильнее внучки, внучка вдвое сильнее Жучки, Жучка вдвое сильнее кошки, кошка вдвое сильнее мышки. Сколько нужно позвать мышек, чтобы они сами вытянули репку?
6. От пристани одновременно в одном направлении отчалили пароход и катер со скоростями соответственно 24 км/ч и 15 км/ч. Через 4 часа пароход сел на мель. Снявшись через некоторое время с мели, он догнал катер через час. Сколько времени простоял пароход на мели?
7. Три команды набрали на олимпиаде 285 баллов. Если бы команда школы №24 набрала на 8 баллов меньше, а команда школы №44 на 12 баллов меньше, команда школы №77 на 7 баллов меньше, то все они набрали бы поровну баллов. Сколько баллов набрали команды школ №24 и №77 вместе?
8. Если сторону квадрата, периметр которого 36 см, уменьшить в 3 раза, то получится ширина прямоугольника, периметр которого 22 см. Найдите длину этого прямоугольника и вычислите площадь.
9. Рысь съедает 600 кг мяса за 6 часов, а тигр в 2 раза быстрее. За какое время они съедят это мясо вместе?
10. 5 землекопов за 5 часов выкапывают 5 метров канавы. Сколько землекопов смогут за 100 часов выкопать 100 метров канавы?
Ответы на олимпиадные задания
1. Не меняя расположения цифр, поставьте между ними знак сложения таким образом, чтобы получилась сумма равная 100. Если понадобится, две любые стоящие рядом цифры считайте двузначным числом. Выполните задание двумя разными способами.
1 + 2 + 34 + 56 + 7 = 100
1 + 23 + 4 + 5 + 67 = 100
2. Напишите цифрами число, состоящее из 22 миллионов 22 тысяч 22 сотен и 22 единиц.
22 024 222
3. Какие четыре цифры надо вычеркнуть из числа 4921508, чтобы получившееся трёхзначное число было как можно меньше?
1 балл
вычеркнуть цифры 4,9,2,5.
число: 108
4. У царя Гороха 7 сыновей, у каждого его сына по 7 сыновей, а у каждого внука царя Гороха по две дочери. Сколько правнучек у царя Гороха?
1) 7*7=49 (внуков)
2) 49*2= 98(правнучек)
3 балла
5. Шестеро тянут репку: дедка вдвое сильнее бабки, бабка вдвое сильнее внучки, внучка вдвое сильнее Жучки, Жучка вдвое сильнее кошки, кошка вдвое сильнее мышки. Сколько нужно позвать мышек, чтобы они сами вытянули репку?
Сила кошки = силе 2 мышек
Сила Жучки = силе 4 мышек (2*2)
Сила внучки = силе 8 мышек (4*2)
Сила бабки = силе 16 мышек (8*2)
Сила дедки = силе 32 мышек (16*2)
1+2+4+8+16+32= 63 мышки
4 балла
6. От пристани одновременно в одном направлении отчалили пароход и катер со скоростями соответственно 24 км/ч и 15 км/ч. Через 4 часа пароход сел на мель. Снявшись через некоторое время с мели, он догнал катер через час. Сколько времени простоял пароход на мели?
1) 4+1=5(ч) – был в движении пароход
2) 24∙5=120(км) – расстояние, пройденное пароходом (катер прошёл столько же)
3) 120: 15=8(ч) – был в пути катер
4) 8-5 =3(ч) – время, которое пароход простоял на мели
Ответ: 3 часа пароход стоял на мели.
5 баллов
7. Три команды набрали на олимпиаде 285 баллов. Если бы команда школы №24 набрала на 8 баллов меньше, а команда школы №44 на 12 баллов меньше, команда школы №77 на 7 баллов меньше, то все они набрали бы поровну баллов. Сколько баллов набрали команды школ №24 и №77 вместе?
1) 8+7+12=27 (б)
2) 285-27=258(б)
3) 258:3=86(б)
4) 86+7=93(б)
5) 86+8=94(б)
6) 93+94=187(б)
Ответ: 187 баллов набрали команды школы №77 и №24 вместе.
5 баллов
8. Если сторону квадрата, периметр которого 36 см, уменьшить в 3 раза, то получится ширина прямоугольника, периметр которого 22 см. Найдите длину этого прямоугольника и вычислите площадь.
1) 36:4=9(см) – сторона квадрата
2) 9:3=3 (см) – ширина прямоугольника
3) 3*2=6 (см) – 2 ширины
4) (22-6):2= 8 (см) – длина прямоугольника
5) 8*3=24 (см)
Ответ: 24 квадратных сантиметров площадь прямоугольника.
5 баллов
9. Рысь съедает 600 кг мяса за 6 часов, а тигр в 2 раза быстрее. За какое время они съедят это мясо вместе?
1) 600:6=100(кг) – за 1 час съедает рысь
2) 100*2=200(кг) – за 1 час съедает тигр
3) 100+200=300(кг) – вместе за 1 час
4) 600:300=2 (ч)
Ответ: за 2 часа рысь и тигр съедят это мясо.
4 балла
10. 5 землекопов за 5 часов выкапывают 5 метров канавы. Сколько землекопов смогут за 100 часов выкопать 100 метров канавы?
Если за пять часов пять землекопов выкапывают 5 м канавы, то за 100 ч за время, в 20 раз большее) те же пять землекопов выкопают канаву в 20 раз длиннее, то есть 100 м канавы.
Ответ: 5 землекопов.
4 балла
Олимпиадные задания по математике для 4 класса с ответами
Олимпиадные задания по математике
4 класс (с ответами)
У доктора Пилюлькина есть лекарство в нескольких сосудах, масса которых 3г, 6г, 9г, 12г, 15, 18, 21г. Других сосудов у доктора нет. Помоги Пилюлькину раздать всё лекарство четверым больным поровну.
Если каждое следующее число на 1 больше предыдущего, то такие числа называют последовательными. Сумма четырёх последовательных чисел равна 318. Найди эти числа.
У Знайки имеются медные монеты в 1, 2, 3 и 5 копеек, которые весят соответственно 1г, 2г, 3г, 5г. Малышу известно, что среди четырёх медных (по одной каждого достоинства) имеется бракованная, меньшего веса. Как при помощи двух взвешиваний на чашечных весах без гирь Знайке определить бракованную монету?
Незнайка решил смастерить будку для своей собаки. У него есть два вида листов фанеры: размером 12х6 дм и размером 9х8 дм. Каждый лист нужно разрезать на 6 прямоугольников размером 4х3 дм. Какого вида листы выгоднее использовать Незнайке, чтобы общая протяжённость линий разреза была как можно меньше?
Пончик и Гусля весят столько, сколько 5 учебников. Гусля весит столько, сколько 4 кошки. Две кошки и Гусля весят столько, сколько 3 учебника. Сколько кошек уравновесят Пончика?
Торопыжка начертил три прямые линии. На каждой из них отметил три точки. Всего Торопыжка отметил 6 точек. Покажи, как он это сделал.
Ответы
1. Решение:
21 г — первому больному
18 + 3 = 21 г — второму больному
15 + 6 = 21 г — третьему больному
12 + 9 = 21 г — четвертому больному
Критерии оценивания:
правильный ответ с объяснением – 3 балла;
правильный ответ без объяснения – 1 балл;
задание не начато или выполнено неправильно – 0 баллов.
2. Решение:
Первый способ.
а + 1 — второе число
а + 2 — третье число
а + 3 — четвертое число
а + а + 1 + а + 2 + а + 3 = 318
4 а + 6 = 318
4 а = 318 – 6
4 а = 312
а = 312 : 4
а = 78 (первое число)
78 + 1 = 79 (второе число)
78 + 2 = 80 (третье число)
78 + 3 = 81 (четвертое число)
Второй способ.
318 : 4 = 79 (ост. 2) Значит 318 = 79 + 79 + 80 + 80 = (79 – 1) + 79 + 80 + (80 + 1) =
78 + 79 + 80 + 81
Критерии оценивания:
правильный ответ с решением – 5 баллов;
правильный ответ без объяснения – 2 балла;
задание не начато или выполнено неправильно – 0 баллов.
3. Решение:
На одну чашу весов поместим монеты 1 к. и 2 к., а на другую – 3 к. При равновесии чашек бракованная монета — 5 к. При нарушении равновесия монета находится в той чаше, которая выше. Пусть в верхней чаше монета 3 к. Тогда она – бракованная. Пусть в верхней чаше монеты 1к. или 2 к. Сделаем второе взвешивание: на одну чашу весов положим монеты 2 к. и 3 к., а на другую 5 к. Если весы в равновесии, то бракованная монета — 1 к. Если же вверх пойдёт чаша, на которой 2 к. и 3 к., то бракованная монета — 1к.
Возможен ещё один способ: сначала на одну чашу поместить монеты 2 к. и 3 к., а на другую – монету 5 к.
Критерии оценивания:
правильный ответ с объяснением – 4 балла;
правильный ответ без объяснения – 2 балла;
задание не начато или выполнено неправильно – 0 баллов.
4. Решение:
Для листов с размерами 12х6 длина всех разрезов равна 12 + 6 х 2 = 24 (дм).
Для листов с размерами 9х8 дм длина всех разрезов равна 9 + 8 х 2 = 25 (дм).
Критерии оценивания:
правильный ответ с объяснением – 4 балла;
правильный ответ без объяснения – 1 балл;
задание не начато или выполнено неправильно – 0 баллов.
5. Решение:
Обозначим Пончика – П, Гуслю – Г, учебник – У, кошку – К. Тогда согласно условия получим:
П + Г = 5У,
Г = 4К,
2К + Г = 3 У.
Тогда 2К + 4К = 3У или 2К = У.
П + 4К = 5У.
Так как У = 2К, то П + 4К = 10К и П = 6К.
Ответ: 6 кошек уравновесят Пончика.
Критерии оценивания:
правильный ответ с объяснением – 5 баллов;
правильный ответ без объяснения – 2 балла;
задание не начато или выполнено неправильно – 0 баллов.
6. Решение:
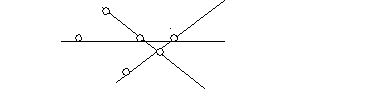
Критерии оценивания:
правильный ответ – 3 балла;
задание не начато или выполнено неправильно – 0 баллов.
Олимпиадные задачи по математике 4 класс. Часть 1. — Колпаков Александр Николаевич
Предлагаю свой тест для подготовки в математические школы: Курчатовская школа, Лицей Вторая школа, 179 школа и другие популярные лицеи / колледжи. Тест содержит только олимпиадные задачи и послужит репетитору по математике хорошим вспомогательным материалом для соответствующей работы. Последняя задача оценивается в 2 балла и имеет общее решение независимо от количество проведенных вниз линий. Если Вы репетитор — задайте ученику этот текст на дом и попросите его прислать результаты Вам на e-mail. Вам в почтовый ящик опустится полная копия странички с заданиями и проверкой правильности введенных ответов. Пользуйтесь также другими сервисами на моем сайте.
Задача 2. Можно ли получить число 234567898765432 умножением некоторого числа само на себя?
Выберите ответ:
Задача 3. Маруся выбирает несколько чисел из списка 1,2,3,4,5,6,7,8,9,10 так, чтобы ни какое выбранное число не было в 2 раза больше другого выбранного. Какую наибольшую сумму выбранных чисел она может при этом получить?
Ответ:
Задача 7. Учитель написал на листке бумаги число 40, а 27 учеников передают листок друг другу и каждый либо прибавляет к его числу 3, либо отнимает от него число 3. Может ли при этом получится число 42?
Выберите ответ:
Задача 10. Сколько треугольников на рисунке?
Ответ:
Я хочу отправить результаты на почту
Меня зовут
и я хочу отправить свои результаты
на e-mail
Если Вам нужен качественный курс подготовки к олимпиадам по математике — приезжайте в Строгино ко мне на индивидуальные уроки. Я заражу Вашего ребенка математикой с олимпиад, привью навыки решения нестандартных задач и тем самым помогу снять страх перед первым в жизни вступительным экзаменом (в любые школы). Будет построен индивидуальный учебный план с максимально широким охватом типов задач и подходов к ним. Я ориентируюсь на подготовку в Курчатовскую школу (она совсем недалеко от Строгино, в котором я живу), Лицей Вторая Школа, 179 школа. Этот список по ежегодной специализации, но его легко продолжить, ведь никакой особой специфики и стандарта по олимпиадным задачам каждой конкретной школой не выделяется. Просто напросто занимайтесь усложненной нестандартной математикой добросовестно и систематически. Тогда Вам будут открыты любые двери.
Олимпиадные задания по математике (4 класс) по теме: Школьный тур олимпиады по математике 4 класс с ответами
Школьный тур олимпиады по математике среди учащихся 4-х классов
Выполнил_ учени__ 4класса __ ____________________________________
1.Разминка. а) 1,2,3,4,5,6,7,8,9,0. Что больше сумма этих чисел или произведение? ___________________________________________________________________________б) Используя только цифры 0, 1, 3, 5 написать наибольшее и наименьшее четырёхзначные числа: ___________________________________________________________________ в) Трое играли в шашки. Сколько партий сыграл каждый, если всего сыграно 3 партии? __________________________________________________________________
2. Занимательные задачи. а) 60 листов книги имеют толщину 1 см. Какова толщина всех листов книги, если в ней 240 страниц? __________________________________________________________________________б) В соревнованиях по гимнастике Заяц, Мартышка, Удав и Попугай заняли первые 4 места. Определите, кто занял какое место, если известно, что Заяц стал вторым, Попугай не стал победителем, но в призёры попал, а Удав уступил Мартышке._________________________________________________________________________________________________________________________________________ в) Мальчик каждую букву своей фамилии заменил порядковым номером этой буквы в русском алфавите. Получилось число 3161312163. Какая фамилия у мальчика? _________________________________________________________________________ г) На расстоянии 5 м друг от друга в один ряд посажено 10 молодых деревьев. Найдите расстояние между крайними деревьями. ___________________________ __________________________________________________________________________
3. Думай, решай! а) Установи (не вычисляя) порядок действий в выражении:
70 000 – (64 000 : 128 — 3 280 : 164 ×15) ×70 + 192 000 : 800 = б) Выполни действия: 72 361 440 : 36 = _________________ 3 068 × 795 = ____________ 8 м 40 см : 1м 40 см = _______________ 20 ч 20 мин – 18 ч 32 мин = _____________ в) Рысь съедает 600 кг мяса за 6 часов, а тигр – в 2 раза быстрее. За какое время они съедят это мясо вместе? Объясни решение._________________________________ _________________________________________________________________________ _________________________________________________________________________ _______________________________________________________________________ _ г) Сиденье имеет вид квадрата со стороной 36 см. Составив в ряд 4 табурета, получили «журнальный столик». Какова его площадь и периметр? (Решение записать) ________________________________________________________________ _________________________________________________________________________ _________________________________________________________________________
4. Головоломки. а) «Магический квадрат».
________________________________________________________
б) «Головоломка с палочками». Составь из палочек такую же фигуру. Убери в ней четыре штуки, чтобы осталось три равных квадрата. Нарисуй решение.
Школьный тур олимпиады по математике среди учащихся 4-х классов. ОТВЕТЫ.
1.Разминка. а) 1,2,3,4,5,6,7,8,9,0. Что больше сумма этих чисел или произведение? (Сумма больше произведения, т.к. при умножении на 0 получается ноль) б) Используя только цифры 0, 1, 3, 5 написать наибольшее и наименьшее четырёхзначные числа: (5310, 1035) в) Трое играли в шашки. Сколько партий сыграл каждый, если всего сыграно 3 партии? (Две партии: 1и 2, 2и3,1и3)
2. Занимательные задачи. а) 60 листов книги имеют толщину 1 см. Какова толщина всех листов книги, если в ней 240 страниц? (240 страниц – это 120 листов. Листов в 2 раза больше, значит, и толщина книги будет тоже в 2 раза больше, т.е. 2 см) б) В соревнованиях по гимнастике Заяц, Мартышка, Удав и Попугай заняли первые 4 места. Определите, кто занял какое место, если известно, что Заяц стал вторым, Попугай не стал победителем, но в призёры попал, а Удав уступил Мартышке. (1 – Мартышка, 2 – Заяц, 3 – Попугай, 4- Удав) в) Мальчик каждую букву своей фамилии заменил порядковым номером этой буквы в русском алфавите. Получилось число 3161312163. Какая фамилия у мальчика? (Волков) г) На расстоянии 5 м друг от друга в один ряд посажено 10 молодых деревьев. Найдите расстояние между крайними деревьями. ( Т.к. деревьев 10., то промежутков между ними будет 9. Один промежуток составляет 5 м, значит,между крайними деревьями – 45 м.)
3. Думай, решай! а) Установи (не вычисляя) порядок действий в выражении:
70 000 – (64 000 : 128 — 3 280 : 164 ×15) ×70 + 192 000 : 800 = б) Выполни действия: 72 361 440 : 36 = 2 010 040 3 068 × 795 = 2 439 060 8 м 40 см : 1м 40 см =6 см 20 ч 20 мин – 18 ч 32 мин = 1 ч 48 мин в) Рысь съедает 600 кг мяса за 6 часов, а тигр – в 2 раза быстрее. За какое время они съедят это мясо вместе? Объясни решение 1) 600 : 6 = 100 (кг) – за час съедает рысь 2) 6:2 = 3 (ч)- ел тигр 3) 600:3= 200 (кг) – за час съедает тигр 4) 100+ 200=300 (кг) – съедают вместе рысь и тигр за час 5) 600:300=2(ч)
г) Сиденье имеет вид квадрата со стороной 36 см. Составив в ряд 4 табурета, получили «журнальный столик». Какова его площадь и периметр? (Решение записать) 1) 36×36= 1296 (кв. см) – площадь квадрата 2) 1296 ×35184 (кв.см) – площадь стола 3) (36×4 + 36) × 2= 360 (см)
4. Головоломки. (Сумма равна 54) (а) «Магический квадрат».
Б) «Головоломка с палочками». Составь из палочек такую же фигуру. Убери в ней четыре штуки, чтобы осталось три равных квадрата. Нарисуй решение.
|
|
Занятие по подготовке к олимпиаде по математике (4 класс)
Занятие по подготовке
к олимпиаде
Предмет: математика
Класс:4
Провела учитель
начальных классов
МБОУ СШ № 8 г. Выкса Колузанова Фаина Алексеевна
3.11. 2015 уч. год.
Цель: рассмотрение различных видов олимпиадных задач для улучшения самоподготовки к олимпиадам по математике.
Задачи:
Познакомить учащихся с понятиями логика и её составляющие: комбинаторика, классификация, сравнение, анализ, синтез.
Развитие мышления, логической речи, воображения, умения делать выводы.
Воспитание интереса к предмету, активности внимания.
Оптимальное развитие математических способностей у учащихся и привитие учащимся определенных навыков научно-исследовательского характера.
Расширение и углубление представлений учащихся о практическом значении математики.
Воспитание учащихся чувства коллективизма и умения сочетать индивидуальную работу с коллективной.
Оборудование: компьютер, мультимедийный проектор, экран, презентация к уроку.
Структура урока.
1.Создание атмосферы психологической комфортности.
2. Разминка.
3. Создание проблемной ситуации.
4. Решение задач на комбинаторику.
5. Физ. минутка.
6. Решение задач на классификацию.
7. Решение задач на анализ и синтез
8. Физ. минутка.
9. Решение заданий при помощи аналогии.
10. Решение логических задач.
12.Итог урока.
13. Оценка.
Ход мероприятия.
1.Создание атмосферы психологической комфортности.
Учитель:
Мы рады приветствовать вас в классе нашем
Возможно, есть классы и лучше и краше.
Но пусть в нашем классе вам будет светло,
Пусть будет уютно и очень легко!
— Мы рады приветствовать вас на нашем занятии по математике «Умники и умницы»
— Садитесь ребята!
— Проведем разминку для ума.
2. Разминка (Слайд №2)
1.Пять лампочек тускло горели в люстре. Хлопнули двери и две лампочки погасли. Сколько ламп осталось?
Ответ ученика. Пять. (Объяснить).
2. На столе стояли 3 стакана с ягодами. Вова съел один стакан ягод и поставил его на стол. Сколько стаканов осталось?
Ответ ученика. 3 стакана. (Объяснить).
3. В семье 7 братьев, у каждого по одной сестре. Сколько детей в семье?
Ответ ученика 8. (Объяснить).
4. Один ослик вёз 10 кг сахара. А другой ослик — 10 кг поп — корна. У кого поклажа была тяжелее? (Слайд №3)
Ответ ученика одинаково.
5. У бабушки Даши внучка Маша, кот Пушок, да пёс Дружок. Сколько у бабушки внучек?
Ответ ученика. Одна Маша.
6. Пассажир такси ехал за город. Навстречу ему прошли 5грузовиков, 3 легковые машины. Сколько всего машин шло за город?
Ответ ученика. Одна. Остальные ехали в город.
7. Наступил долгожданный январь. Сначала зацвела 1 яблоня, а потом ещё 3 сливы. Сколько деревьев зацвело? (Слайд №4)
Ответ ученика. В январе деревья не цветут.
3. Создание проблемной ситуации.
Учитель: — Каким должен быть ученик, чтобы решать эти задачи? (внимательным, сообразительным, с хорошей памятью, умение представлять эту задачу в реальной ситуации).
Учитель: — Мы на нашем занятии будем развивать эти качества ума.
Учитель: — «Математику уже затем учить следует, что она ум в порядок приводит»- говорил Михаил Васильевич Ломоносов. ( Слайд №5)
Портрет М. В. Ломоносова (Слайд №6)
— Желаю всем привести «ум в порядок» и показать свои хорошие знания.
— Начнём с решения задач на комбинаторику.
4. Решение задач на комбинаторику. Слайд№7
— Кто знает или может быть догадался, что означает слово комбинаторика?
Комбинаторика – это перебор возможных вариантов. (Слайд № 8)
Работа в парах
Учитель: — У вас на партах лежат листочки с заданиями.
— Прочитайте первое задание. (Слайд № 9)
— Попробуйте, выполните его в парах.
1. Составьте способом перебора возможных вариантов все возможные
а) двузначные числа из цифр 3, 4, 5. Цифры не должны повторяться.
Ученик записывает ответ на доске.
Ответ: а) 34, 35, 43, 45, 53, 54; (Слайд№10)
— Покажите у кого такие же ответы.
2. Запишите все трёхзначные числа, у которых сумма цифр равна 4? (Слайд№11)
— Назовите, какие числа вы записали?
Ответ: (112,121,211,202,220,301,310,103,400) (Слайд№12)
Работа в группах (Слайд№13)
— А сейчас поиграем в игру, которая называется « В кинотеатре». Для этого разделимся на группы по 5 человек. Один из вас будет играть роль кассира, а четыре участника – роль зрителей.
Билет в кинотеатр стоит 50р. у двух участников по 50р, а у других по 100р. На начало работы денег в кассе нет. В какой последовательности зрители должны купить билеты, чтобы двое из них получили сдачу?
— Кто забыл, задание прочитайте на листочках.
Ответ: А) 50, 100, 50, 100 Б) 50, 50, 100, 100 (Слайд№14)
5. Физминутка. (Слайд №15)
— Переходим к заданиям на классификацию.
6. Решение задач на классификацию. (Слайд №16)
— Что значит классификация?
Классификация – это распределение предметов по группам путем выделения в данных предметах тех или иных признаков. (Слайд №17)
Работа в парах
— Выполните следующее задание в парах.
1. Найдите общие свойства в последовательности чисел. Продолжи ряд, записав три последующих числа. (Слайд №18)
а) 2, 7, 4, 9, 6, 11, …(13, 10, 15) — (+ 5 , -3)
б) 45, 36, 28, 21, … (15, 10, 6) — (-9, -8, -7)
в) 1, 4, 9, 16, 25, … (36, 49, 64) — (1х1=1, 2х2=4, 3х3=9)
г) 20,12, 19, 14, 18, 16, … (17, 18, 15) — (через одного -1, +2)
Учитель: Кто догадался, какая связь между числами?
— Ответ к каждому ряду записывают на доске.
— Покажите сигналами, кто согласен.
Слайд №19.
2. Проверьте правильность следующих классификаций. (Слайд №20)
Даны три понятия, между первыми двумя существует определенная связь, между третьим и одним из предложенных существует аналогичная связь, надо найти четвертое слово:
а) вправо – влево, вверх — … (вниз)
б) сложение – сумма, деление — …(частное – результат деления)
в) уменьшаемое – вычитаемое, делимое — …(делитель – 2 компонент арифметического действия деления)
(Слайд №21)
— Переходим к следующему виду заданий.
7. Решение задач на анализ и синтез. (Слайд№22)
Анализ – это расчленение целого на части. (Слайд№23)
Синтез – мысленное объединение частей в целое. В мыслительной деятельности анализ и синтез дополняют друг друга. (Слайд№24)
1. — Сколько всего квадратов? (14) (Слайд№25)
Коллективная работа
2. У Милы вчетверо больше кукол, чем у Лены, а у Лены на 12 кукол меньше, чем у Милы. Сколько кукол у Милы? (Сделать чертеж к задаче.)
(Слайд№26)
— Про кого говорится в задаче? (Про Милу и Лену).
— Как обозначим имена девочек?
— При помощи чего обозначим количество кукол на чертеже у Милы и Лены?
-Что сказано про куклы у Милы? (Их вчетверо больше, чем у Лены).
— Значит, на сколько частей разделим отрезок?
— Что сказано про куклы у Лены?
— Почему у Лены на 12 меньше, чем у Милы? (У неё 1 часть, а у Милы 4 части).
— Что мы можем сказать про количество кукол у Милы? ( У неё столько же, сколько у Лены да ещё 12.)
Значит ,12 соответствуют, сколько частей? (3 части). Слайд №27
— Что отсюда мы можем узнать? (Сколько кукол в одной части).
12:3=4 (к.) – в одной части.
4х4=16 (к) – у Милы.
Учитель: Запишите ответ.
— Пришло время отдохнуть.
8. Физ. минутка. Слайд №28
— Выполним задания при помощи аналогии.
9. Решение заданий при помощи аналогии. Слайд №29
Аналогия – это мыслительная операция, с помощью которой находится сходство между объектами в некотором отношении. Слайд №30
Самостоятельная работа
1. Шестиклеточный логикон. Слайд №31
— Сравнивая информацию в верхних клетках и в нижних, найдите в ней логическую связь. По аналогии заполните пустую клетку.
36
81
45
4
9
?
Ответ: “5”, 36:9=4, 81:9=9, 45:9=5.
25
15
45
7
6
?
Проверка по слайду. Ответ: “9”,.2+5=7, 1+5=6, 4+5=9. Слайд №32
— Покажите у кого такие же ответы.
— Следующий этап нашей работы это решение логических задач.
10. Решение логических задач. Слайд №33
Работа в группах.
— Объединитесь в группы по 4 человека.
— На столах лежат таблицы. Заполните их.
Слайд №34
Белов
Чернов
Рыжов
белые волосы
чёрные волосы
рыжие волосы
Встретились три мальчика. Познакомились. Оказалось, что их фамилии Белов, Чернов, Рыжов.
— Вы только посмотрите, — воскликнул Белов. – У одного из нас белые, у одного чёрные и у одного рыжие волосы, но ни у кого цвет волос не совпадает с тем, на который указывает фамилия!
— Ты прав, — ответил ему черноволосый мальчик.
-Определите, какой цвет волос у каждого мальчика.
Проверка по слайду. Слайд №35
— Кто объяснит, как заполнял таблицу?
— Мы должны из текста выбрать нужную информацию. Какая информация есть в тексте? (В тексте Белов говорит, что цвет волос не совпадает с тем, на который указывает фамилия. Значит, у Белова не белые волосы, у Чернова не чёрные волосы, а у Рыжова не рыжие волосы. Ставим прочерки.)
— Кто с ним согласился? (черноволосый мальчик.)
-Белов мог ответить сам себе? (нет) Что из этого следует? (Значит, у него волосы не могут быть чёрного цвета?) Ставим прочерки, у Белого не могут быть волосы чёрного цвета.
— Значит волосы у Белова рыжего цвета, ставим +
— А у нас цвета волос могут повторяться? Значит, у Чернова могут волосы быть тоже рыжего цвета? (нет) Ставим прочерк Чернову, что у него не могут быть волосы рыжего цвета.
-Тогда какой цвет ему остаётся? (белый) Ставим +, который показывает, что у Чернова волосы белого цвета.
— Тогда какой цвет волос у Рыжова? Т.к. у Чернова волосы белого цвета, а цвета у нас не должны повторяться, отсюда следует, что у него волосы не могут быть белого цвета, ставим прочерк. Остался чёрный цвет волос, которые и принадлежат Рыжову. Ставим +. Слайд №36
Белов
Чернов
Рыжов
белые волосы
————
+
—————
чёрные волосы
————
————
+
рыжие волосы
+
————-
————
10. Умение самостоятельно предполагать, какая информация нужна для решения учебной задачи. Слайд №37
1. У котят и цыплят 42 ноги и 12 голов. Сколько было котят и сколько было цыплят?(9 котят и 3 цыплёнка.) Слайд №38
Слайд №39
2. С хозяйством попа справлялись 10 работников. Каждый работник в день съедает каравай хлеба и другие продукты. Поп принял на работу Балду.
Живет Балда в поповом доме,
Спит себе на соломе,
Ест за четверых,
Работает за семерых
Поп прогнал лишних работников.
Сколько хлеба экономил поп ежедневно?
(Работает за 7, значит должен получать 7 караваев. А съедает за четверых. 7-4=3. Получается экономил поп ежедневно 3 каравая).
12.Итог урока. Чем мы занимались на уроке? (развивали логику)
13. Оценка.
— Оцените свою работу.
— Прочитайте 1предложение.
Урок полезен все понятно.
Лишь кое-что чуть- чуть неясно.
Ещё придется потрудиться.
Да, трудно всё-аки учиться.
— Кто считает, что урок был полезен, ставит рядом с этим предложением+
Аналогично выполняют работу с остальными предложениями.