Мини справочник по математике для учащихся 5 класса
Мини справочник по математике для учащихся 5 класса может быть истольован как шпаргалка или как справочный матемиал. Справочник состоит из следующих блоков:
1. Свойства натуральных чисел.
2.Алгоритм решения уравнений.
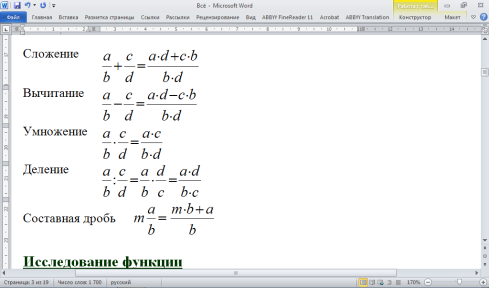
3.Обыкновенные дроби.
4. Формулы.
5.Элементы геометрии.
6. Единицы измерения
Просмотр содержимого документа
«Мини справочник по математике для учащихся 5 класса »
Мини-справочник
по математике
5 класс

Автор
Гартун
Тамара Константиновна
учитель математики
2013 г.







Свойства натуральных чисел
Решение уравнений
Обыкновенные дроби
Свойства сложения:
Переместительное а + Ь = Ь + а
Сочетательное а + (Ь + с) = (а + Ь) + с
а + 0 = 0 + а = а
Свойства вычитания:
Вычитание суммы из числа
а — (Ь + с) = а — Ь — с
Вычитание числа из суммы
(а + Ь) — с = а + (Ь — с) (а + Ь) — с = (а — с) + Ь
а — 0 = а
а — а = 0
Свойства умножения:
Переместительное а • Ь = Ь • а
Сочетательное а • (Ь • с) = (а • Ь) • с
Распределительное
(а + Ь) с = ас + Ьс (а — Ь) с = ас — Ьс
1 • п = п • 1 = п
0 • п = п • 0 = 0
Свойства деления:
а : 1 = а
а : а = 1
0 : а = 0
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое
х + а = Ь х = Ь — а
Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность
х — а = Ь х = а + Ь
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность
Ь — х = а х = Ь — а
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель
а • х = Ь х = Ь : а
Чтобы найти неизвестное делимое, надо делитель умножить на частное
х : а = Ь х = а • Ь
Чтобы найти неизвестный делитель, надо делимое разделить на частное
а : х = Ь х = а : Ь
а Ь а + Ь а Ь
с с с с с
а— Ъ
Формулы
Формула пути
5 = V • 1 V = 5 : 1 1 = 5 : V
Площадь
5 — путь (расстояние)
V — скорость
1 — время
Прямоугольник
5 = а • Ь

5 = а • а = а2
Объём

V = аЬс
V = а3
Ь
а
а
а
с
а
Шпаргалка по математике — Математика






1 см = 10 мм
1 дм = 10 см = 100 мм
1 м = 10 дм = 100 см
1 км = 1000 м

1 см = 100 мм
1 дм = 100 см = 10000 мм
1 м = 100 дм = 10000 см
1 км = 1000 000 м
1 км = 100 га = 10000 а
1 а = 100 м = 10000 дм
1 га = 100 а = 10000 м


Торт весит 720 граммов. Сколько весят три куска этого торта?
- Найди 1 долю (целое раздели на количество долей): 720 : 8 = 90 (г)
- 1 долю умножь на необходимое количество: 90 × 3 = 270 (г)

1 кг = 1000 г
1 ц = 100 кг
1 т = 10 ц = 1000 кг

1 мин = 60 с
1 ч = 60 мин
1 сут. = 24 ч
1 г. = 12 мес.
1 век = 100 лет
 17350 2. Если количество цифр одинаково, то начинай сравнение с самого большого разряда. 3 58 741 2 58 741 6 4 3 74 7 3 74 173 4 90 173 5 00 «
17350 2. Если количество цифр одинаково, то начинай сравнение с самого большого разряда. 3 58 741 2 58 741 6 4 3 74 7 3 74 173 4 90 173 5 00 «
1. Сравни количество цифр в числе. Больше то число, в котором больше цифр.
173490 17350
2. Если количество цифр одинаково, то начинай сравнение с самого большого разряда.
3 58 741 2 58 741
6 4 3 74 7 3 74
173 4 90 173 5 00

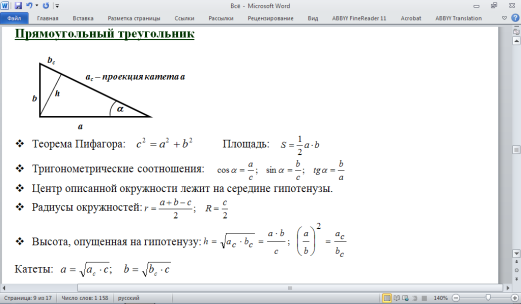
Диагонали прямоугольника равны (АС = В D )
Точка пересечения диагоналей делит каждую из них на 2 равные части (АО = ОС, ВО = О D )

— расстояние
— время
— скорость


1) V c б = V 1 + V 2
2) s = t × V сб

1) V c б = V 1 + V 2
2) t = s : V сб

1) V c б = S : t
2) V 1 = V сб – V 2


- Умножаем число на единицы, записывая результат так же, как при умножении на 1-зн. число.
- Умножаем число на десятки, начиная записывать результат под десятками.
- Складываем два неполных произведения, соблюдая порядок их записи

- Определи количество цифр в частном
- Раздели 1-ое неполное делимое
- Найди остаток и сравни его с делителем
- Если остаток меньше делителя, снеси следующую цифру и раздели получившееся число.

Класс миллиардов
Сот. млрд.
Дес. млрд.
XII
XI
Ед. млрд.
Класс миллионов
Сот.мил.
X
IX
Дес.мил.
Ед. мил.
VIII
Класс
тысяч
Сот. тыс.
VII
5
VI
3
0
Дес. тыс.
0
4
Класс единиц
Ед. тыс.
V
9
IV
7
Сот.
6
0
0
0
III
8
Дес.
5
3
4
II
Ед.
0
4
I
0
0
0
4
5
0
0
Шпаргалка по математике-50 тем
Определение: Последовательность, у которой задан первый член a1, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией:
an+1 = an + d, где d – разность прогрессии.



Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
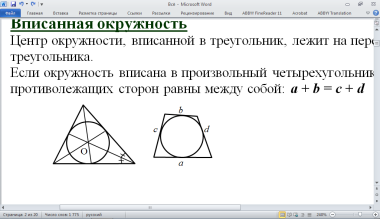
Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
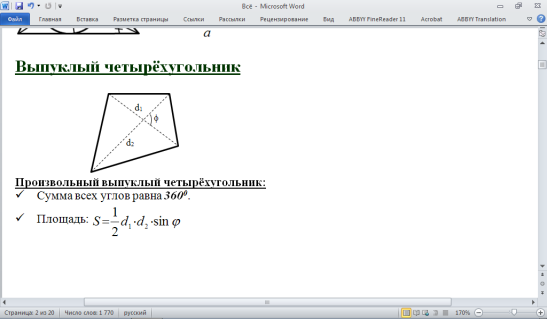
Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c + d
Определение: Последовательность, у которой задан первый член b1 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q 0, называется геометрической прогрессией:
bn+1 = bn q, где q – знаменатель прогрессии.

Формула деления с остатком: n = mk + r,
где n – делимое, m — делитель, k — частное, r – остаток: 0 r < m
Любое число можно представить в виде:
n = 2k + r, где r = {0; 1}
или n = 4k + r, где r = {0; 1; 2; 3}
Пусть n : m = k, где n, m, k – натуральные числа.
Тогда m – делитель числа n, а n – кратно числу m.
Число n называется простым, если его делителями являются
только единица и само число n.
Множество простых чисел: {2; 3; 5; 7; 11; 13; . . .; 41; 43; 47 и т.д.}
Числа n и m называются взаимно простыми, если у них нет общих делителей, кроме единицы.
Стандартный вид: 317,3 = 3,173 102 ; 0,00003173 = 3,173 10-5
Форма записи: 3173 = 3 1000 + 1 100 + 7 10 + 3
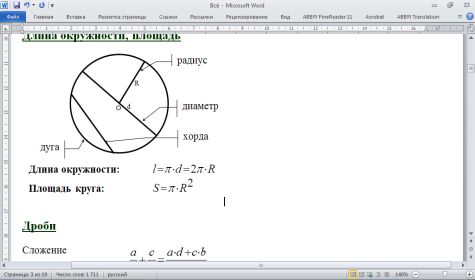
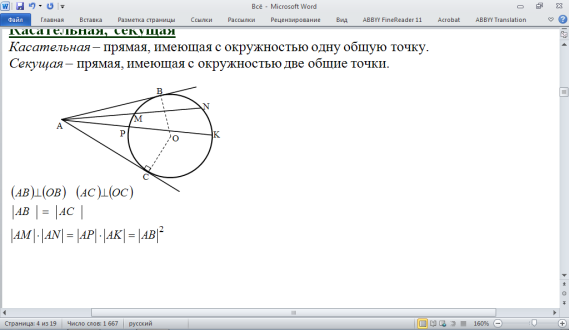
Касательная – прямая, имеющая с окружностью одну общую точку.
Секущая – прямая, имеющая с окружностью две общие точки.
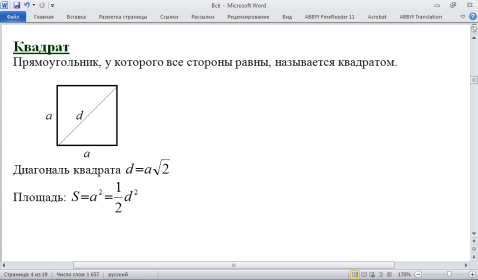
Прямоугольник, у которого все стороны равны, называется квадратом.

y = kx + b, k – угловой коэффициент, b – свободный член

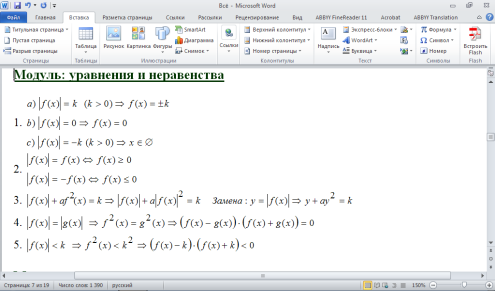

Определения:
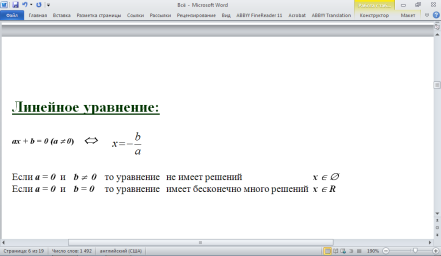
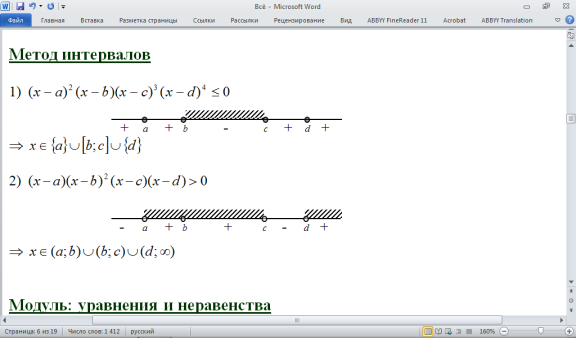
Неравенством называется выражение вида:
a < b (a b), a > b (a b)
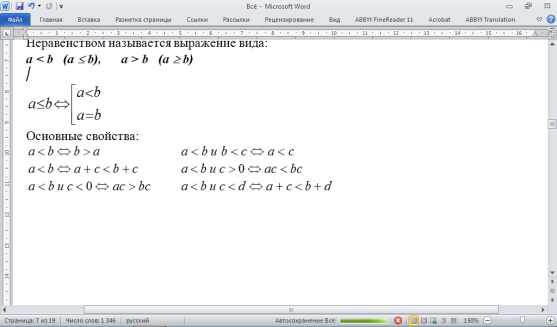
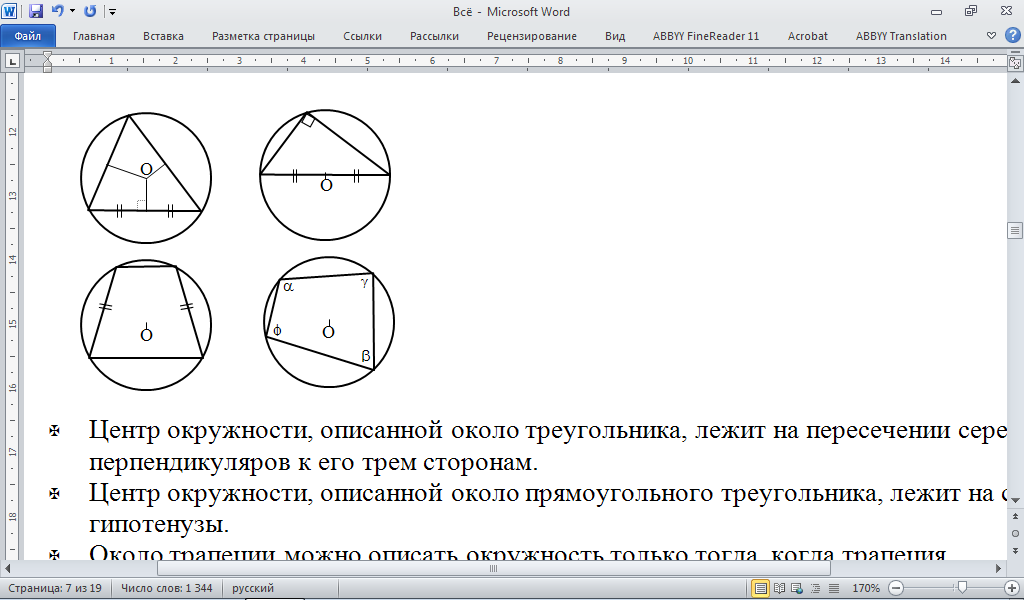
-Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.
-Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
-Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
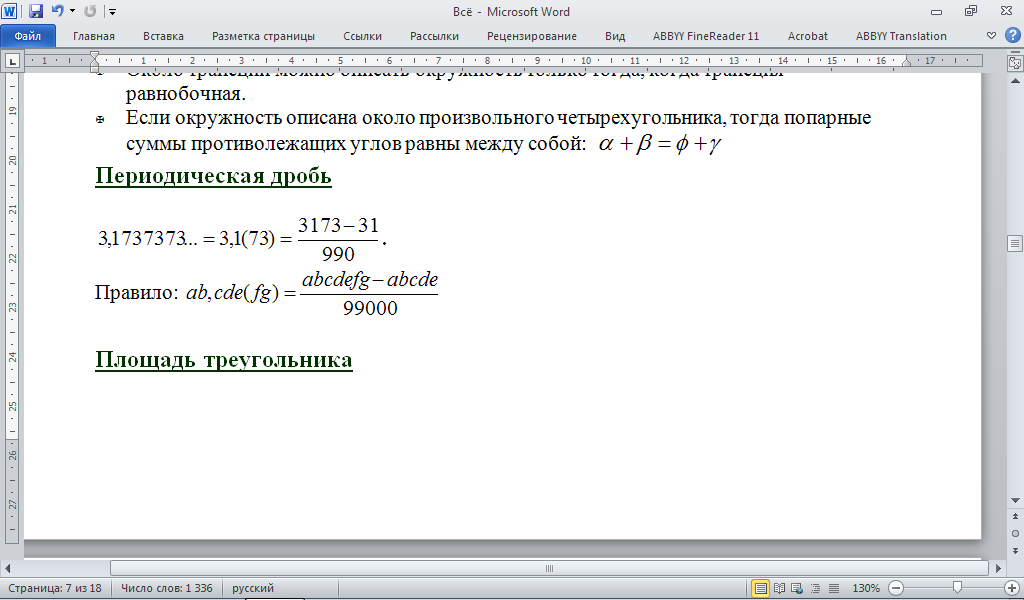
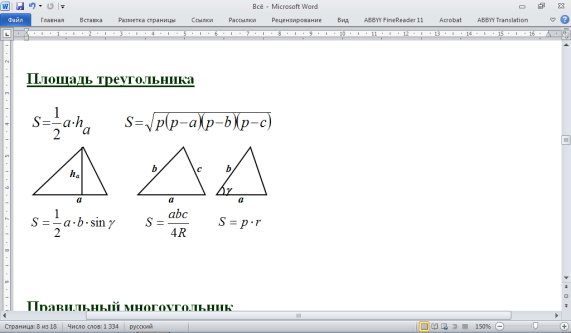
-Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой: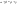
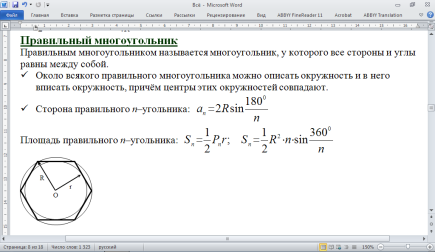
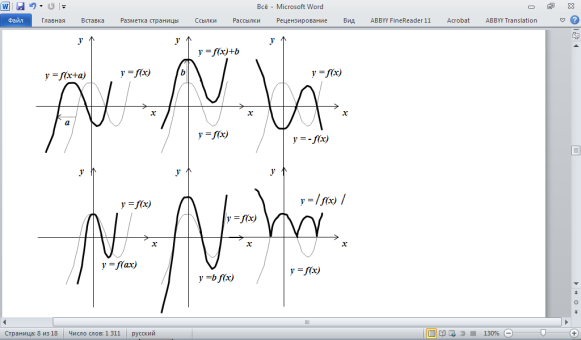
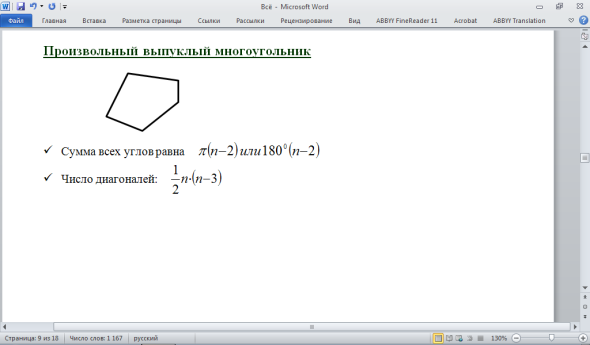
Правильным многоугольником называется многоугольник, у которого все стороны и углы равны между собой.
Около всякого правильного многоугольника можно описать окружность и в него вписать окружность, причём центры этих окружностей совпадают.

Процентом называется сотая часть от числа. 1%A = 0,01A
Основные типы задач на проценты:
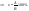 Сколько процентов составляет число A от числа B?
Сколько процентов составляет число A от числа B?
B — 100%
Сложные проценты.
Число A увеличилось на 20%, а затем полученное число уменьшили на 25%.
Как, в итоге, изменилось исходное число?
A1 = (100% + 20%)A = 120%A = 1,2A
A2 = (100% — 25%)A1=75%A1 = 0,75A1 = 0,751,2A = 0,9A = 90%A
A1 – A = 90%A – 100%A = -10%A
Ответ: уменьшилось на 10%.
Изменение величины.
Как изменится время, если скорость движения увеличится на 25%?
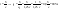
Ответ: уменьшится на 20%
треугольник, у которого две стороны равны.
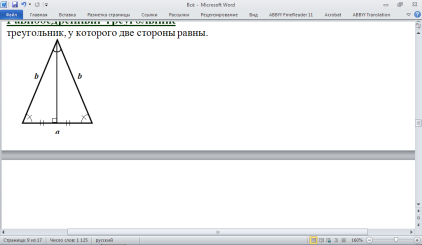
Углы, при основании треугольника, равны
Высота, проведенная из вершины, является биссектрисой и медианой.
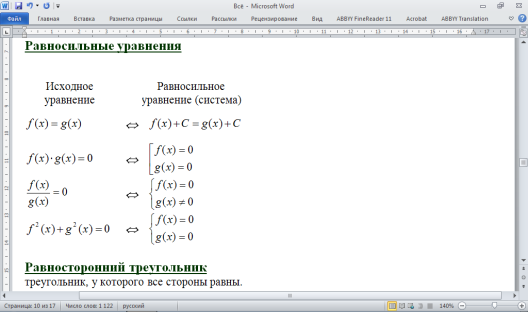
треугольник, у которого все стороны равны.
-Все углы равны 600.
-Каждая из высот является одновременно биссектрисой и медианой.
 -Центры описанной и вписанной окружностей совпадают.
-Центры описанной и вписанной окружностей совпадают.
-Радиусы окружностей:
-Площадь 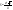
Параллелограмм, все стороны которого равны называется ромбом.
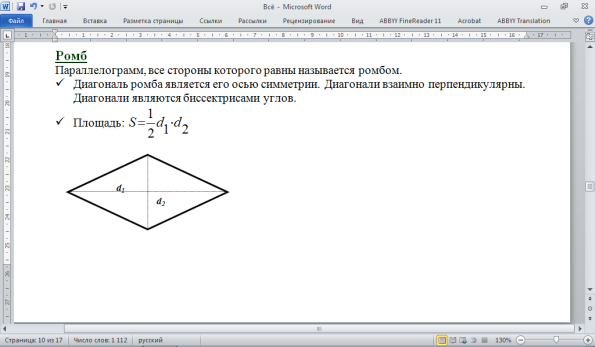
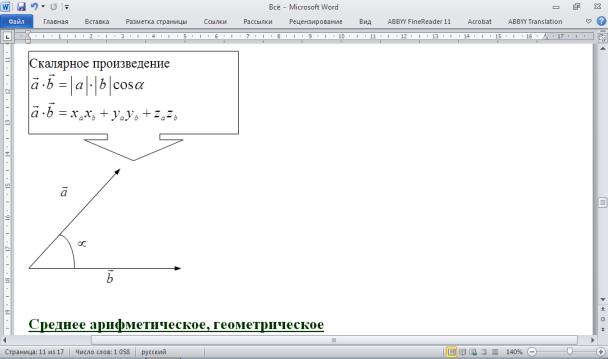
Среднее арифметическое:
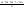
Среднее геометрическое: 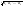
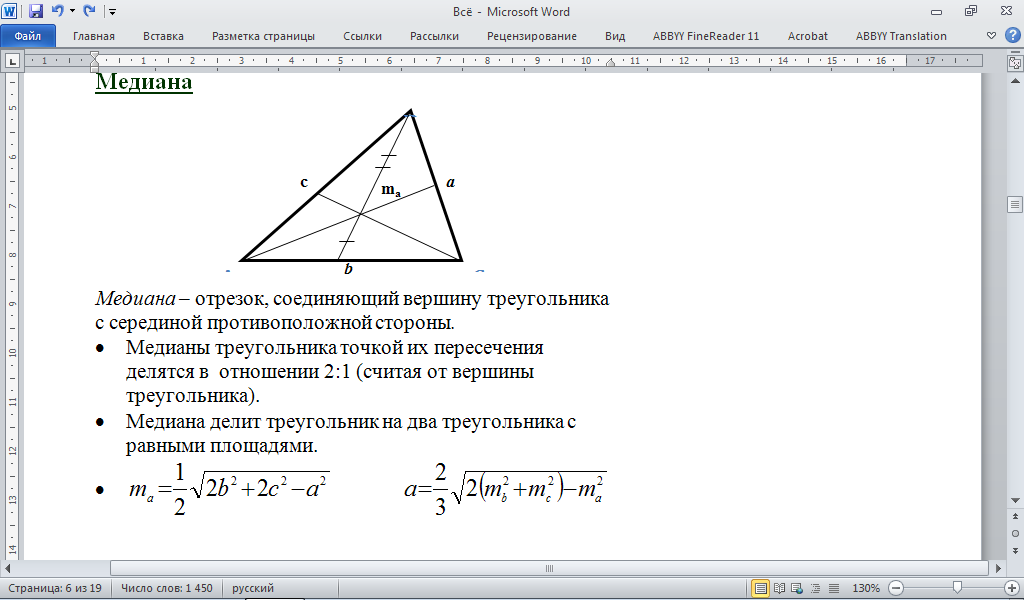
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
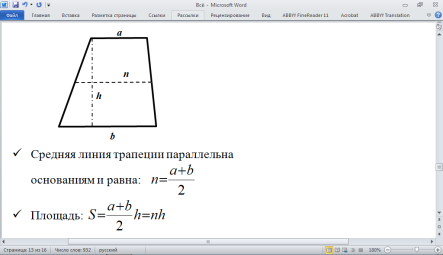
Средняя линия параллельна третьей стороне и равна её половине:

Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
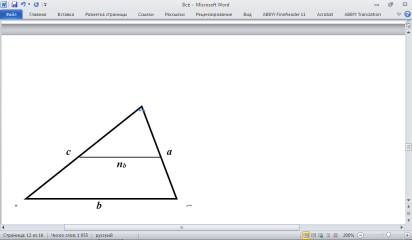

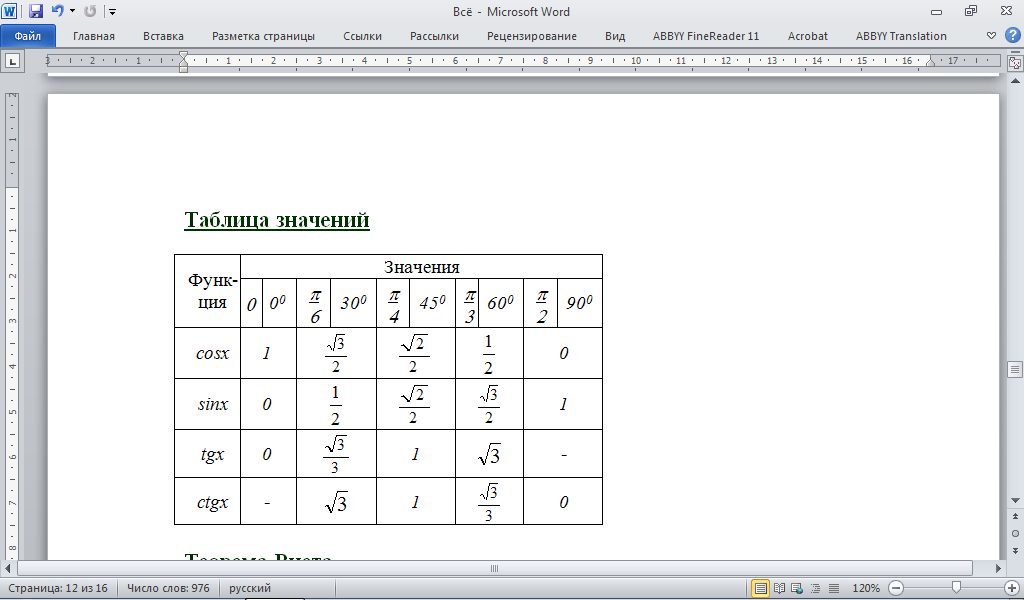
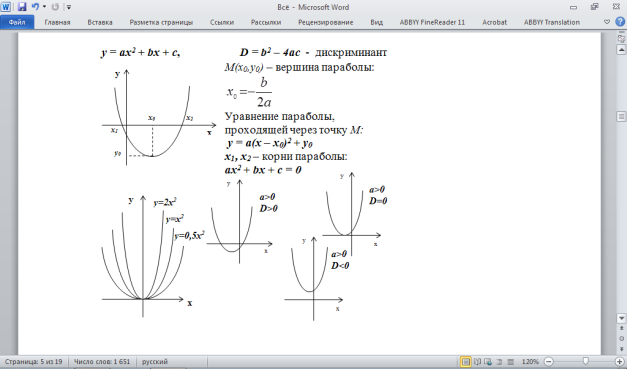
Приведенное квадратное уравнение: x2 + px + q = 0
x1 + x2 = — p
x1 x2 = q
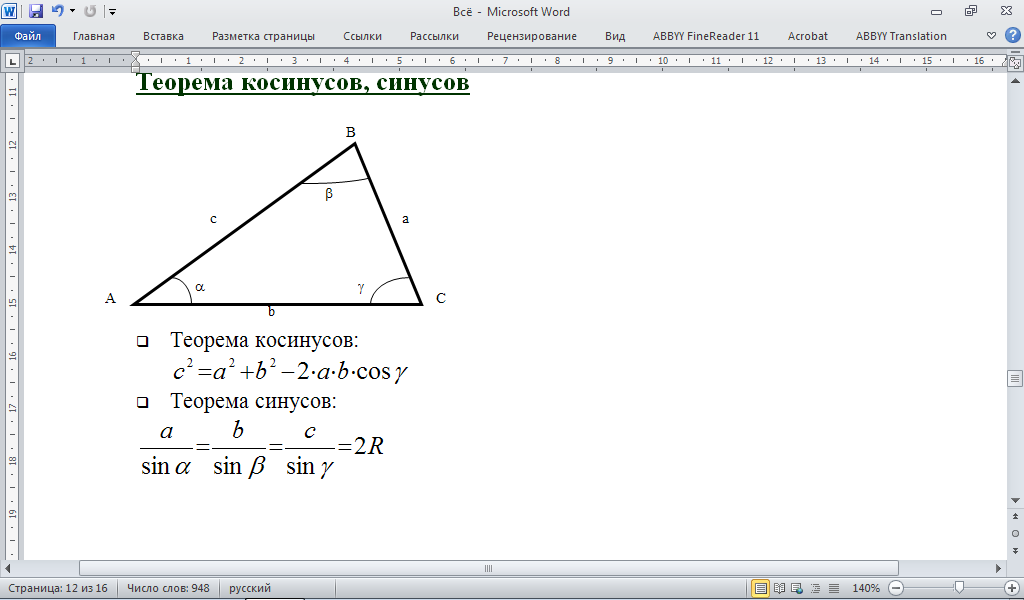
2.
Четырёхугольник, у которого две стороны
параллельны, а другие не параллельны,
называется трапецией.
Квадрат суммы
(a + b)2 = a2 + 2ab + b2
Квадрат разности
(a — b)2 = a2 — 2ab + b2
Разность квадратов
a2 – b2 = (a + b)(a – b)
Куб суммы
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Куб разности
(a — b)3 = a3 — 3a2b + 3ab2 — b3
Сумма кубов
a3 + b3 = (a + b)( a2 — ab + b2)
Разность кубов
a3 – b3 = (a – b)( a2 + ab + b2)
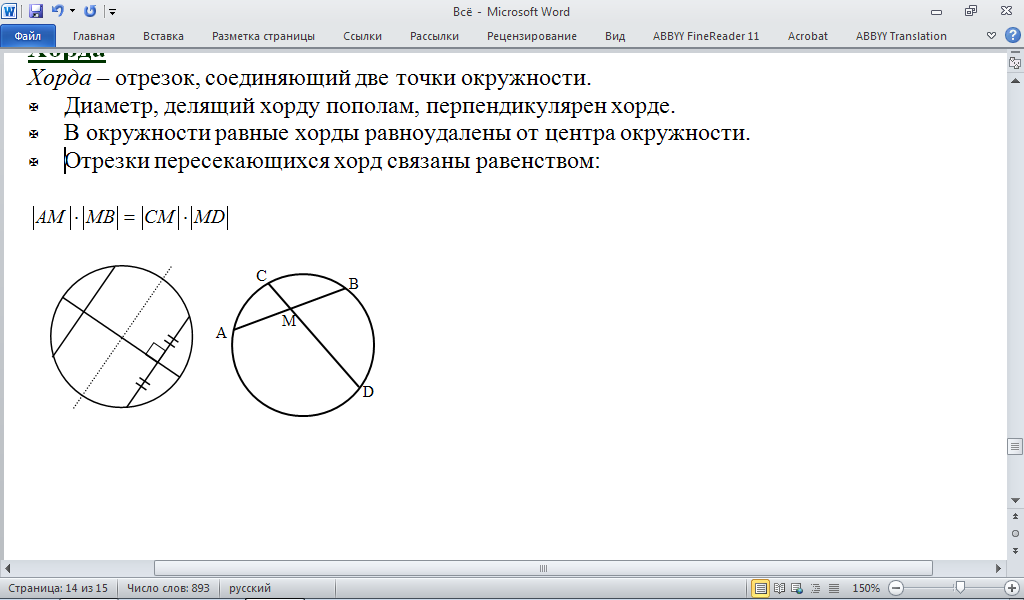
Хорда – отрезок, соединяющий две точки окружности.
-Диаметр, делящий хорду пополам, перпендикулярен хорде.
-В окружности равные хорды равноудалены от центра окружности.
-Отрезки пересекающихся хорд связаны равенством:
Шпаргалка по математике — Математика






1 см = 10 мм
1 дм = 10 см = 100 мм
1 м = 10 дм = 100 см
1 км = 1000 м

1 см = 100 мм
1 дм = 100 см = 10000 мм
1 м = 100 дм = 10000 см
1 км = 1000 000 м
1 км = 100 га = 10000 а
1 а = 100 м = 10000 дм
1 га = 100 а = 10000 м


Торт весит 720 граммов. Сколько весят три куска этого торта?
- Найди 1 долю (целое раздели на количество долей): 720 : 8 = 90 (г)
- 1 долю умножь на необходимое количество: 90 × 3 = 270 (г)

1 кг = 1000 г
1 ц = 100 кг
1 т = 10 ц = 1000 кг

1 мин = 60 с
1 ч = 60 мин
1 сут. = 24 ч
1 г. = 12 мес.
1 век = 100 лет
 17350 2. Если количество цифр одинаково, то начинай сравнение с самого большого разряда. 3 58 741 2 58 741 6 4 3 74 7 3 74 173 4 90 173 5 00 «
17350 2. Если количество цифр одинаково, то начинай сравнение с самого большого разряда. 3 58 741 2 58 741 6 4 3 74 7 3 74 173 4 90 173 5 00 «
1. Сравни количество цифр в числе. Больше то число, в котором больше цифр.
173490 17350
2. Если количество цифр одинаково, то начинай сравнение с самого большого разряда.
3 58 741 2 58 741
6 4 3 74 7 3 74
173 4 90 173 5 00

Диагонали прямоугольника равны (АС = В D )
Точка пересечения диагоналей делит каждую из них на 2 равные части (АО = ОС, ВО = О D )

— расстояние
— время
— скорость


1) V c б = V 1 + V 2
2) s = t × V сб

1) V c б = V 1 + V 2
2) t = s : V сб

1) V c б = S : t
2) V 1 = V сб – V 2


- Умножаем число на единицы, записывая результат так же, как при умножении на 1-зн. число.
- Умножаем число на десятки, начиная записывать результат под десятками.
- Складываем два неполных произведения, соблюдая порядок их записи

- Определи количество цифр в частном
- Раздели 1-ое неполное делимое
- Найди остаток и сравни его с делителем
- Если остаток меньше делителя, снеси следующую цифру и раздели получившееся число.

Класс миллиардов
Сот. млрд.
Дес. млрд.
XII
XI
Ед. млрд.
Класс миллионов
Сот.мил.
X
IX
Дес.мил.
Ед. мил.
VIII
Класс
тысяч
Сот. тыс.
VII
5
VI
3
0
Дес. тыс.
0
4
Класс единиц
Ед. тыс.
V
9
IV
7
Сот.
6
0
0
0
III
8
Дес.
5
3
4
II
Ед.
0
4
I
0
0
0
4
5
0
0