Контрольная работа для учеников 5 класса «Действия с обыкновенными дробями».
Контрольная работа
Все действия с обыкновенными дробями.
Вариант 5.
1. Вычислите:
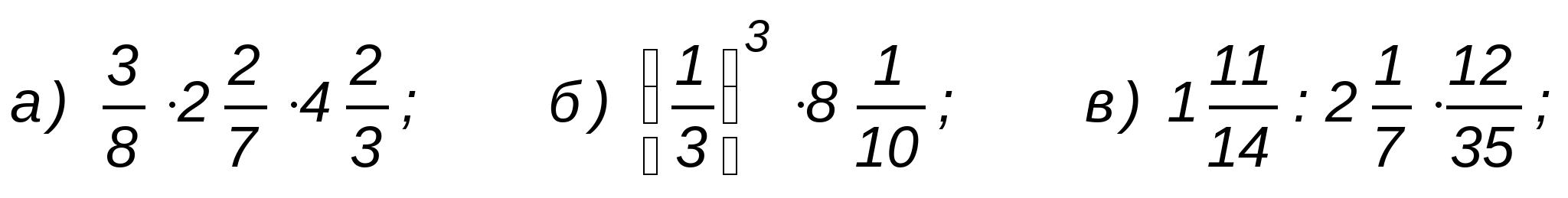
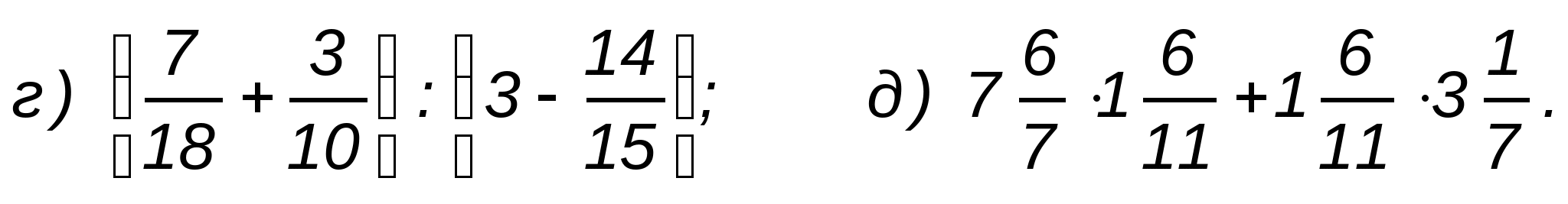
2. Решите уравнения:
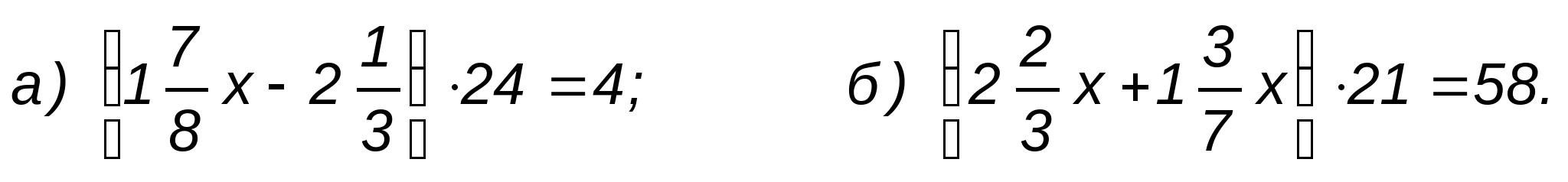
3. На овощной базе было 1080 тонн картофеля. В первый день отправили в магазины 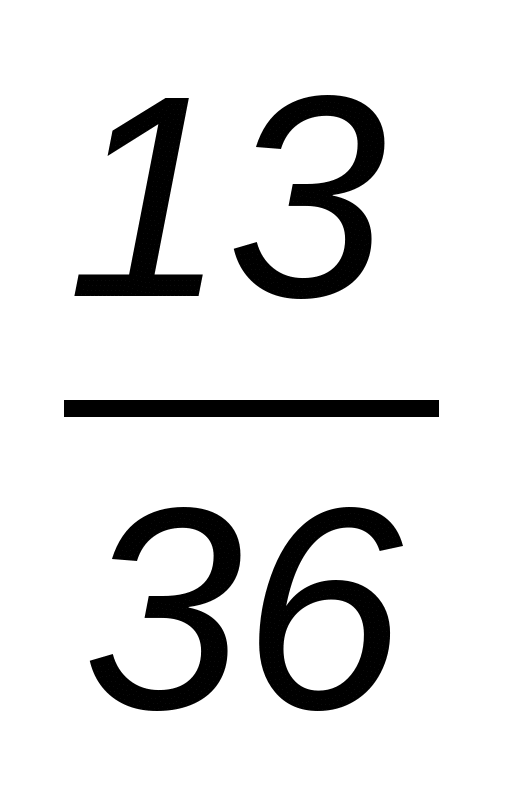 всего картофеля, а во второй —
всего картофеля, а во второй — 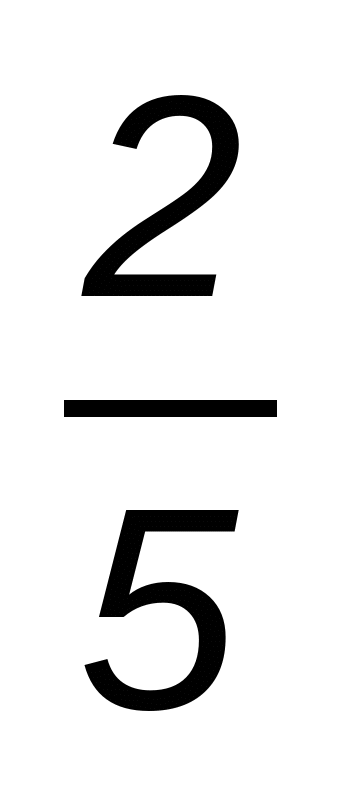 остатка. Сколько тонн картофеля отправили в магазины во второй день?
остатка. Сколько тонн картофеля отправили в магазины во второй день?
4. Три бригады пропалывали кукурузу. Первая бригада прополола 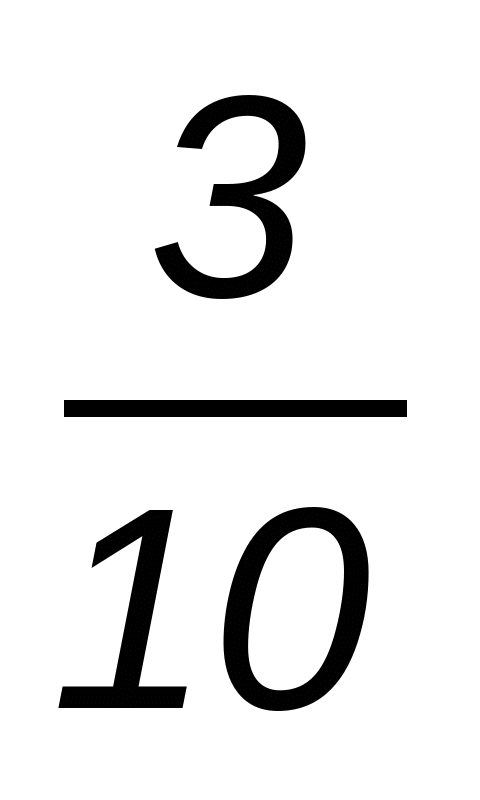 всей площади, вторая —
всей площади, вторая — 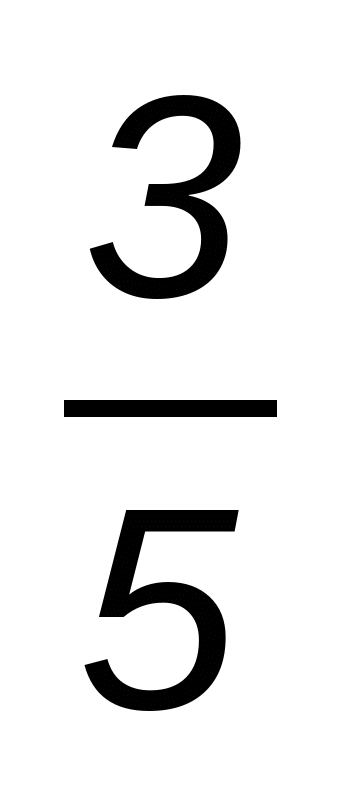 того, что прополола первая, а третья -остальные 624 га. Сколько всего гектаров занимает кукуруза?
того, что прополола первая, а третья -остальные 624 га. Сколько всего гектаров занимает кукуруза?
5. Рабочий выполняет дневную норму за 8 часов, а его ученик работает в 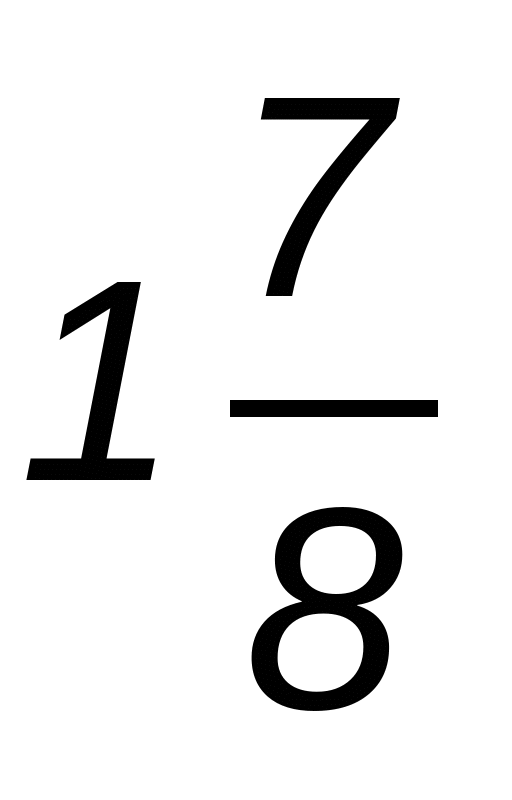 раза медленнее. Успеют ли они выполнить норму за 5 часов, если будут работать вместе?
раза медленнее. Успеют ли они выполнить норму за 5 часов, если будут работать вместе?
Дополнительное задание (оценивается отдельно):
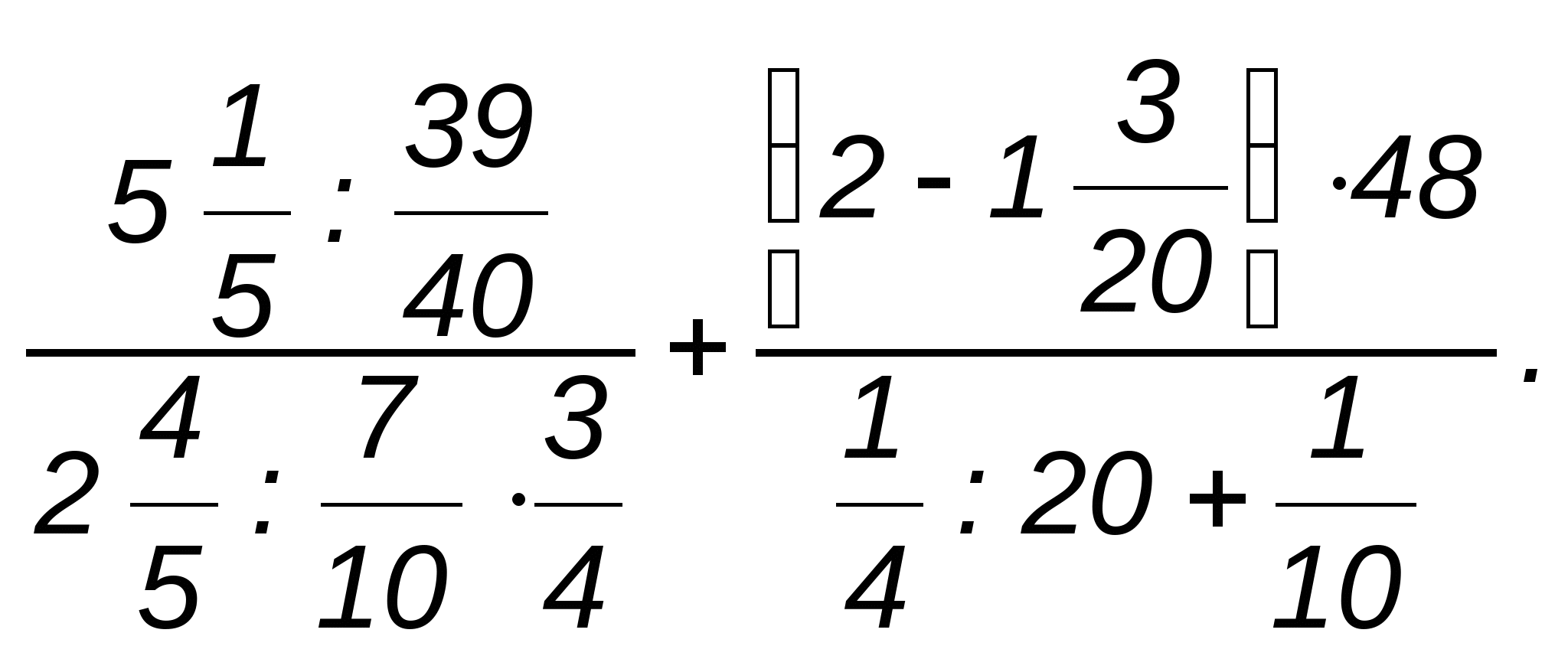
Контрольная работа
Все действия с обыкновенными дробями.
Вариант 6.
1. Вычислите:
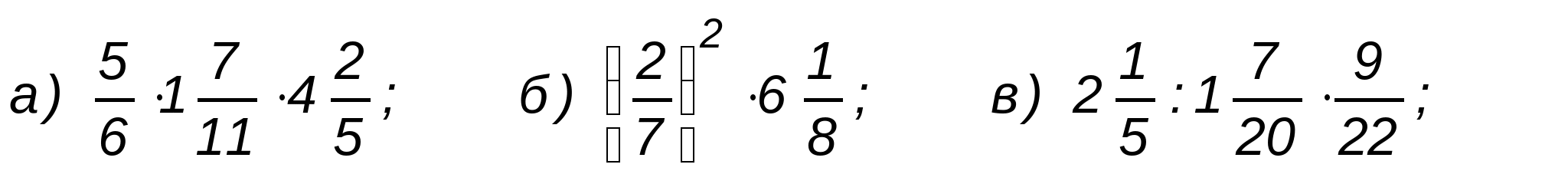
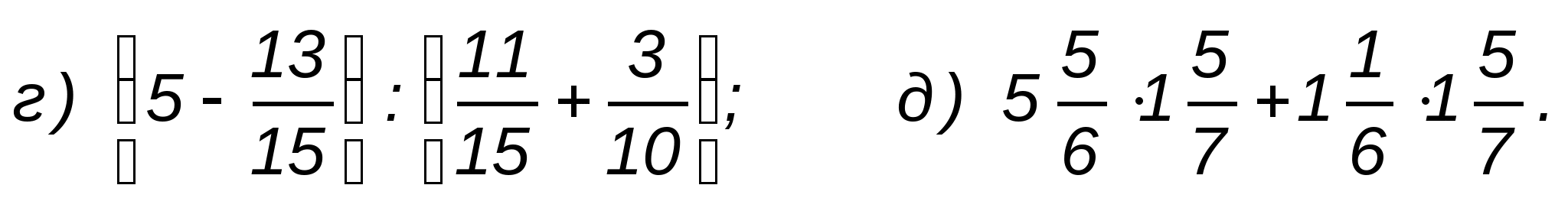
2. Решите уравнения:
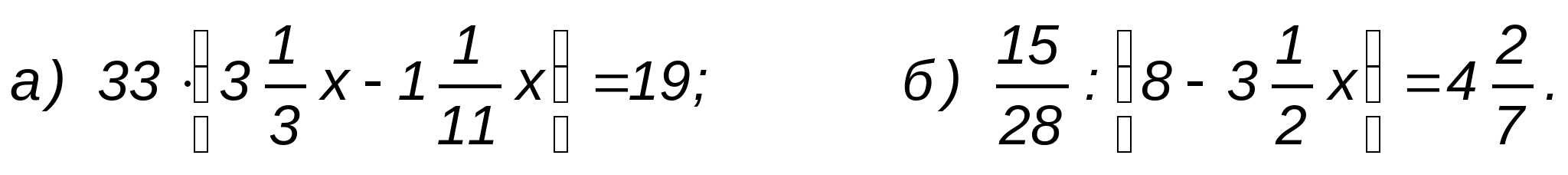
3. На складе было 1300 коробок стирального порошка. За первую неделю израсходовали 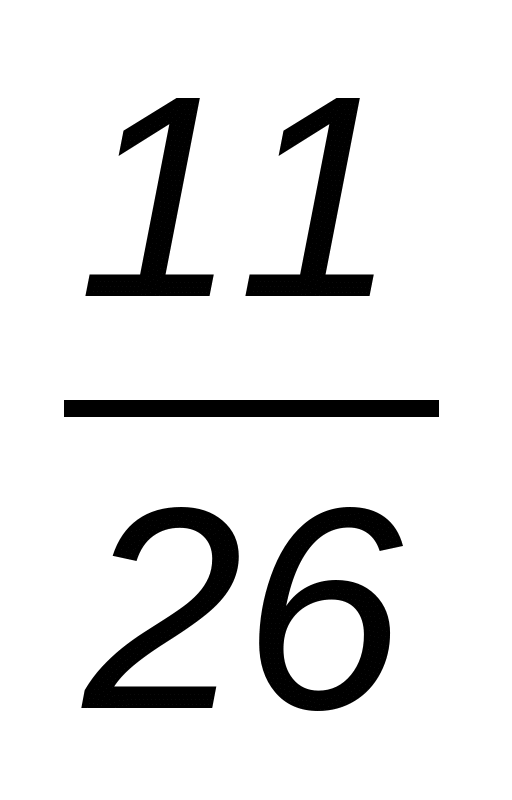 всего порошка, а за вторую —
всего порошка, а за вторую — 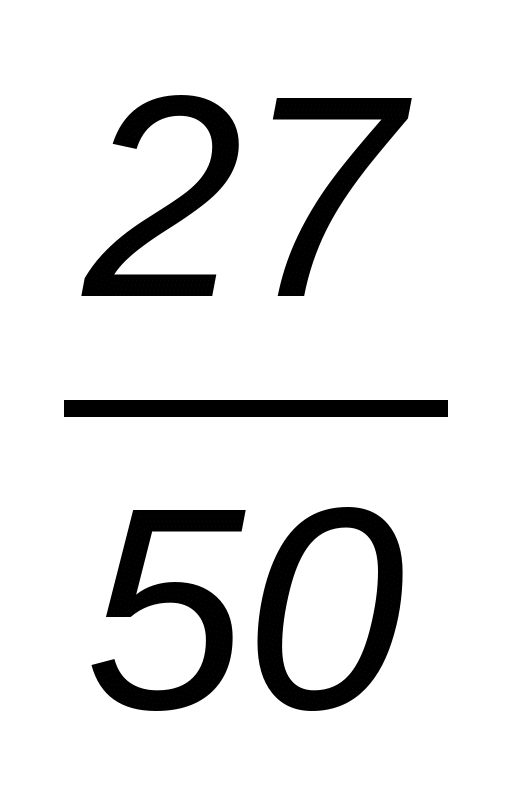 остатка. Сколько порошка израсходовали во вторую неделю?
остатка. Сколько порошка израсходовали во вторую неделю?
4. Ученик в первый день прочитал 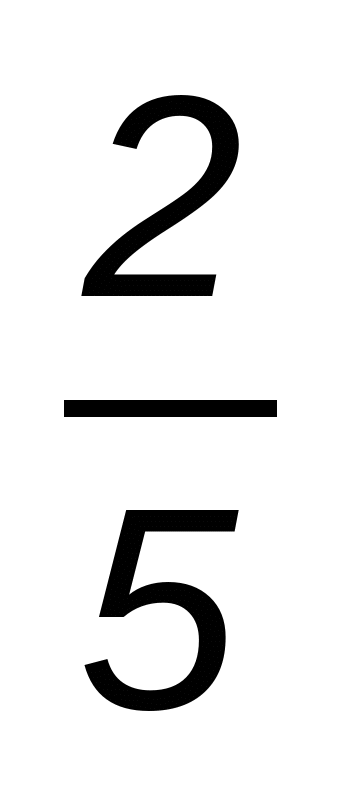 всей книги, во второй —
всей книги, во второй — 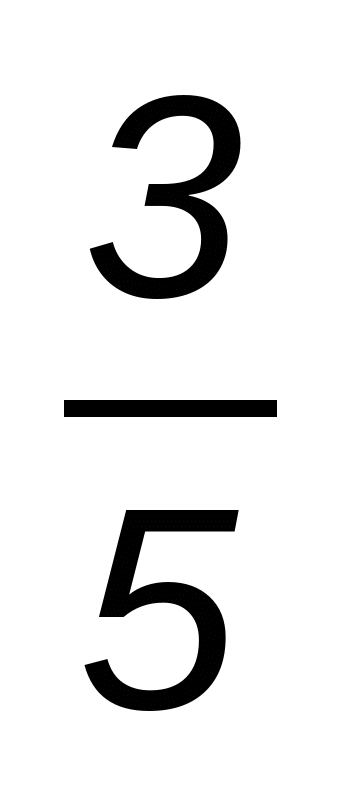 остатка, а остальные 264 страницы — в третий день. Сколько страниц в книге?
остатка, а остальные 264 страницы — в третий день. Сколько страниц в книге?
5. Первая бригада может выполнить работы по ремонту водопровода за 5 дней, а вторая — в 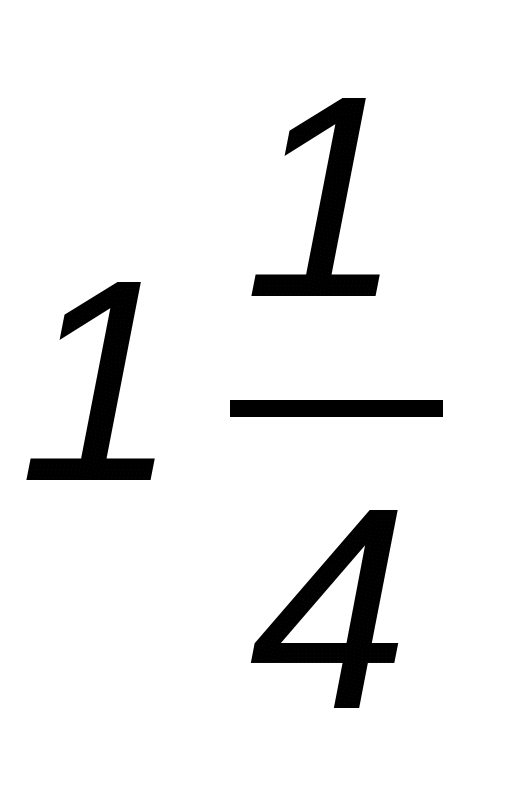 раза быстрее. Смогут ли они отремонтировать водопровод за 3 дня, если будут работать вместе?
раза быстрее. Смогут ли они отремонтировать водопровод за 3 дня, если будут работать вместе?
Дополнительное задание (оценивается отдельно):
5.4.7. Примеры на сложение и вычитание обыкновенных дробей математика-повторение
I. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Примеры.
II. Если нужно сложить дроби с разными знаменателями, то сначала дроби приводят к наименьшему общему знаменателю, а затем складывают дроби с одинаковыми знаменателями.
Примеры.
III. Чтобы выполнить вычитание дробей с одинаковыми знаменателями, из числителя первой дроби вычитают числитель второй дроби, а знаменатель оставляют тот же.
Примеры.
IV. Если нужно выполнить вычитание дробей с разными знаменателями, то их сначала приводят к общему знаменателю, а затем выполняют вычитание дробей с одинаковыми знаменателями.
Примеры.
V. При выполнении действий сложения или вычитания смешанных чисел эти действия выполняют отдельно для целых частей и для дробных частей, а затем результат записывают в виде смешанного числа.
Примеры.
Да, складывать нужно отдельно целые части и отдельно дробные части смешанного числа.
Нет, не нужно расписывать целые и дробные части смешанных чисел по отдельности.
Важно: не начинайте выполнять сложение, пока не приведете дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ).
Помним, что единицу можно представить в виде обыкновенной дроби, числитель и знаменатель которой, являются любыми равными друг другу числами.
Важно: не начинайте выполнять вычитание, пока не приведете дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ) и не убедитесь, что из числителя первой дроби можно вычесть числитель второй дроби. А если нельзя вычесть?
Тогда «занимаете» у целой части уменьшаемого одну целую единицу, представляете ее в виде неправильной дроби с таким же знаменателем (НОЗ), и добавляете эту неправильную дробь (раздробленную единицу) к дробной части уменьшаемого.
Запись имеет метки: сложение и вычитание обыкновенных дробей, сложение и вычитание смешанных чисел
Обобщающий урок по теме «Обыкновенные дроби» (5 класс)
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №276»
«Учебно-дидактические игры как средство развития познавательной активности»
Конспект урока по теме:
«Обыкновенные дроби».
( 5 класс)
Учитель математики
Куканова Ирина Анатольевна
Мурманская область
ЗАТО Александровск
г. Гаджиево
Урок «Обыкновенные дроби» — урок на повторение и закрепление пройденного материала. У этого урока нет сюжетной линии, но все задания подобраны таким образом, чтобы максимально заинтересовать учеников. Работа снова происходит в групповой форме. Это дает положительный результат, потому что у детей не сильных в математике имеется возможность несколько раз услышать и посмотреть, как выполняется то или иное задание. Кроме заданий для общего решения, есть задания для индивидуального решения. В них проявляется самостоятельность детей. Занимательно сформулированная проблема позволяет учащимся высказывать идеи, соответствующие их уровню развития.
Цели урока:
Предметные: обобщить и систематизировать знания учащихся об обыкновенных дробях, закрепить умение решать примеры и задачи на обыкновенные дроби, проверить умение работать с координатным лучом.
Личностные: развивать познавательный интерес к математике, быструю работу мысли, внимательность и смекалку; воспитывать дружеские отношения в классе и чувство сопереживания друг к другу.
Метапредметные: формировать умение самостоятельно определять учебные цели и задачи, развивать понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом, формировать умение выдвигать гипотезы при решении задач.
Планируемые результаты:
Учащийся обобщит и систематизирует знания об обыкновенных дробях, научится пошагово контролировать правильность и полноту выполнения алгоритма по повторяемой теме, закрепит навыки действий с обыкновенными дробями, научится применять приобретенные знания, умения, навыки в конкретной деятельности, самостоятельно выбирать способ решения задачи.
Материалы и оборудование урока:
Раздаточный материал (карточки с задачами, карточки тесты)
Рисунки и фотографии к заданиям
Плакат с изображением координатного луча
Набор магнитных рыбок
Плакат с высказыванием «Математика – царица наук»
Организационная структура урока:
1.Организационный этап.
Приветствие. Проверка готовности класса к уроку.
2.Актуализация опорных знаний.
Фронтальная беседа с учащимися:
Прежде чем сформулировать тему урока, учитель предлагает учащимся отгадать загадку.
Загадка: «Она бывает охотничья, барабанная и математическая». (дробь)
Учитель: «Мы заканчиваем изучение темы «Обыкновенные дроби», эта тема в курсе математики занимает одно из первых мест. Почему?».
Ученики: «Так как на протяжении всей своей жизни мы постоянно сталкиваемся с дробями. Ведь человеку нужно не только считать предметы, но и измерять величины: длины, площади, объемы, массы и т д. А величины не всегда удается измерить целыми числами».
Учитель: «А какие бы вы поставили цели и задачи нашего урока?».
Ученики: «Мы должны вспомнить и закрепить все, что знаем про обыкновенные дроби. повторить правила сложения и вычитания дробей с одинаковыми знаменателями, закрепить навыки решения задач по данному правилу».
Учитель: Чтобы наша работа не была скучной, мы будем решать какие-то задания устно, а какие-то письменно, какие-то задания будут групповыми, а какие-то индивидуальными. В конце урока вы выполните самостоятельную работу по теме «Обыкновенные дроби».
Устные упражнения.
Учитель: Начнем с устной работы. Вспомните понятие обыкновенной дроби. Я буду диктовать вам предложения, а вы должны назвать дробь, которая соответствует ответу.
Торт разрезан на 10 кусков, Оля съела 3 из них. Какую часть торта съела Оля?
В вазе лежит 13 фруктов, из них 5 бананов, 4 апельсина. Какую часть составляют бананы от всех фруктов?
Золушке высыпали 200 зерен пшена и 99 горошин. Какую часть от всех зерен составляют горошины?
У бабушки было 3 собаки и 5 попугаев. Еще ей принесли 2 котят. Какую часть составляют кошки и собаки от всех домашних животных?
К каждому заданию – рисунок.
Учитель: Теперь обратное задание. Придумайте объяснение для дроби 5/7.
Дети придумывают свои условия на заданное число.
Учитель: «Вспомним определение правильных и неправильных дробей. Поиграем в игру «Хлопушка». Я читаю дробь, вы хлопаете в ладоши, если дробь правильная: 15/17; 5/9; 20/19; 50/51; 100/200; 4/9; 75/57; 6/15; 53/23; 7/54; 3/2».
3. Основной этап
1)Решение примеров.
Учитель: Следующее задание – письменное.
Составить все правильные дроби со знаменателем 17;
Составить все неправильные дроби с числителем 15.
На выполнение задания дается 2 минуты. Двое учеников записывают дроби на доске, остальные – в тетрадях. При проверке у ребят появляется возможность добавить дроби или исправить их.
Учитель: «Итак, мы с вами вспомнили, что означает дробь, какие дроби бывают. А сейчас мы вспомним правила перевода неправильных дробей в смешанные числа и наоборот, смешанных чисел в неправильные дроби».
На каждую парту дается карточка, на которой есть неправильные дроби и смешанные числа. На выполнение данного задания дается максимально 3 минуты.
Учитель: «Когда все будут готовы, мы будем создавать кораблики. Лодки для корабликов со знаменателем на борту уже есть на карточках. Ваша задача – правильно подобрать паруса. К знаменателю подбирается числитель из получившихся дробей. А у смешанных чисел целую часть показывает флажок на палочке».
Если кораблик составлен неверно, то его исправляют участники из других групп. На карточке записать три неправильные дроби и три смешанных числа: 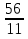 ;
; 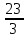 ;
; 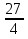 ; 2
; 2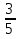 ; 5
; 5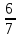 ;
;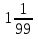 .
.
7
41
11
1
5
13
5



99
100
3
2
7
4
3
6



Класс делится на 4-5 команд.
Учитель: Следующее задание займет очень мало времени, но будет показательным. Оно покажет, умеете ли вы складывать и вычитать дроби, и то, как от одной ошибки зависит результат всего класса. На доске зашифрована фраза, вам ее нужно отгадать. На доске записаны примеры для каждого ряда. Вы по очереди решаете задания из своего столбика, а затем возвращаетесь назад, отдав мел следующему члену своей команды. Затем все вместе по таблице с алфавитом мы расшифруем предложение. Вывешивается плакат. Должно получится: « Математика – царица наук».
 +
+ 
5) 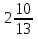 —
— 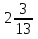
9)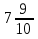 —
— 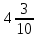
13)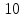 —
— 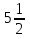
17)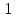 +
+ 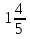
 +
+ 
6)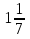 +
+ 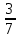
10)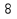 —
— 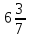
14)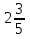 +
+ 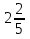
18)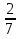 +
+ 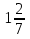
 —
— 
7)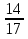 —
— 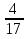
11)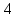 —
— 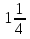
15)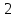 +
+ 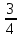
19)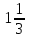 +
+ 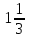
 +
+ 
8) 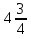 +
+ 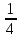
13)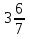 —
— 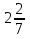
16)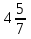 —
— 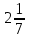
20)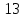 —
— 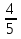
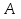 —
— 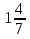
Е — 10
Л — 3
Р — 4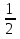
Х — 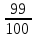
Ь, Ъ — 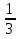
Б — 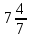
Ж — 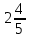
М — 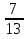
С — 11
Ц — 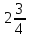
Ы — 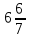
В — 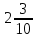
З — 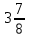
Н — 2 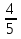
Т — 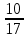
Ч — 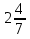
Э — 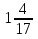
Г- 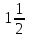
И, Й — 5
О -3 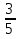
У — 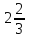
Ш — 1
Ю — 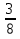
Д — 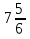
К+ 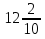
П — 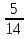
Ф — 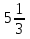
Щ — 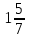
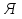 — 9
— 9 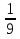
2)Решение задач.
Учитель: А сейчас мы приступим к решению задач. Раздаются карточки, и после 4 минут решения начинается обсуждение. Чтобы успеть обсудить и записать все задачи, нужно экономить время. Для этого пока один ученик объясняет решение, кто-то другой готовит запись на доске. При раздаче карточек нужно обратить внимание, что с 1 по 4 задания задачи усложняются.
Расстояние от села до города 15 км. Путник прошел
 этого расстояния. Сколько километров осталось ему пройти?
этого расстояния. Сколько километров осталось ему пройти?
В коробке находилось 24 мяча. Красные мячи составляли
 мячей, а зеленые –
мячей, а зеленые –  оставшихся мячей. Сколько было зеленых мячей?
оставшихся мячей. Сколько было зеленых мячей?
Отремонтировали 80 тракторов, что составляет
 всех тракторов. Сколько всего было тракторов?
всех тракторов. Сколько всего было тракторов?
В бензобаке автомашины был бензин. Перед поездкой в него налили еще 10 литров бензина. За время поездки была истрачена
 часть находившегося в баке бензина. Сколько бензина было в бензобаке первоначально, если во время поездки было истрачено 12 литров?
часть находившегося в баке бензина. Сколько бензина было в бензобаке первоначально, если во время поездки было истрачено 12 литров?
3) Работа на числовом луче. «Математическая рыбалка».
Учитель: Теперь мы перейдем к работе на координатном луче. Это задание в некотором смысле творческое и потребует от вас не только знаний, но и сообразительности. На нашем плакате четыре рыбки, нужно назвать точную координату каждой рыбки как можно большим количеством способов. Для этого даются длина единичного отрезка – 30 см и расстояние до каждой рыбки. На обсуждение – 4 минуты. Если три координаты являются верными, то рыбка считается пойманной. Дети должны сообразить, что единичный отрезок можно изначально разделить на число, а уже затем составлять дробь. Например, для 6 см единичный отрезок можно разделить на 30 см; на 6см; на 3см, и получатся дроби: 6/30; 1/5; 2/10.
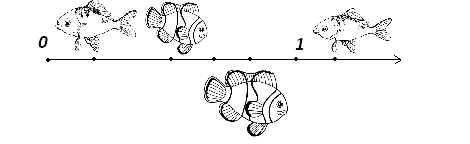
4) Тесты по вариантам ( 8-10 минут).
Вариант 1
№1. Выберите из данных дробей те, которые обозначают половину: 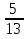 ,
, 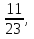
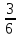 ,
, 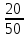 ,
, 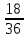 .
.
№2. Сравните дроби: а) 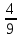
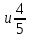 ; б)
; б)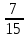
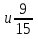 ;
;
в) 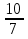
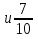 .
.
№3. При каких натуральных значениях х дробь 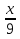 правильная?
правильная?
№4. Решите уравнение: 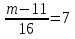 .
.
№5*. На вопрос “Который час?” ответили, что оставшаяся часть суток равна 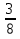 целых суток. Который был час?
целых суток. Который был час?
Вариант 2
№1. Выберите из данных дробей те, которые обозначают половину: 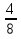 ,
, 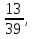
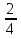 ,
, 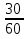 ,
, 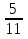 .
.
№2. Сравните дроби: а) 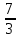
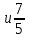 ; б)
; б)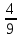
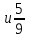 ;
;
в) 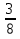
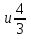 .
.
№3. При каких натуральных значениях х дробь 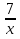 неправильная?
неправильная?
№4. Решите уравнение: 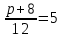 .
.
№5*. Стеклянная бутылка с водой весит 550 г. Когда из бутылки вылили 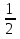 всей воды, ее масса составляла 300 г. Сколько грамм воды было в бутылке сначала?
всей воды, ее масса составляла 300 г. Сколько грамм воды было в бутылке сначала?
4.Рефлексия.
Учащиеся оценивают свою работу, выбирая карточку самооценки, и показывают её:
— Я работал(а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно (красная карточка)
— Я работал(а) хорошо, но не в полную силу, испытывал(а) чувство неуверенности, боязни, что отвечу неправильно (зелёная карточка).
— У меня не было желания работать. Сегодня не мой день ( синяя карточка).
5. Информация о домашнем задании.
Учитель дает пояснения по дифференцированному домашнему заданию:
1 уровень: составить задания для соседа по парте на различные действия с обыкновенными дробями (сложение и вычитание) по 4 примера.
2 уровень: найти в справочном материале историческую справку по теме.
3 уровень: написать сочинение на тему: «Обыкновенные дроби».
6. Подведение итогов.
Учитель благодарит ребят за интересную работу, хорошие отметки, прекрасное настроение и отличные знания.
Список используемых источников и литературы:
1. Конструирование современного урока математики / Манвелов С. Г. –М.: Просвещение 2005 г.
2. Математика: 5 класс: дидактические материалы: сборник задач и контрольных работ / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2013.
3. Математика: 5 класс: рабочая тетрадь №1, №2 / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2013.
4. Математика: 5 класс: методическое пособие / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2013.
5. Математика. Предметное портфолио пятиклассника. Самооценка. Самоанализ. Самоконтроль / Т.Ю. Дюмина, А.А.Махонина – Волгоград: Учитель,2013.
6. Математика 5 класс. Тетрадь 1,2 .Задания для обучения и развития учащихся./ Беленкова Е.Ю., Лебединцева Е.А. – М: Интеллект- Центр, 2013
7. Сборник практических задач по математике: 5 класс / Л.П. Попова . – М.: ВАКО, 2012. .
тренажер 5 класс по теме: «Обыкновенные дроби»
Карточки-тренажеры
Карточки-тренажеры можно использовать как обучающие, ликвидации пробелов знаний по теме «Обыкновенные дроби».
Сравнение, сложение и вычитание дробей с одинаковыми знаменателями.
Сравнивай, складывай, вычитай числители.
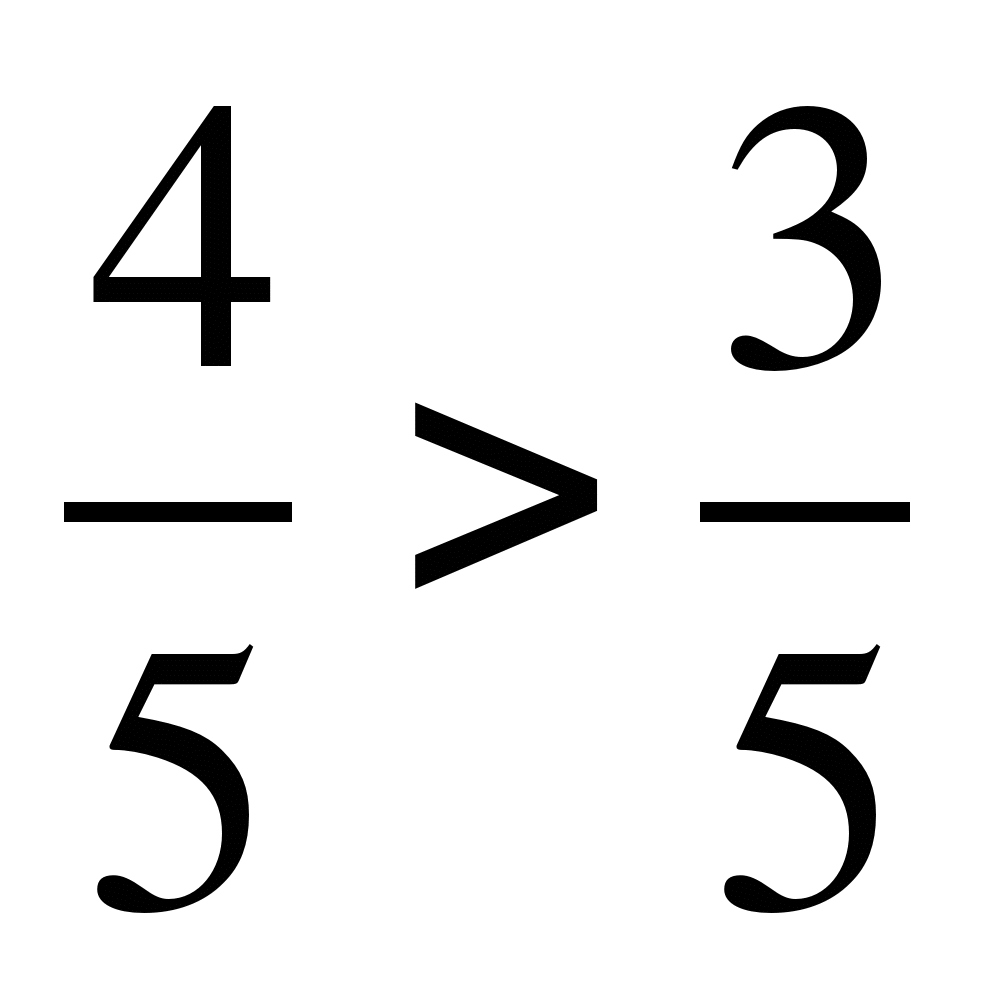 , так как
, так как
4 > 3.
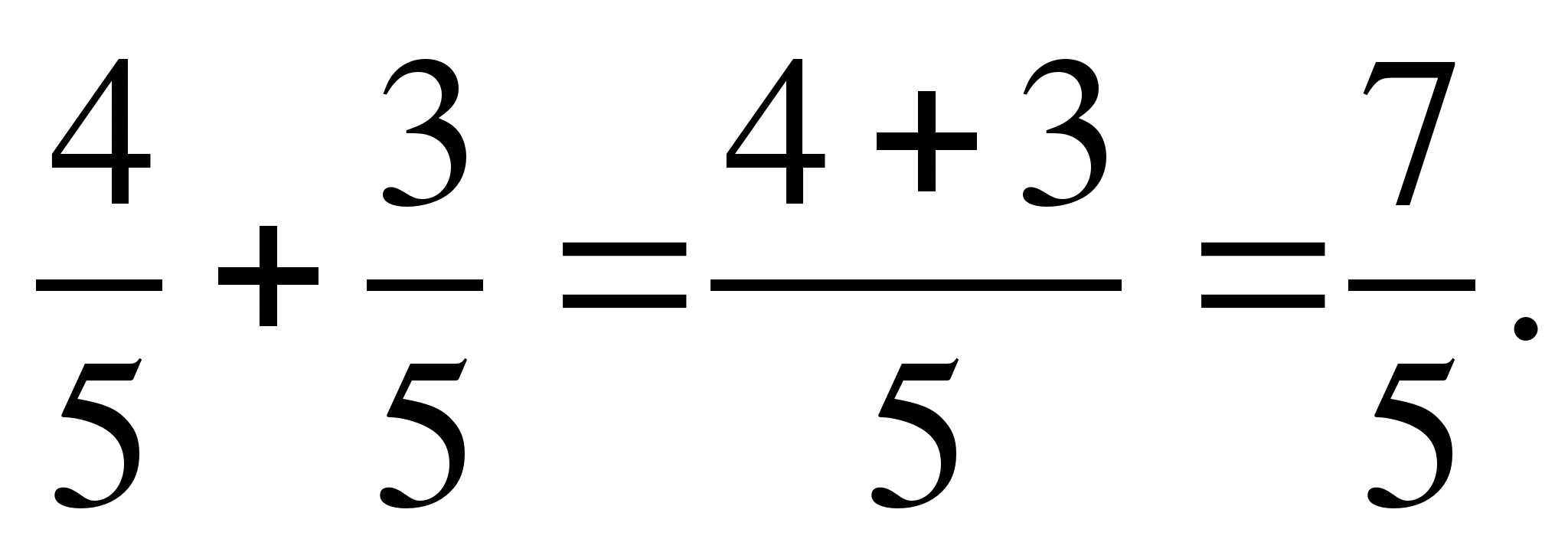
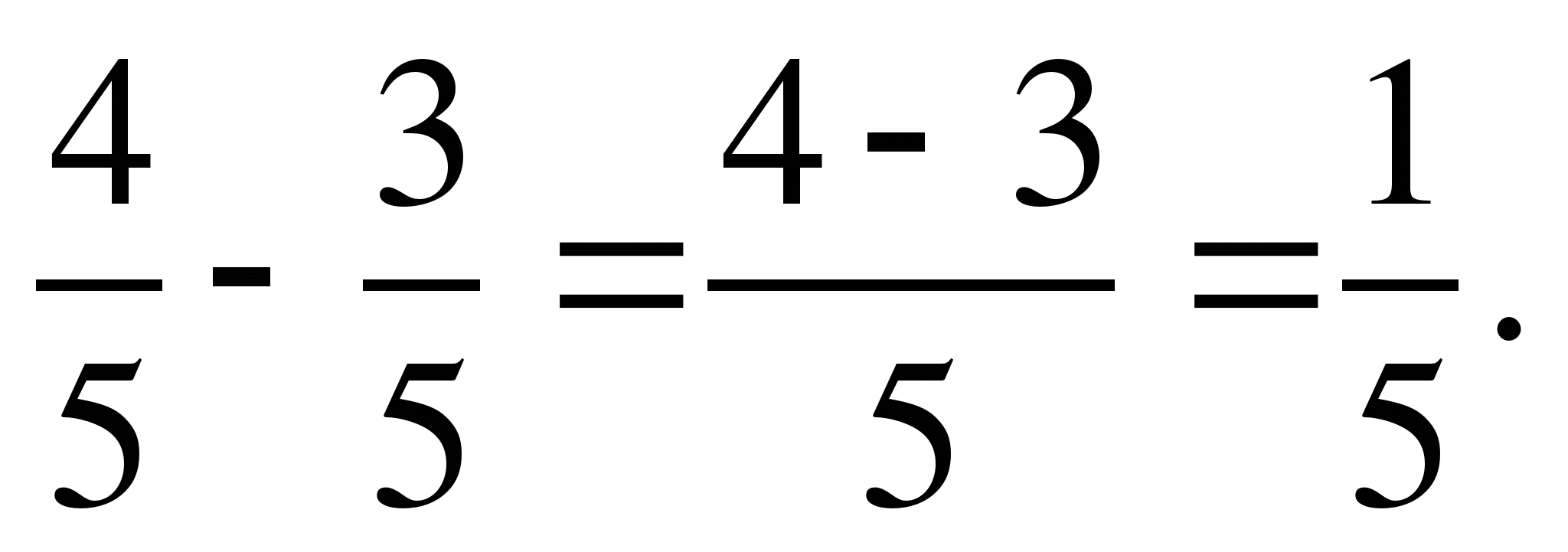
Сравнить числа, найти их сумму и разность:
1)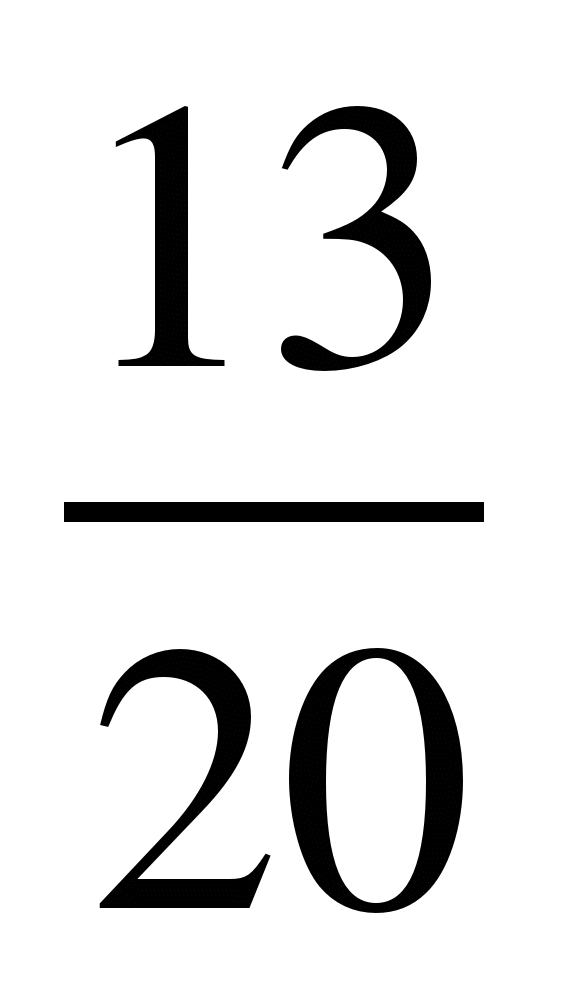 и
и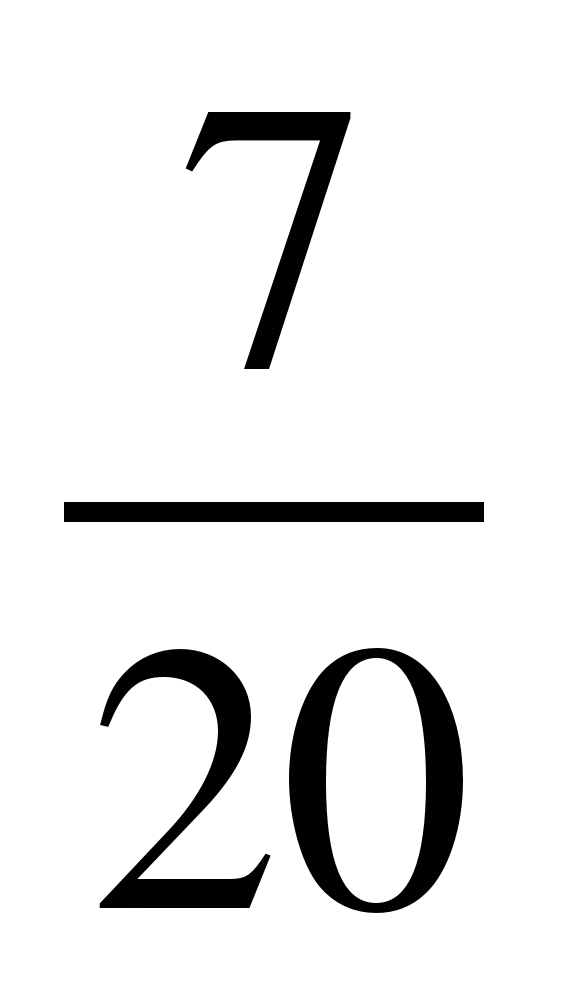 ; 2)
; 2)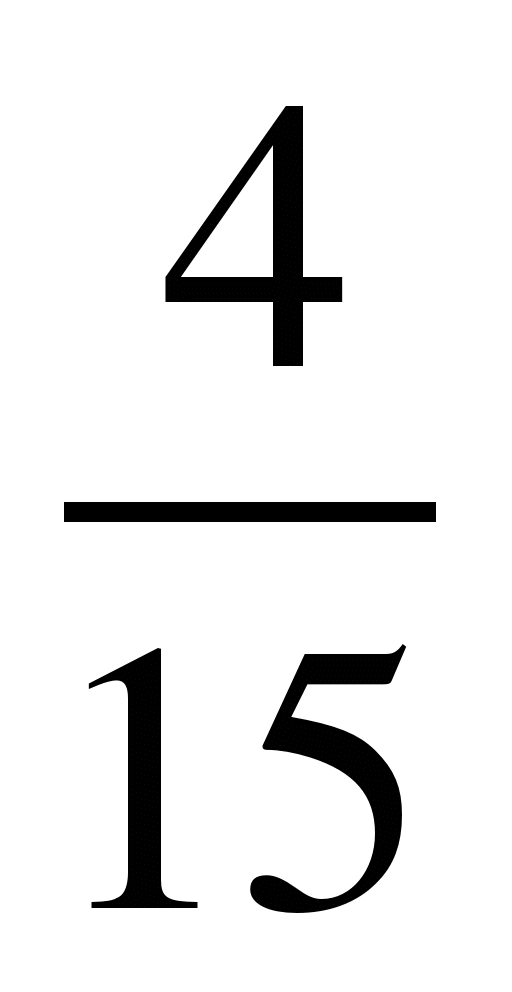 и
и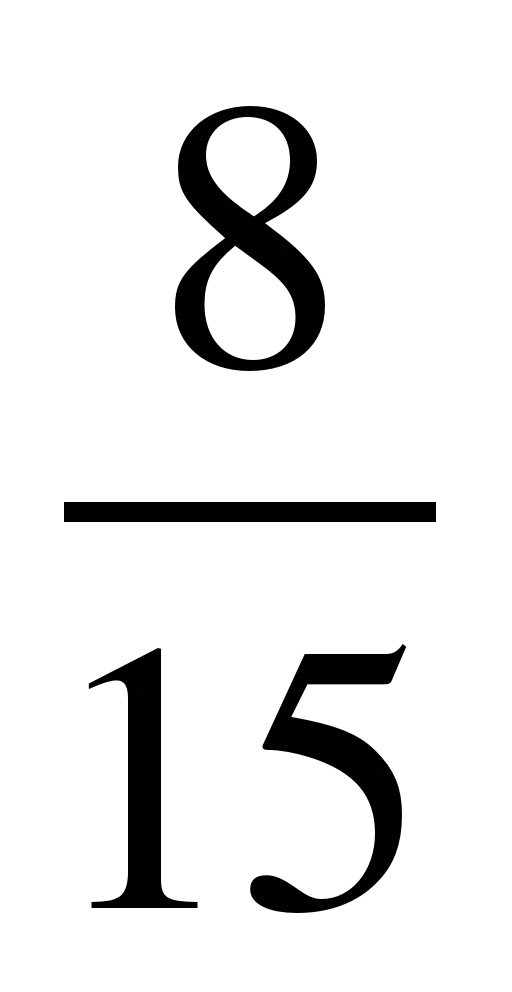 ; 3)
; 3)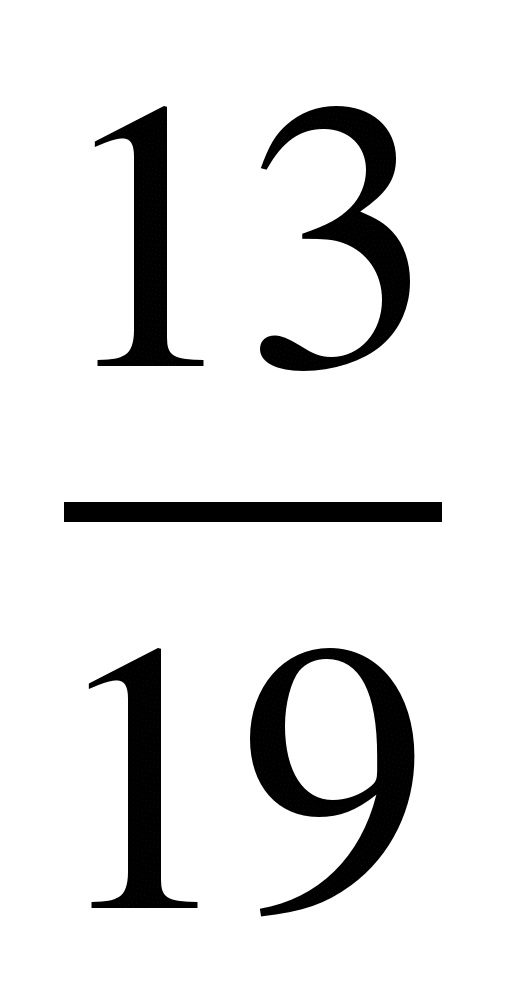 и
и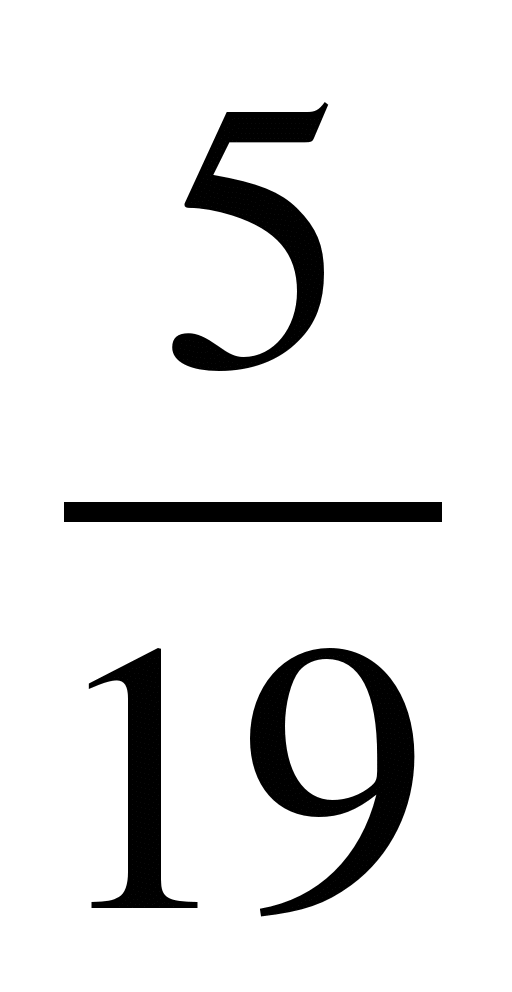 ;
;
4)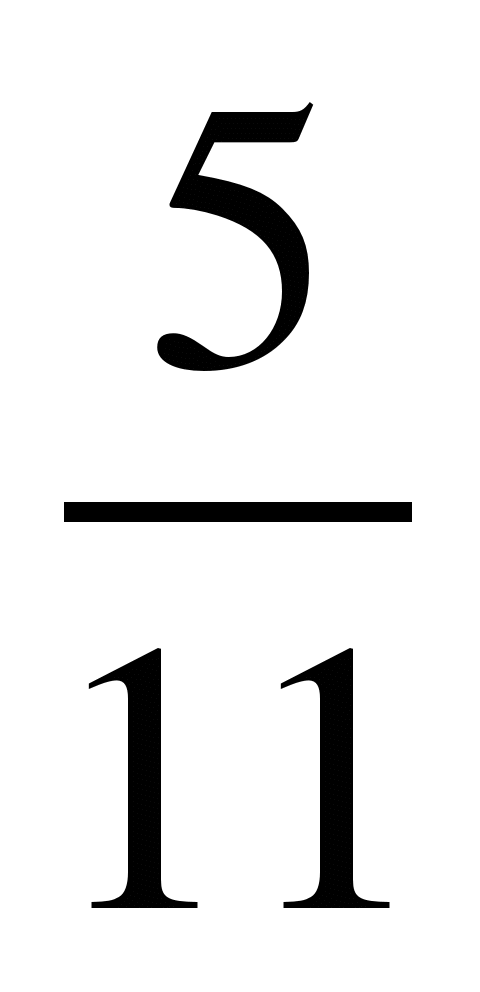 и
и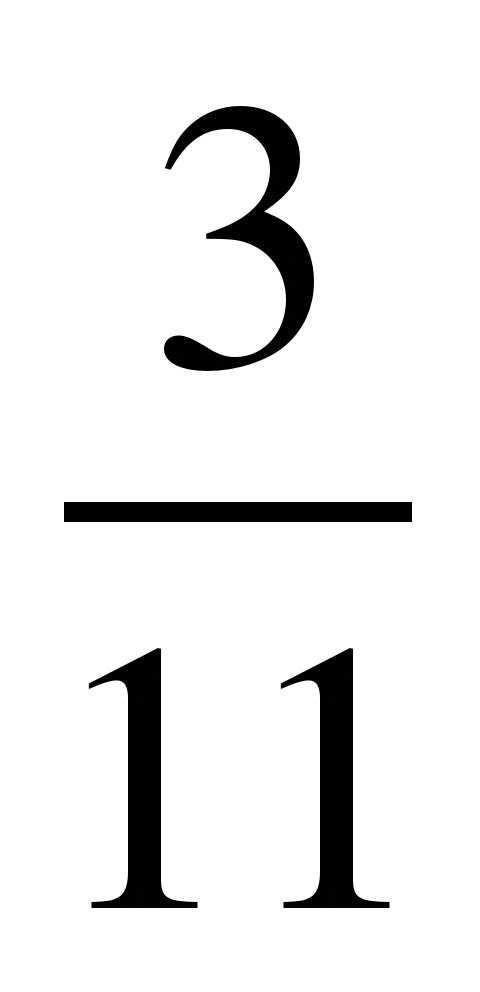 ; 5)
; 5)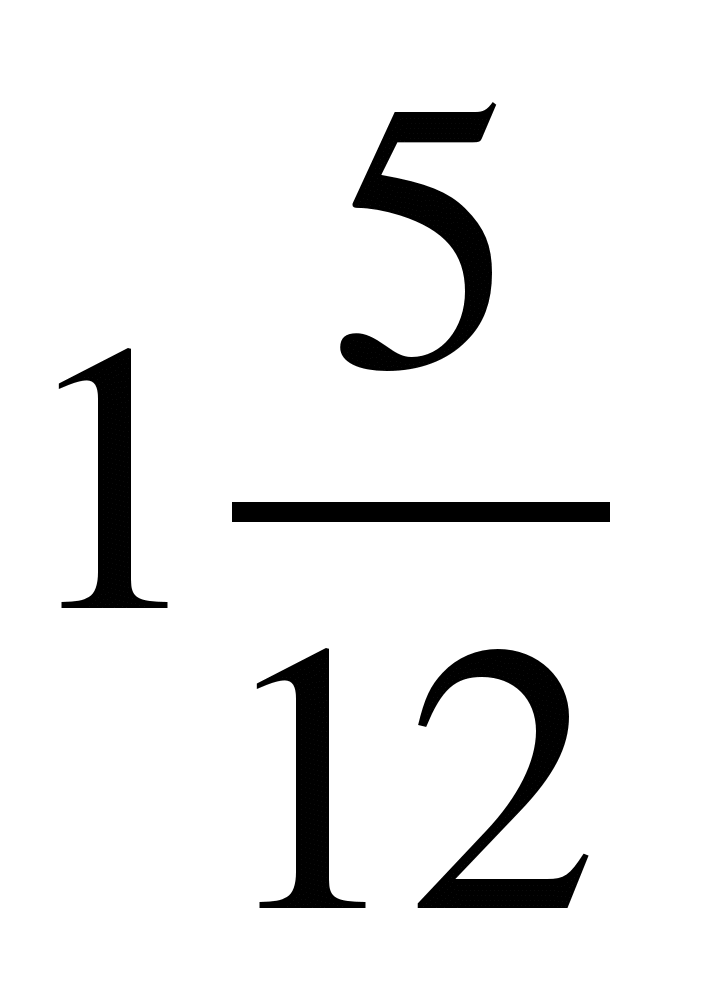 и
и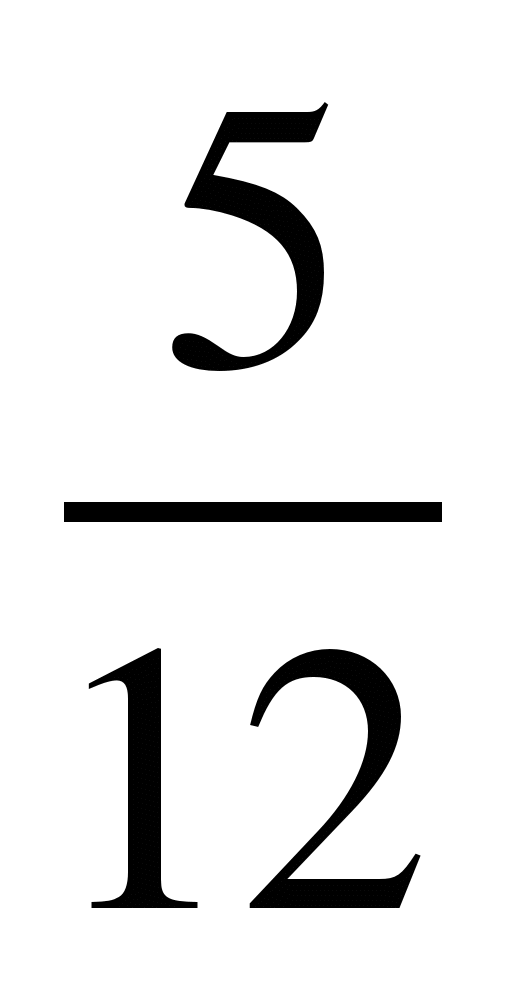 ; 6)
; 6)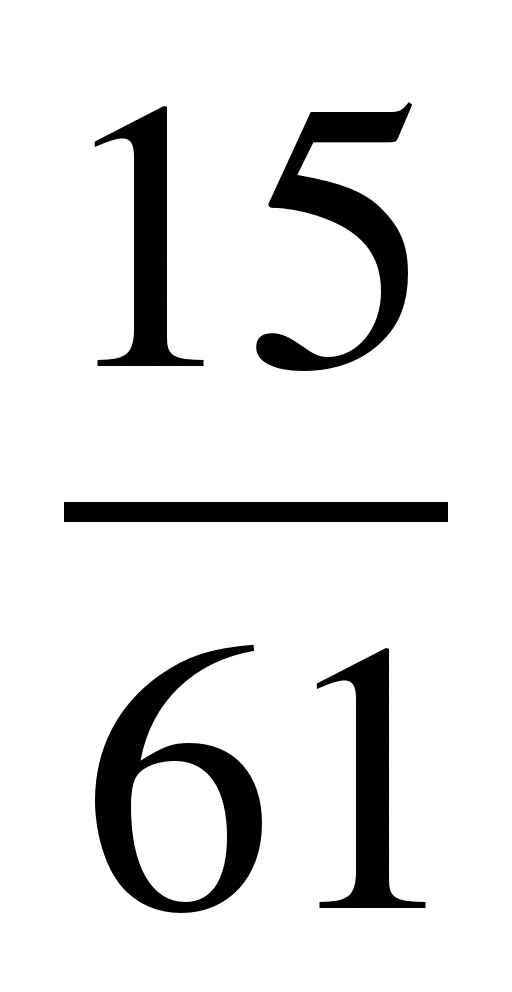 и
и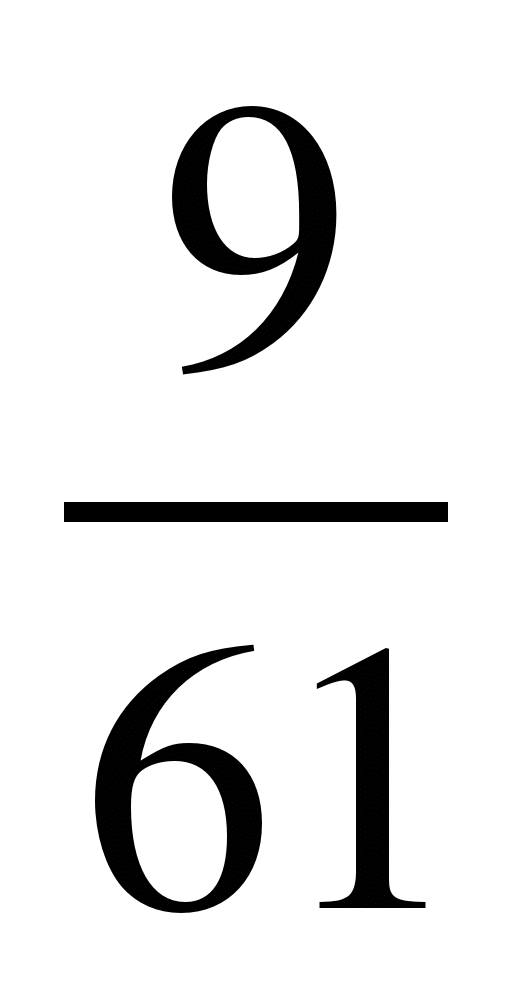 ;
;
7)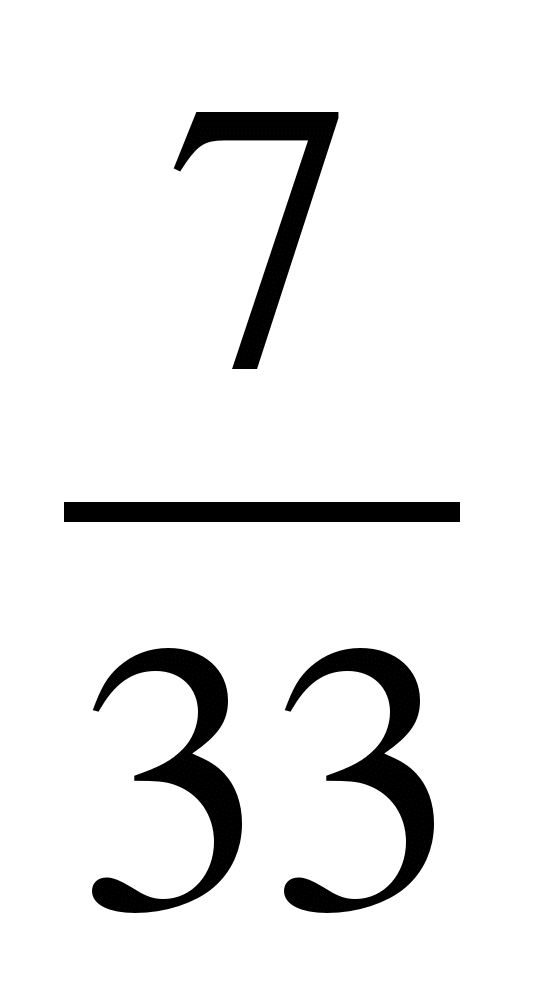 и
и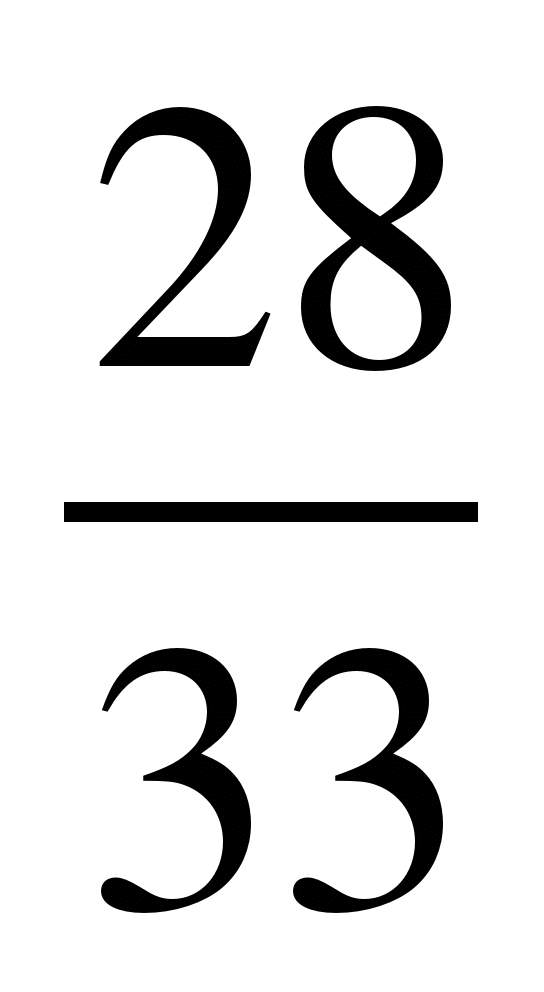 ; 8)
; 8)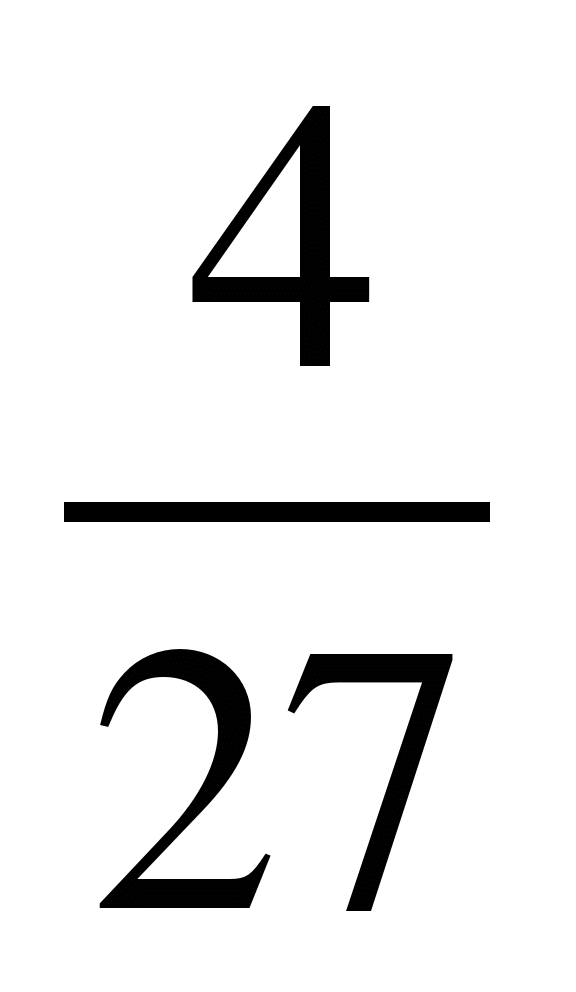 и
и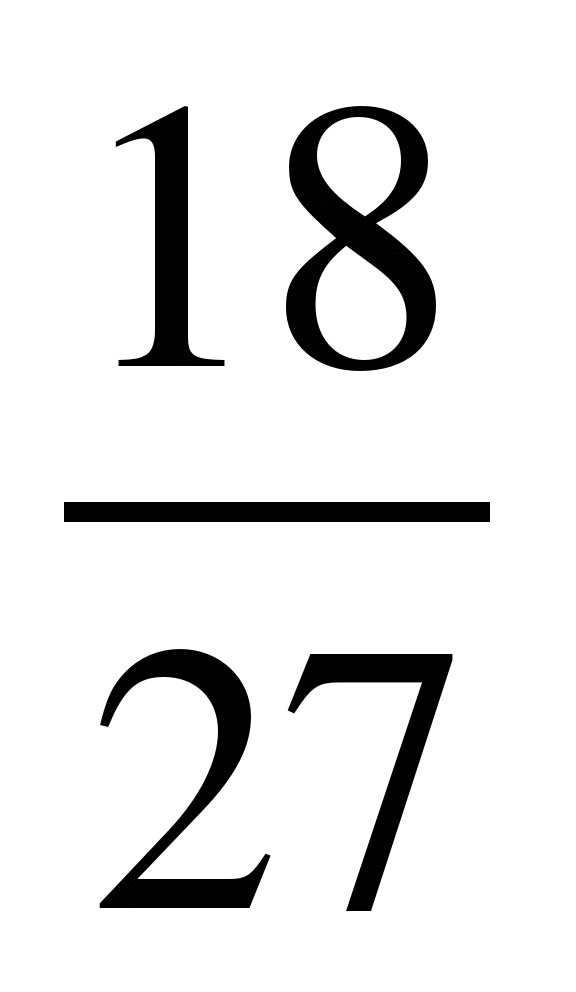 ; 9)
; 9)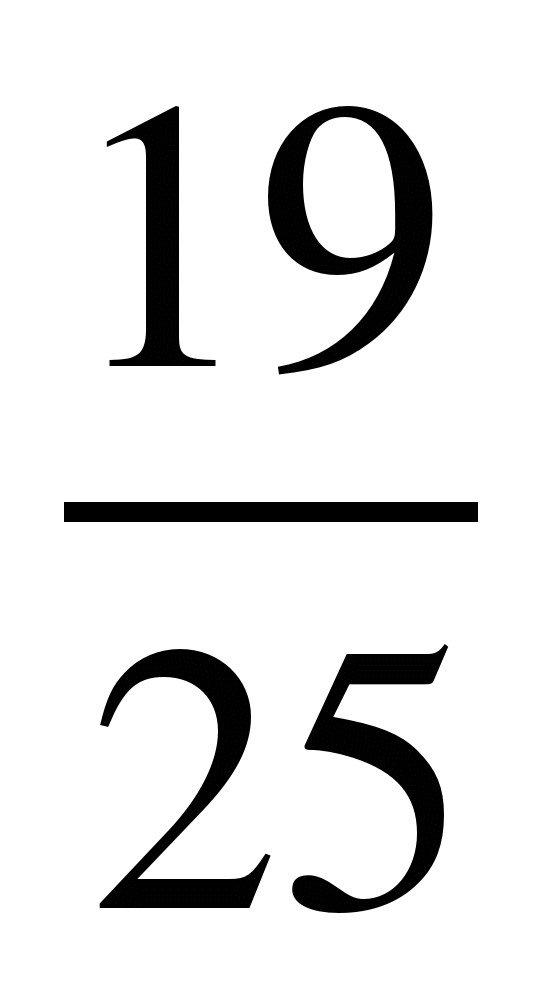 и
и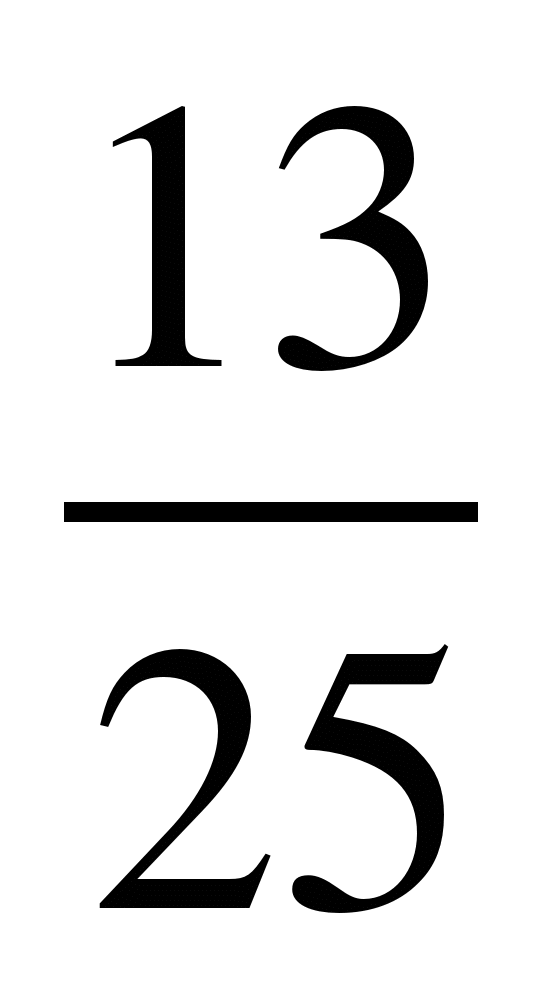 ;
;
10)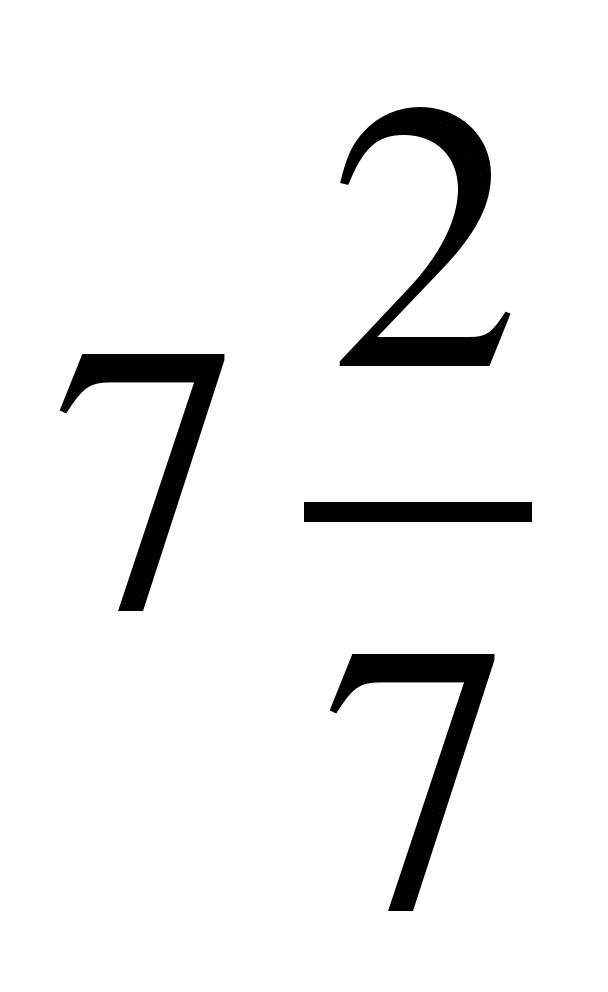 и
и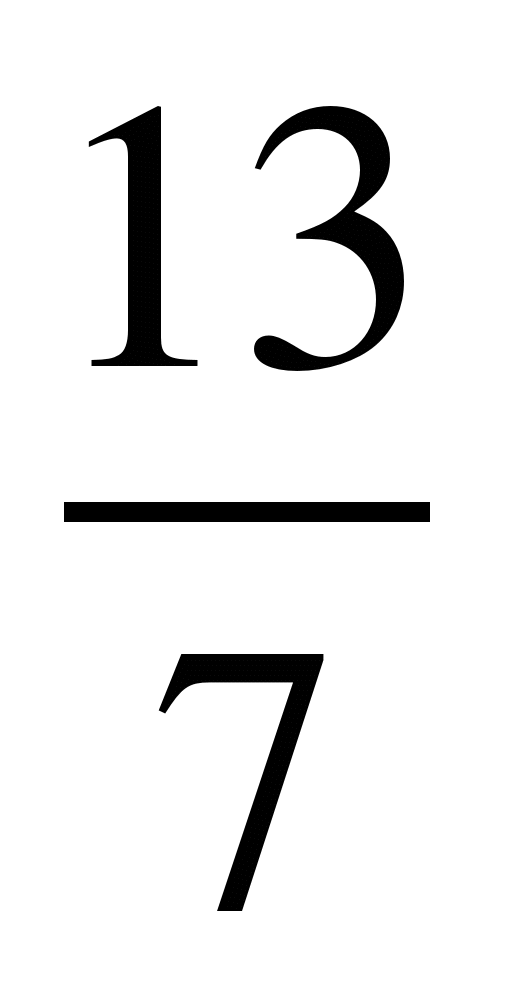 ; 11)
; 11)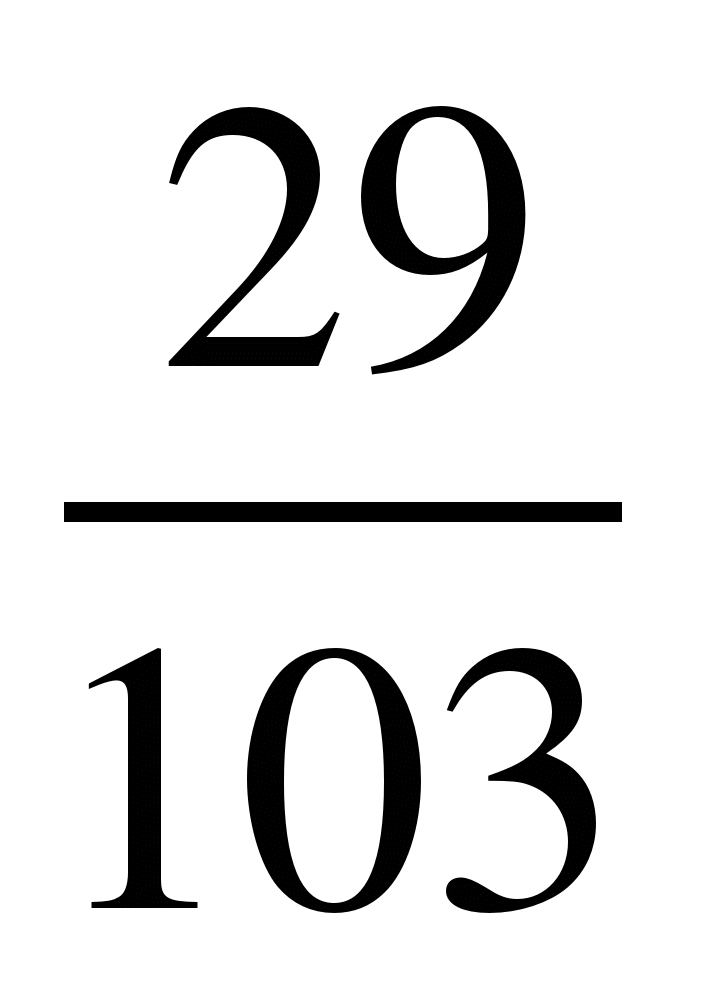 и
и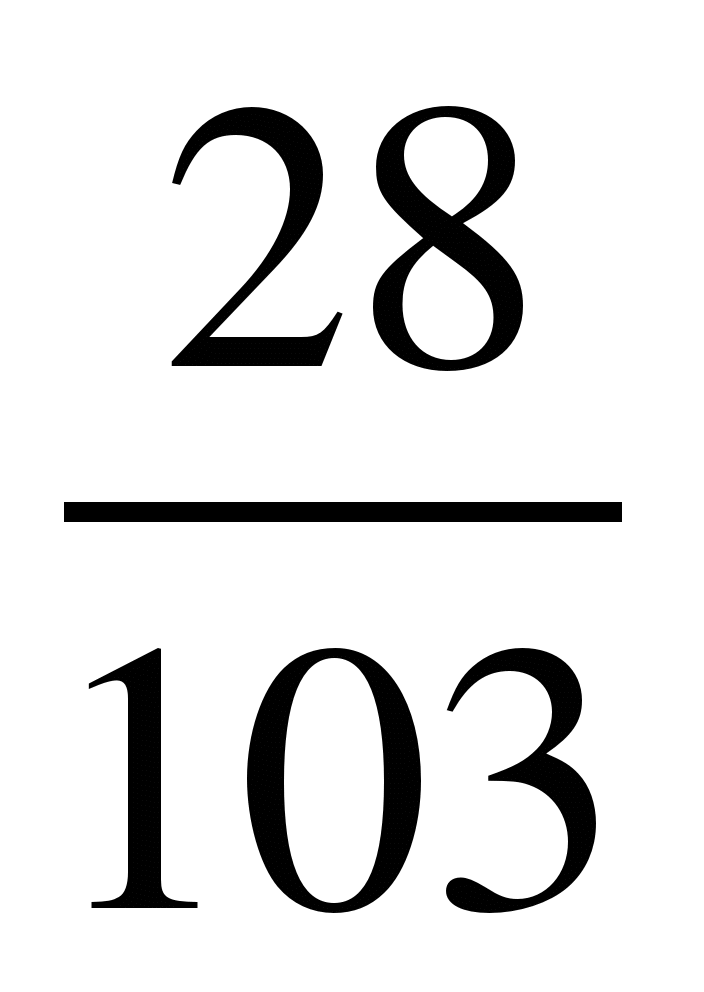 ; 12)
; 12)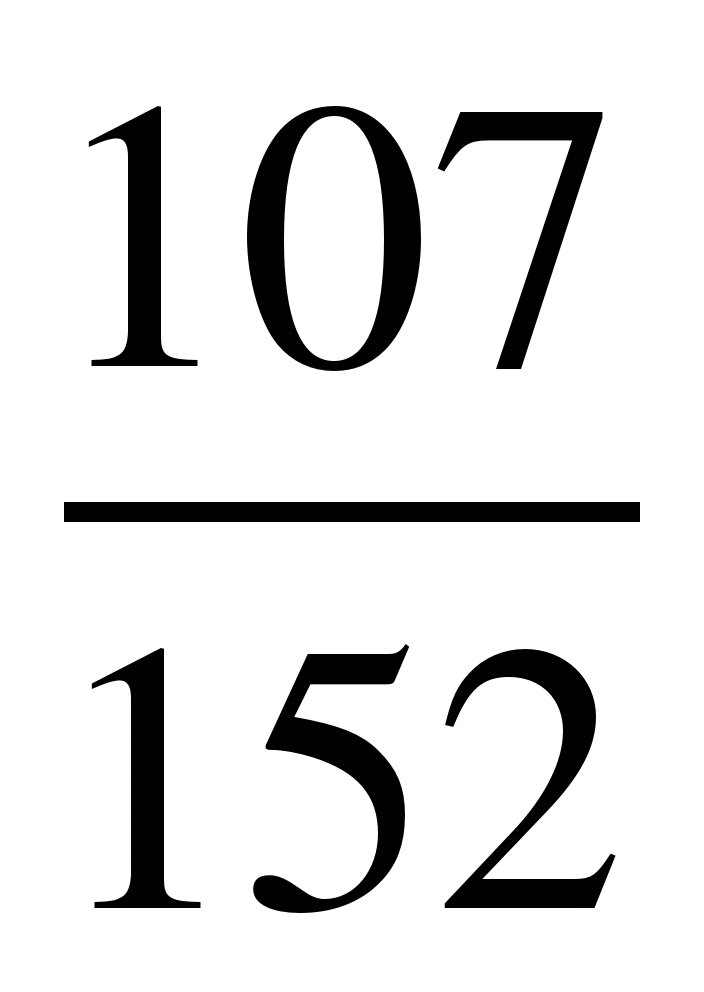 и
и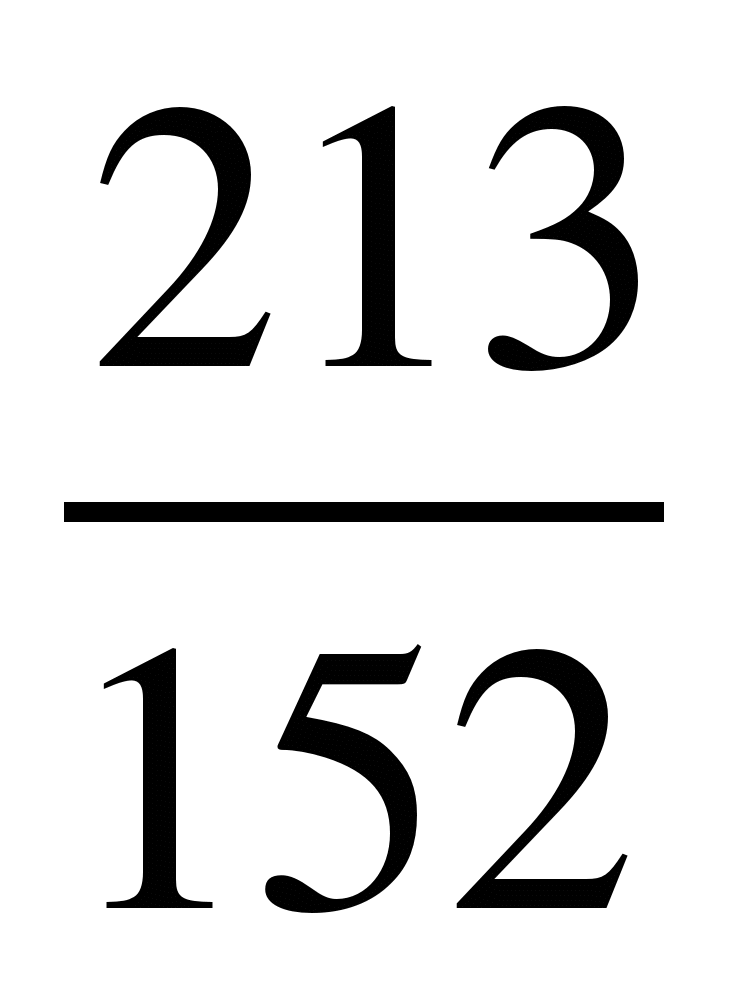 ;
;
13)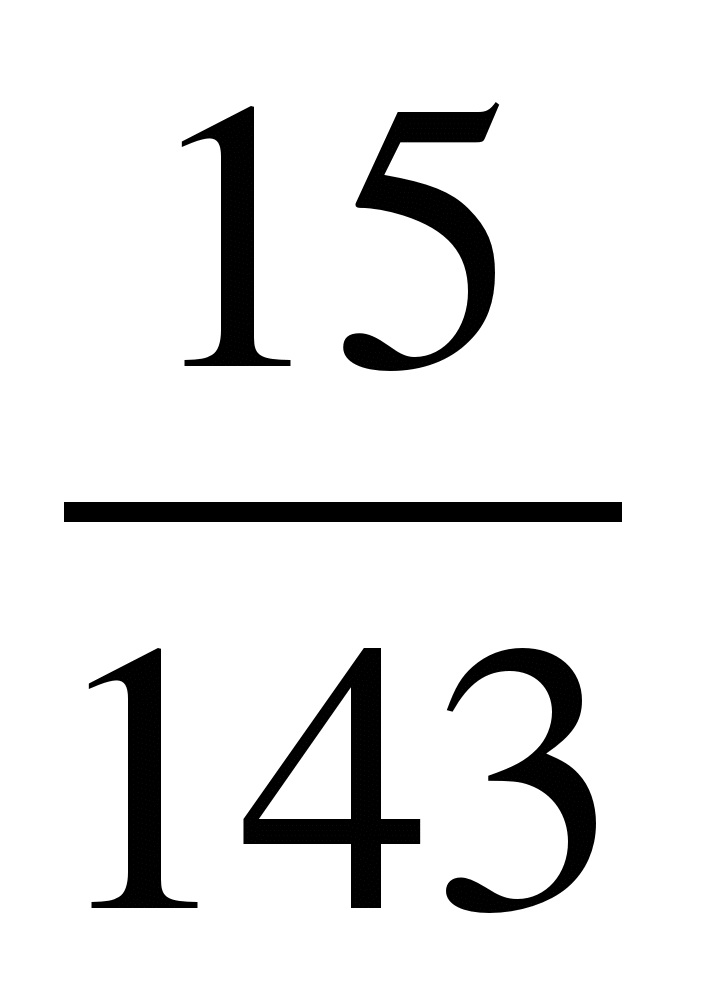 и
и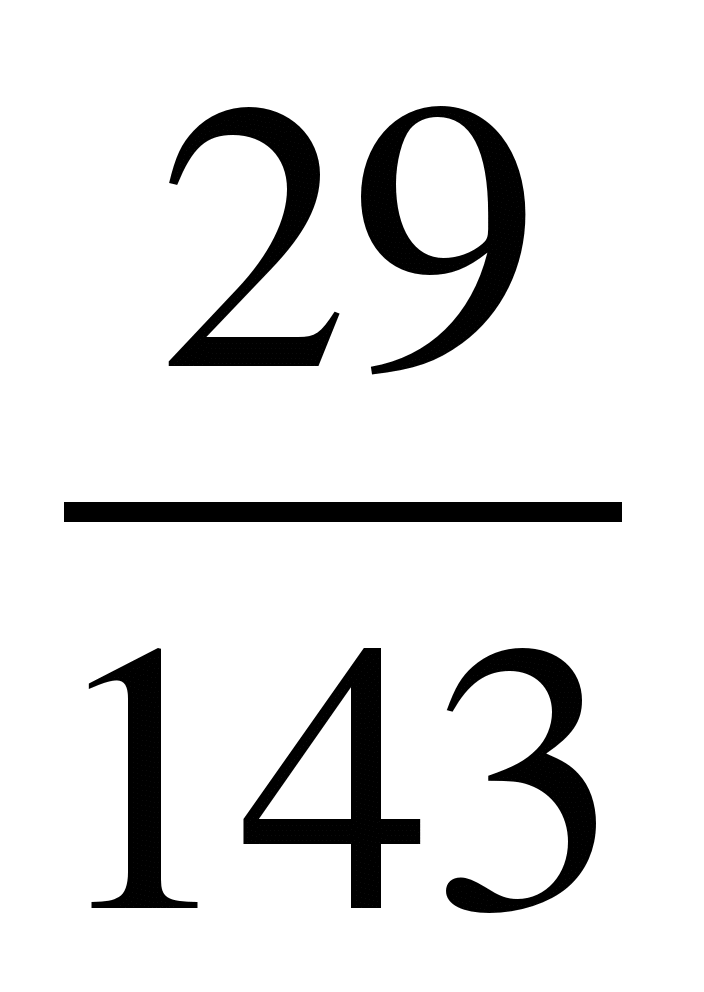 ; 14)
; 14)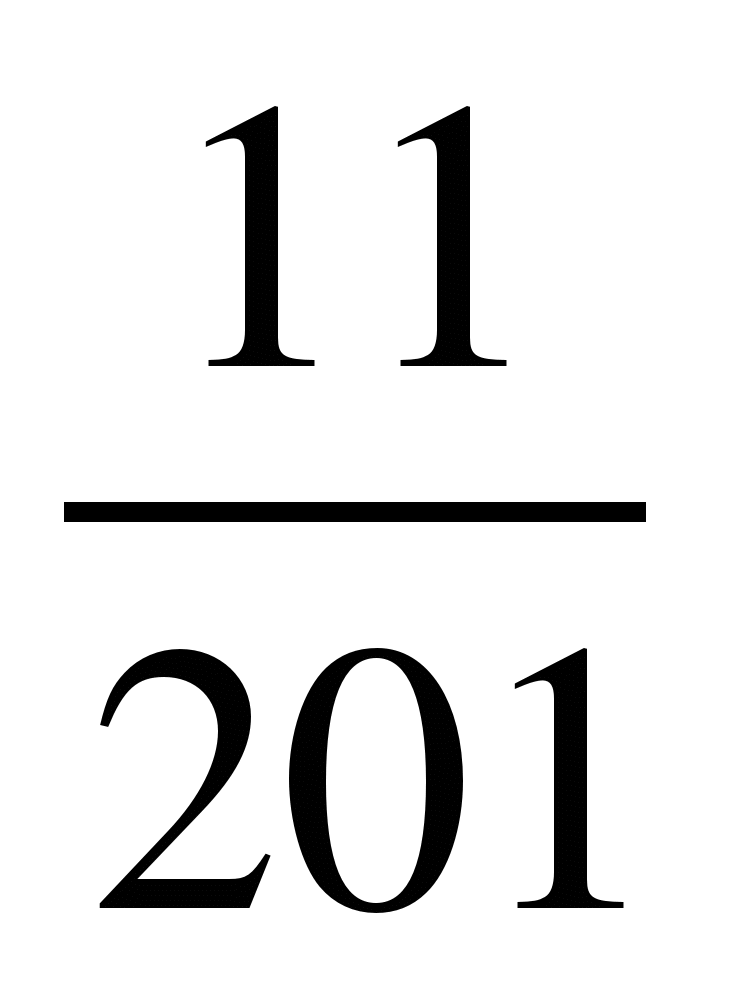 и
и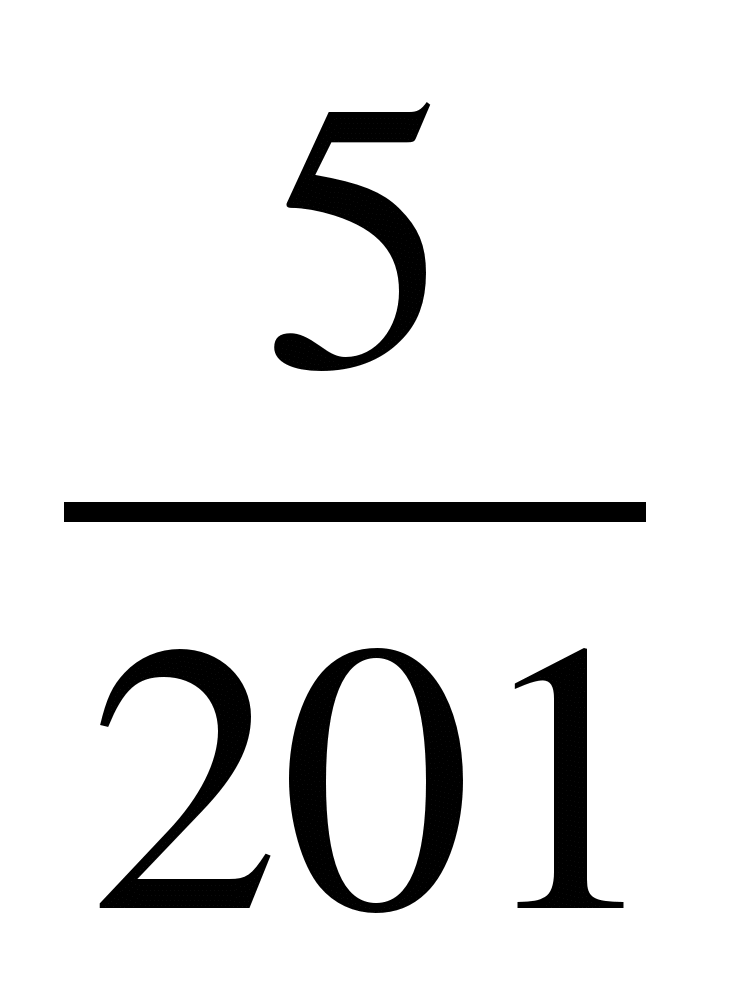 ; 15)
; 15)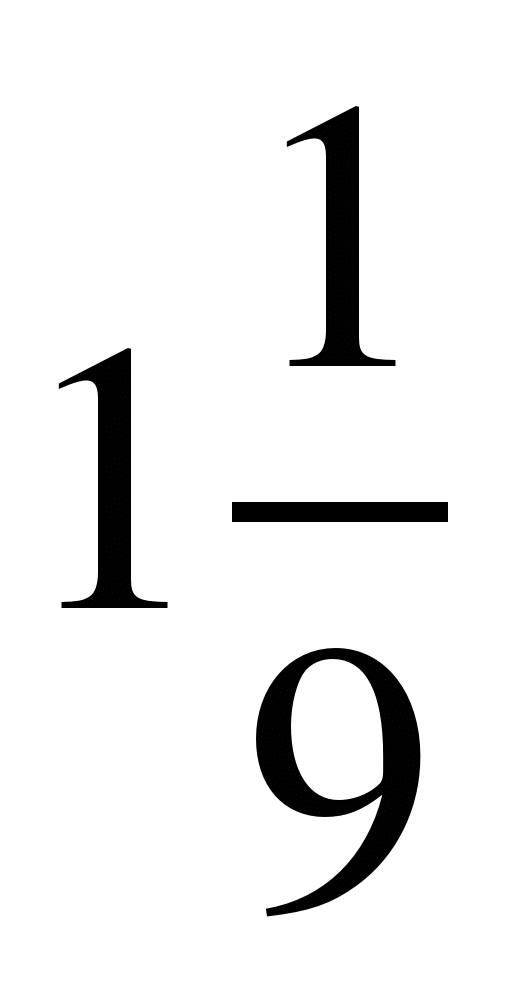 и
и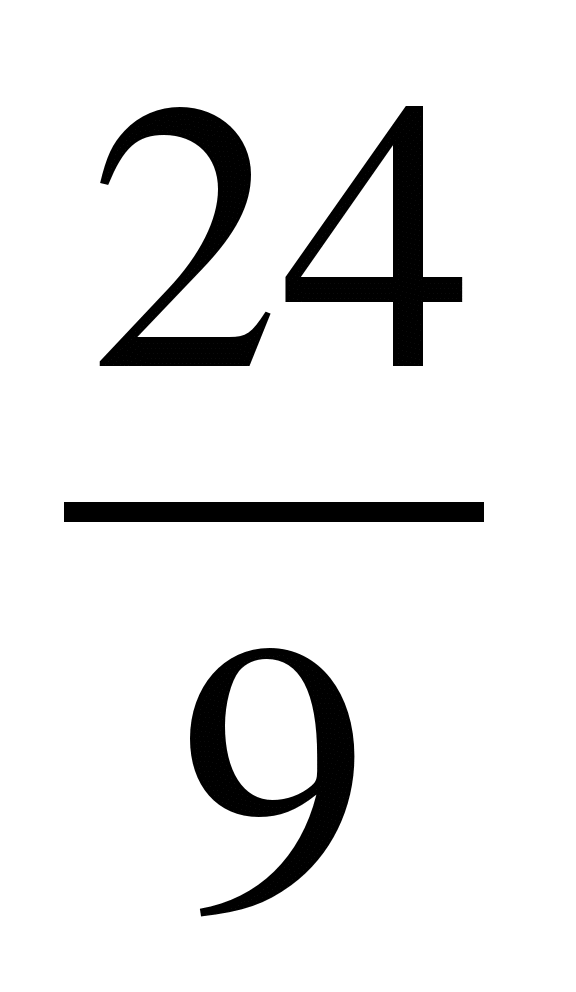 .
.
Основное свойство дроби.
Приведение дроби к новому знаменателю:
1.Умножь (или раздели) знаменатель дроби на число.
2.Умножь (или раздели) числитель дроби на то же число.
3.Запиши в ответе получившуюся дробь.
Привести дробь 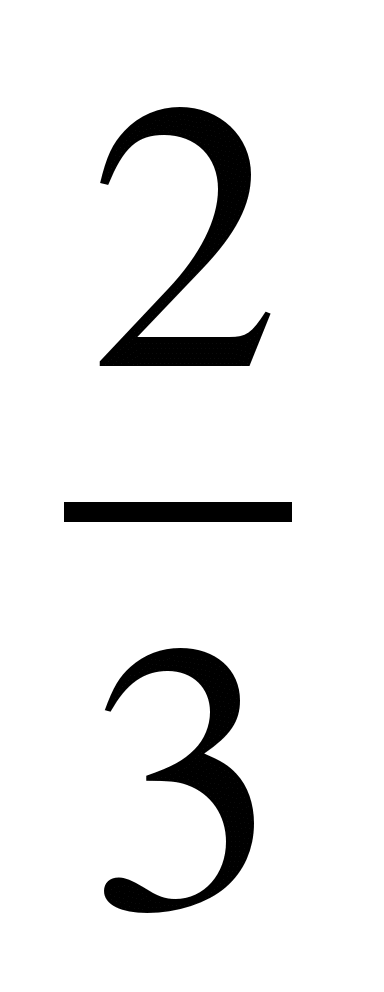 к знаменателю 15.
к знаменателю 15.
Решение.
1) 3 5 = 15;
2) 2 5 = 10;
3) Ответ: 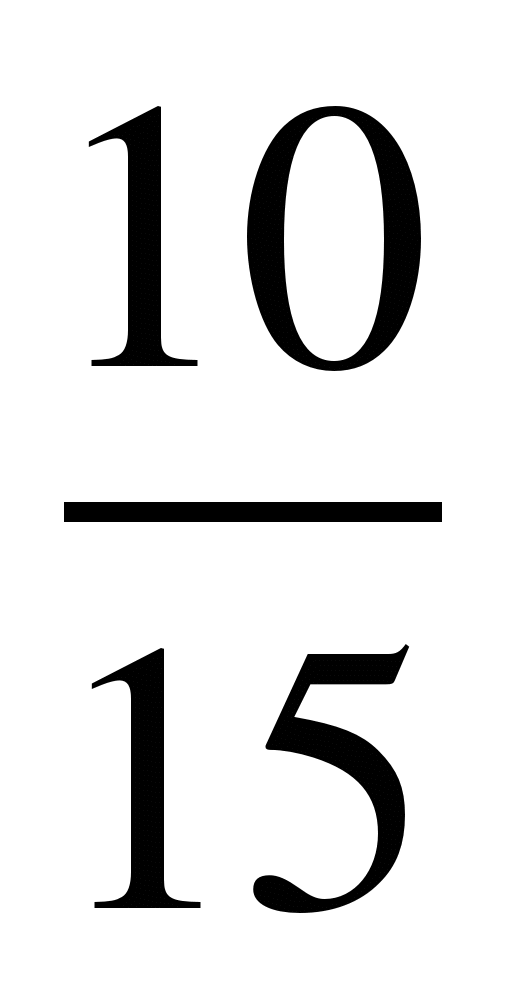 .
.
Привести дробь 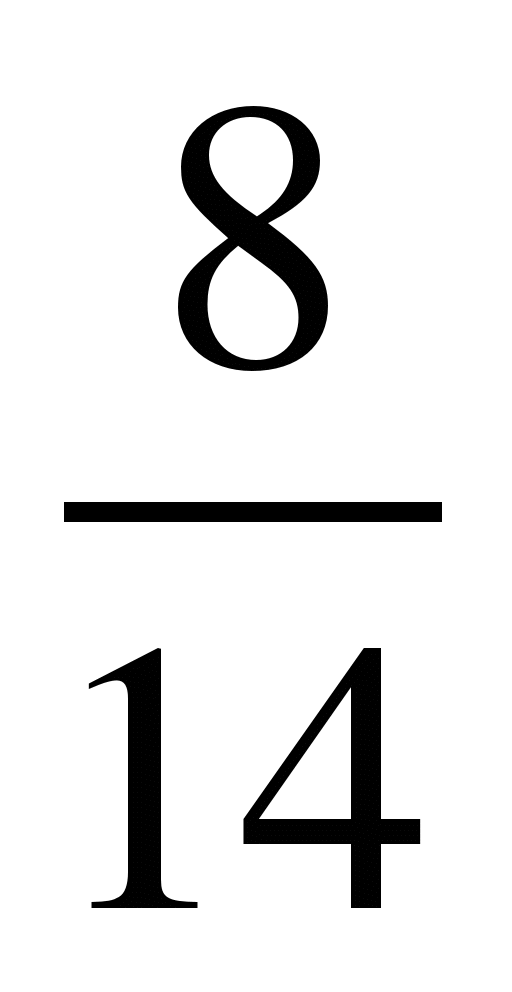 к знаменателю 7.
к знаменателю 7.
Решение.
1) 14 : 2 = 7;
2) 8 : 2 = 4;
3) Ответ: 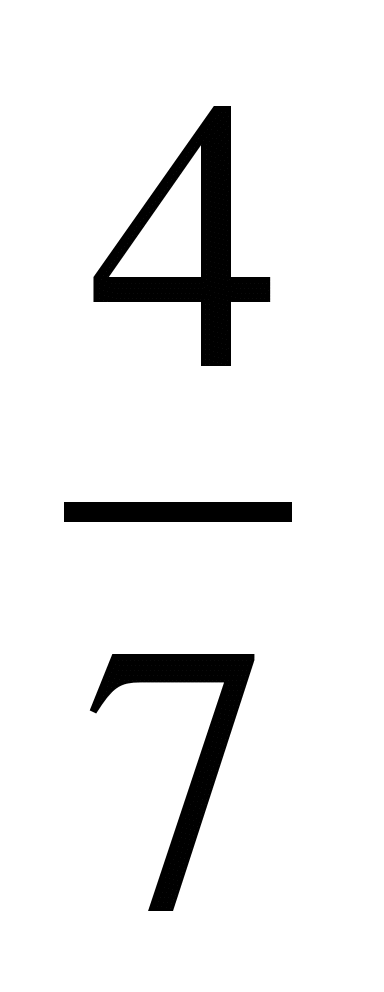 .
.
Привести дроби
к знаменателю 24:
1)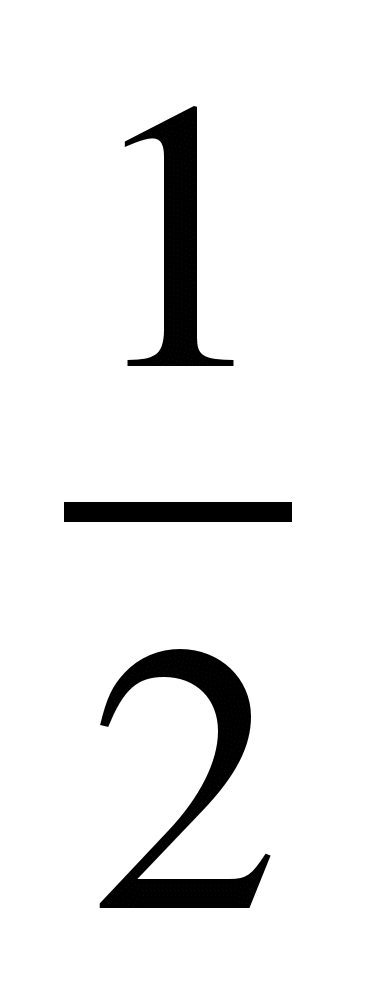 ; 6)
; 6)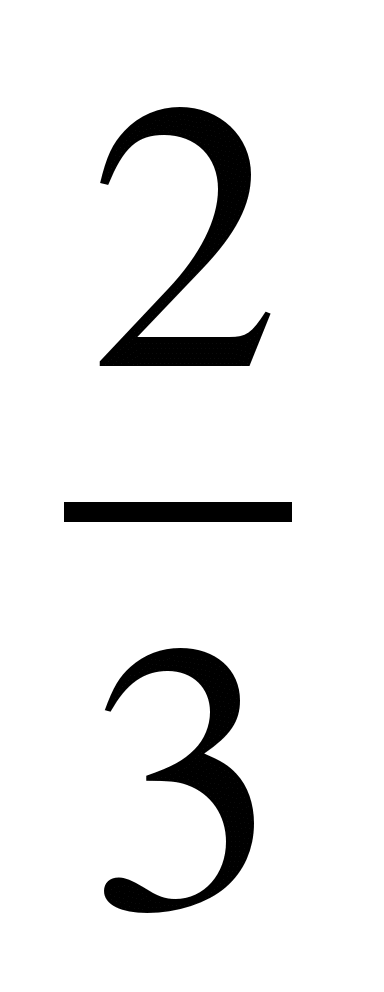 ; 11)
; 11)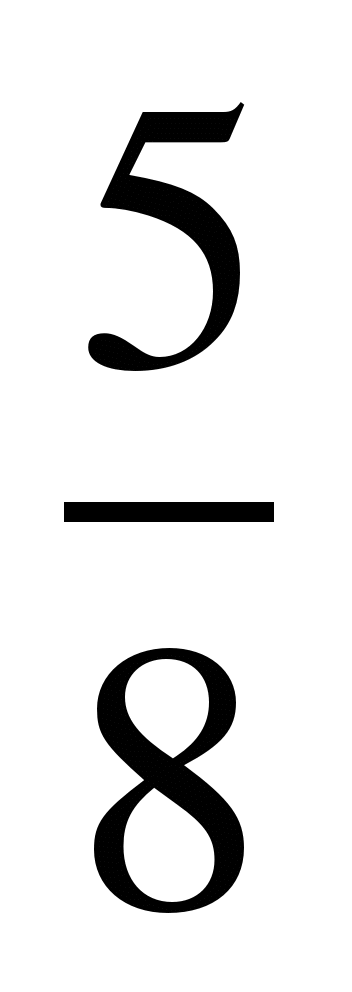 .
.
Привести дроби к знаменателю 7:
2)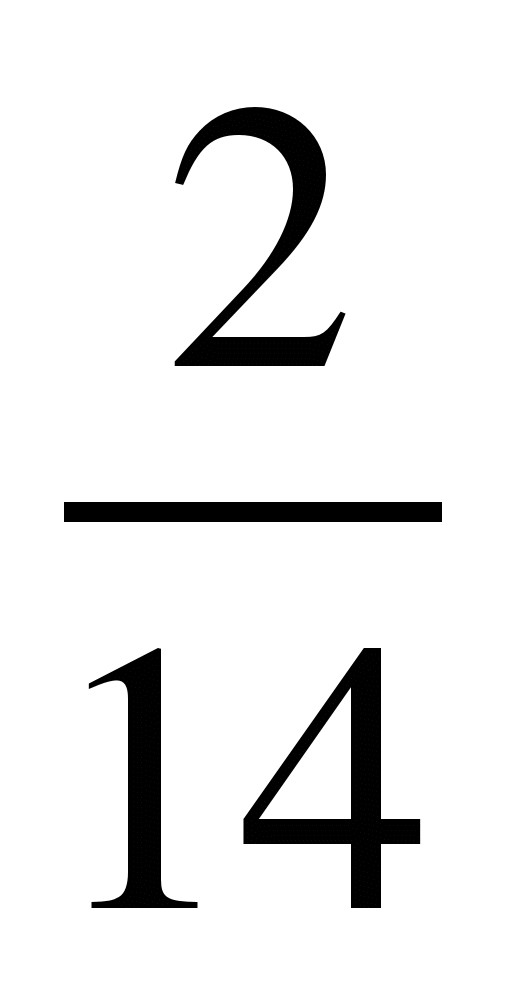 ; 7)
; 7)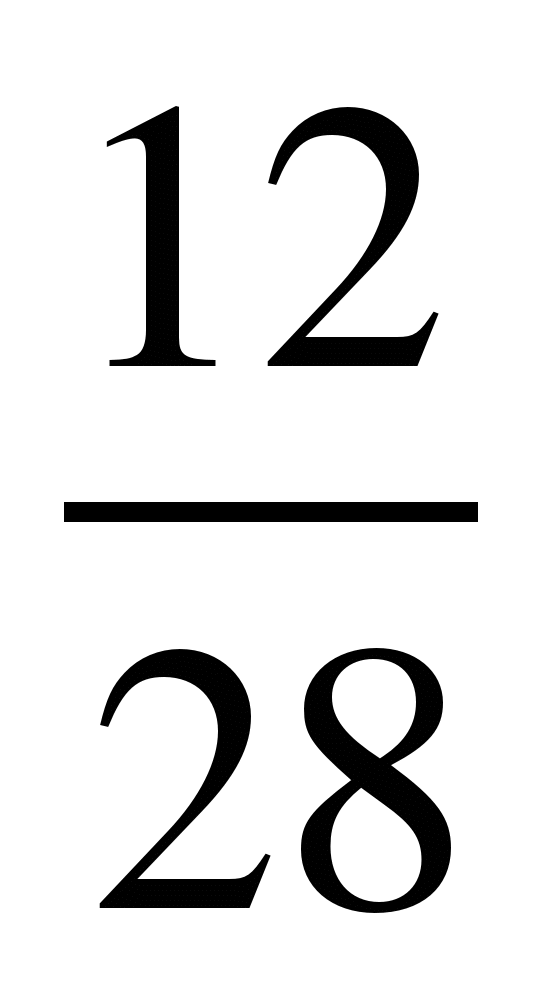 ; 12)
; 12)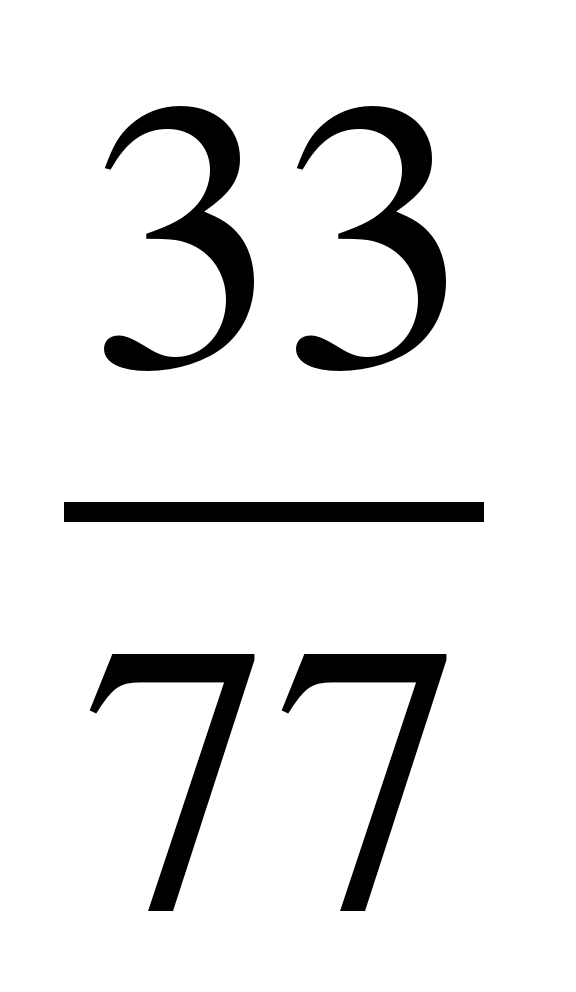 .
.
Разделить числитель и знаменатель дроби на 2:
3)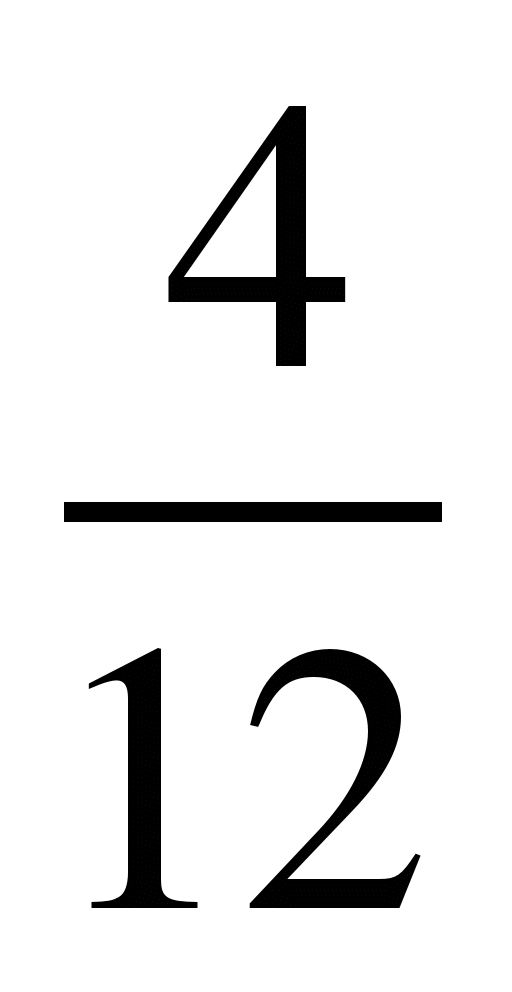 ; 8)
; 8)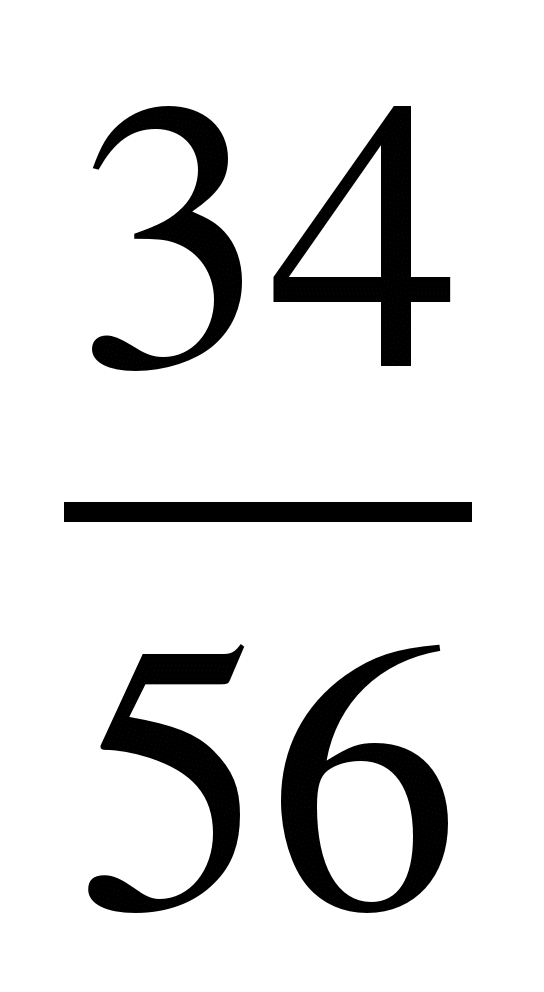 ; 13)
; 13)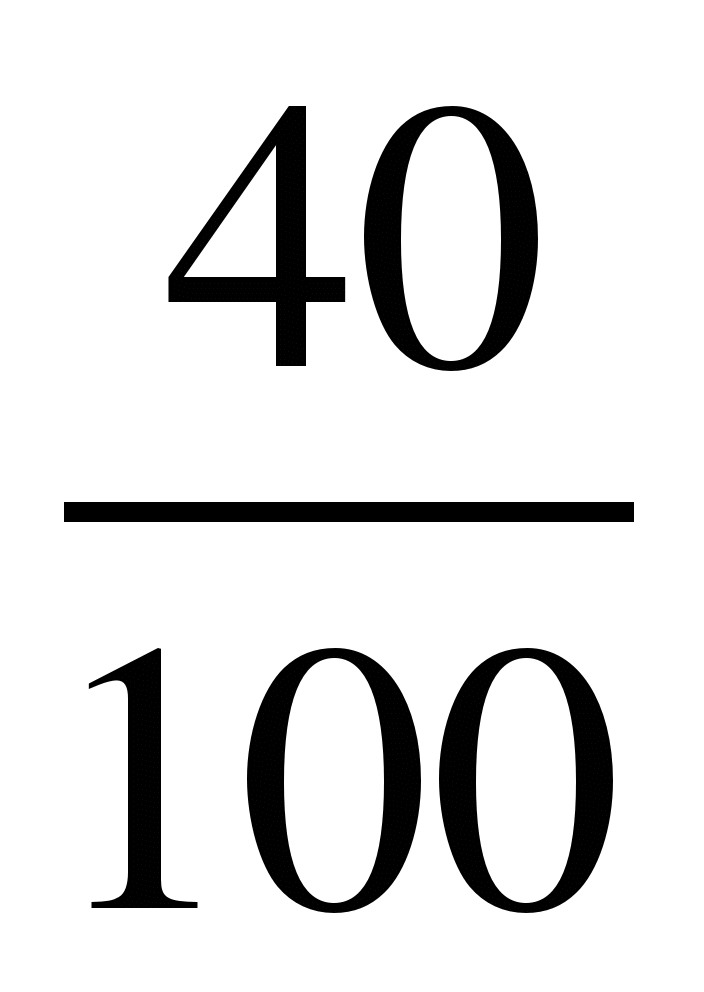 .
.
Умножить числитель и знаменатель дроби на 2:
4)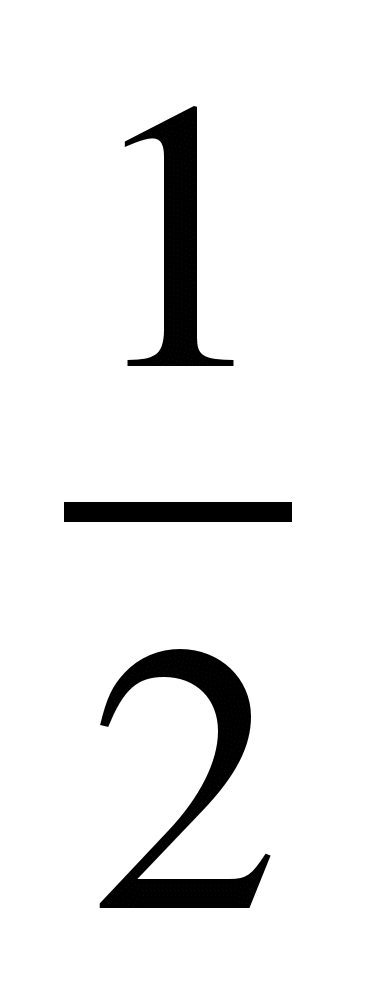 ; 9)
; 9)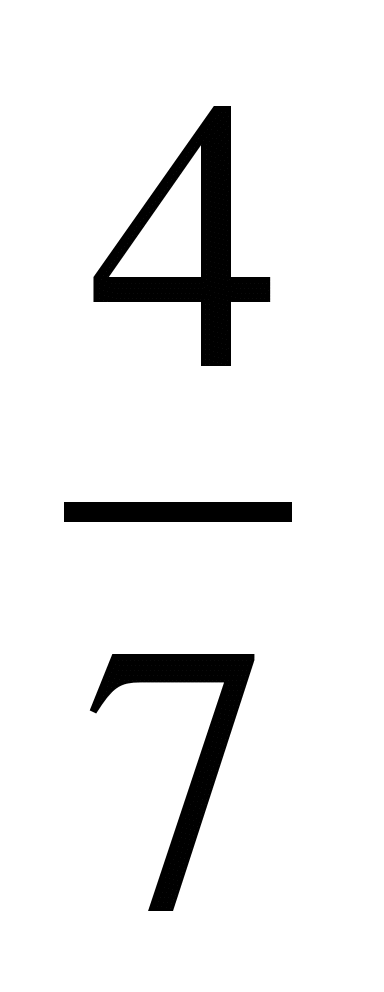 ; 14)
; 14)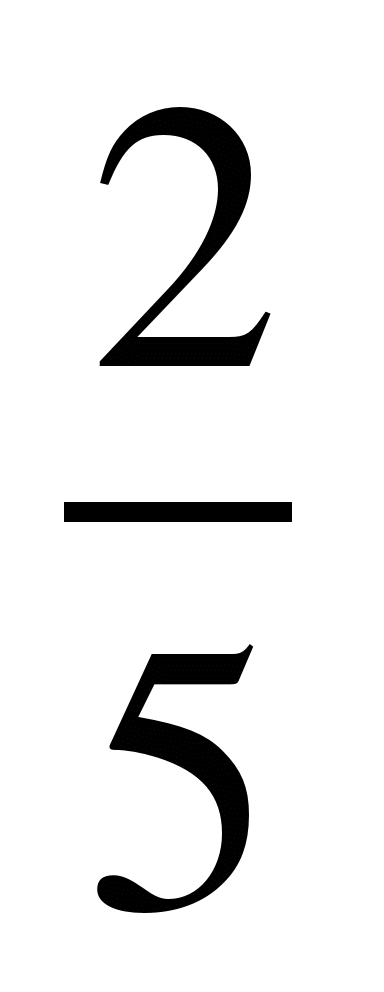 ;
;
Разделить числитель и знаменатель дроби на возможно большее число:
5)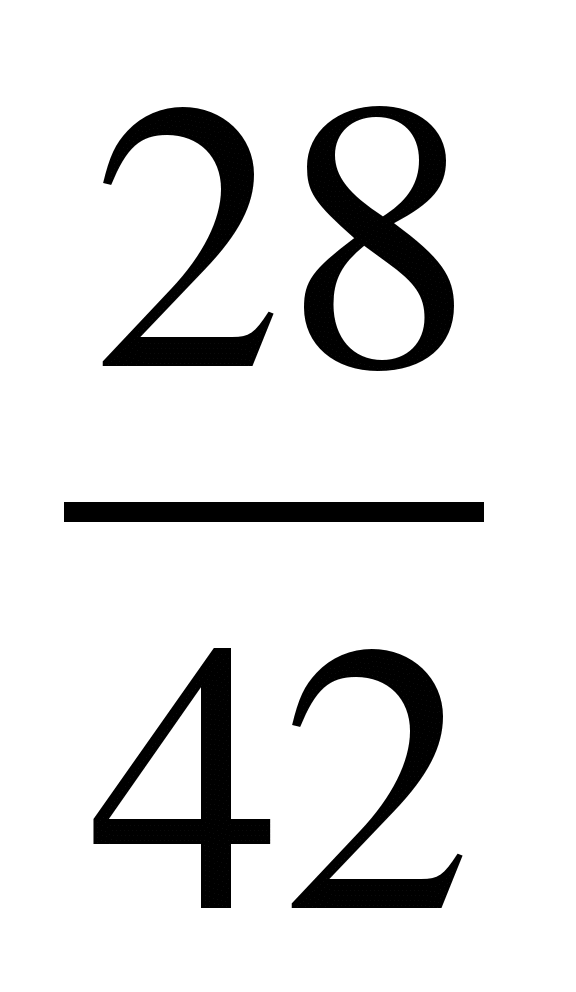 ; 10)
; 10)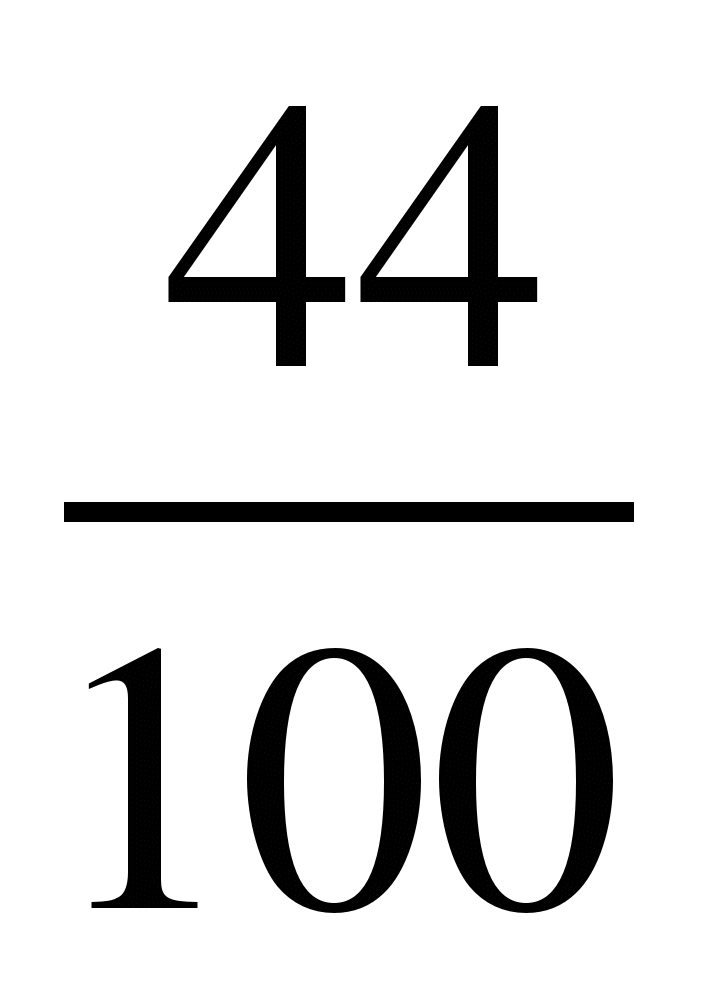 ; 15)
; 15)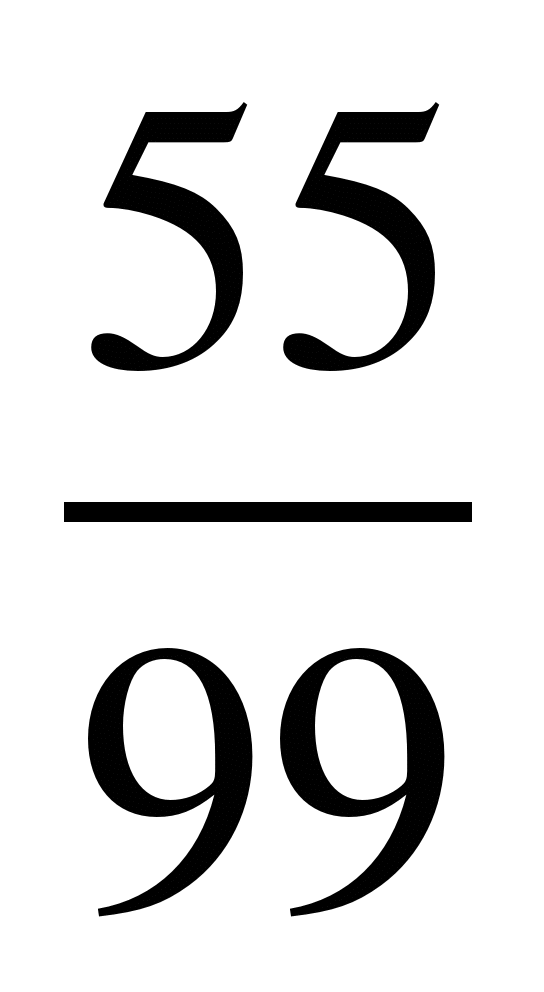 .
.
Сравнение, сложение и вычитание дробей с разными знаменателями.
1) Привести дроби к наименьшему общему знаменателю.
2) Сравнить,
сложить или
вычесть получившиеся дроби
с одинаковыми знаменателями.
Сравнить 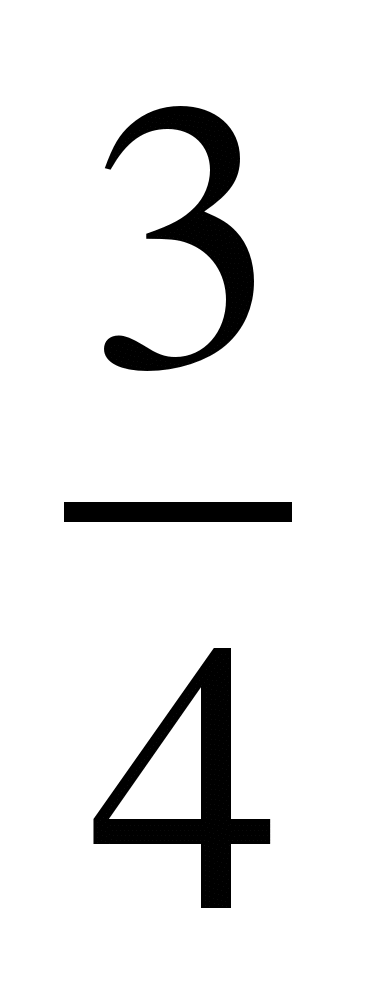 и
и 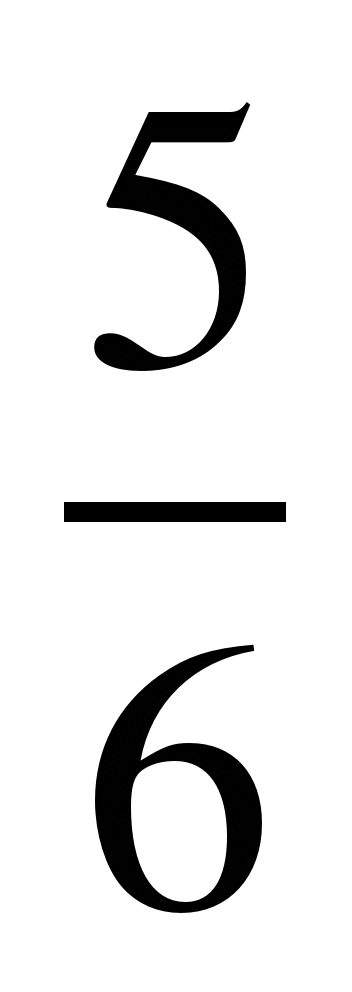 , найти их сумму и разность.
, найти их сумму и разность.
Решение.
1) 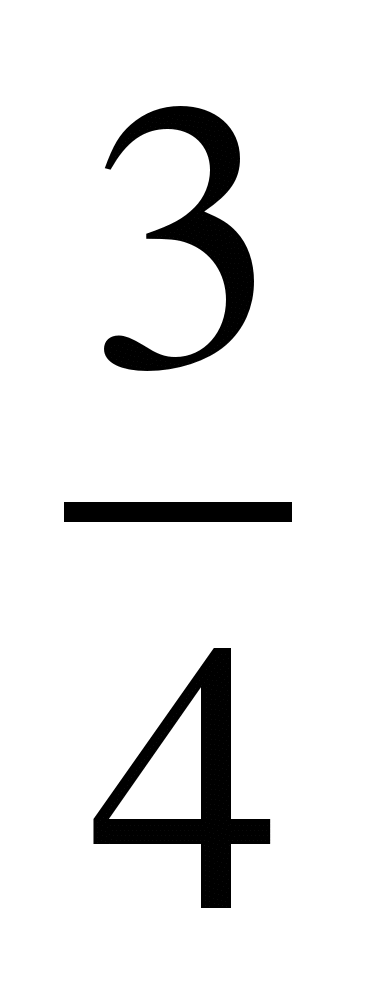 =
= 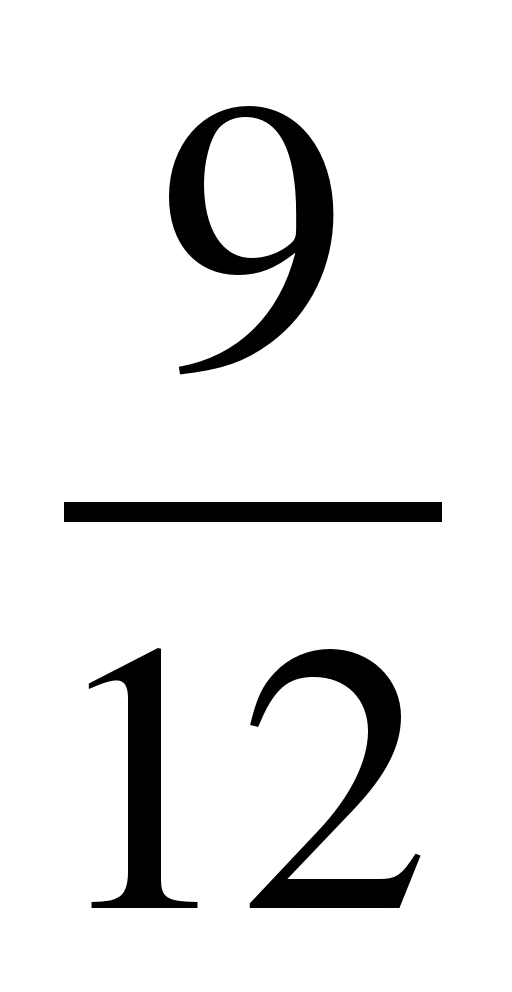 ,
, 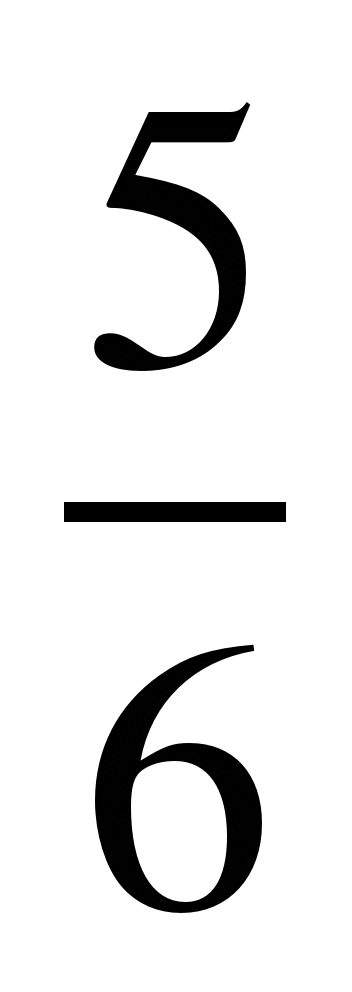 =
= 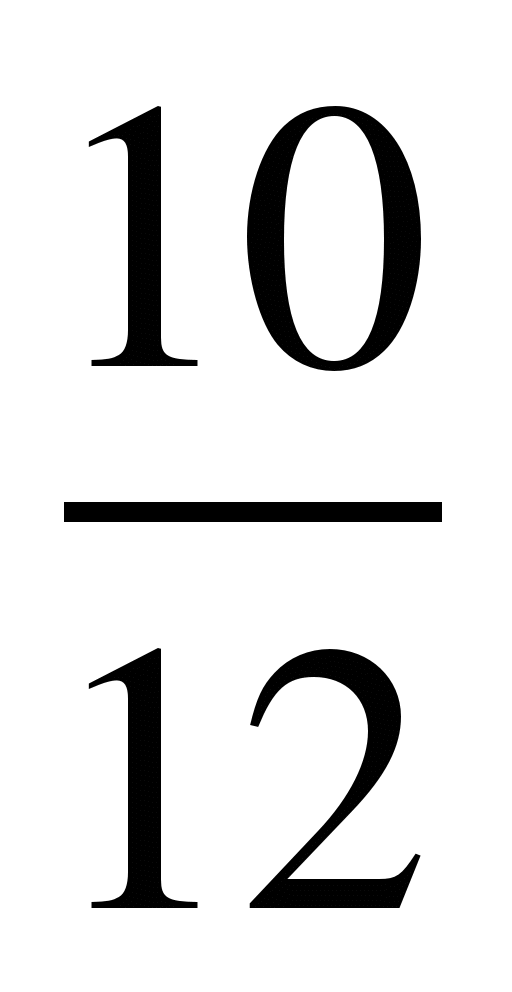 ;
;
2) 9 < 10, значит, 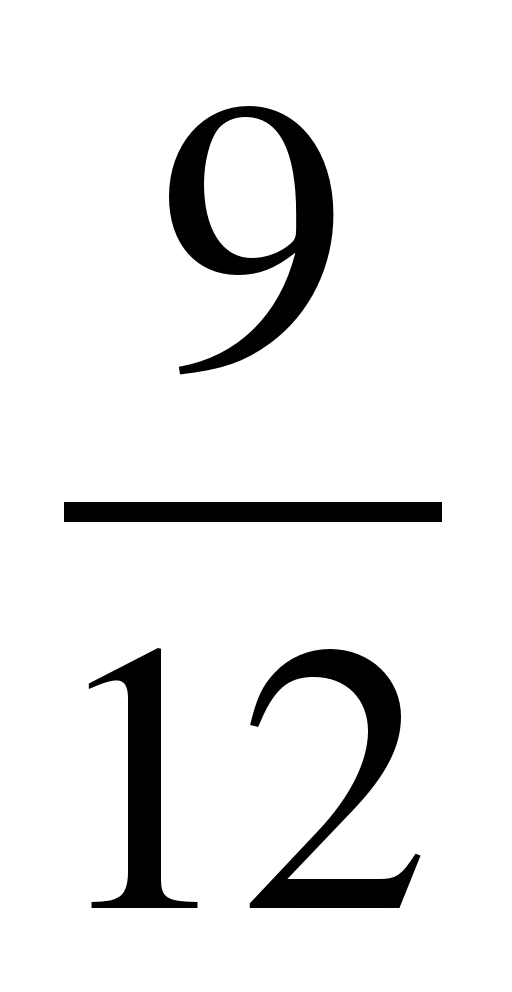 <
< 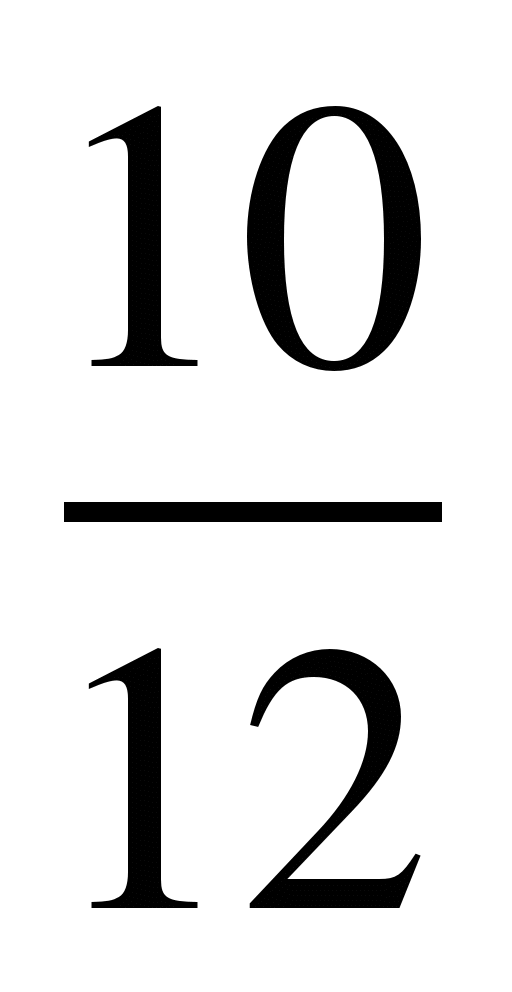 , то есть
, то есть
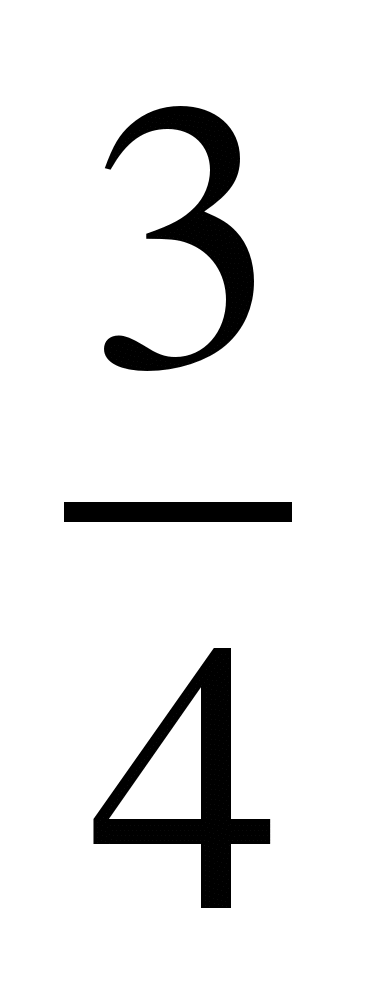 <
< 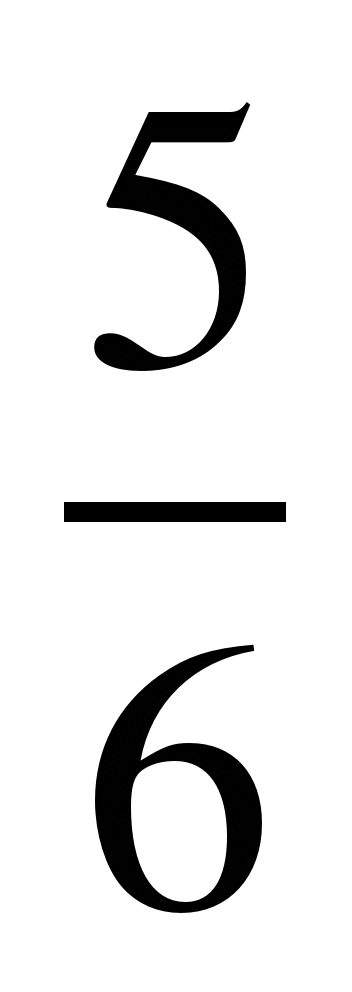 ;
;
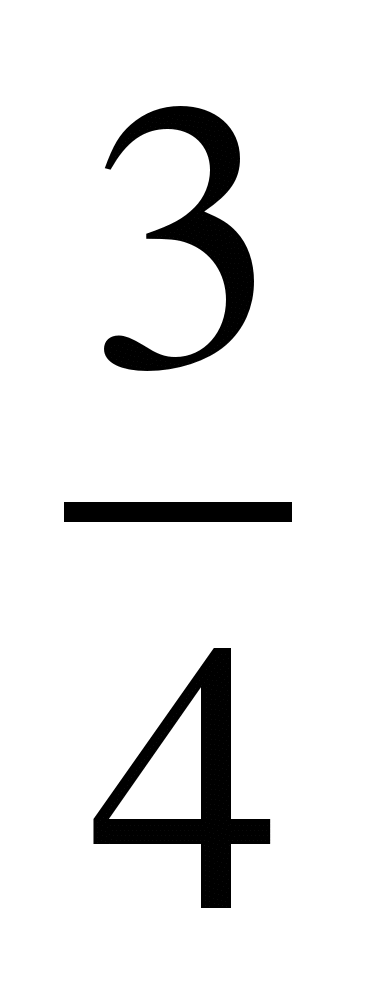 +
+ 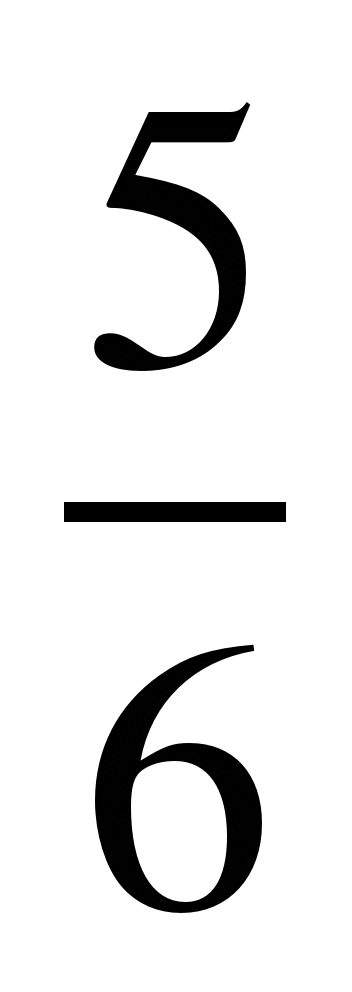 =
= 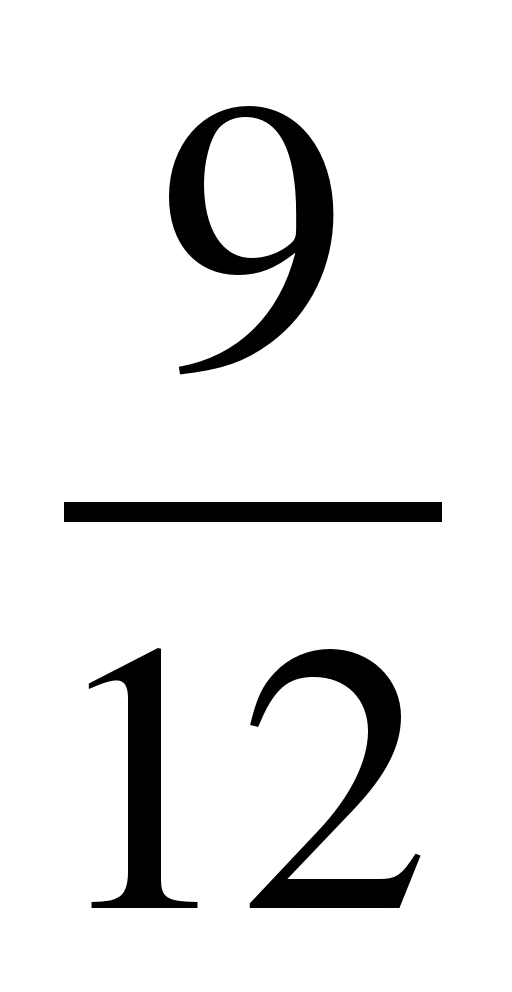 +
+ 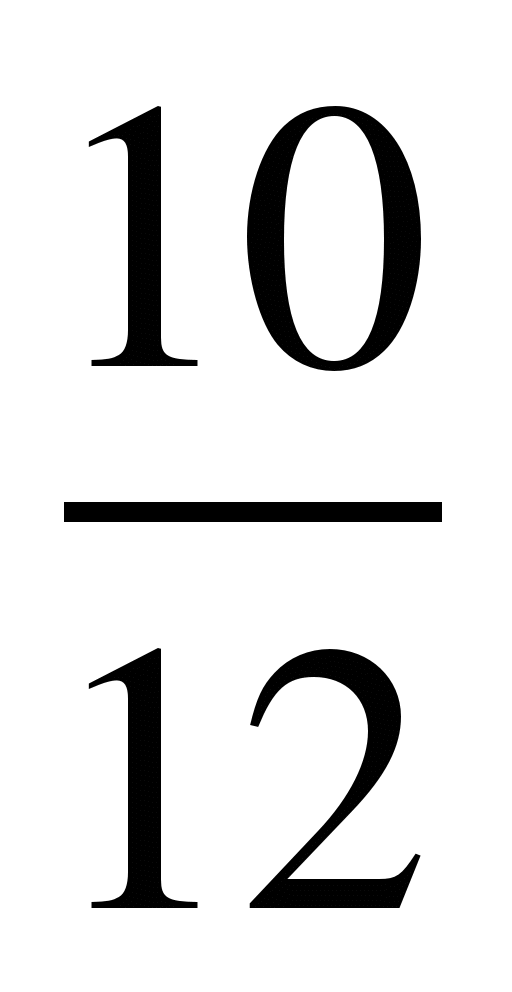 =
=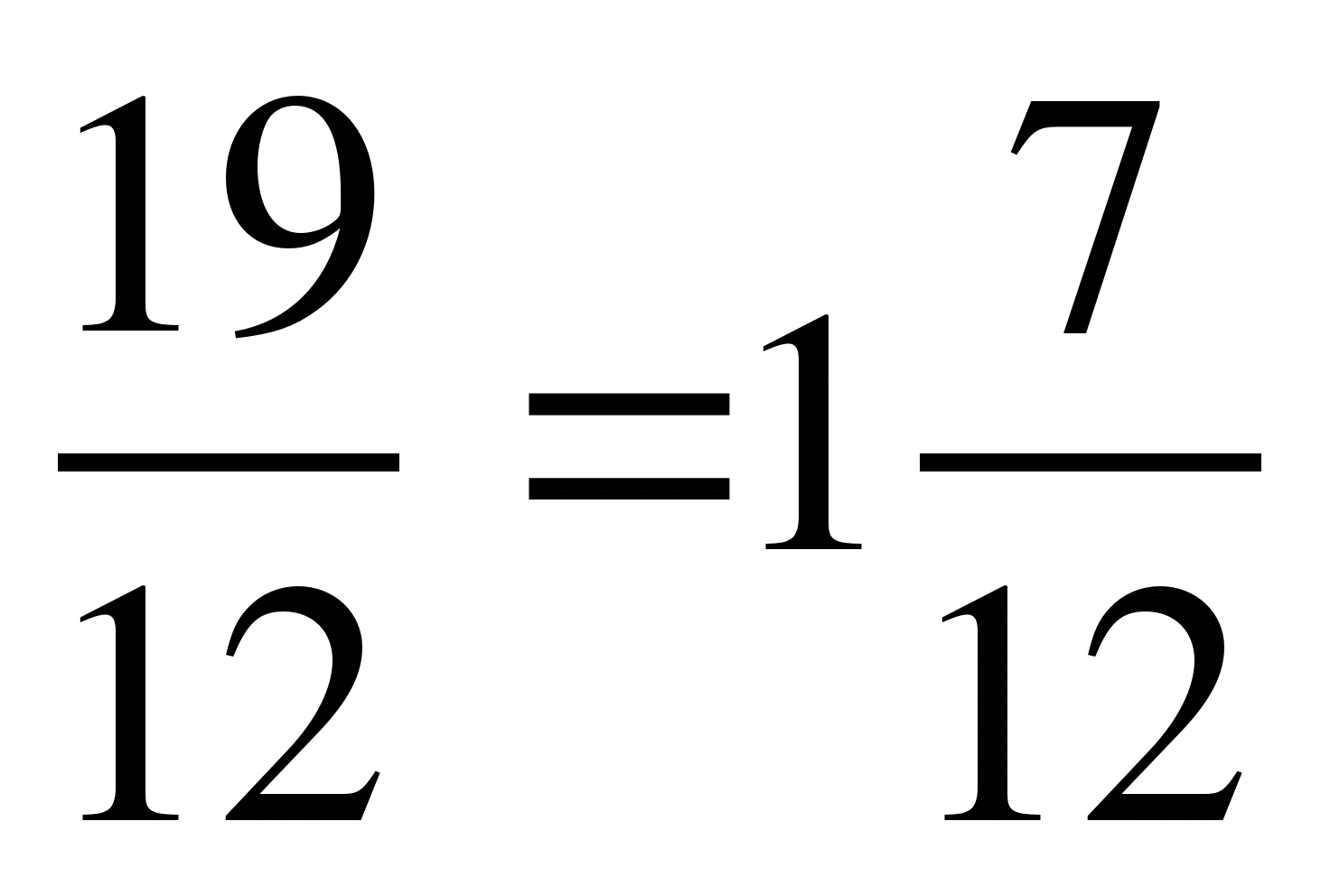 .
.
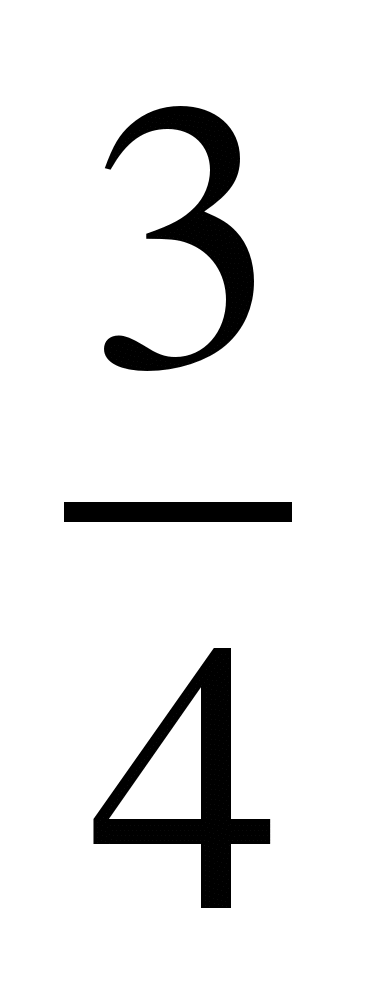 –
– 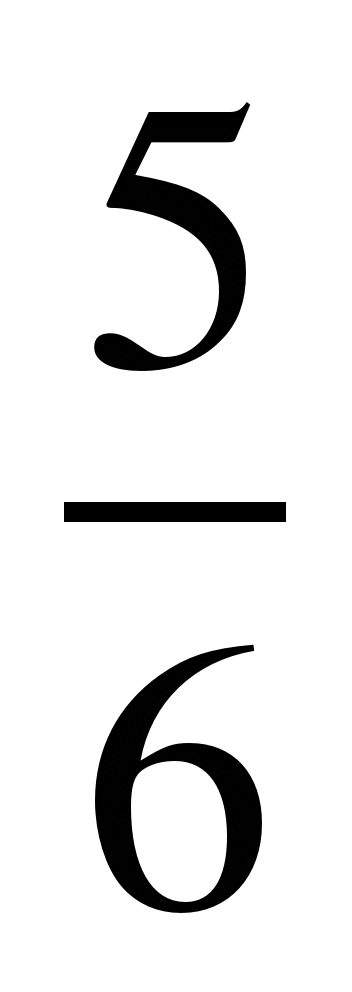 =
= 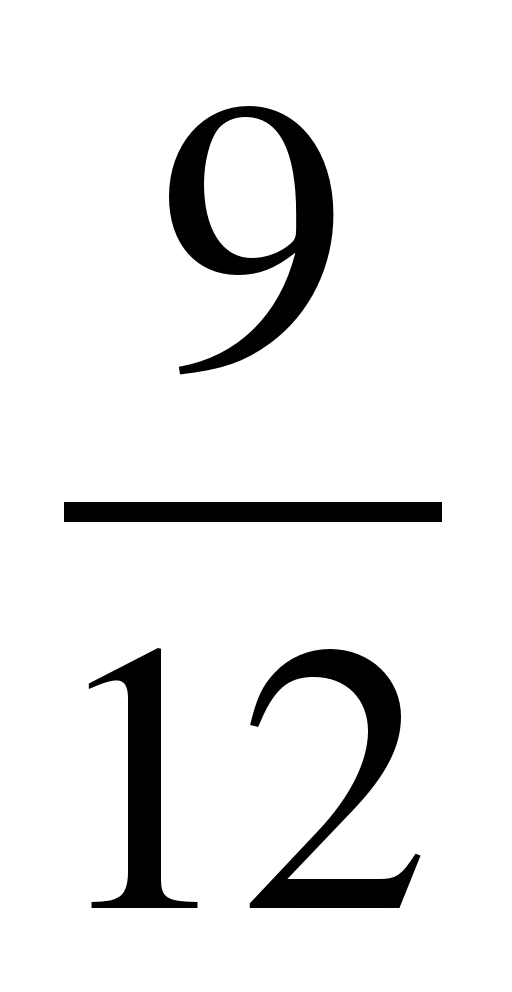 –
– 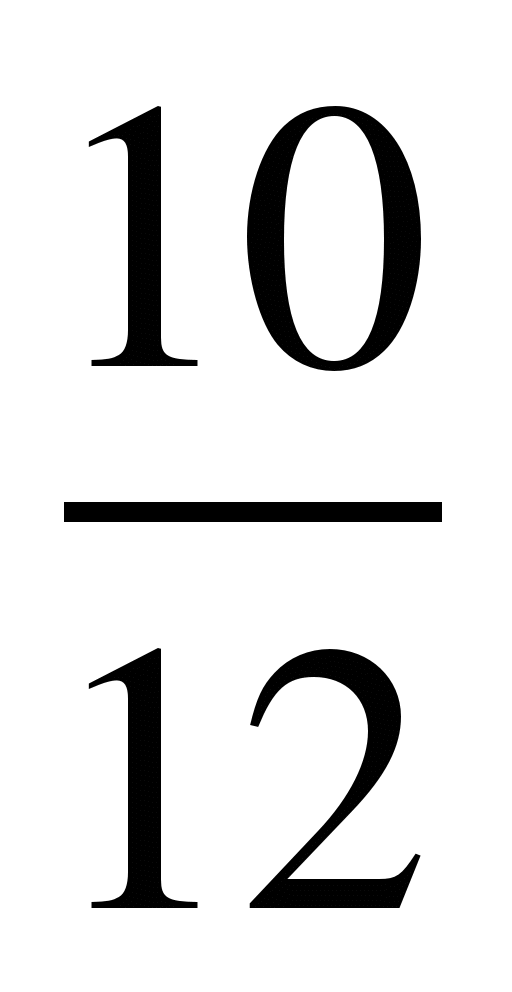 =
= 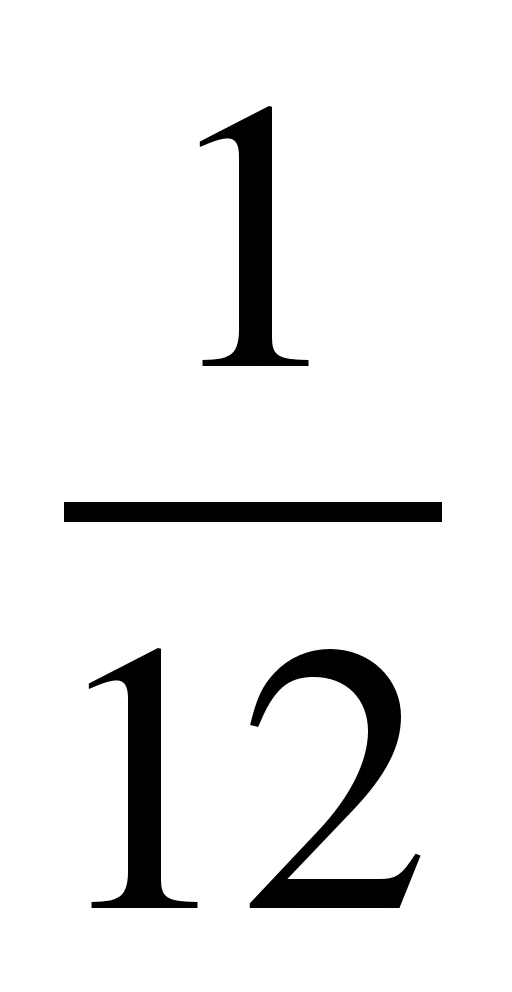 .
.
Сравнить дроби, найти их сумму и разность:
1) 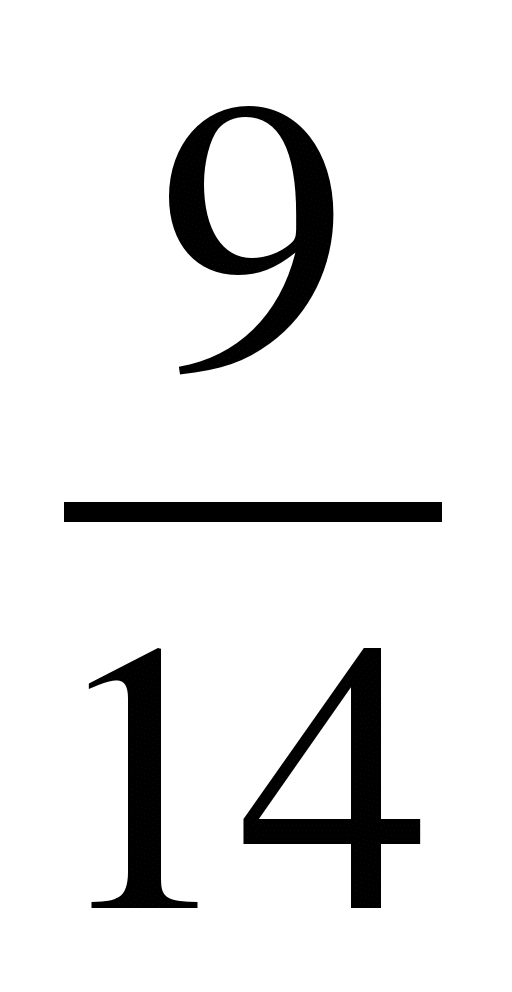 и
и 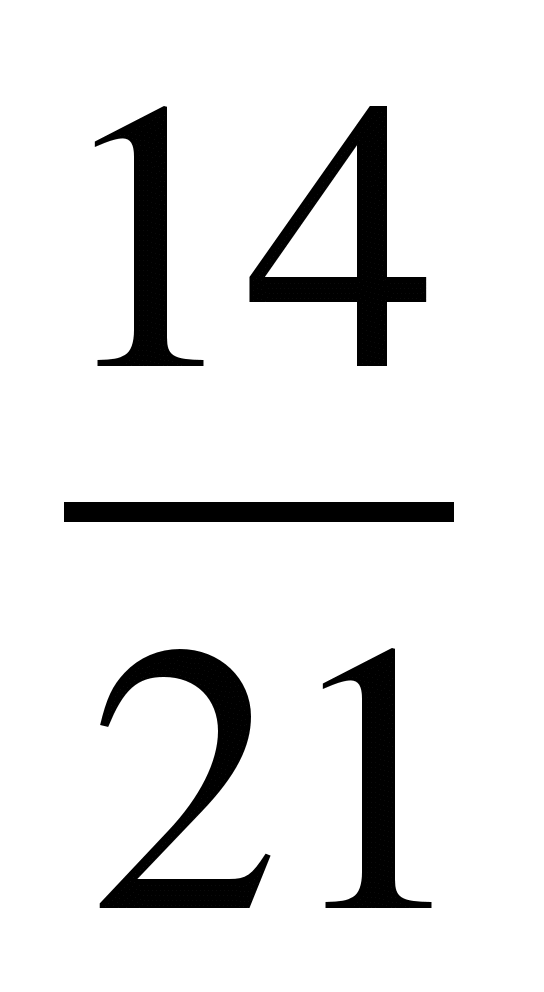 ; 9)
; 9) 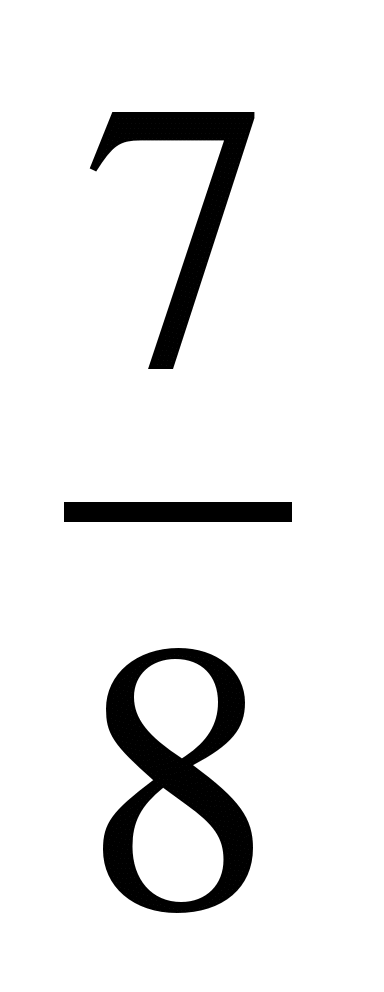 и
и 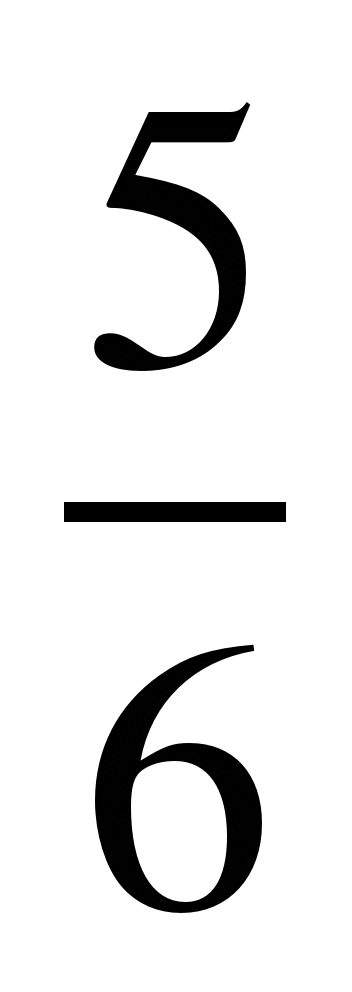 ;
;
2)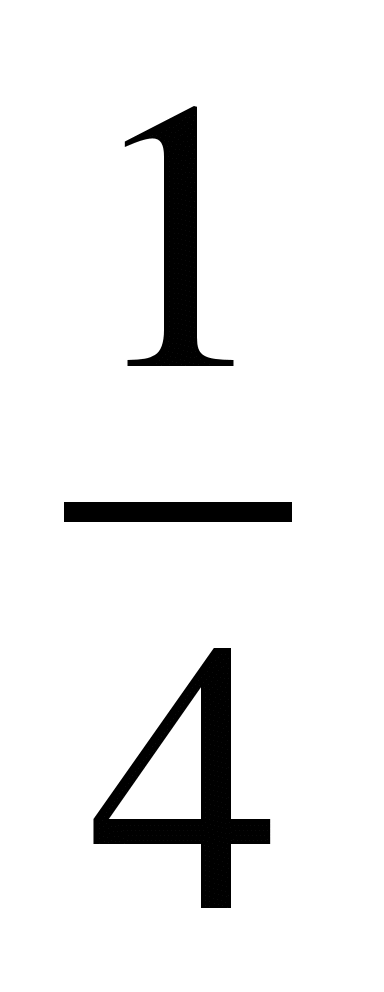 и
и 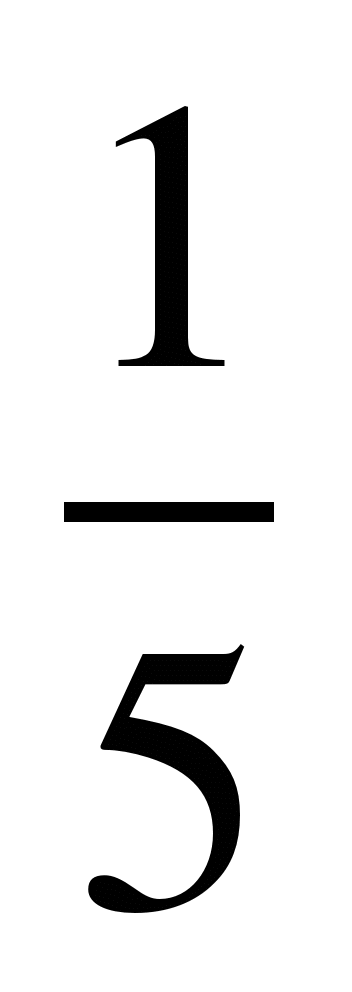 ; 10)
; 10) 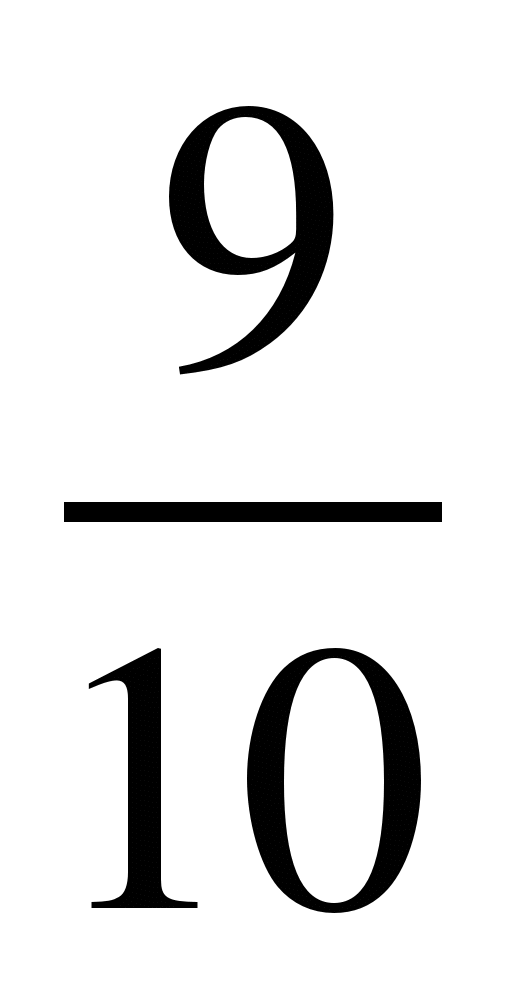 и
и 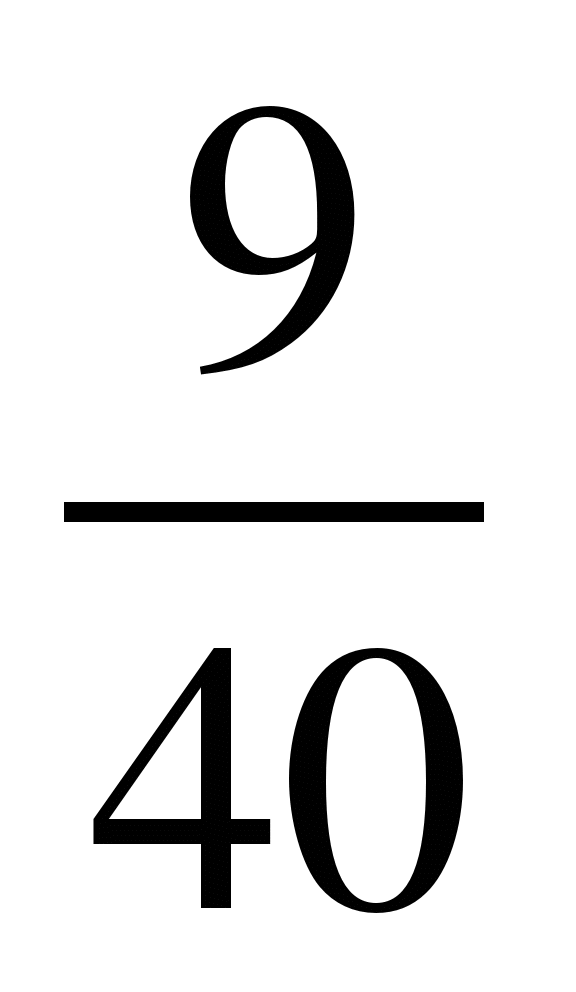 ;
;
3) 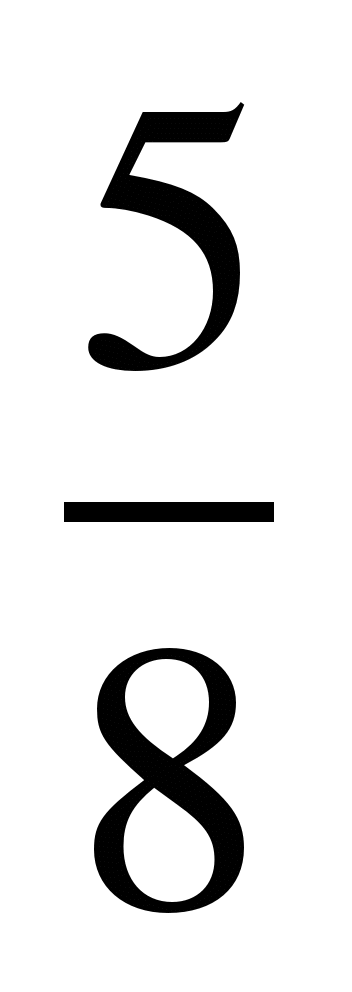 и
и 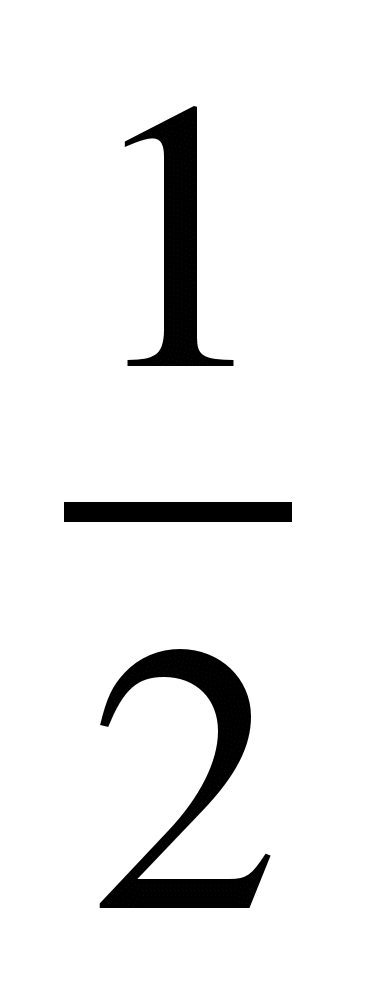 ; 11)
; 11) 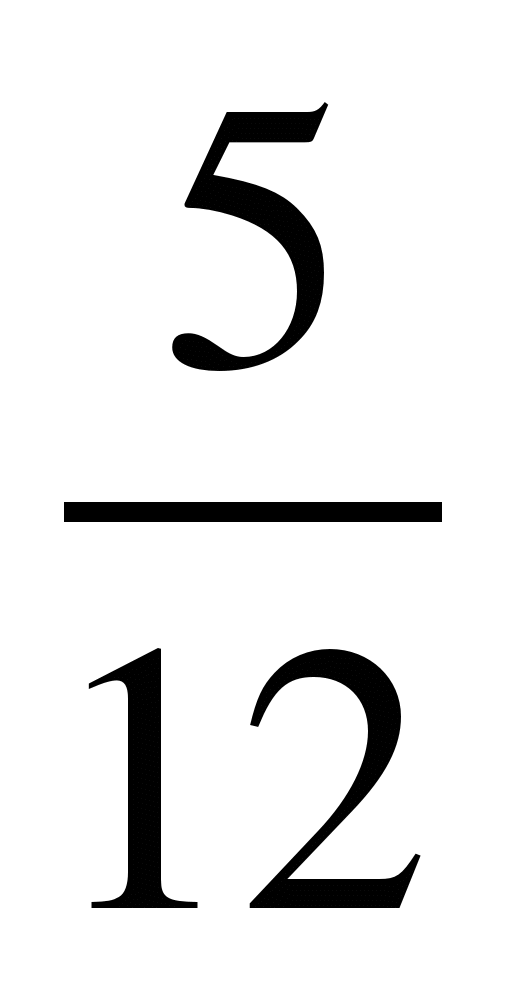 и
и 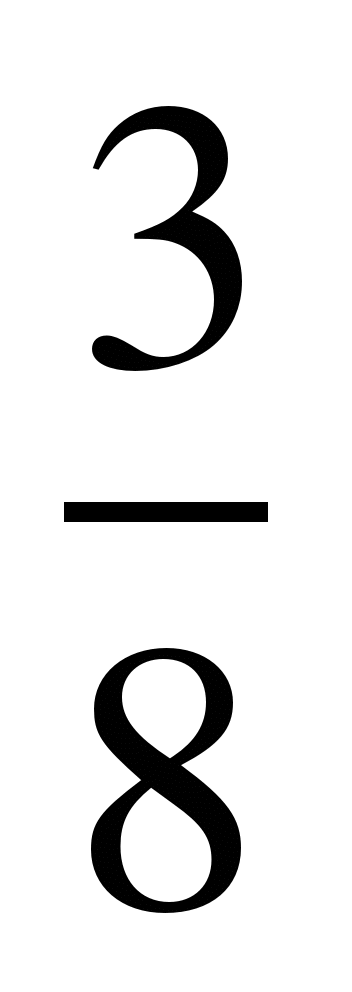 ;
;
4) 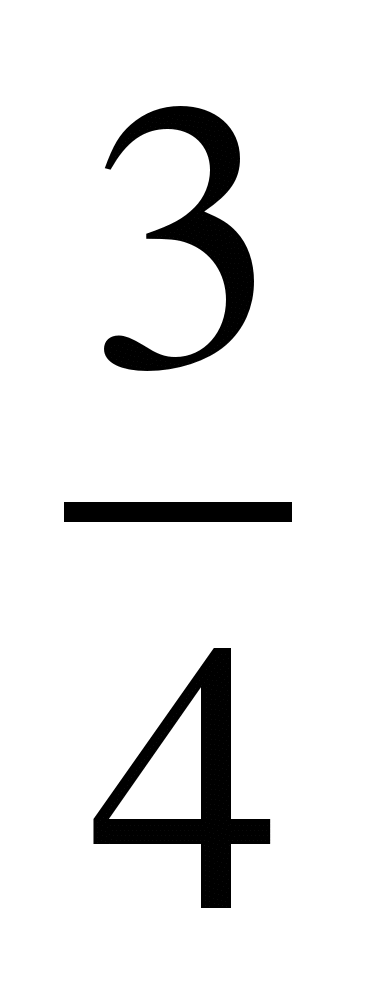 и
и 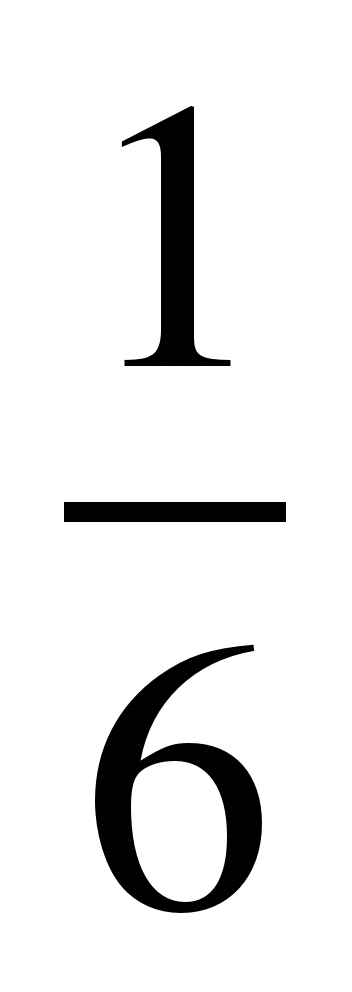 ; 12)
; 12) 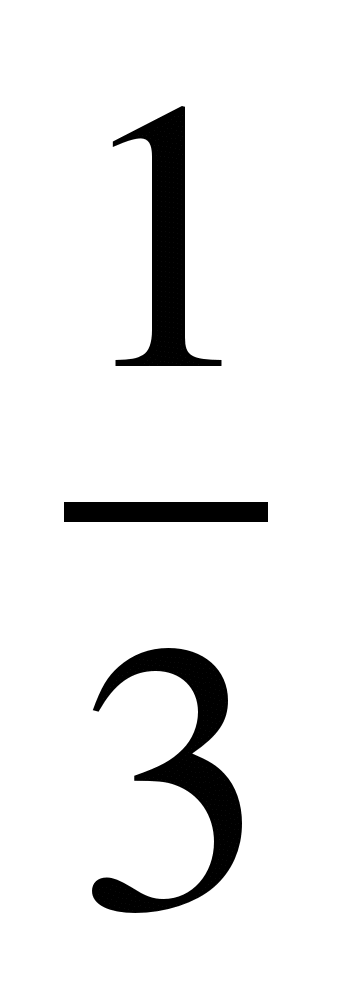 и
и 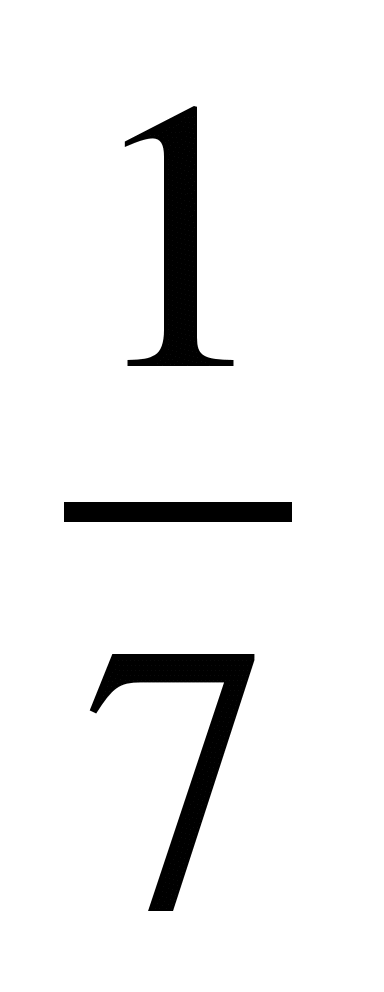 ;
;
5) 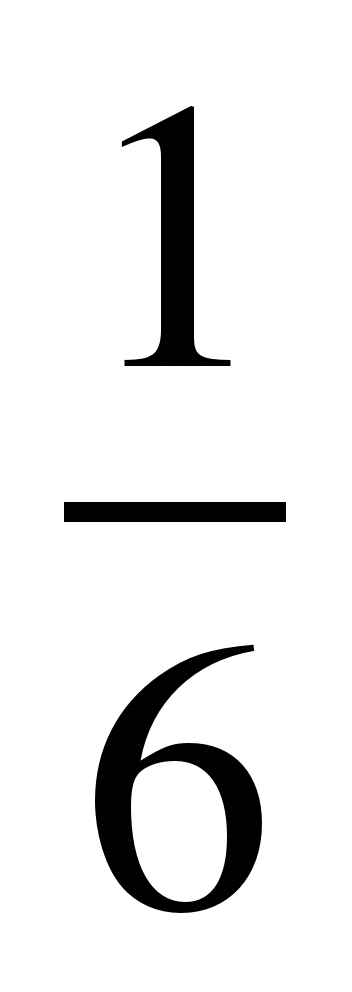 и
и 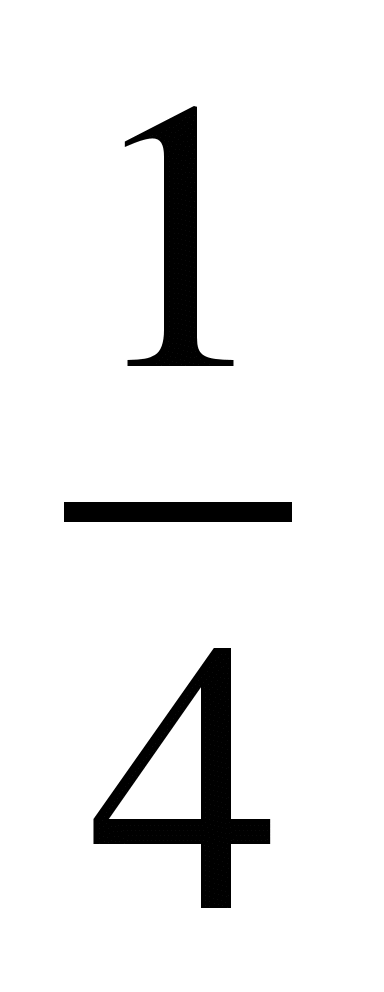 ; 13)
; 13) 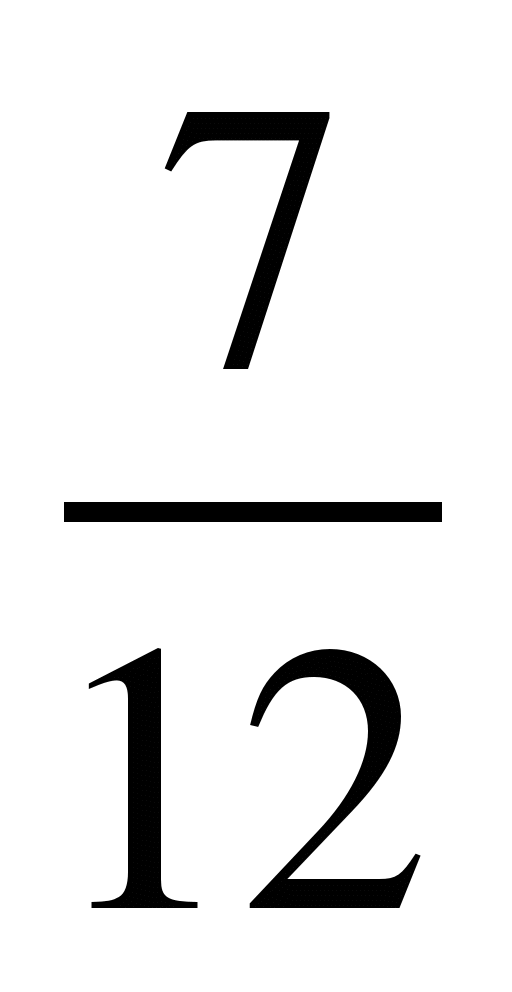 и
и 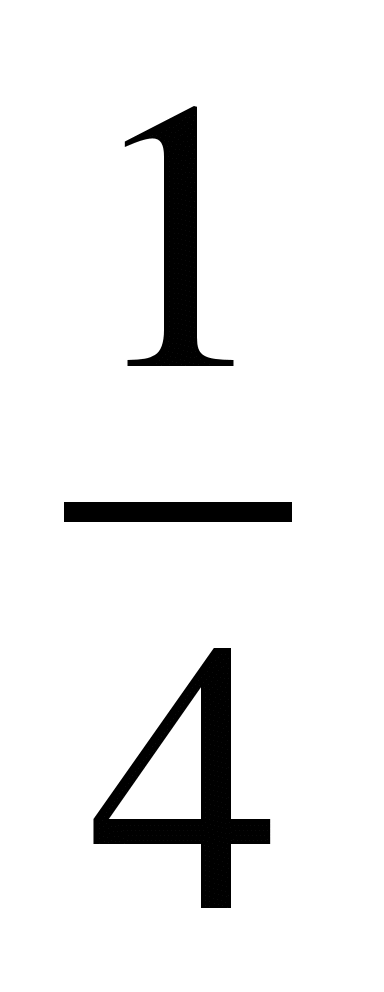 ;
;
6) 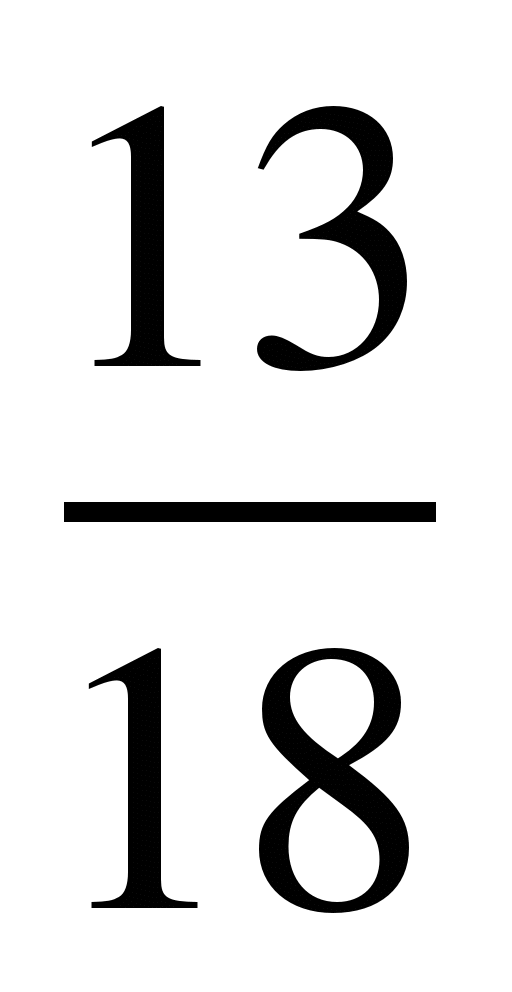 и
и 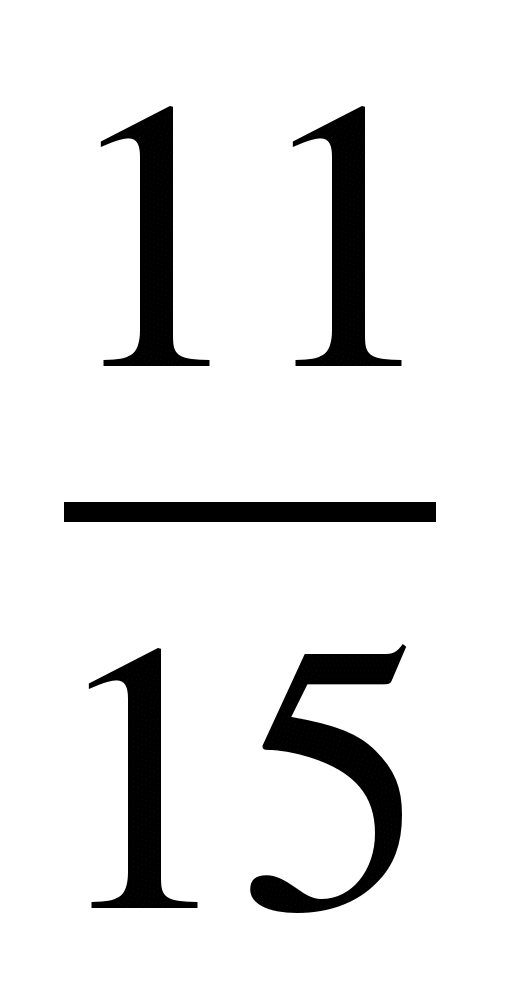 ; 14)
; 14) 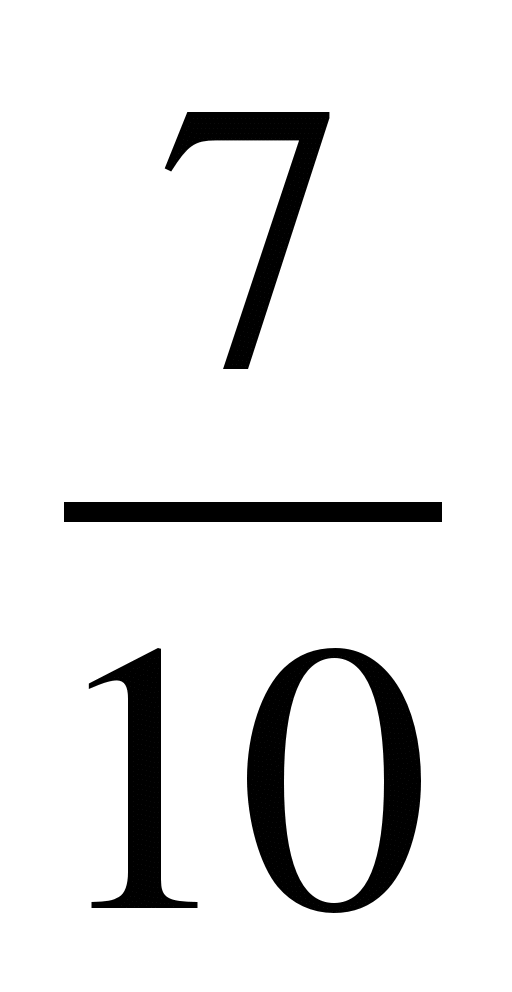 и
и 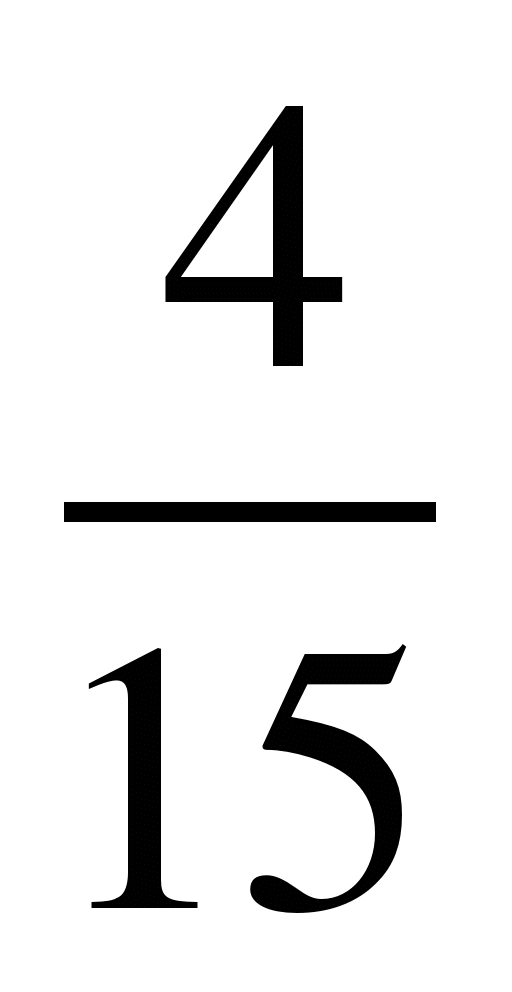 ;
;
Умножение дробей.
Умножь числитель на числитель и знаменатель на знаменатель:
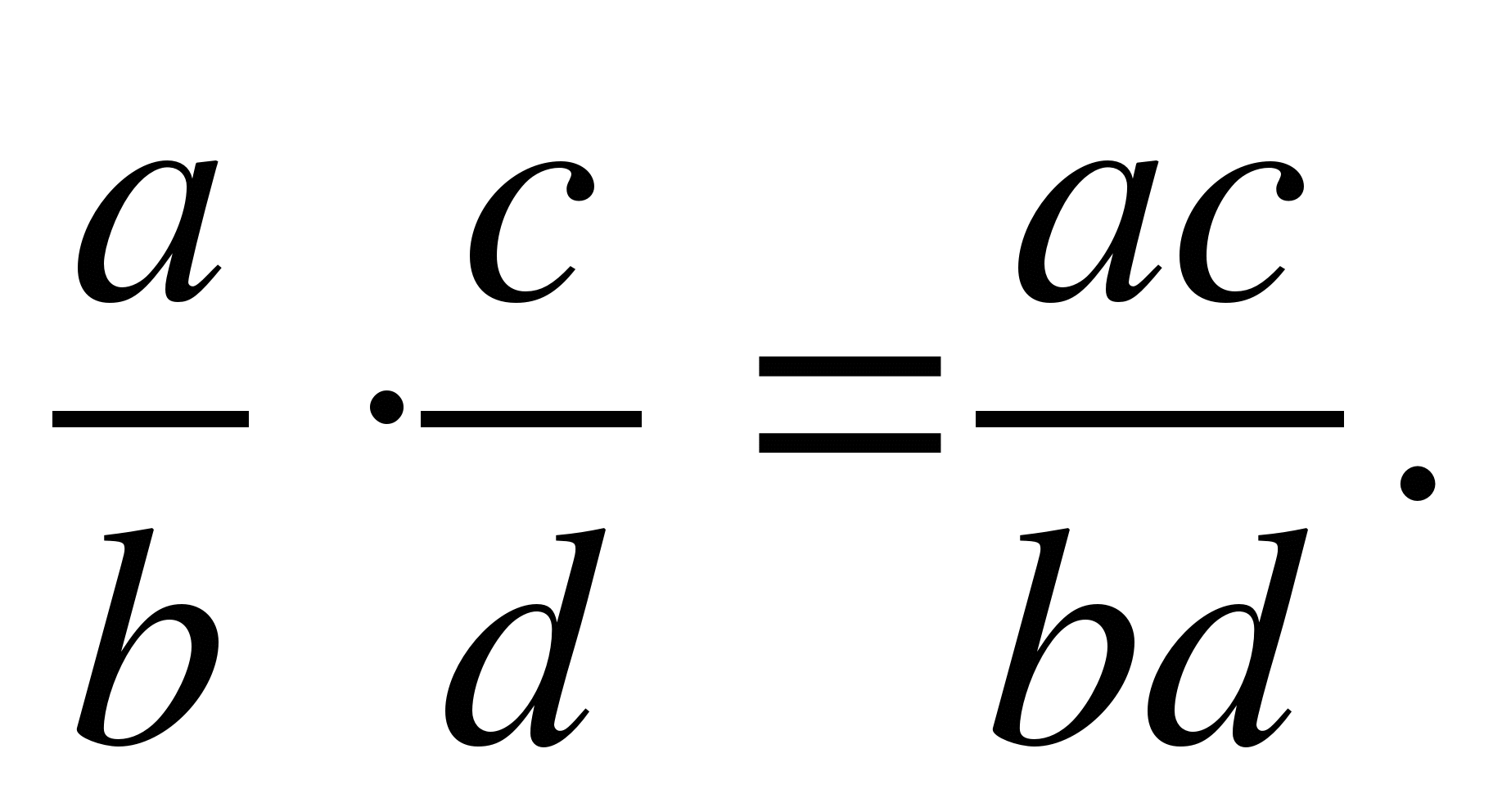
1)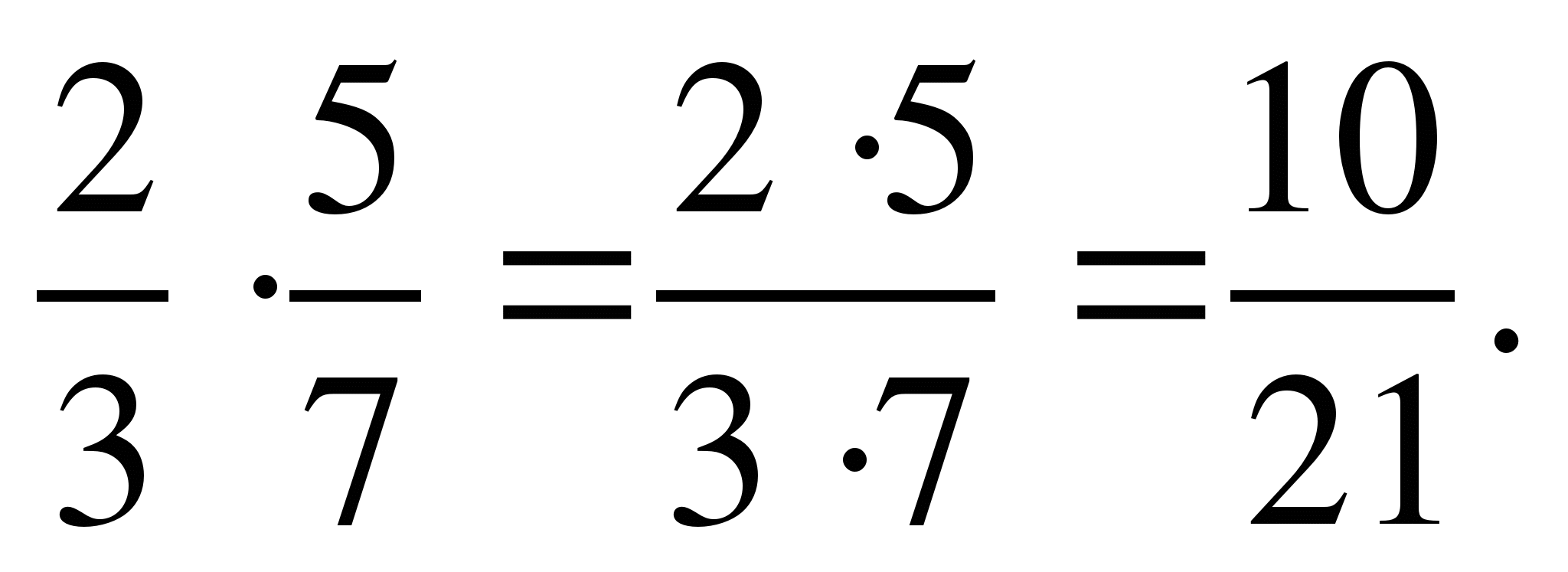
2) 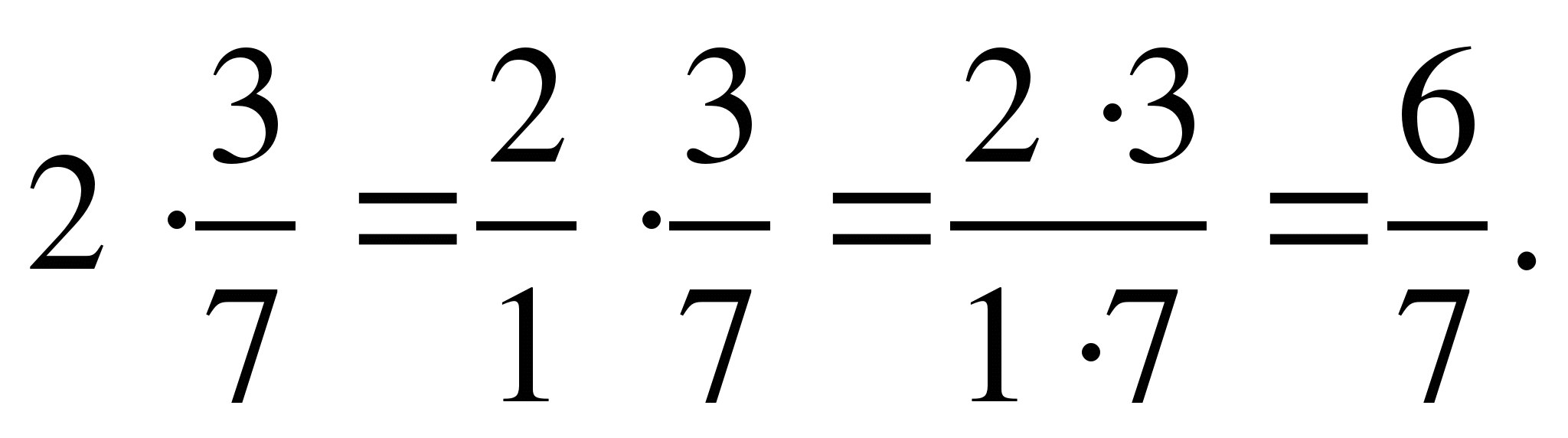
3) 
= 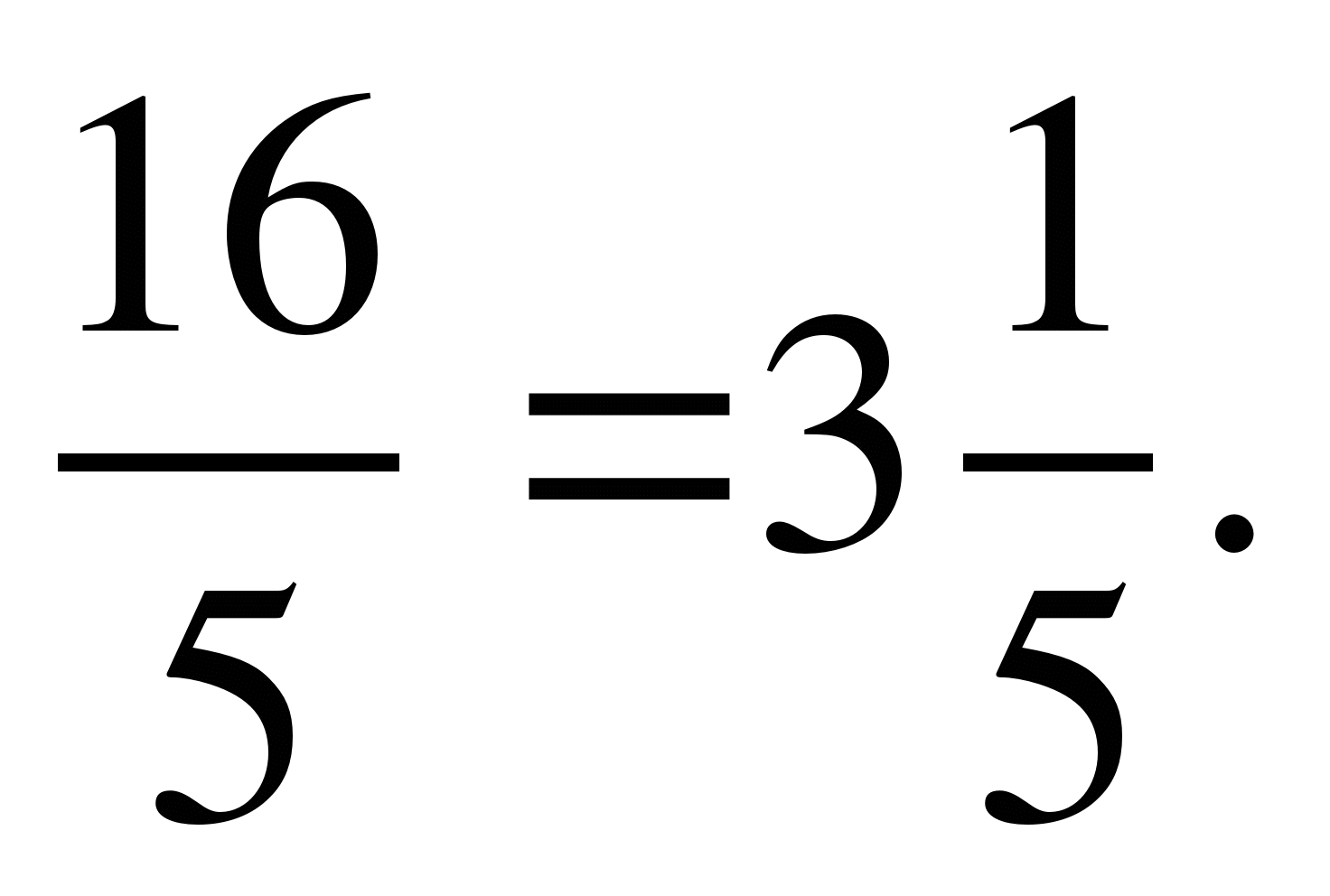
Найдите произведение дробей:
1)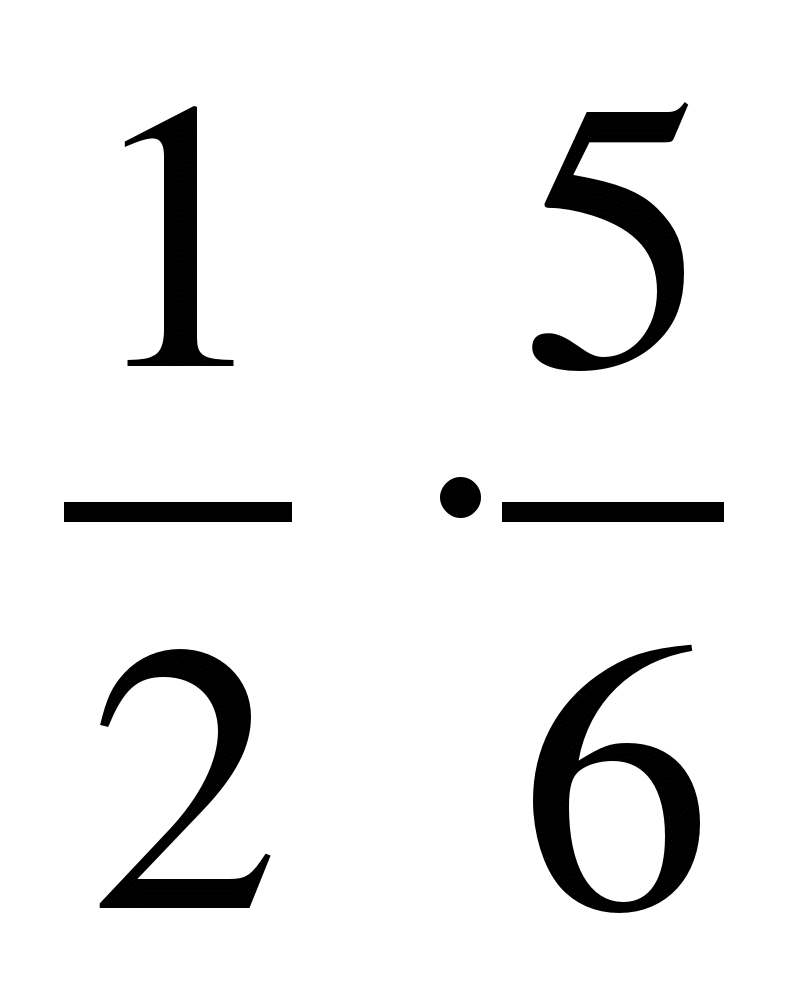 ; 2)
; 2) 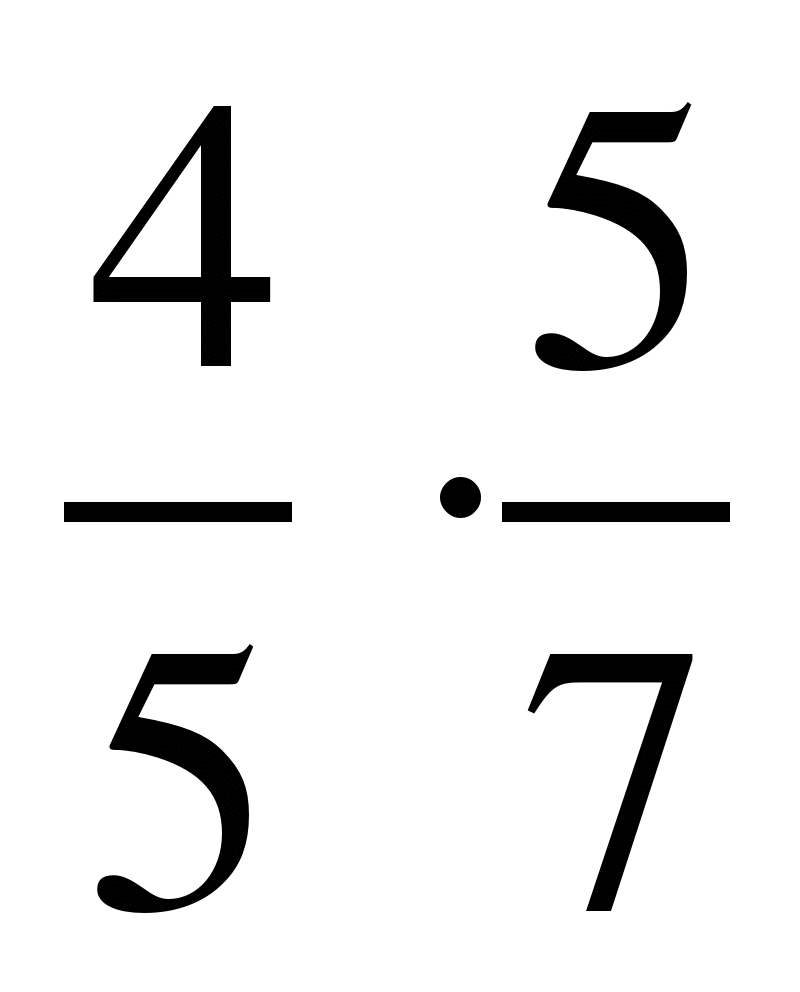 ;
;
3) 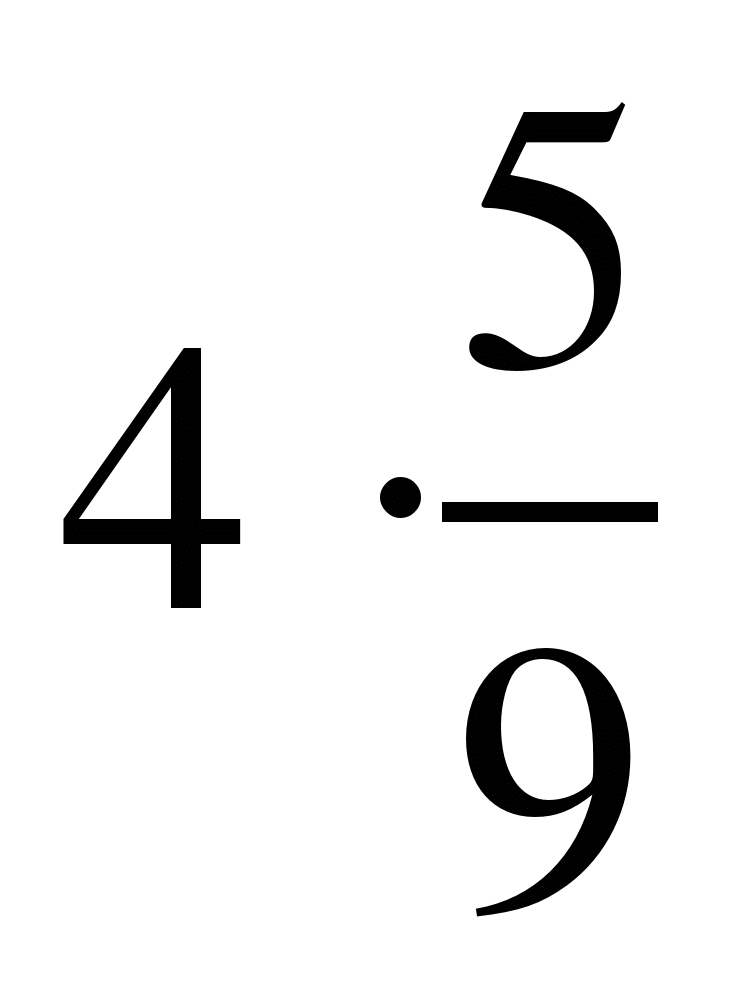 ; 4)
; 4) 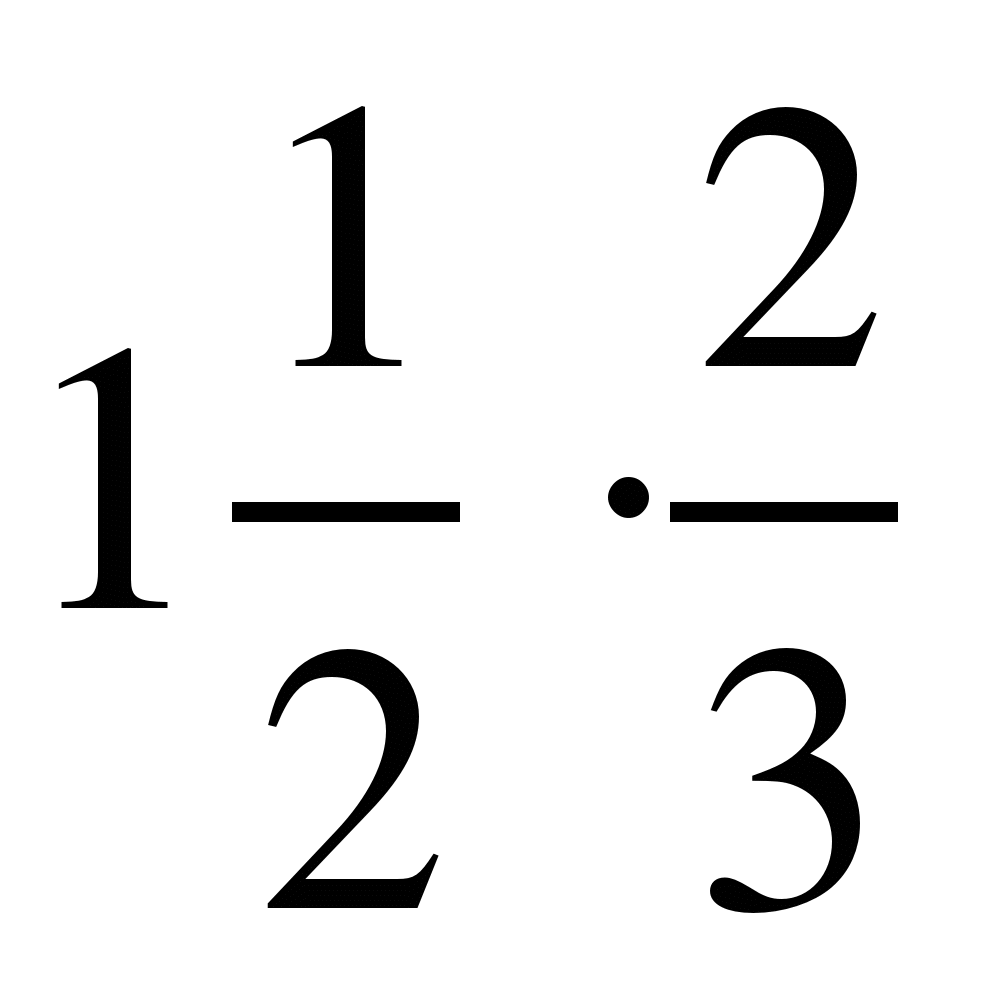 ;
;
5) 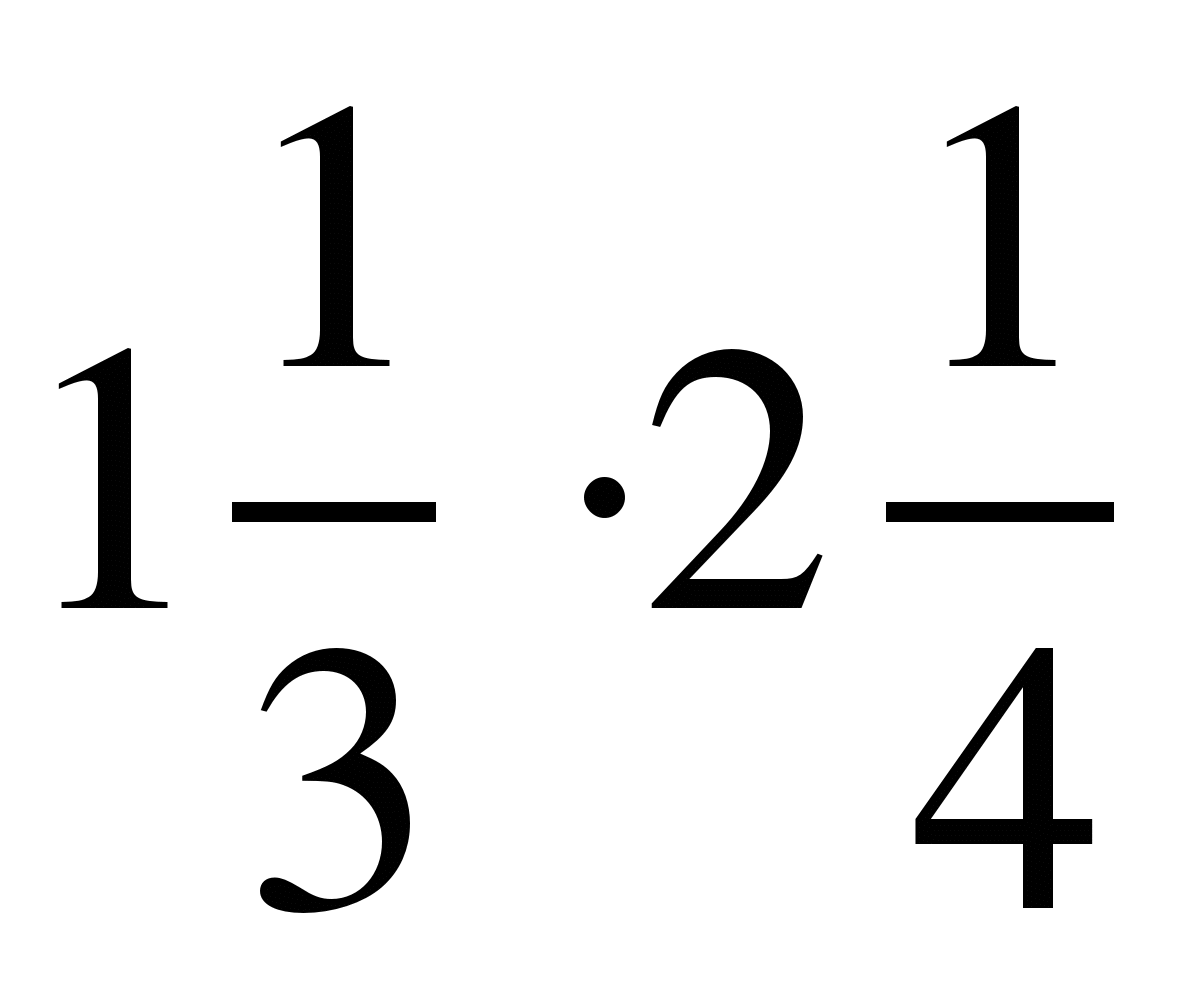 ; 6)
; 6) 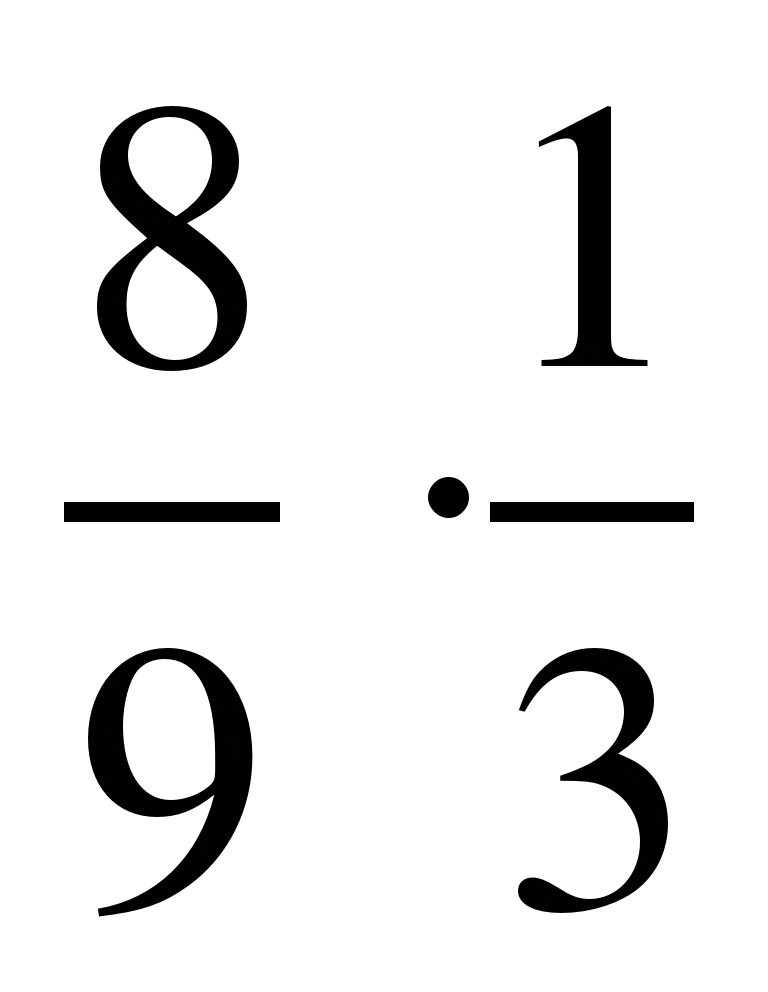 ;
;
7) 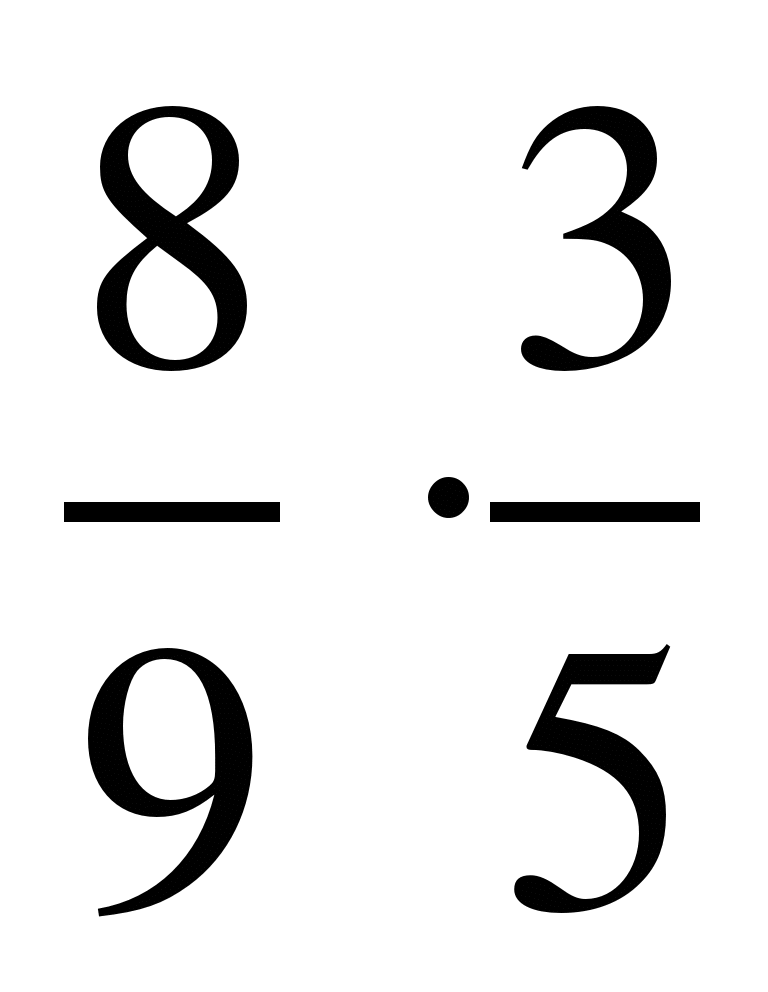 ; 8)
; 8) 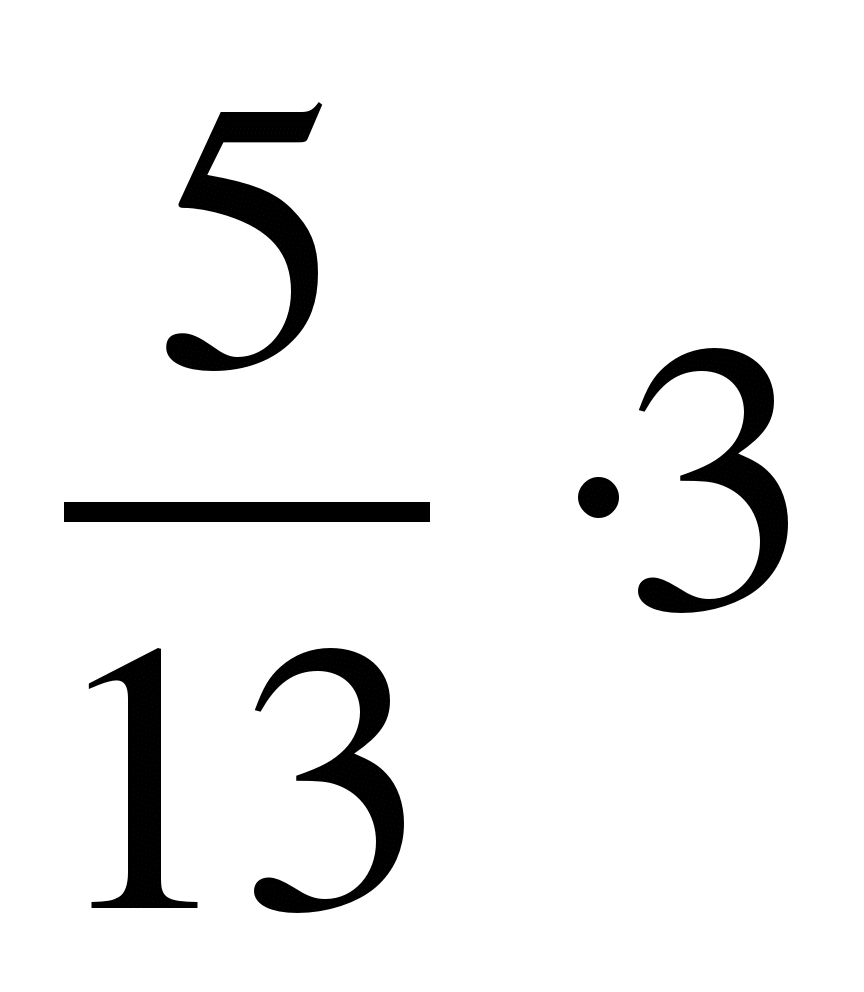 ;
;
9) 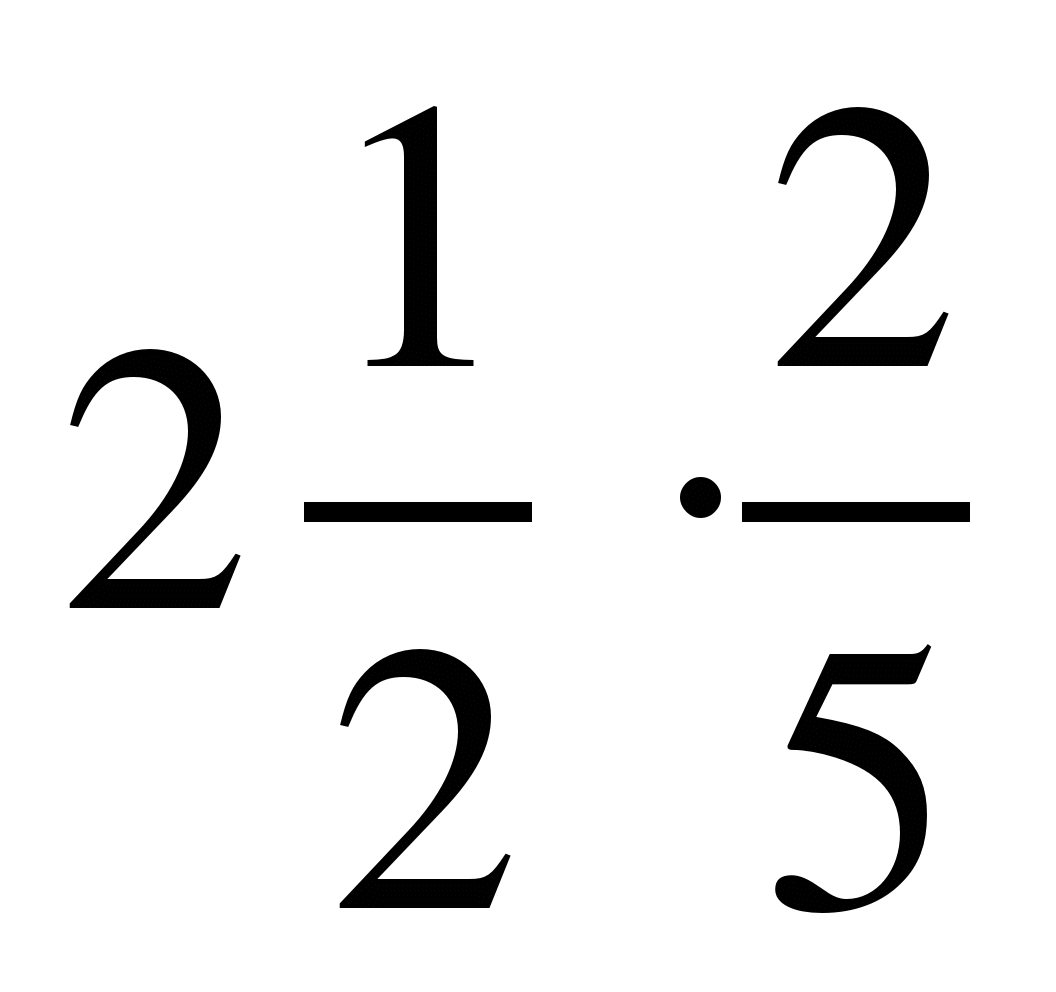 ; 10)
; 10) 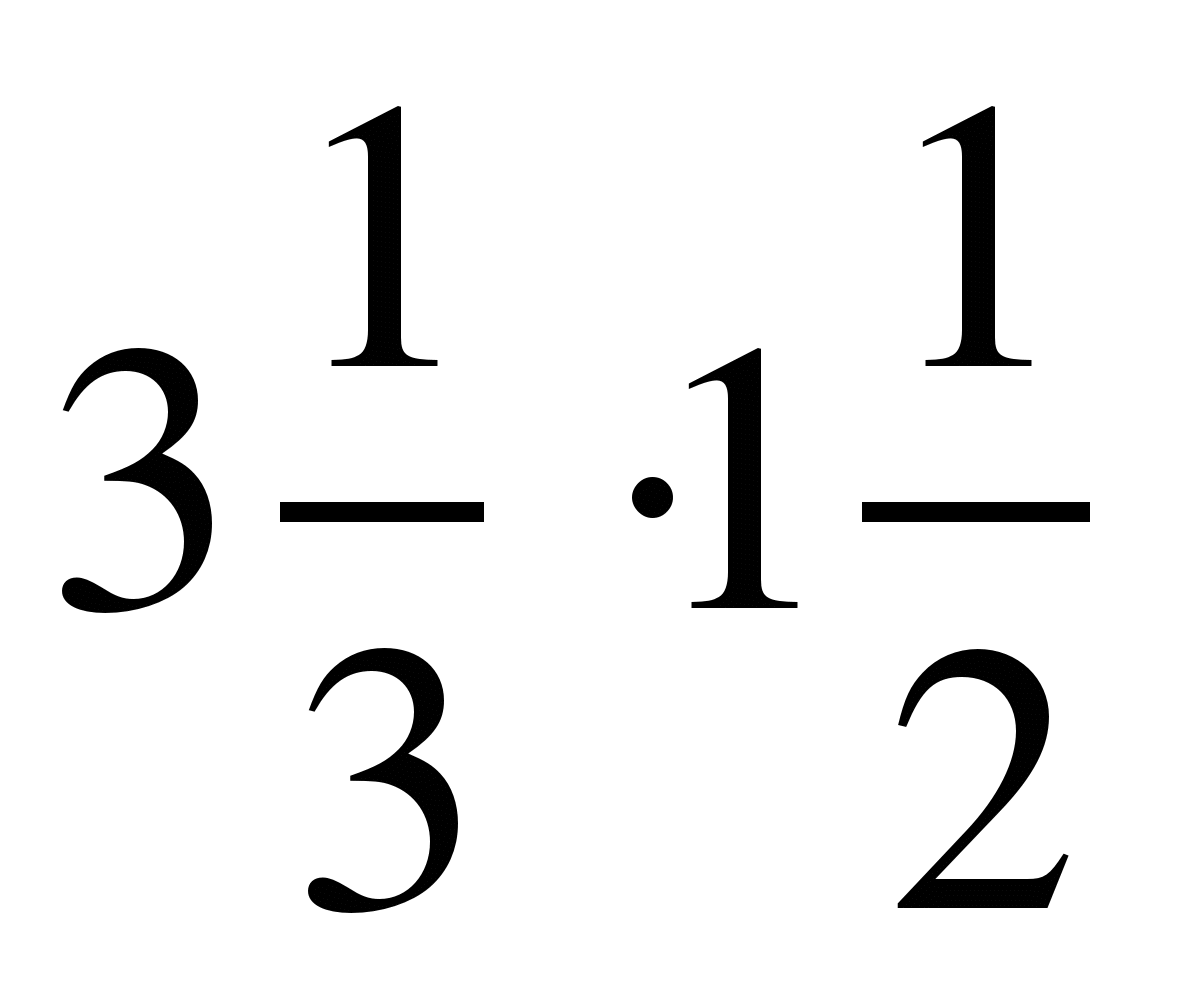 ;
;
Деление дробей.
Умножь числитель на знаменатель и знаменатель на числитель:
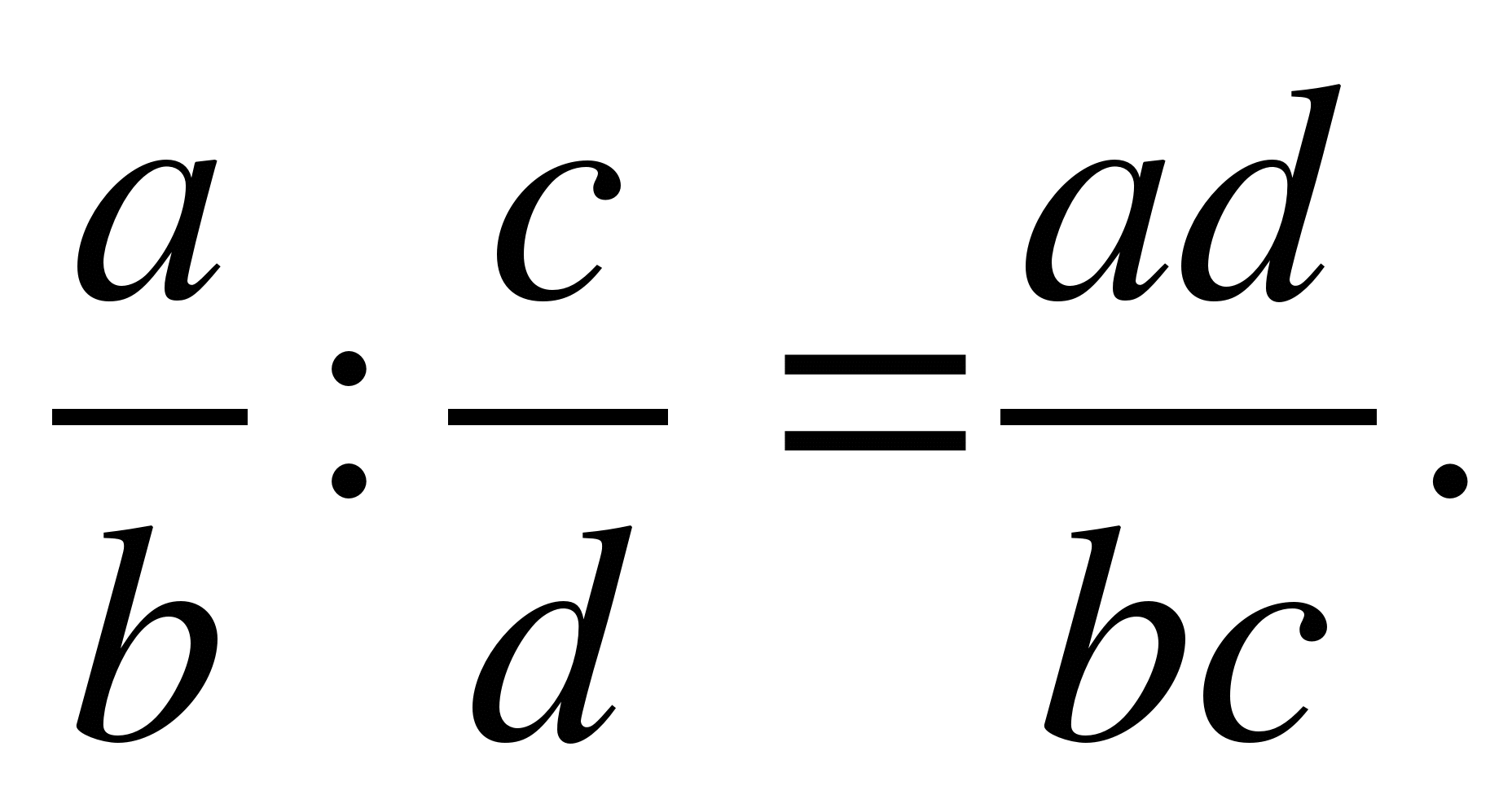
1)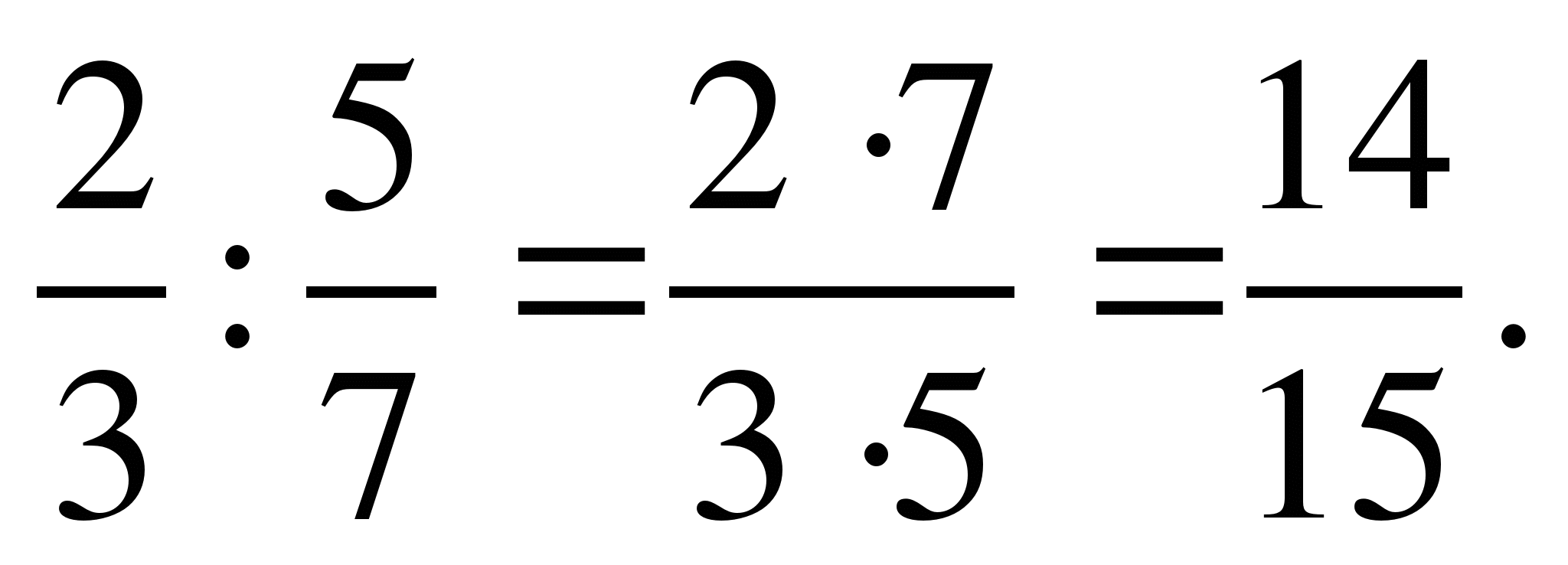
2) 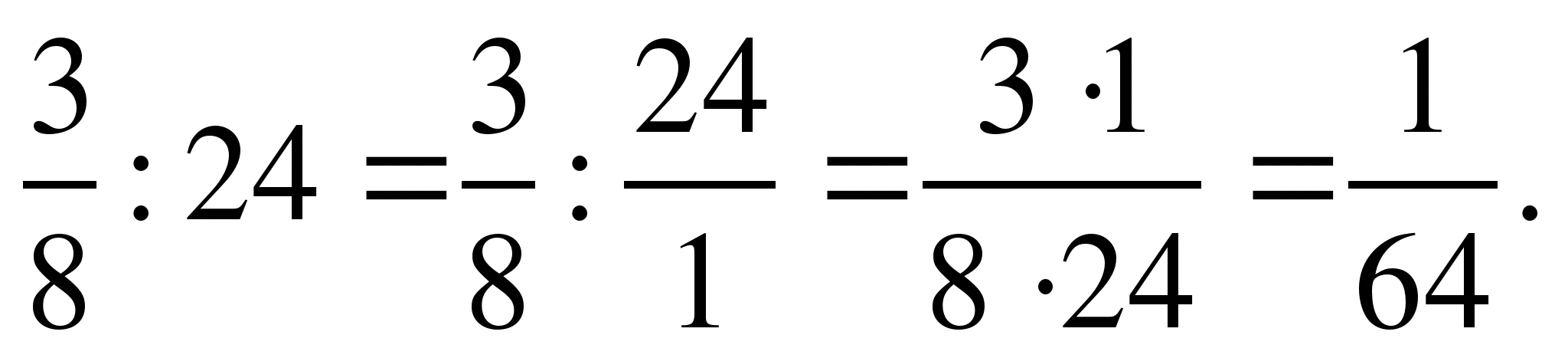
3) 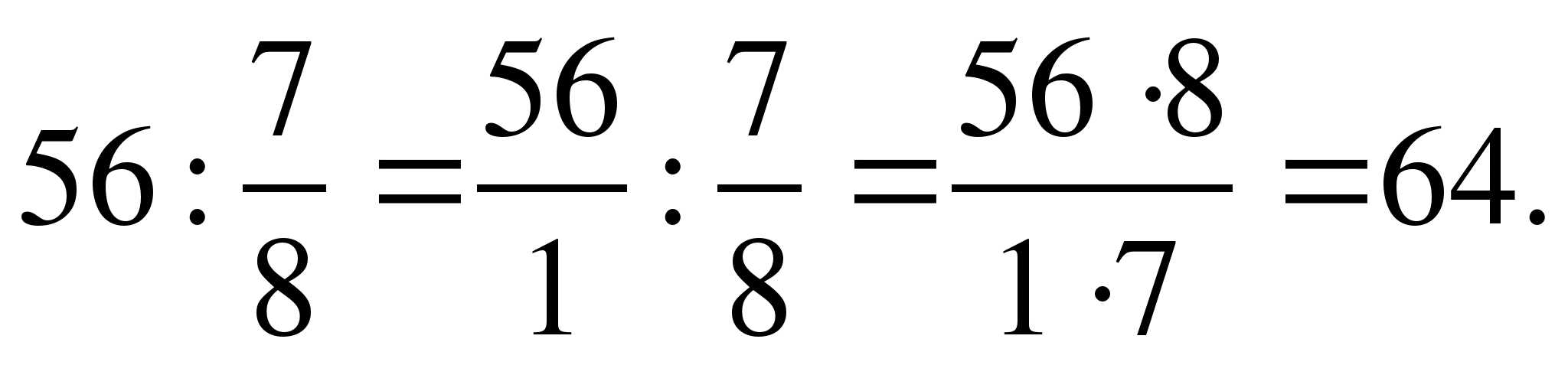
4)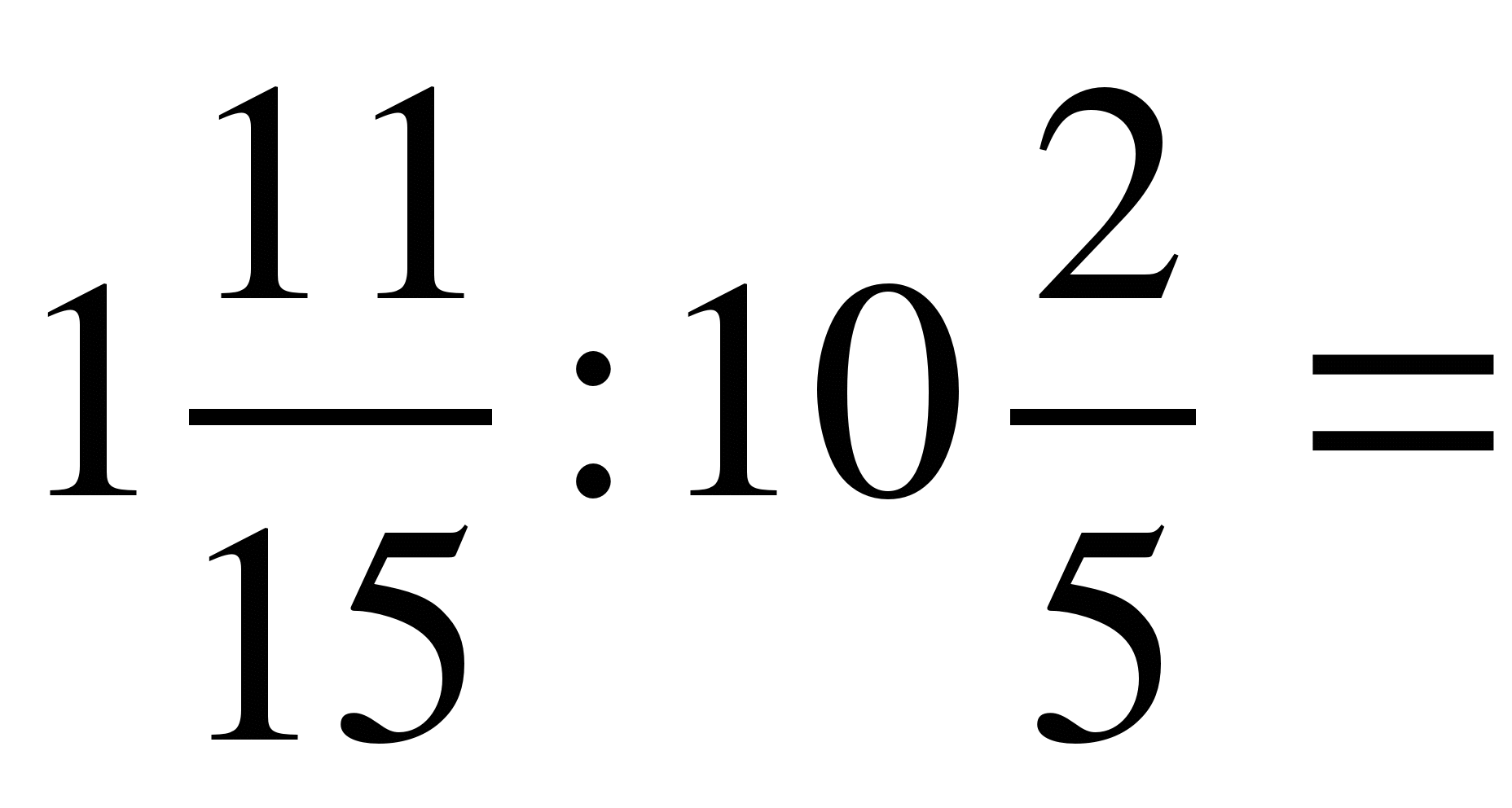
=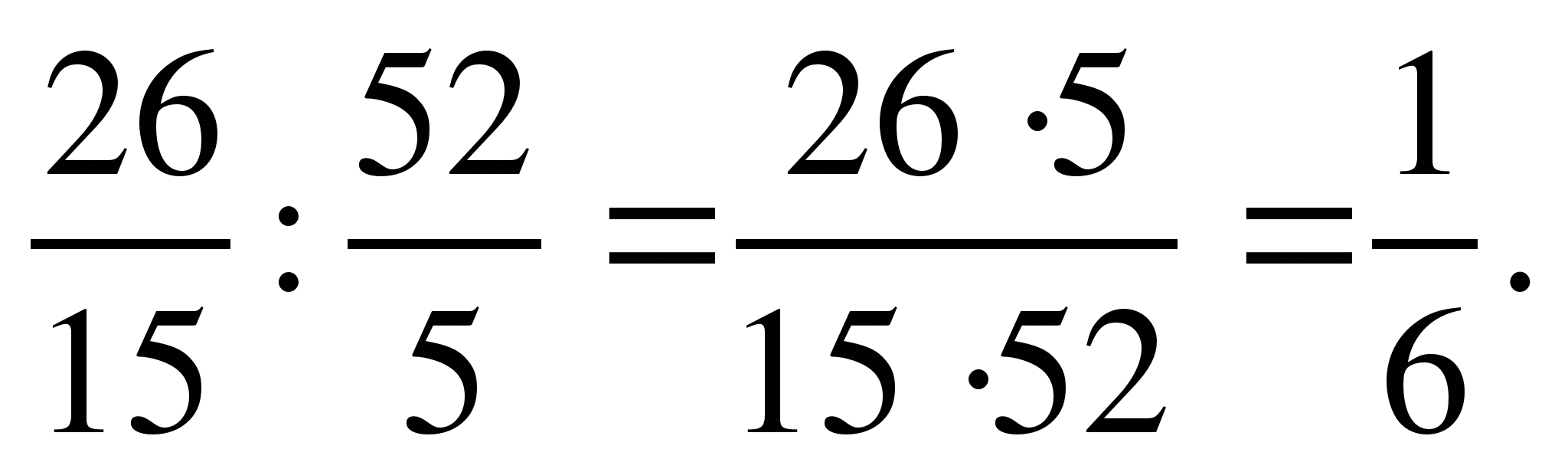
5)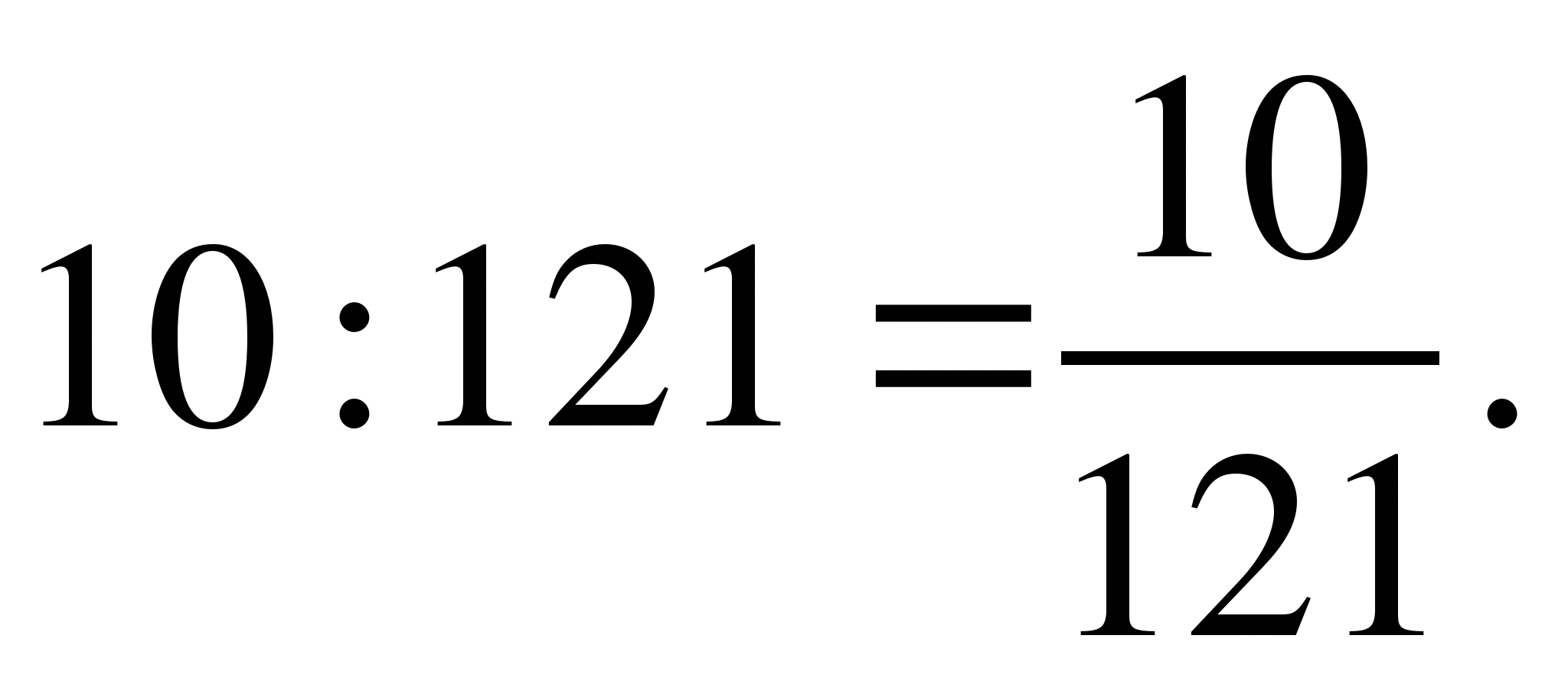
Найдите частное дробей:
1)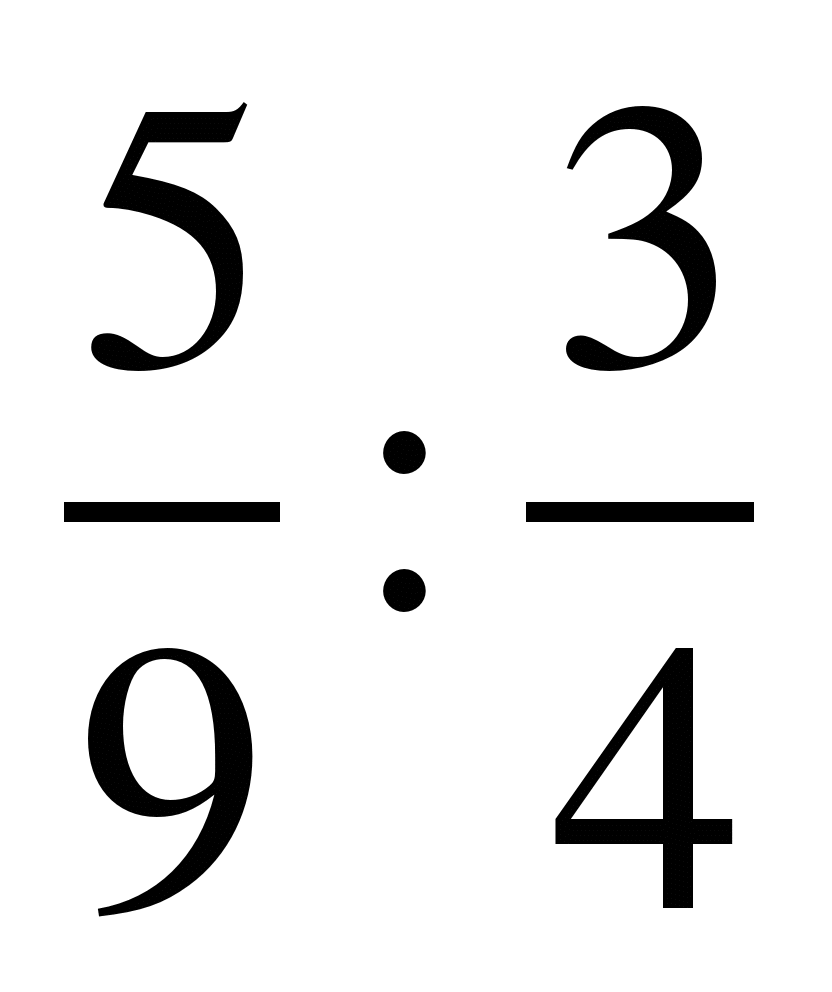 ; 2)
; 2) 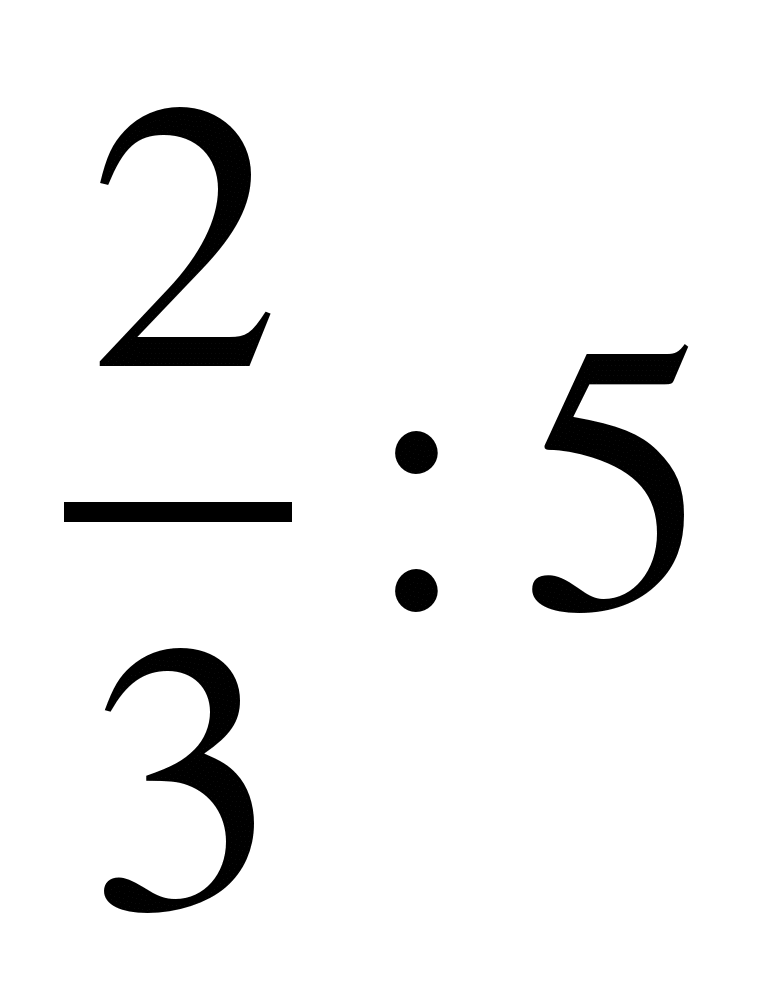 ; 3)
; 3) 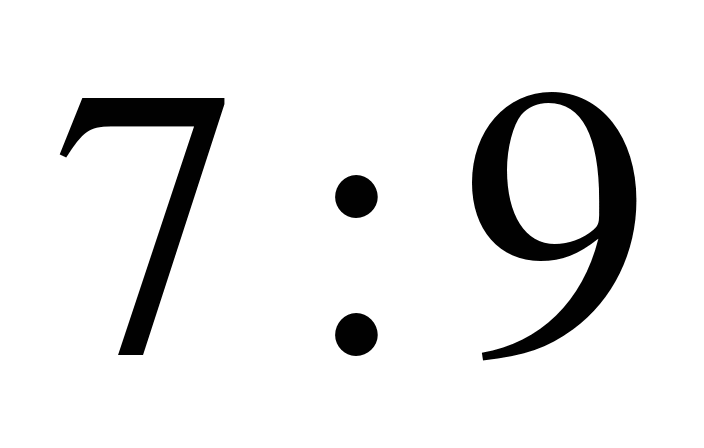 ; 4)
; 4) 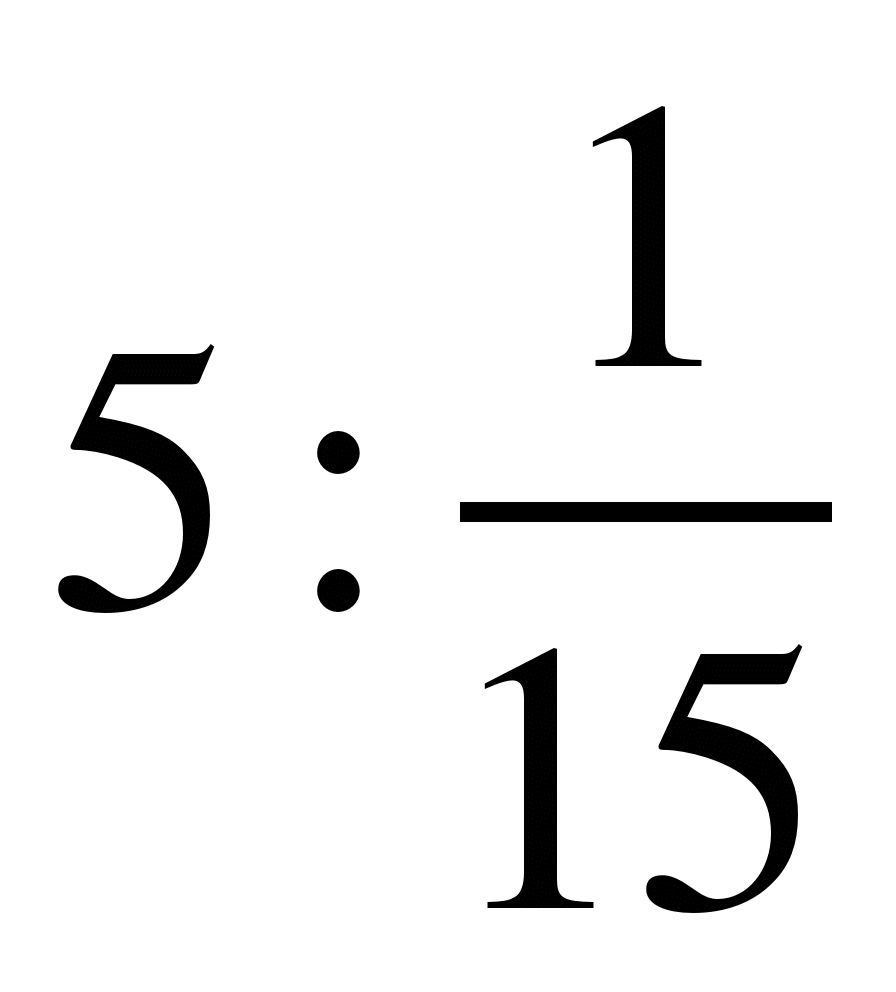 ; 5)
; 5) 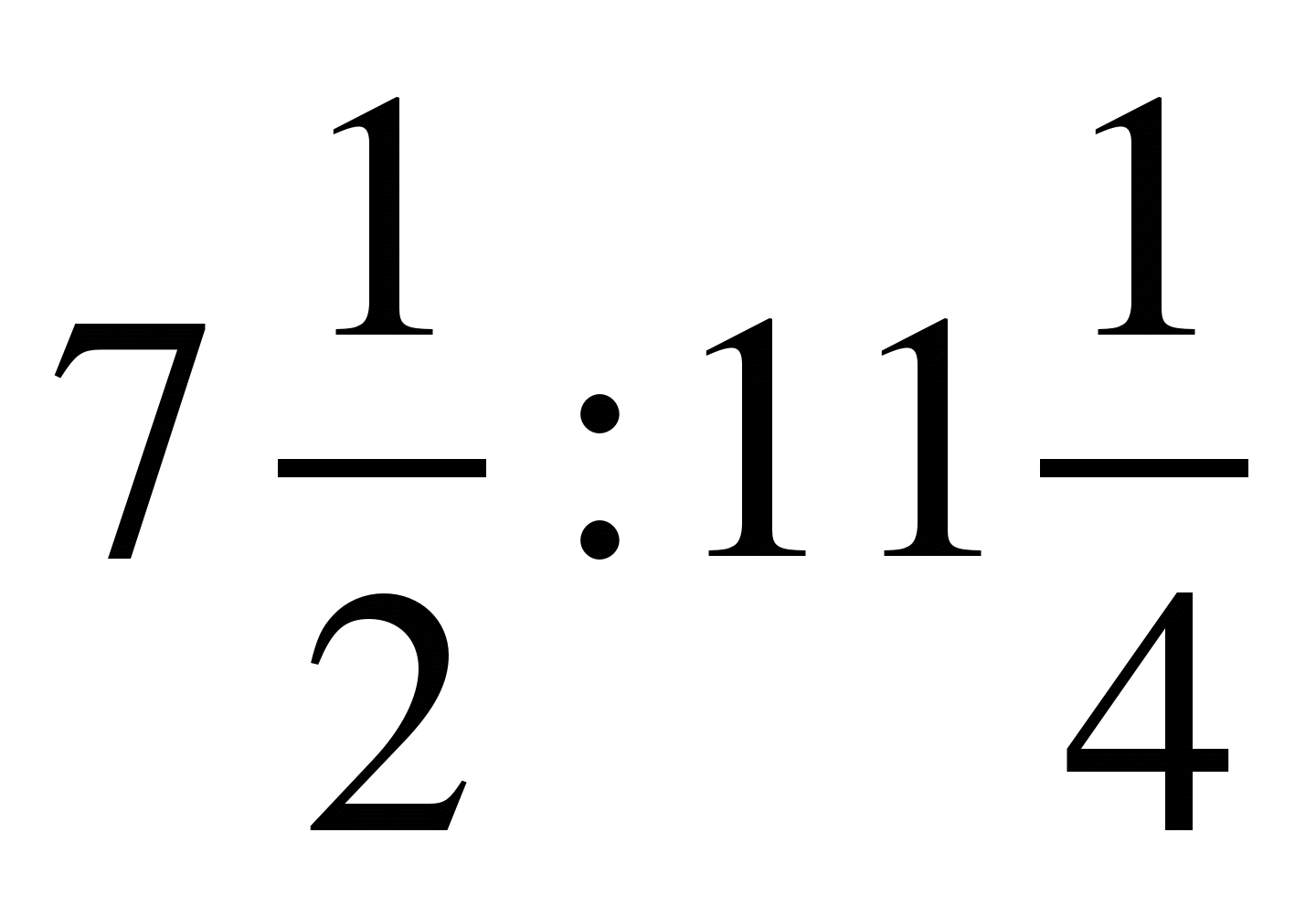 ; 6)
; 6) 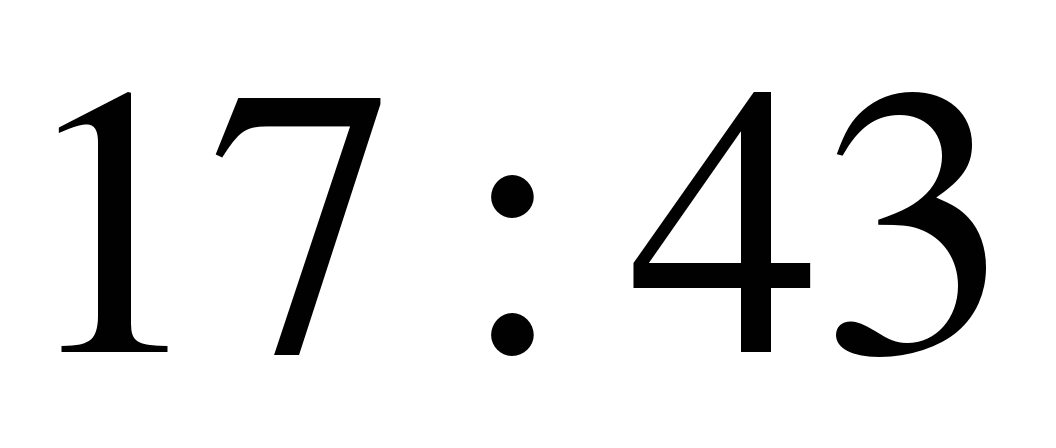 ;
;
7) 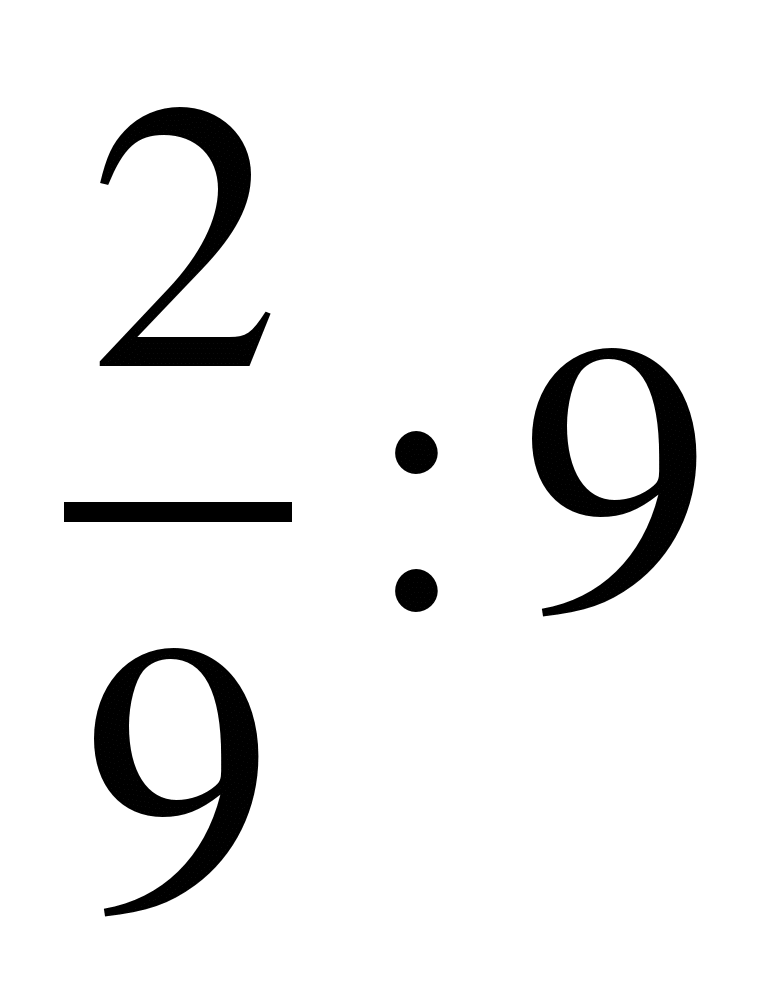 ; 8)
; 8) 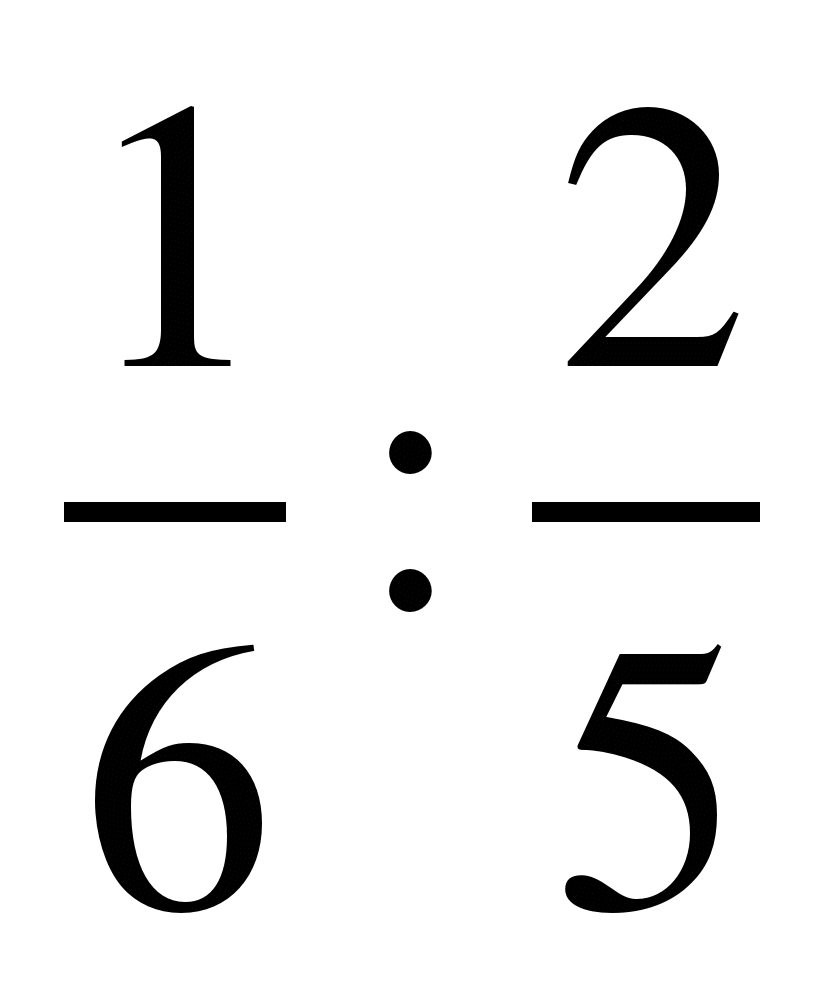 ; 9)
; 9) 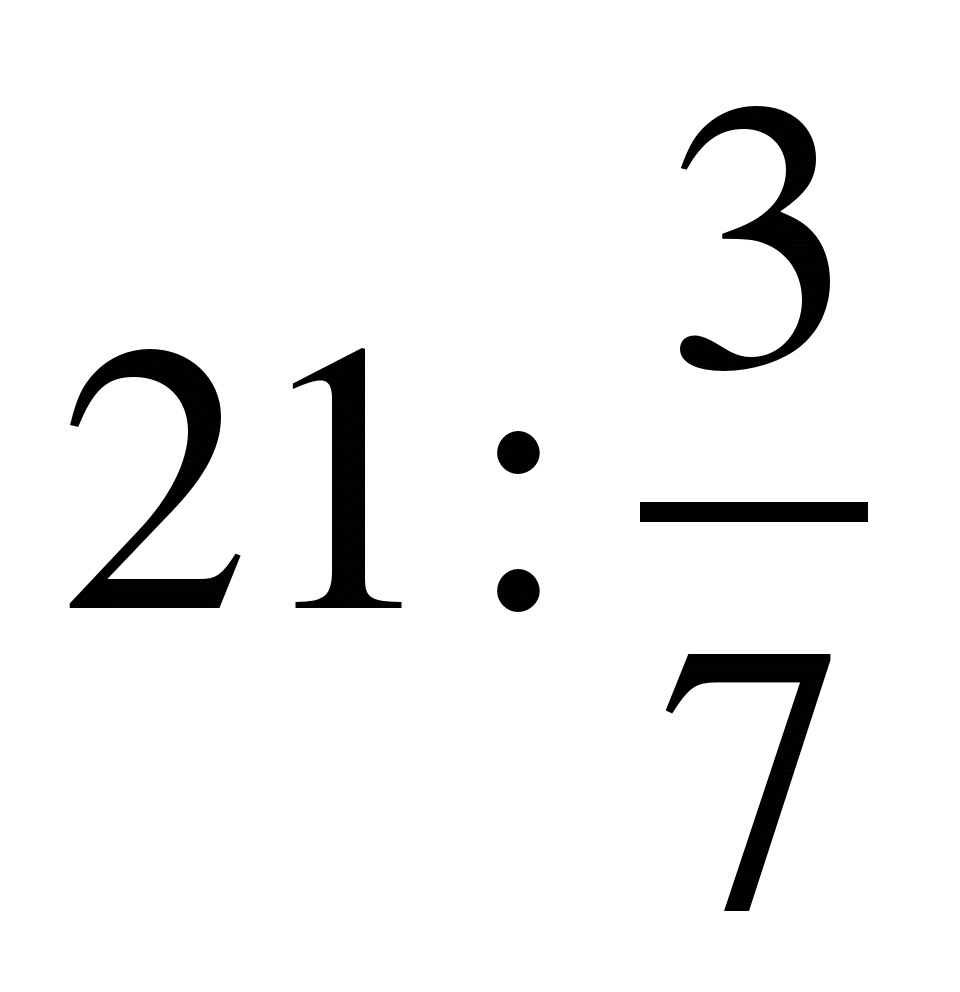 ; 10)
; 10) 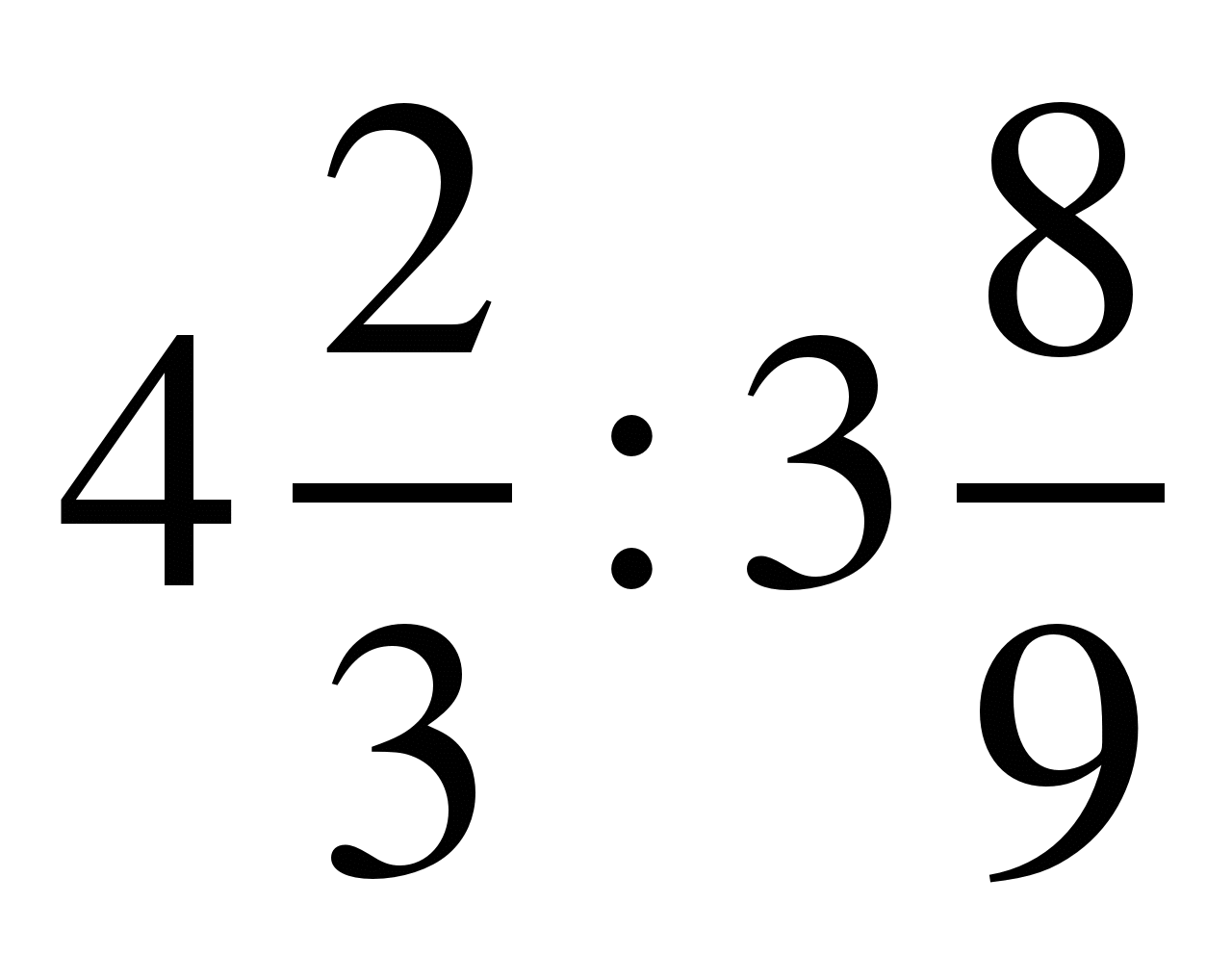 ; 11)
; 11) 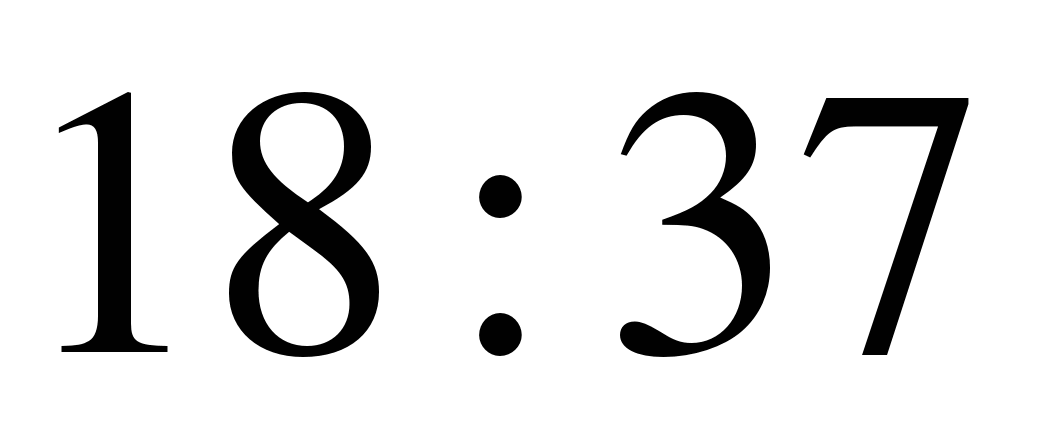 ; 12)
; 12) 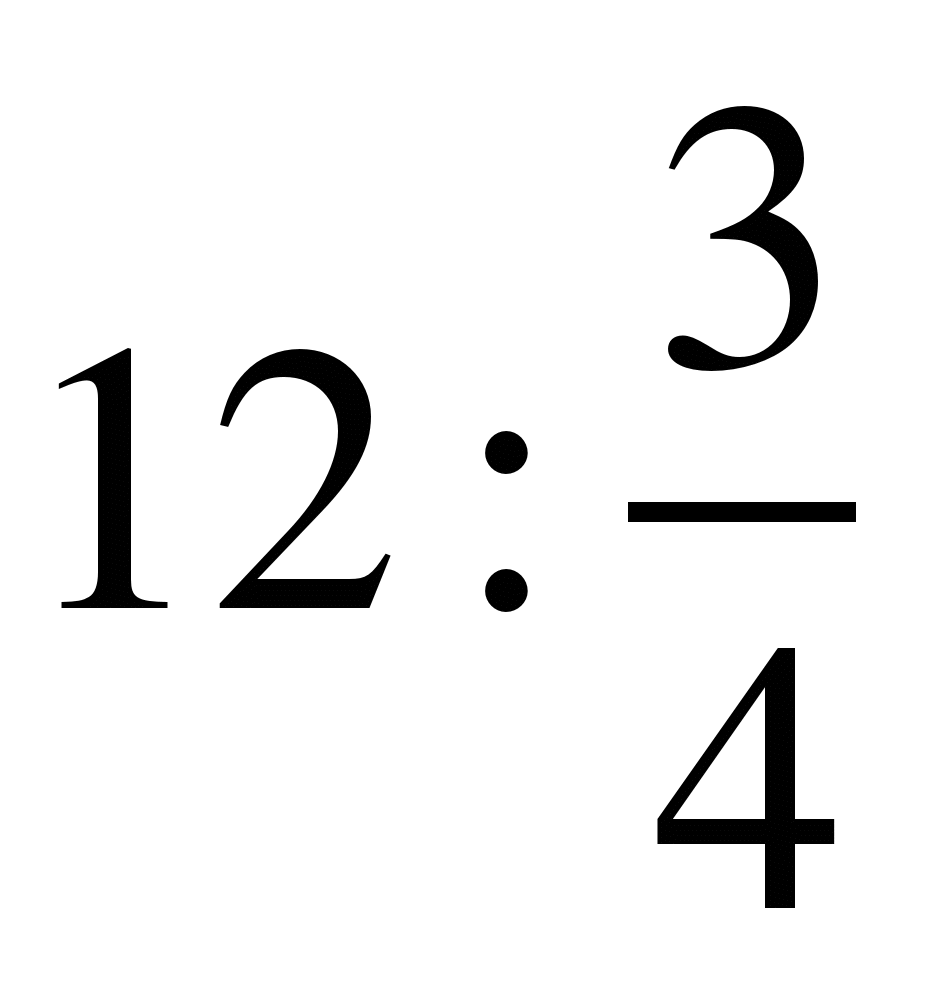 ;
;
13) 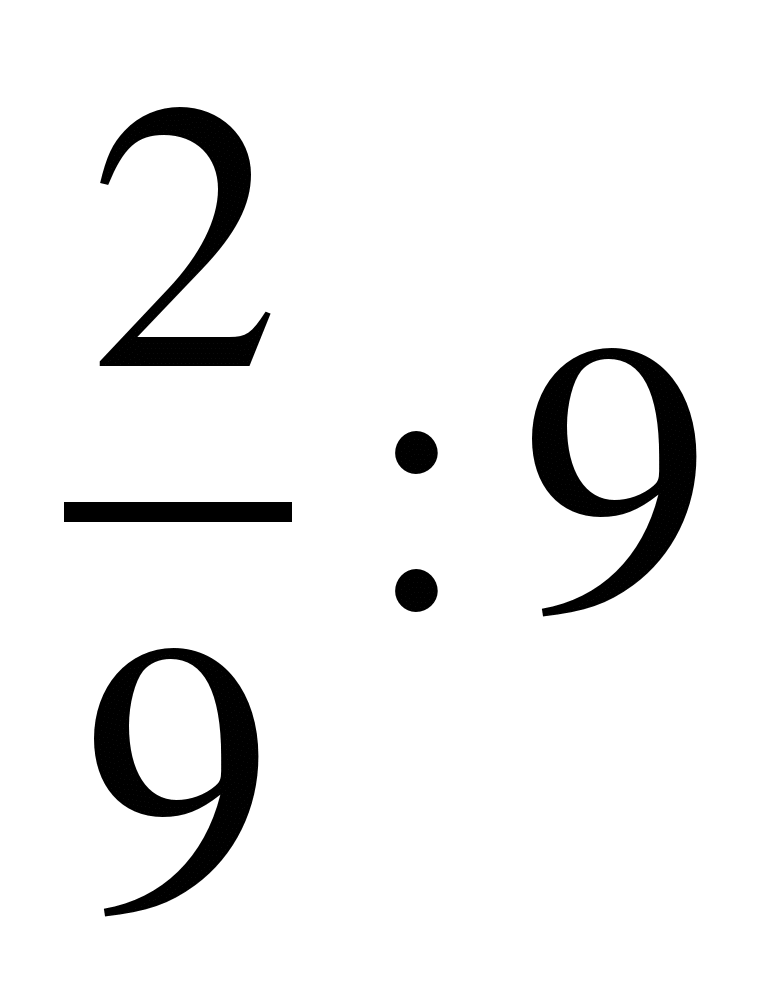 ; 14)
; 14) 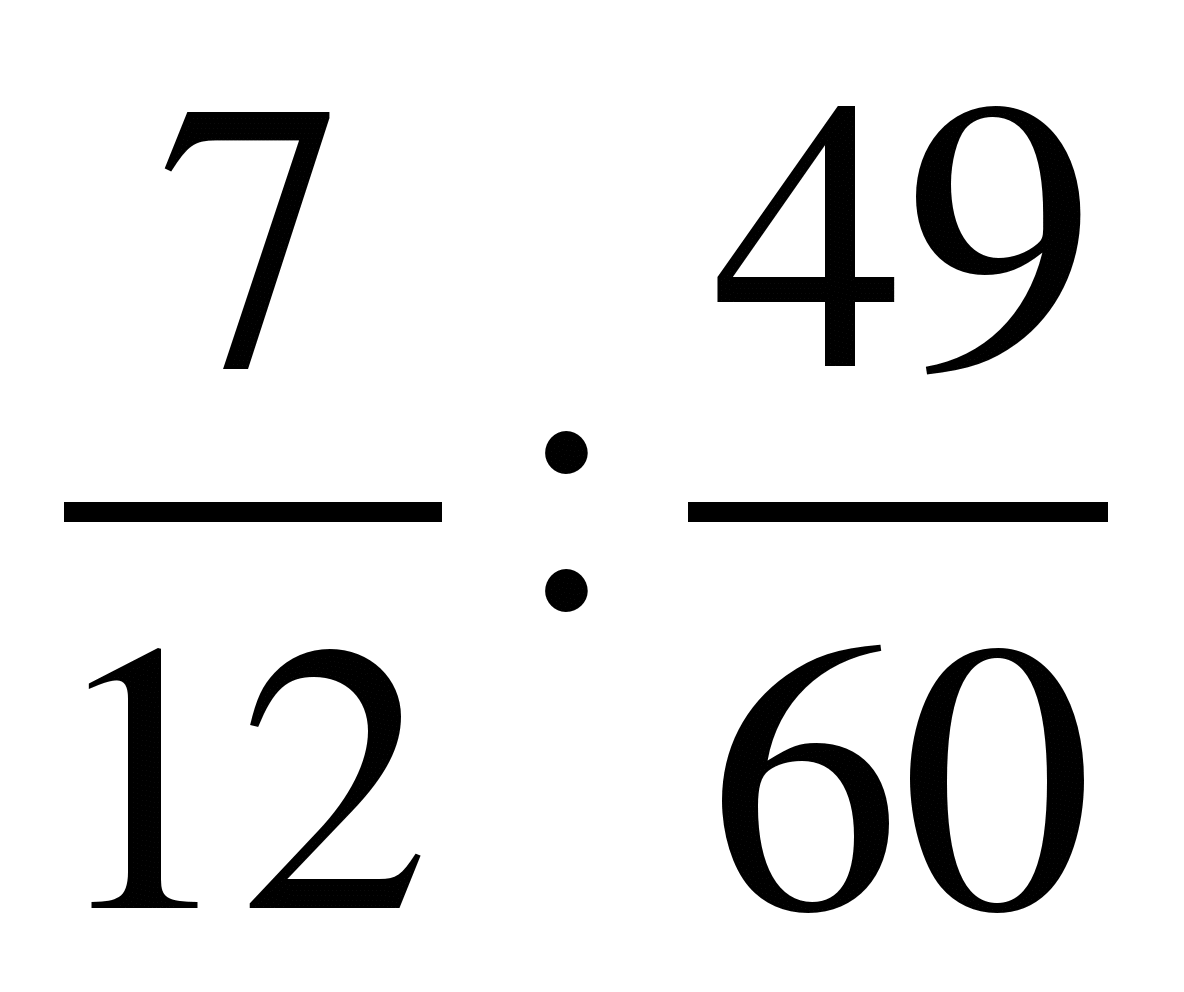 .
.
Основное свойство пропорции.
Неизвестный крайний член пропорции равен произведению ее средних членов, деленному на известный крайний.
Неизвестный средний член пропорции равен произведению ее крайних членов, деленному на известный средний.
Проверить пропорцию
0,9 : 3 = 0,3 : 1.
Решение:
0,9 1 = 0,9, 3 × 0,3 = 0,9.
Решить уравнение:
а) х : 7 = 18 : 14;
б) 25 : 75 = 2 : х.
Решение:
а) х = 7 × 18 : 14 = 9;
б) х = 75 × 2 : 25 = 6.
Решить уравнение:
а) 24 : х = 8 : 13;
б) 6 : 2 = х : 70.
Решение:
а) х = 24 × 13 : 8 = 39;
б) х = 6 × 70 : 2 = 210.
1) Проверить пропорцию:
1 : 2 = 0,2 : 0,4.
Решить уравнения:
2) х : 7 = 9 : 2;
3) 5 : 3 = t : 6;
4) 1 : 3 = x : 18;
5) 5 : 4 = 25 : y.
6) Проверить пропорцию
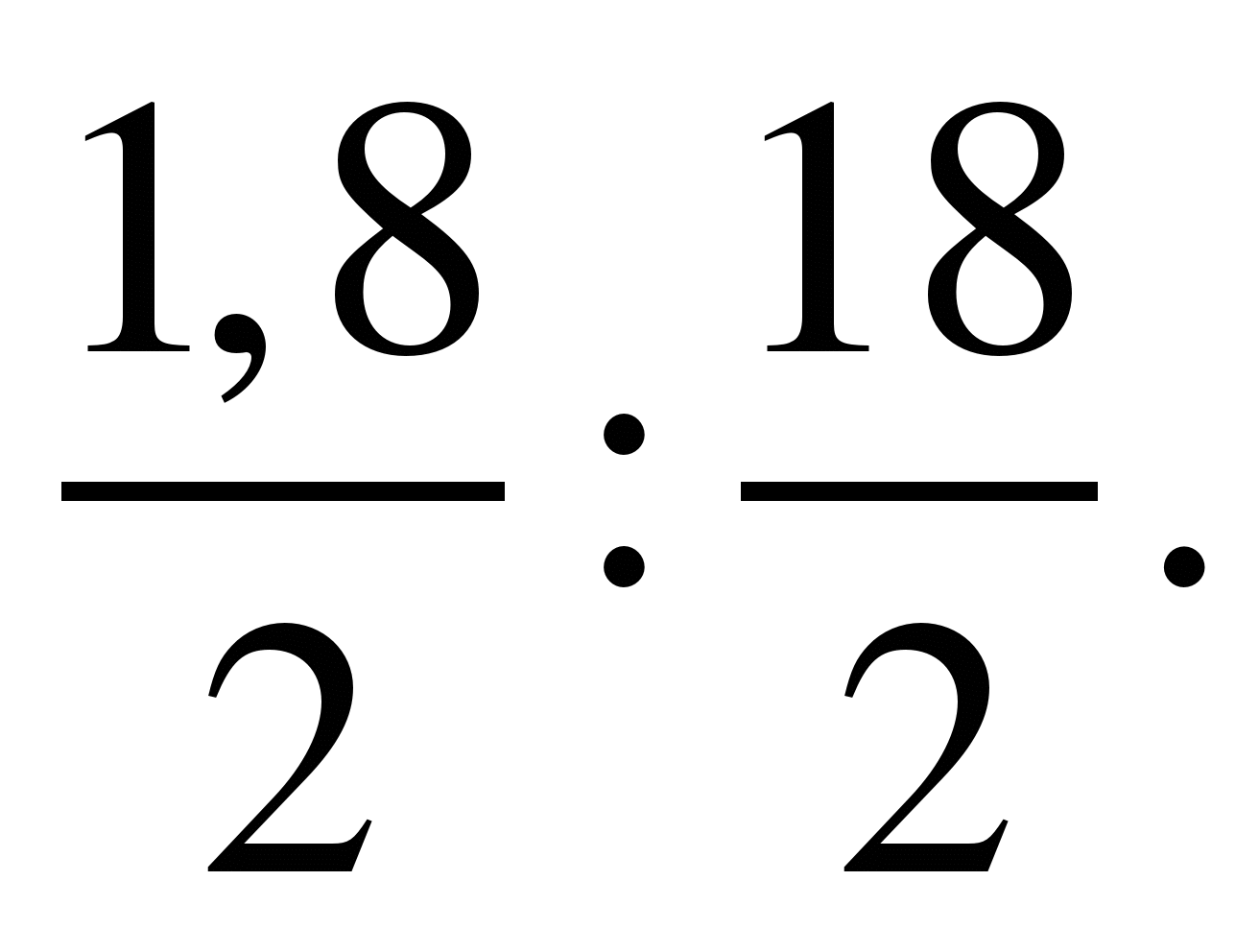
Решить уравнения:
7) 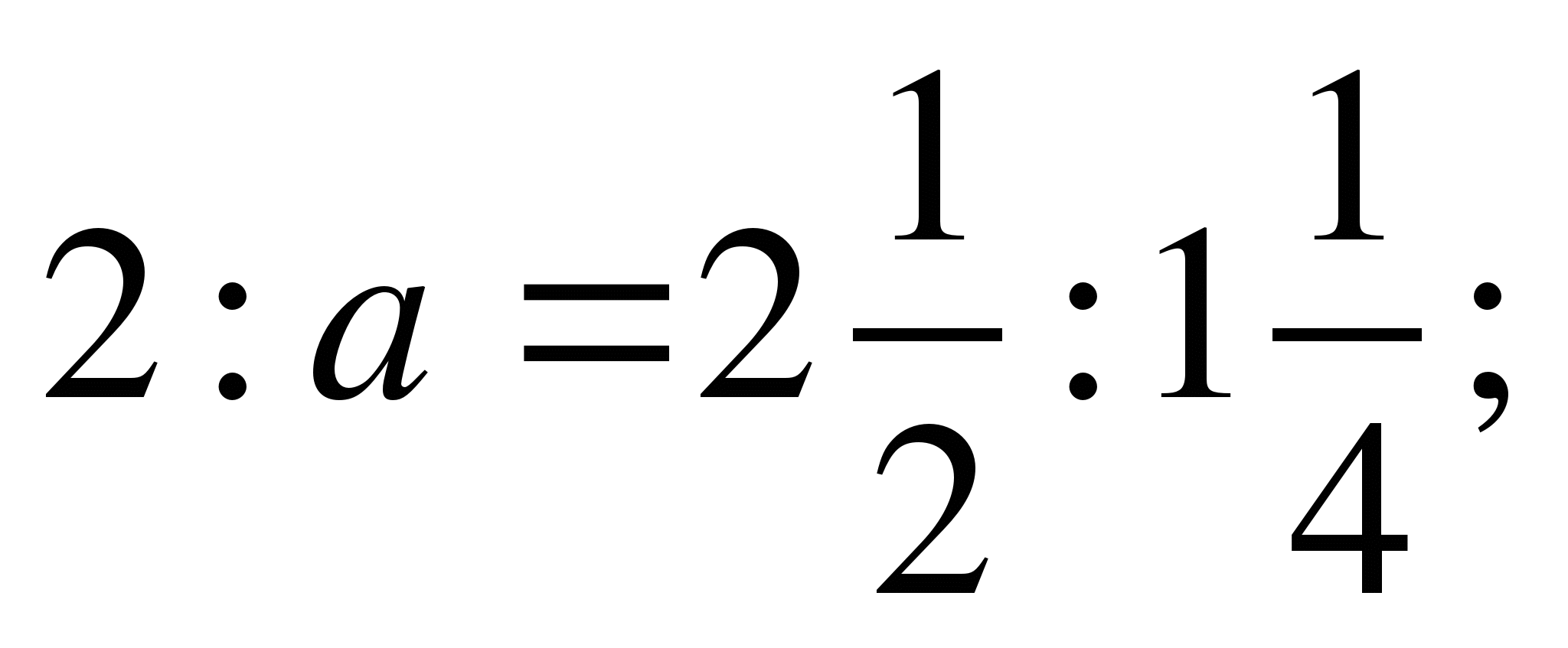
8) 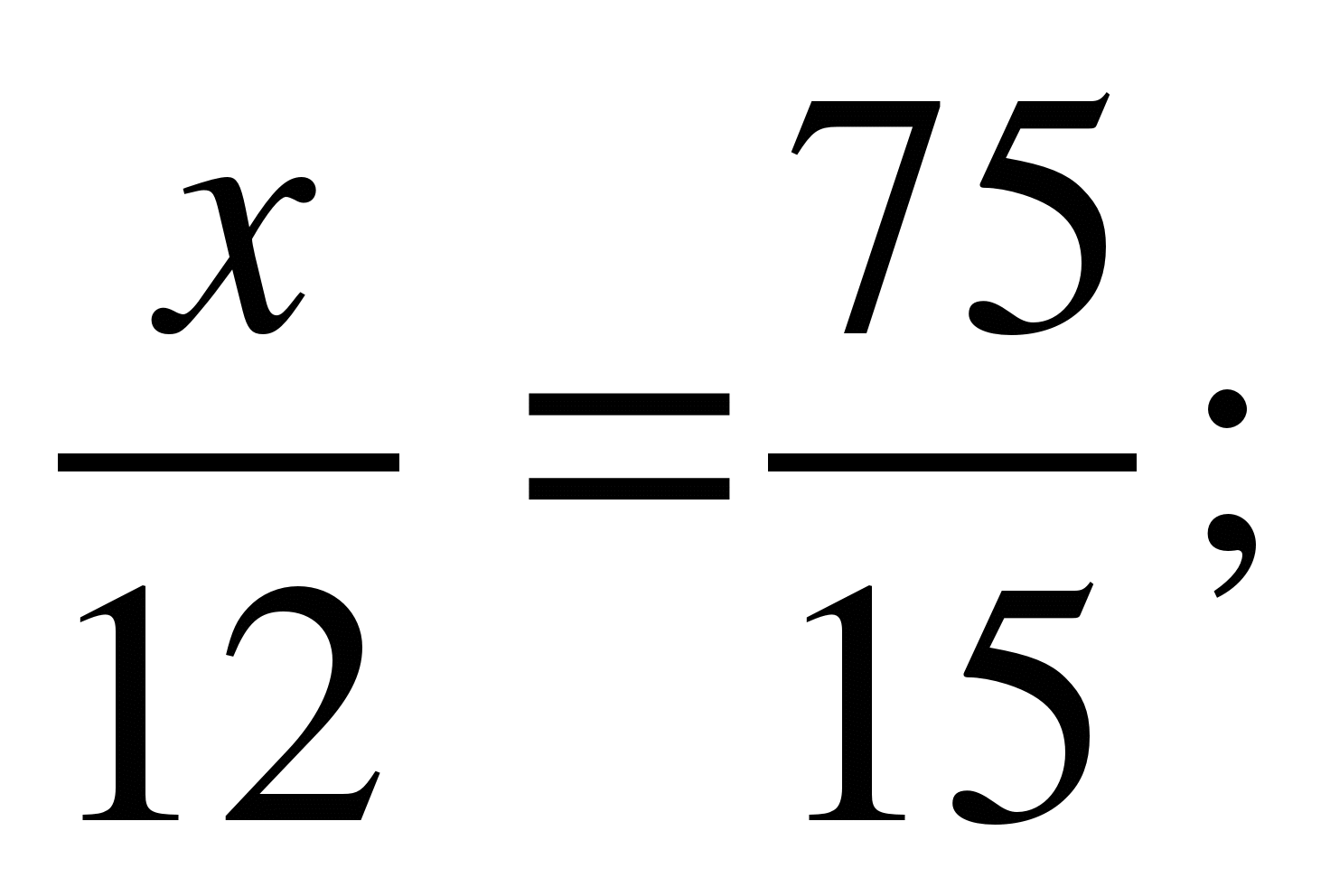
9) 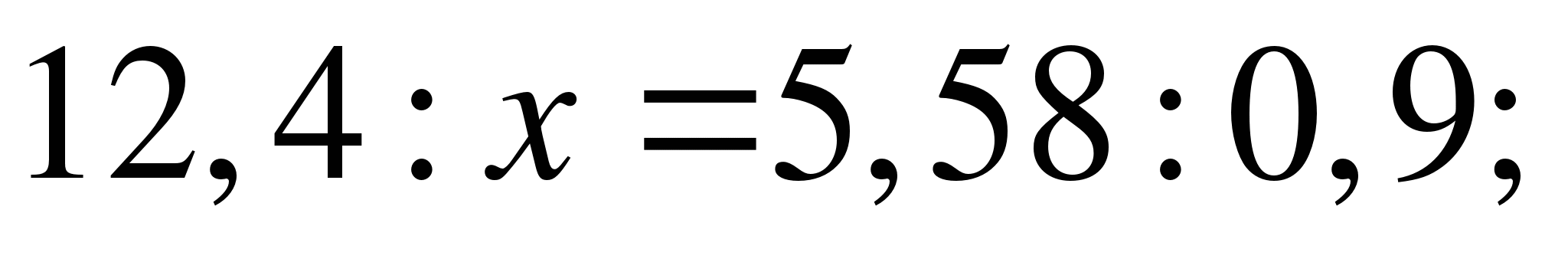 ;
;
10) 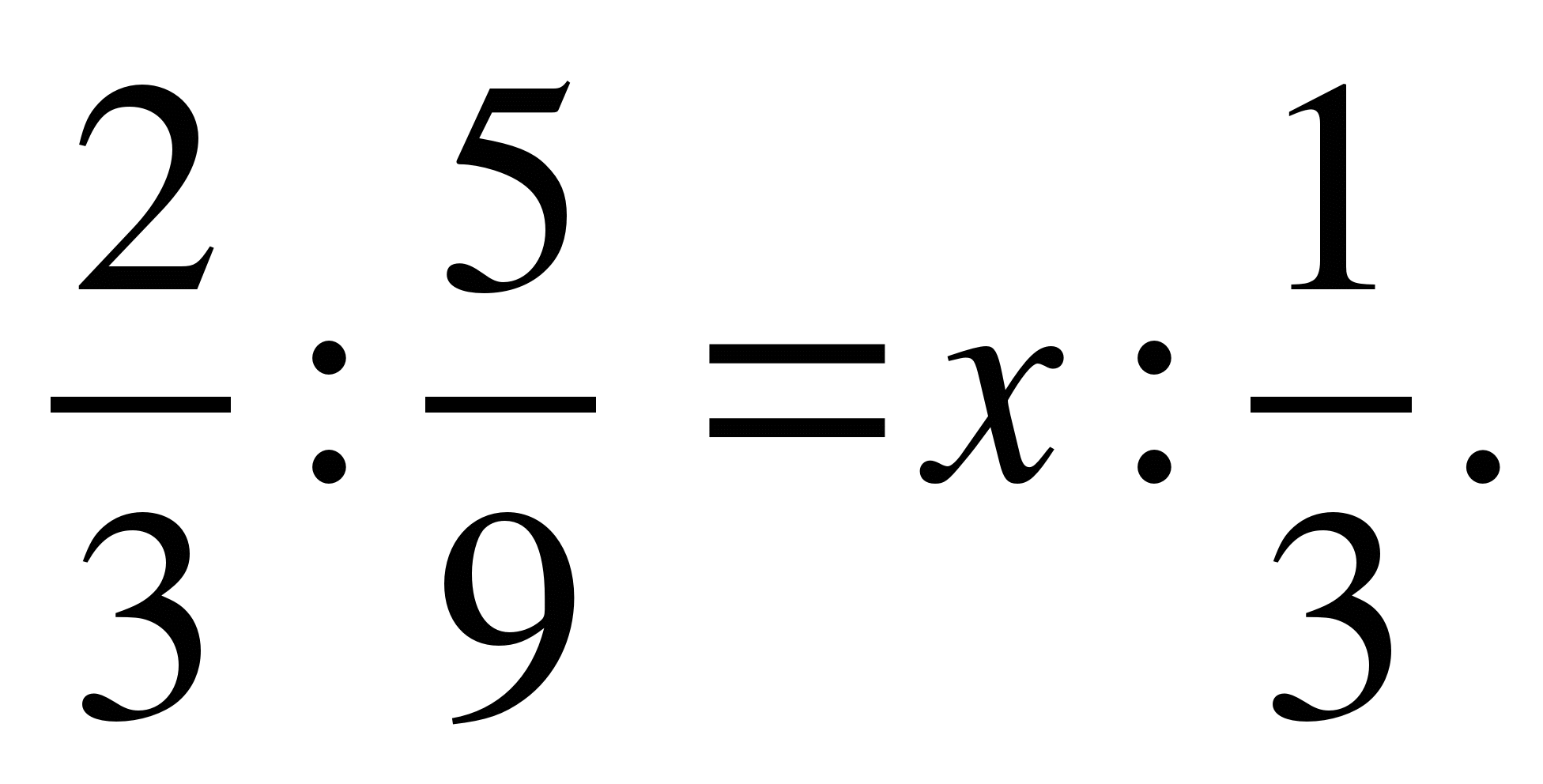 ;
;
11) Проверить пропорцию:
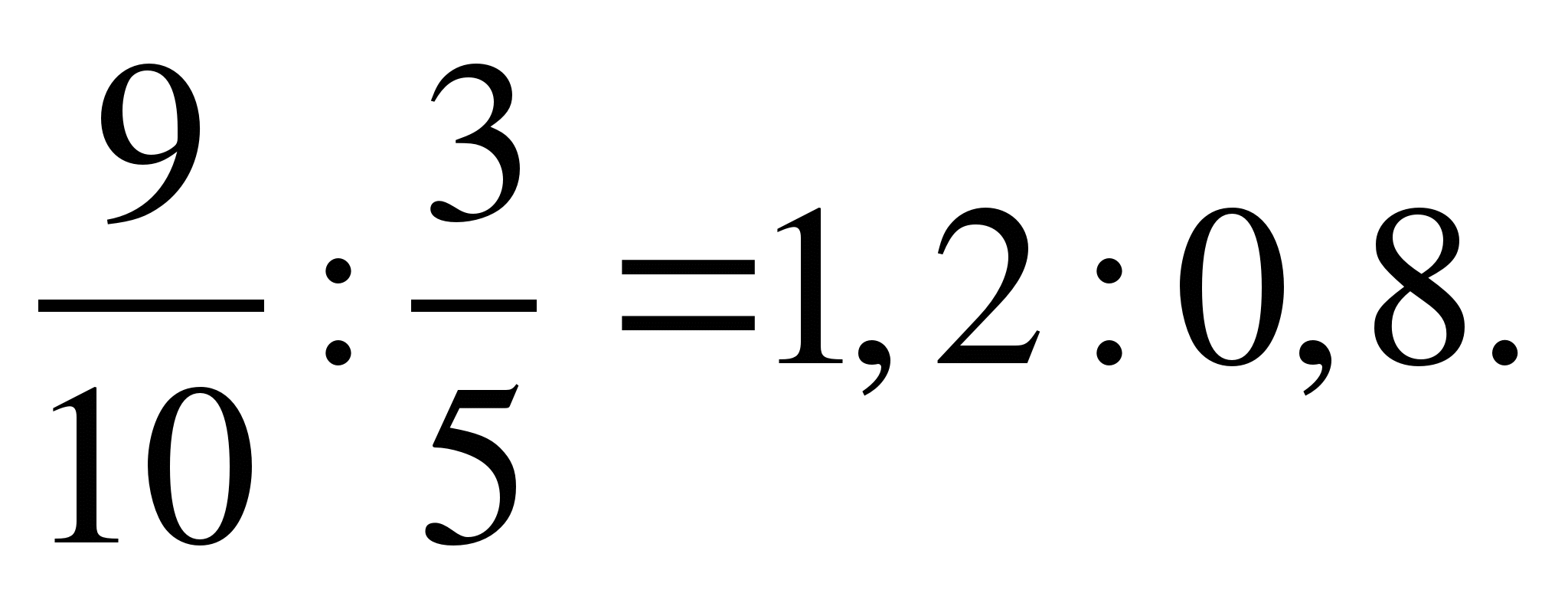
Решить уравнения:
12) 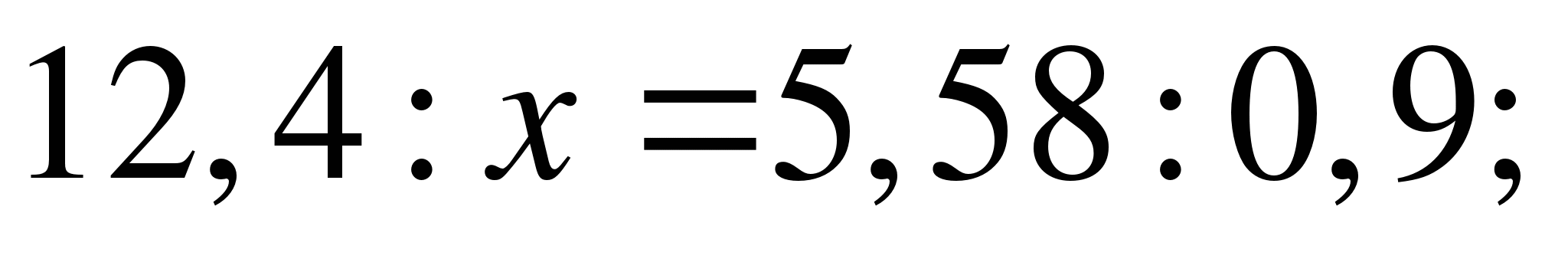 ;
;
13) 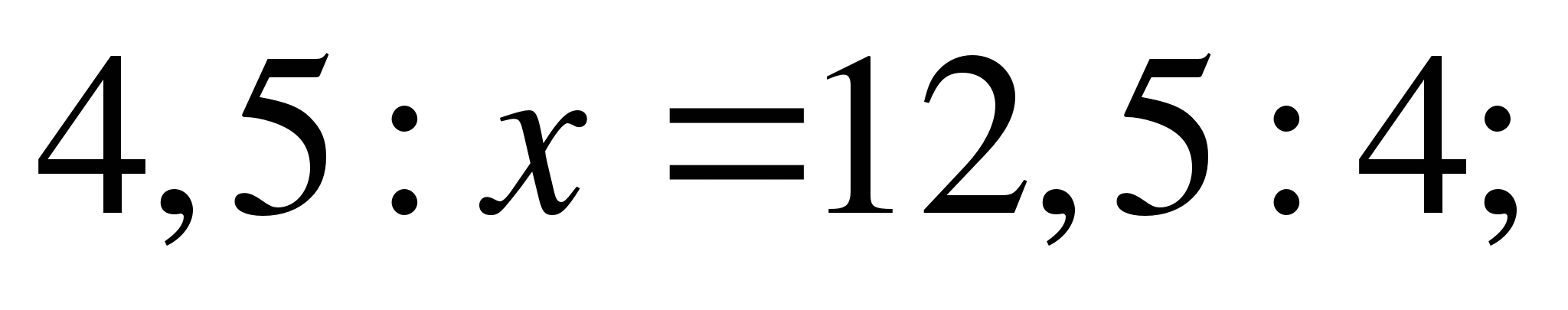 ;
;
14) 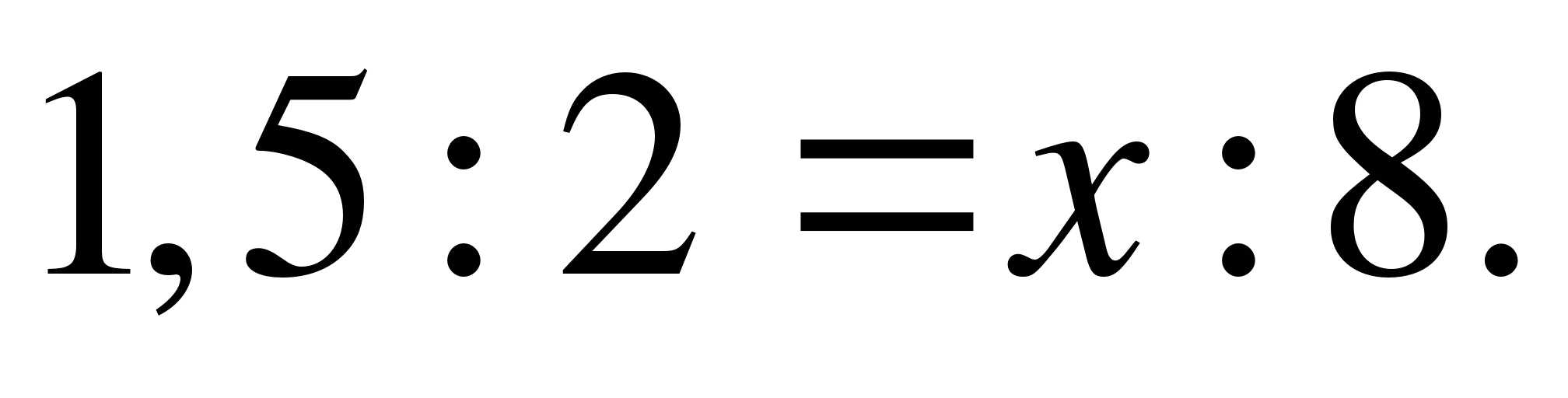
Смешанные числа.
правильной, если знаменатель больше числителя.
Дробь называется неправильной, если знаменатель меньше числителя.
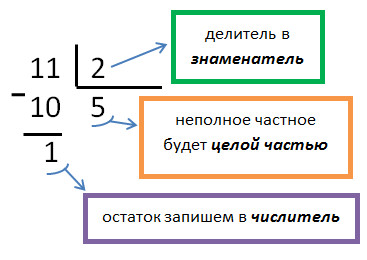
Чтобы неправильную дробь представить в виде смешанного числа, нужно числитель разделить на знаменатель.
Чтобы смешанное число представить в виде неправильной дроби нужно:
смешанное число
неправильная дробь
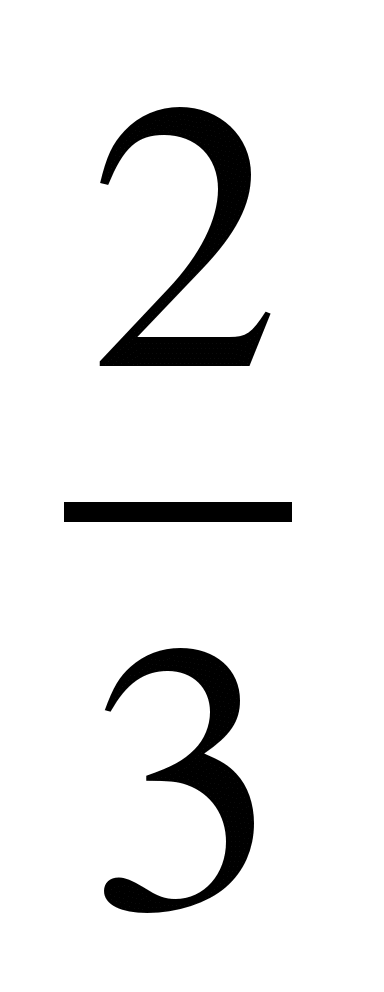 – правильная дробь.
– правильная дробь.
 – неправильная дробь.
– неправильная дробь.
1) Выделить целую часть из дроби .
.
Решение:
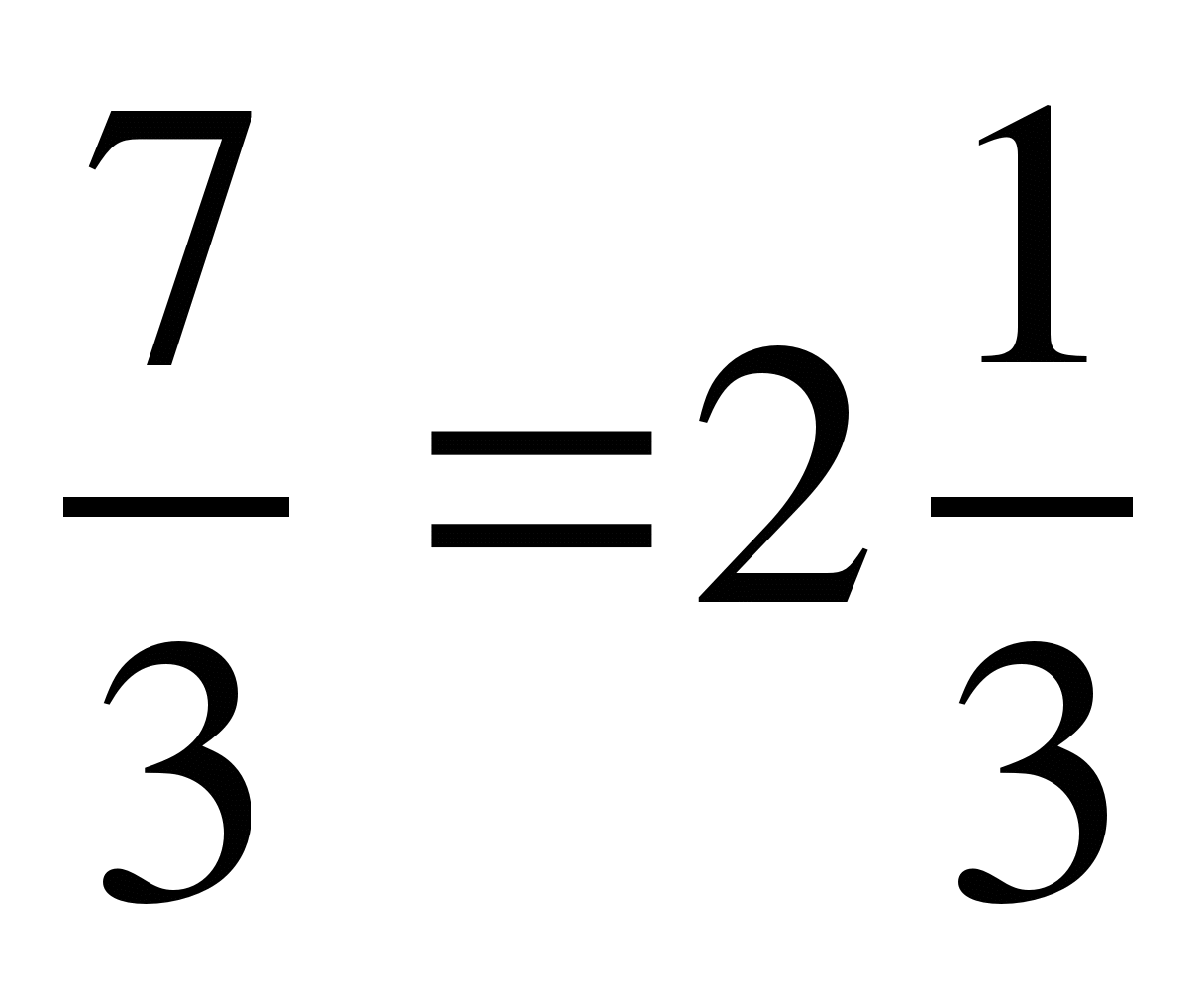
целая часть
1 – остаток от деления =
числитель
2) Записать число 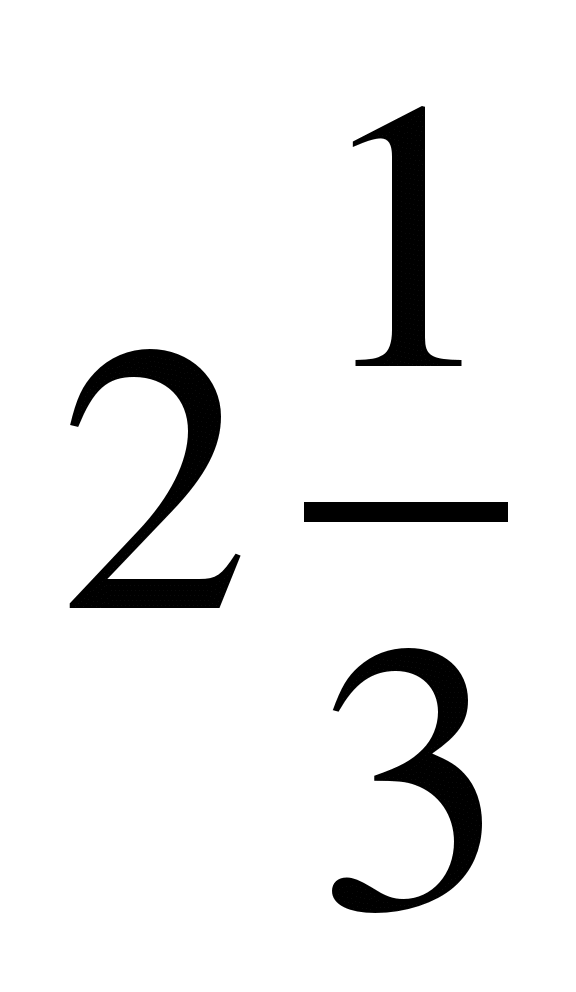 в виде неправильной дроби.
в виде неправильной дроби.
Решение:
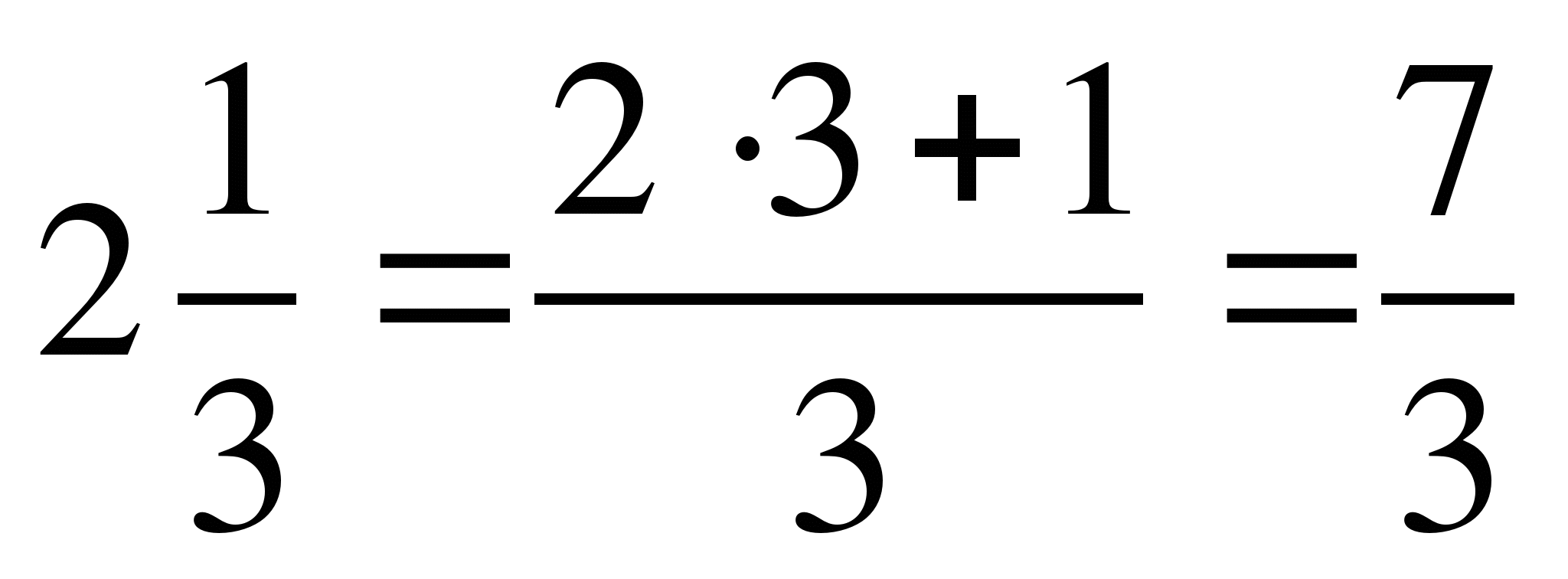
Выделите целую часть числа:
1)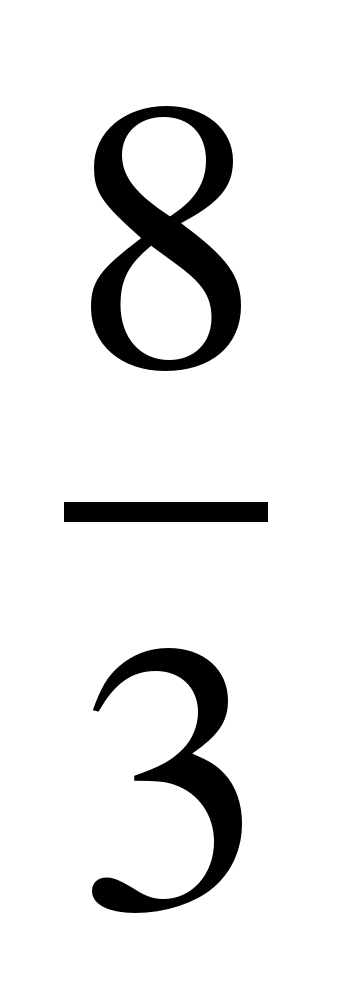 ; 2)
; 2) ;
;
3)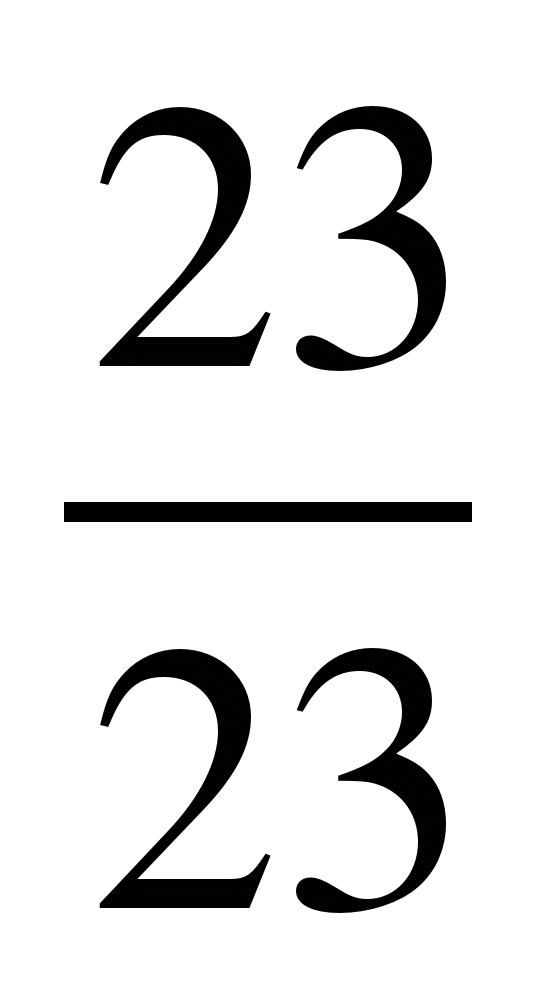 ; 4)
; 4)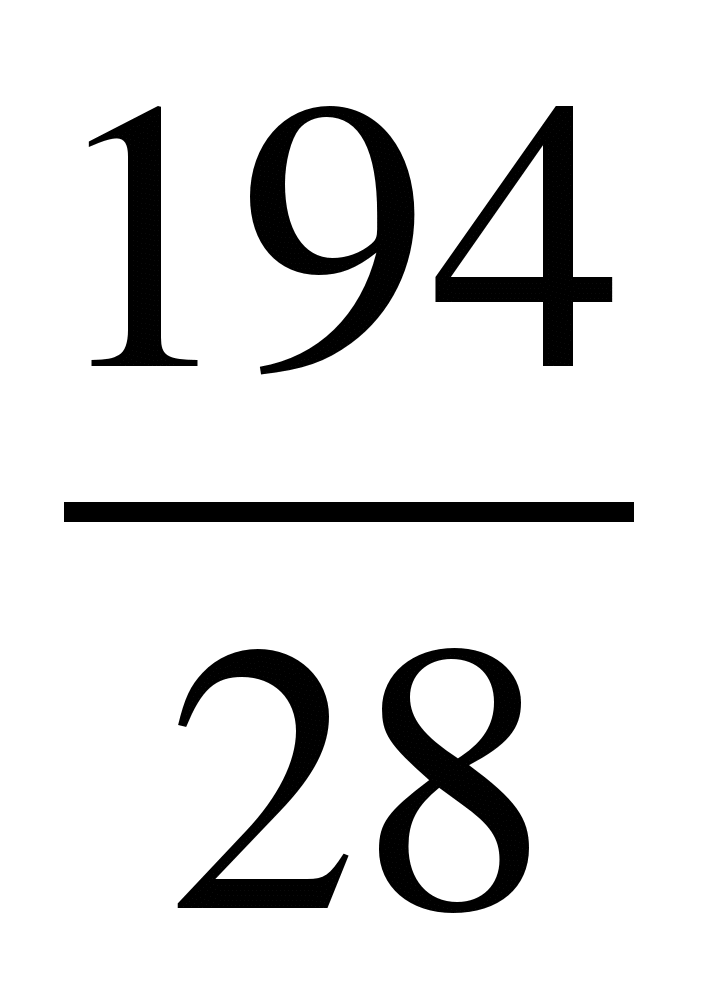 ;
;
5)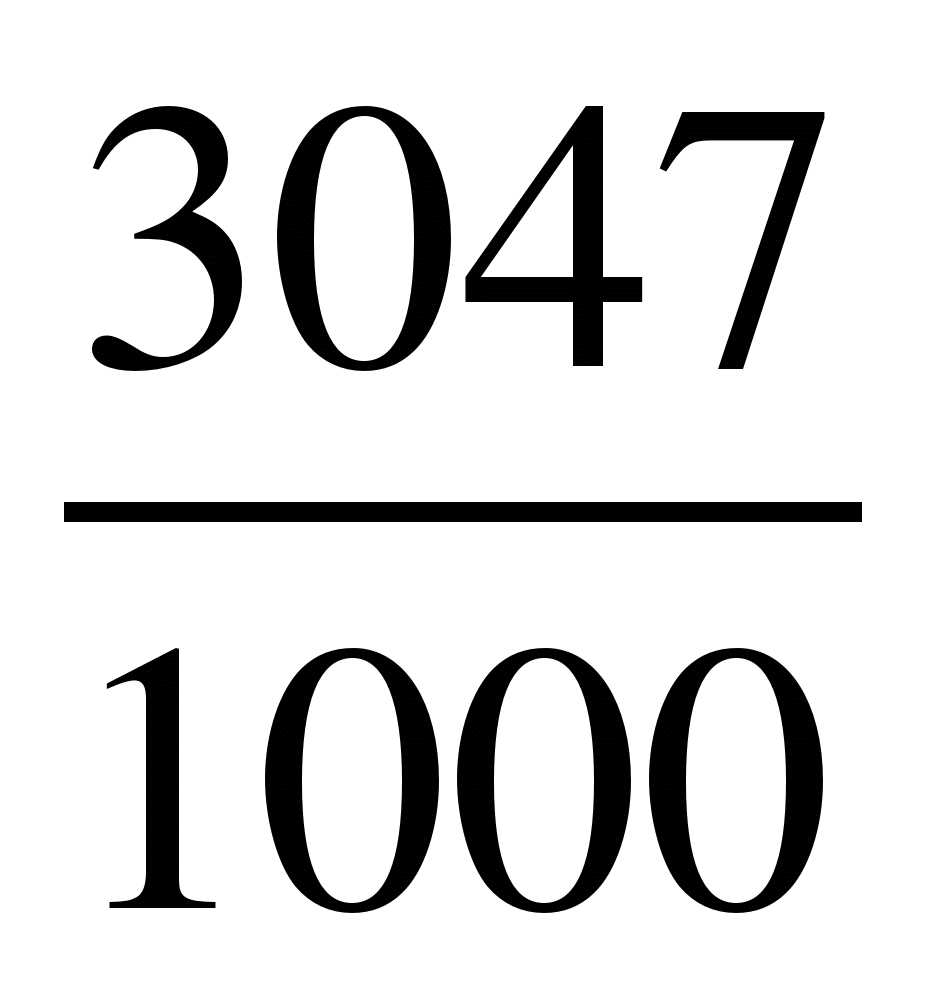 ; 6)
; 6)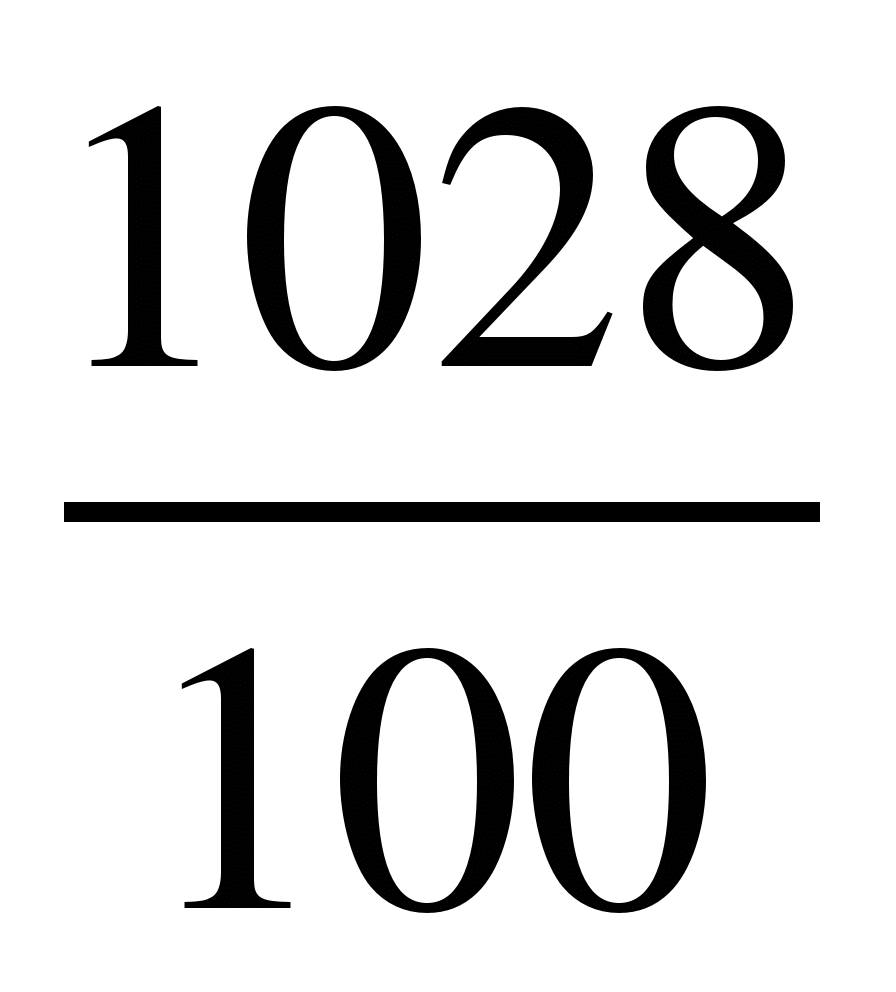 .
.
Представить в виде неправильной дроби:
7) 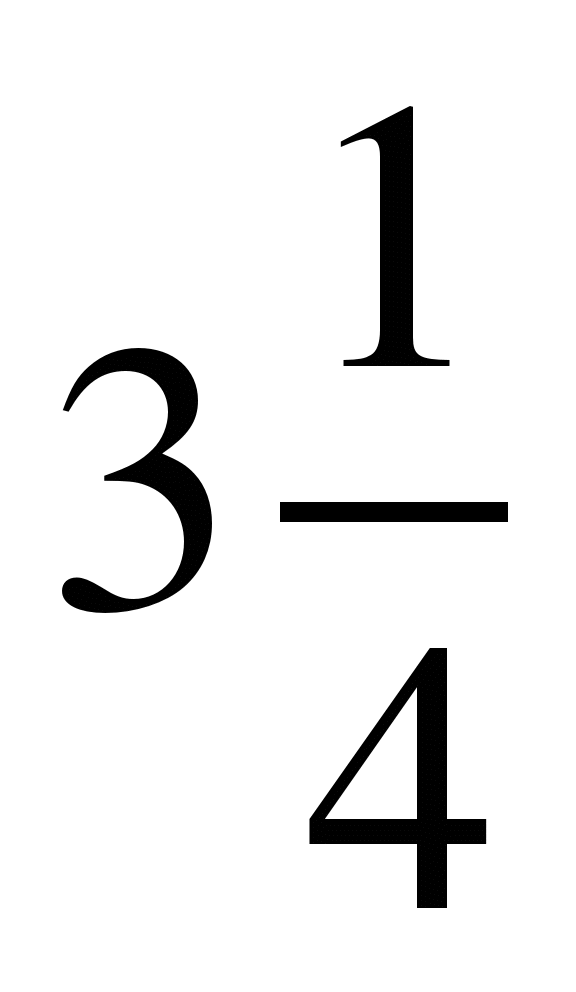 ; 8)
; 8) 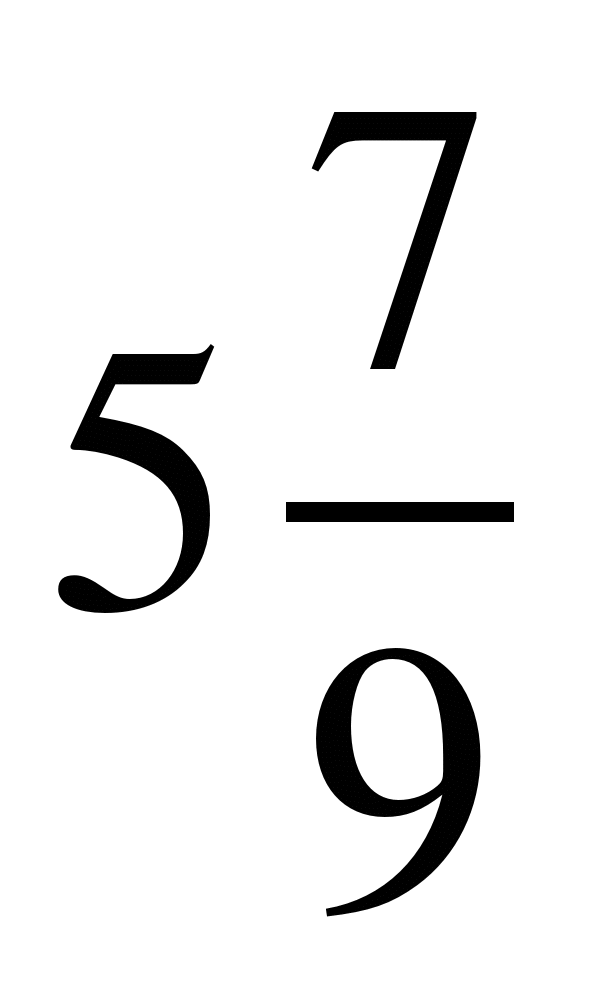 ;
;
9) 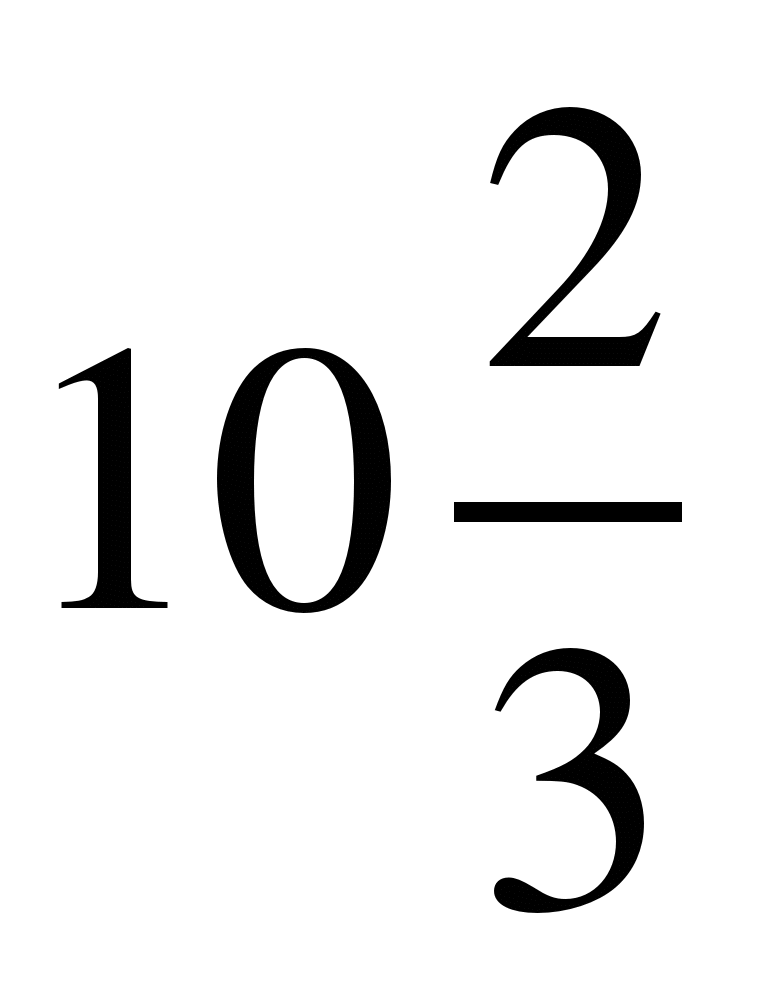 ; 10)
; 10)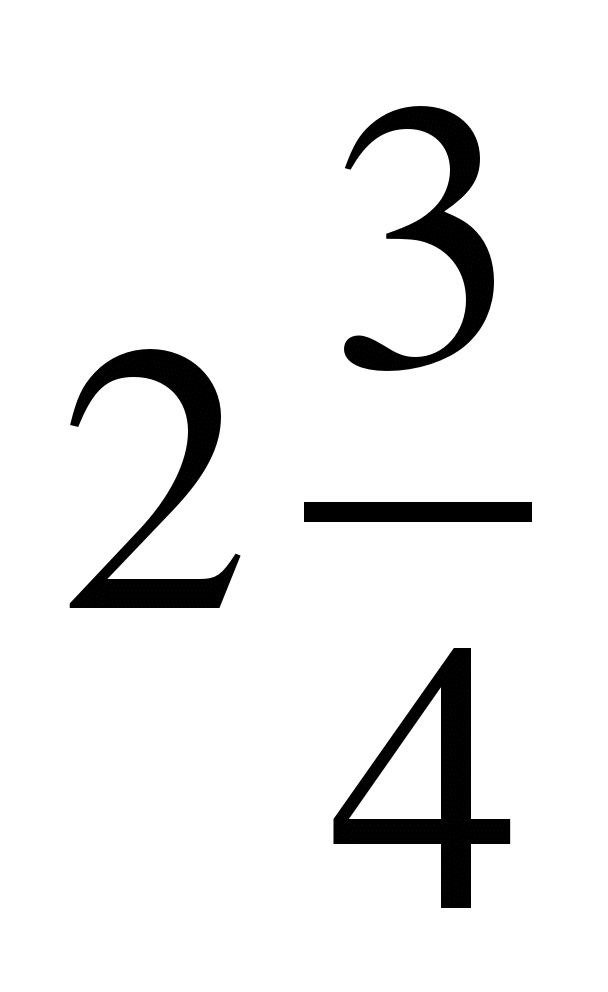 ; 11)
; 11)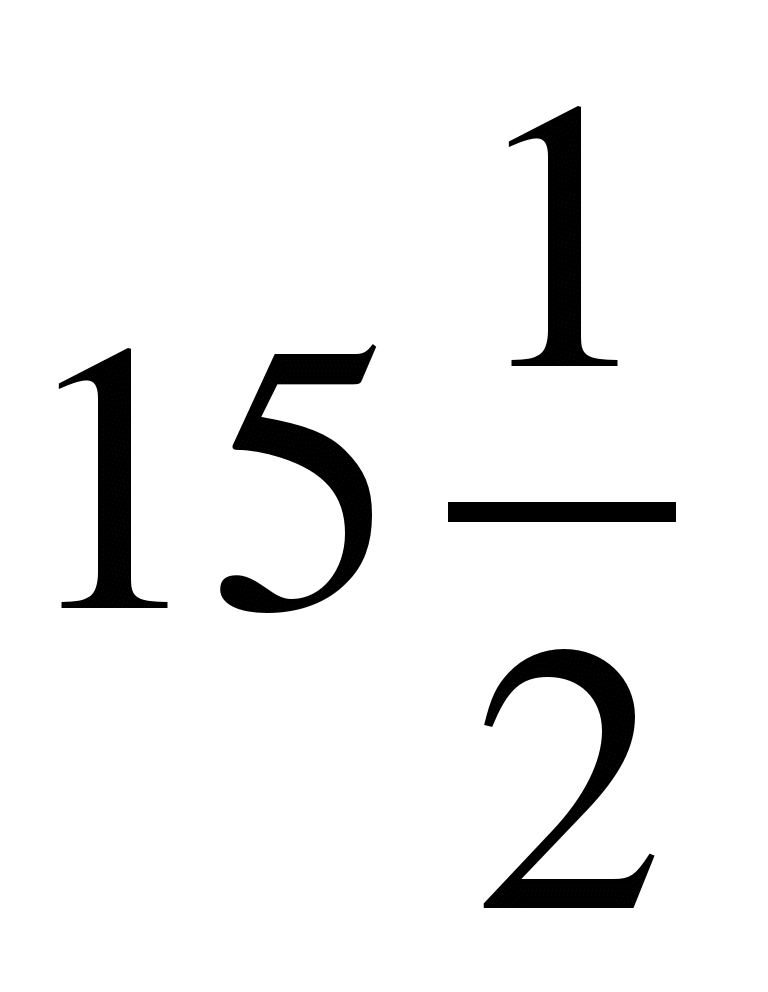 ; 12)
; 12) 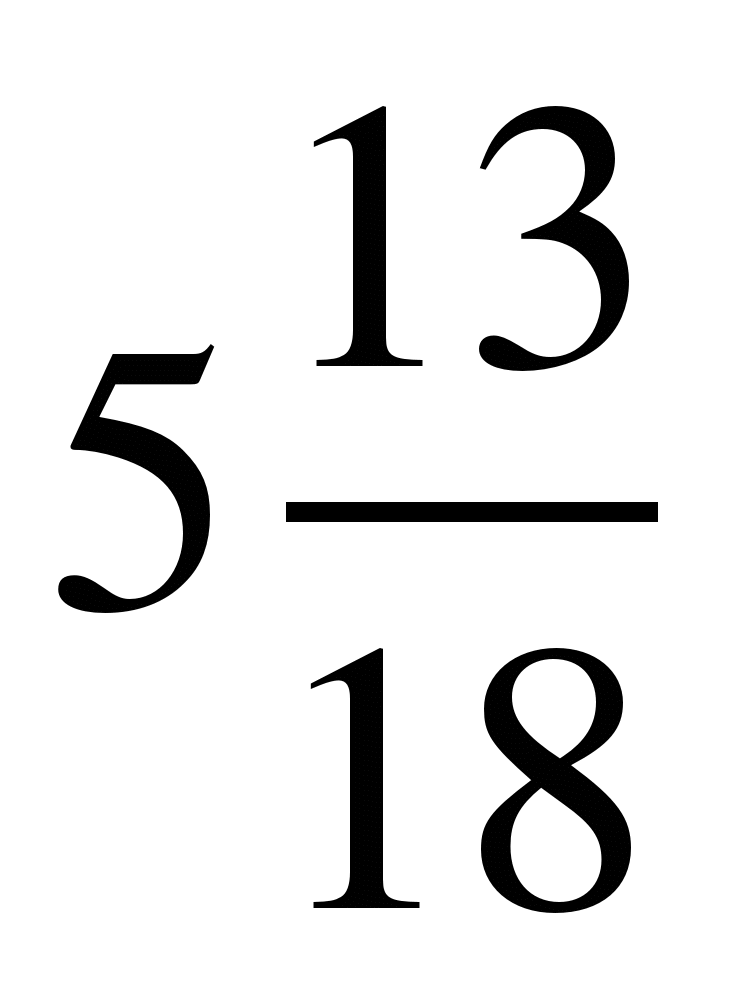 .
.
Сложение и вычитание смешанных чисел.
1) Сложить целые части;
2) Сложить дробные части;
3) Результаты сложить.
Чтобы вычесть смешанные числа, нужно:
1) Вычесть целые части;
2) Вычесть дробные части,
если числитель вычитаемого больше числителя уменьшаемого, то необходимо занять единицу от целой части уменьшаемого и выполнить вычитание;
3) Результаты сложить, если возможно сократить.
1) Выполните действие: 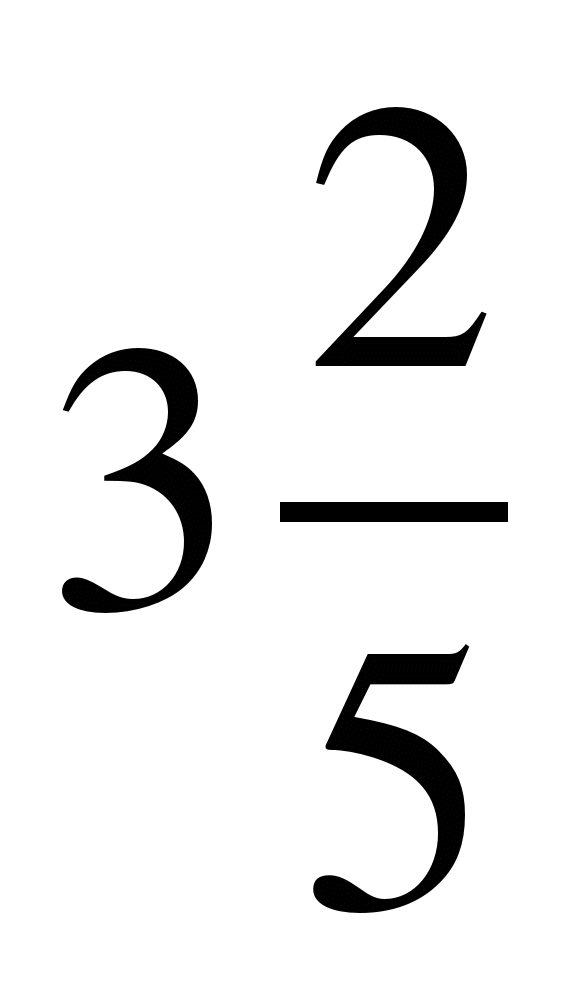 +
+ 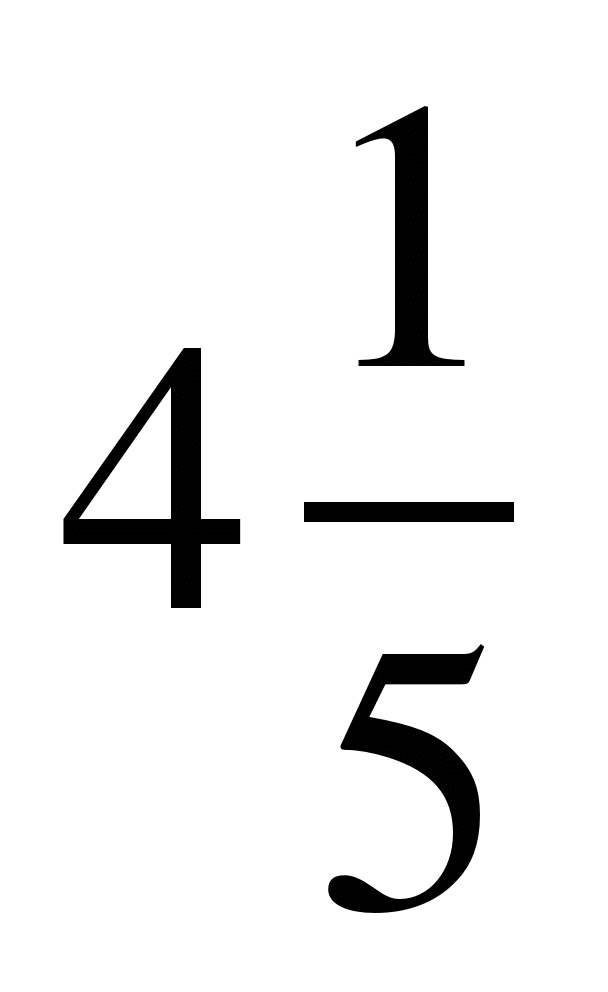 .
.
Решение:
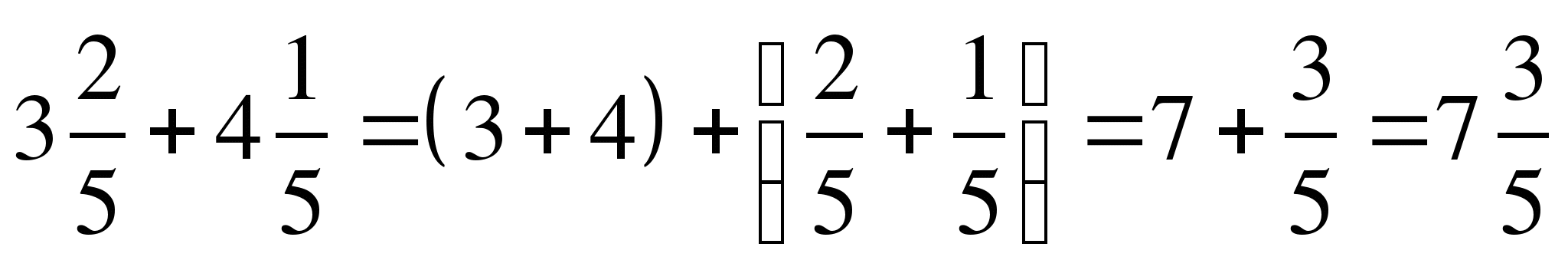
2) Выполните действие: а)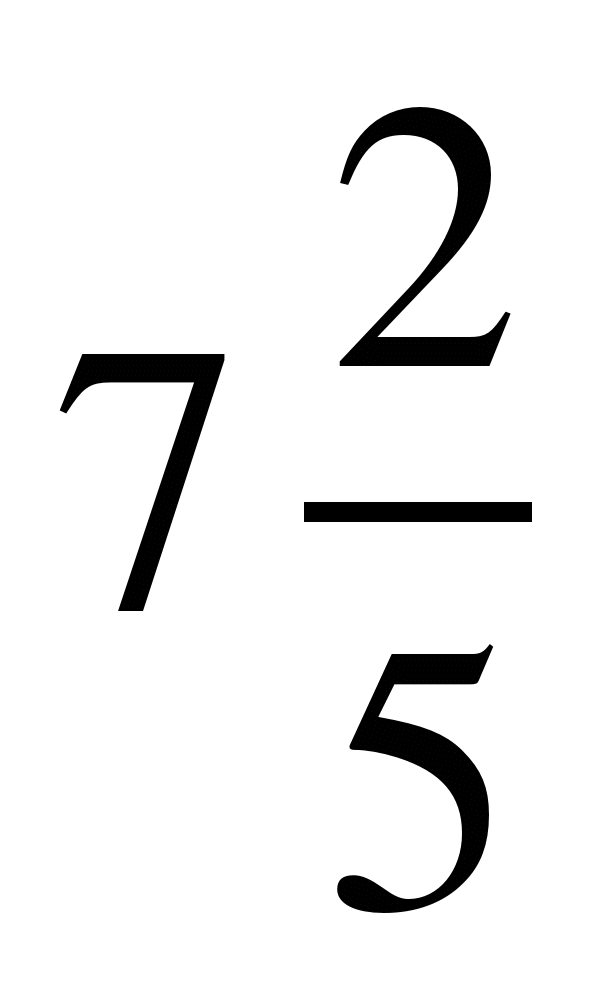 –
– 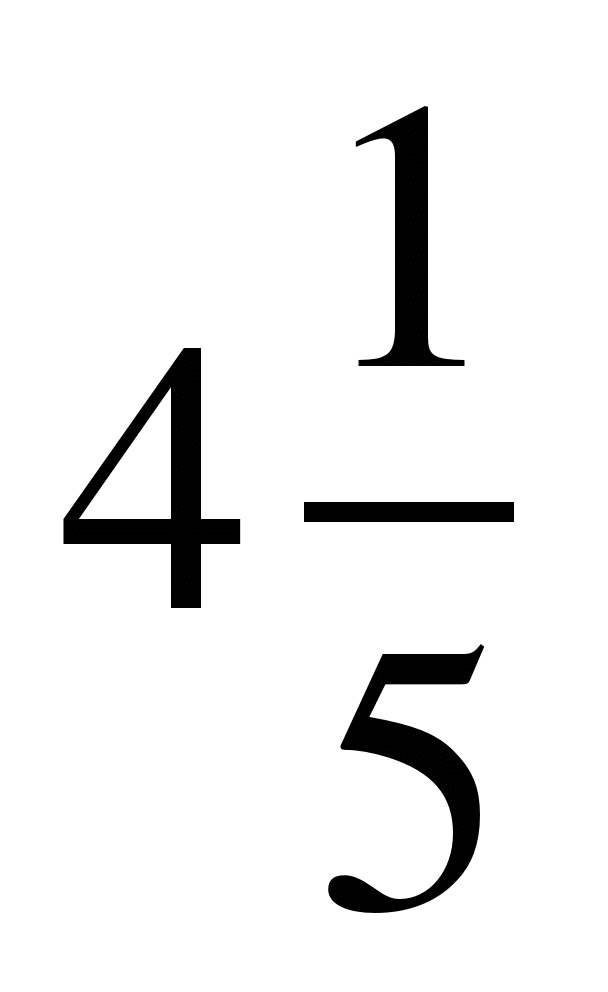 ;
;
б)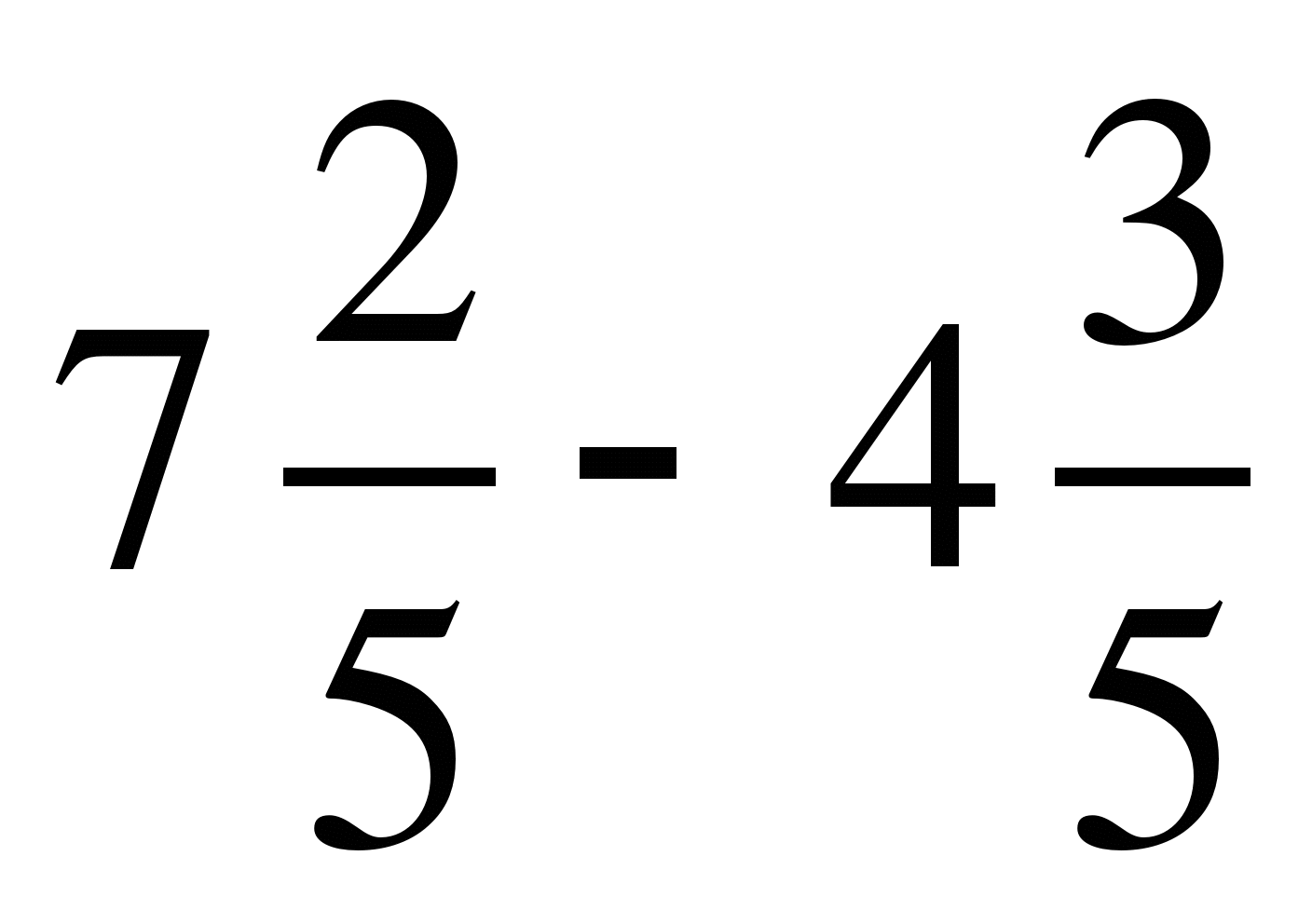 .
.
Решение:
а) 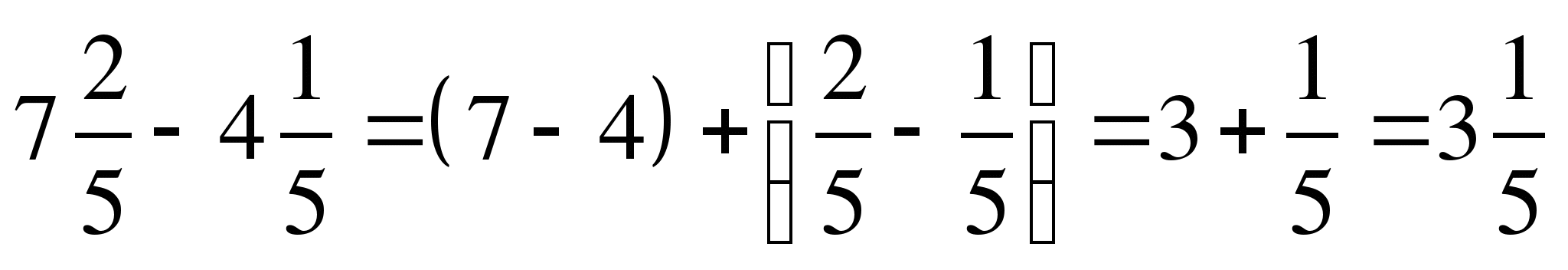
б)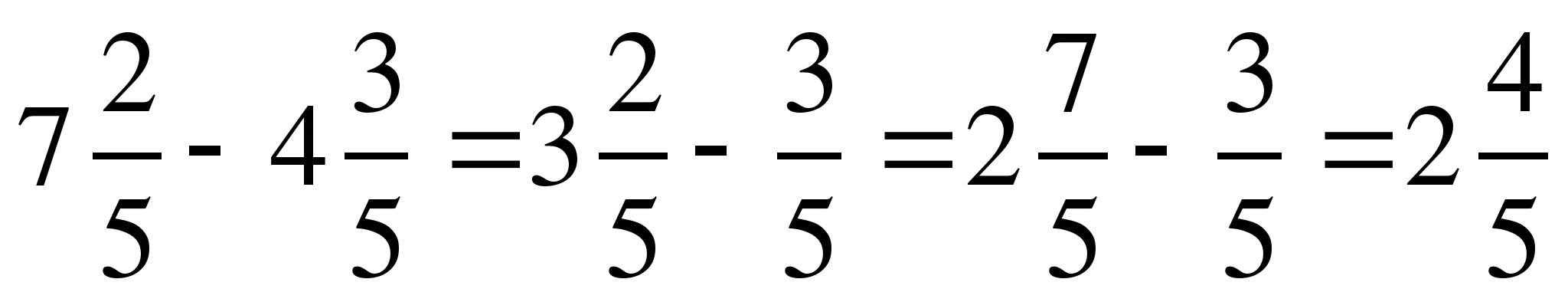
3) Вычисли: 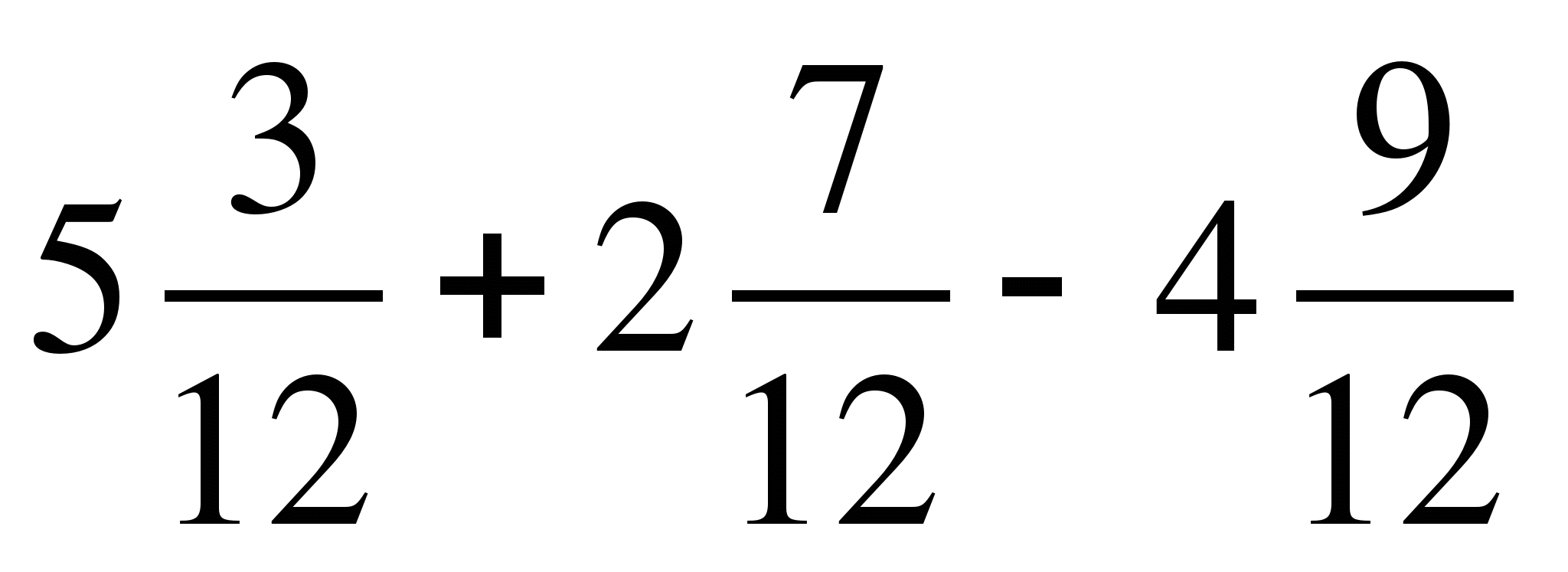 .
.
Решение:
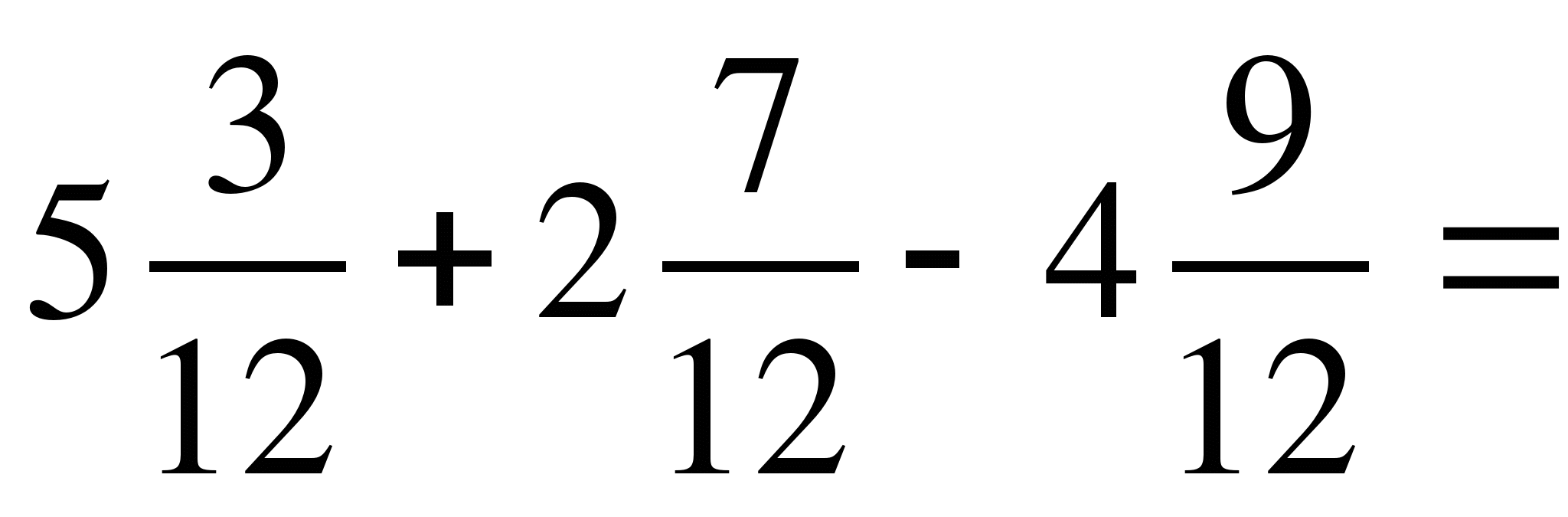
=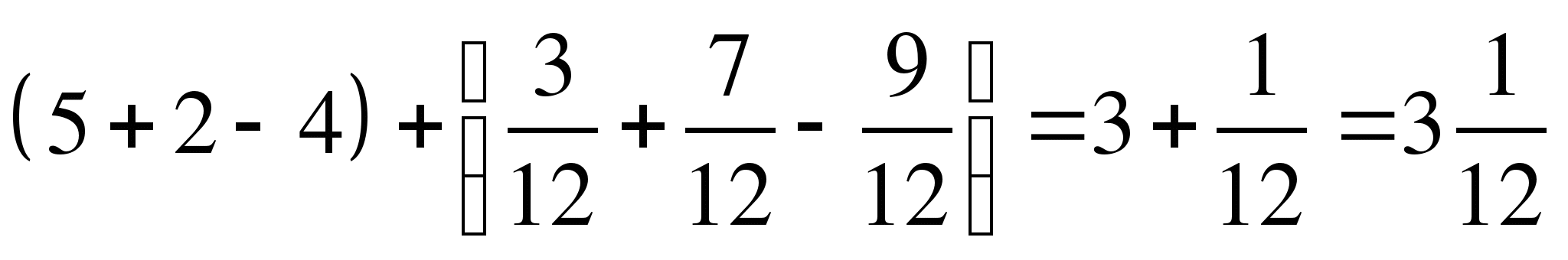
Вычисли:
1)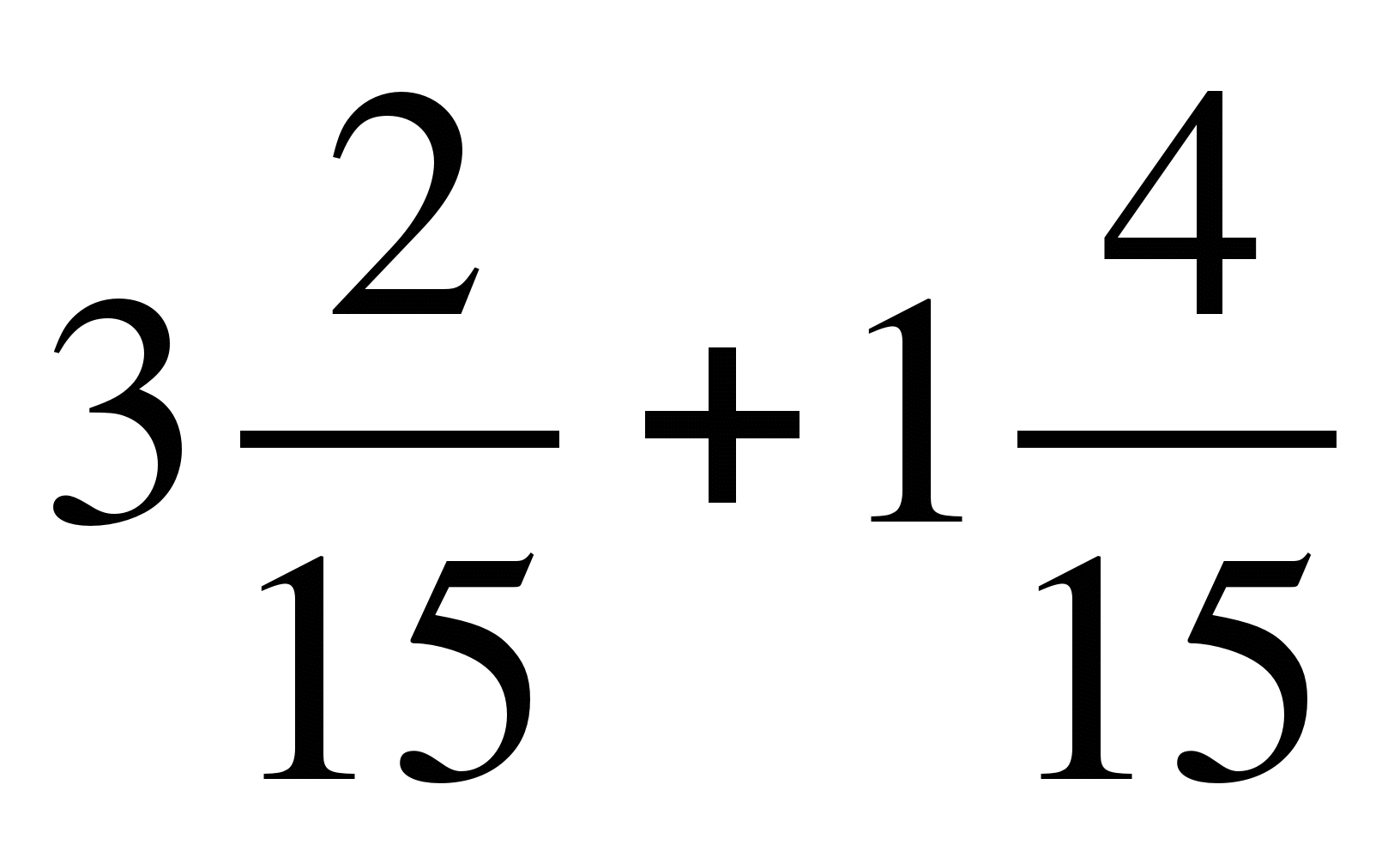 ;
;
2)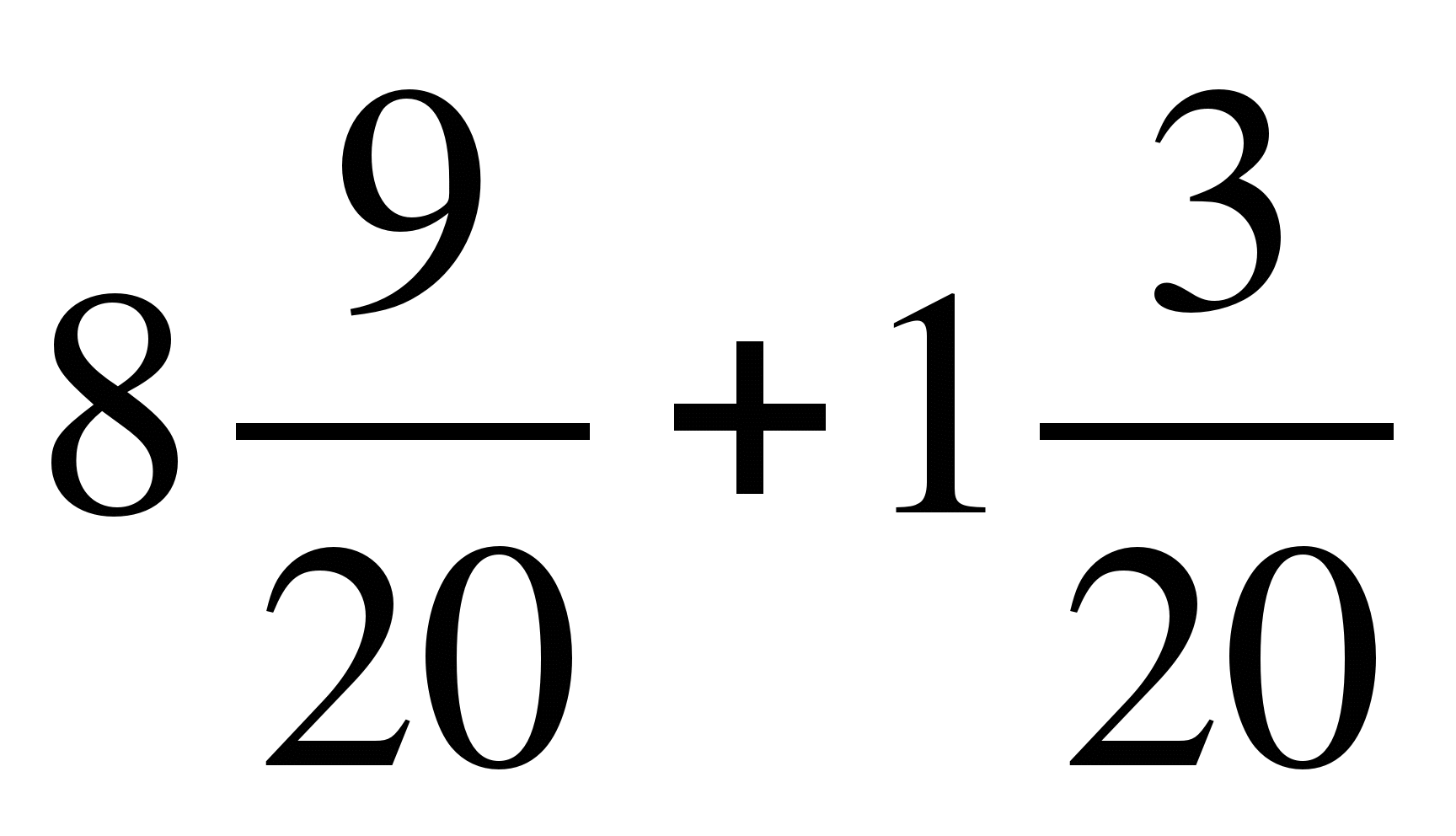 ;
;
3)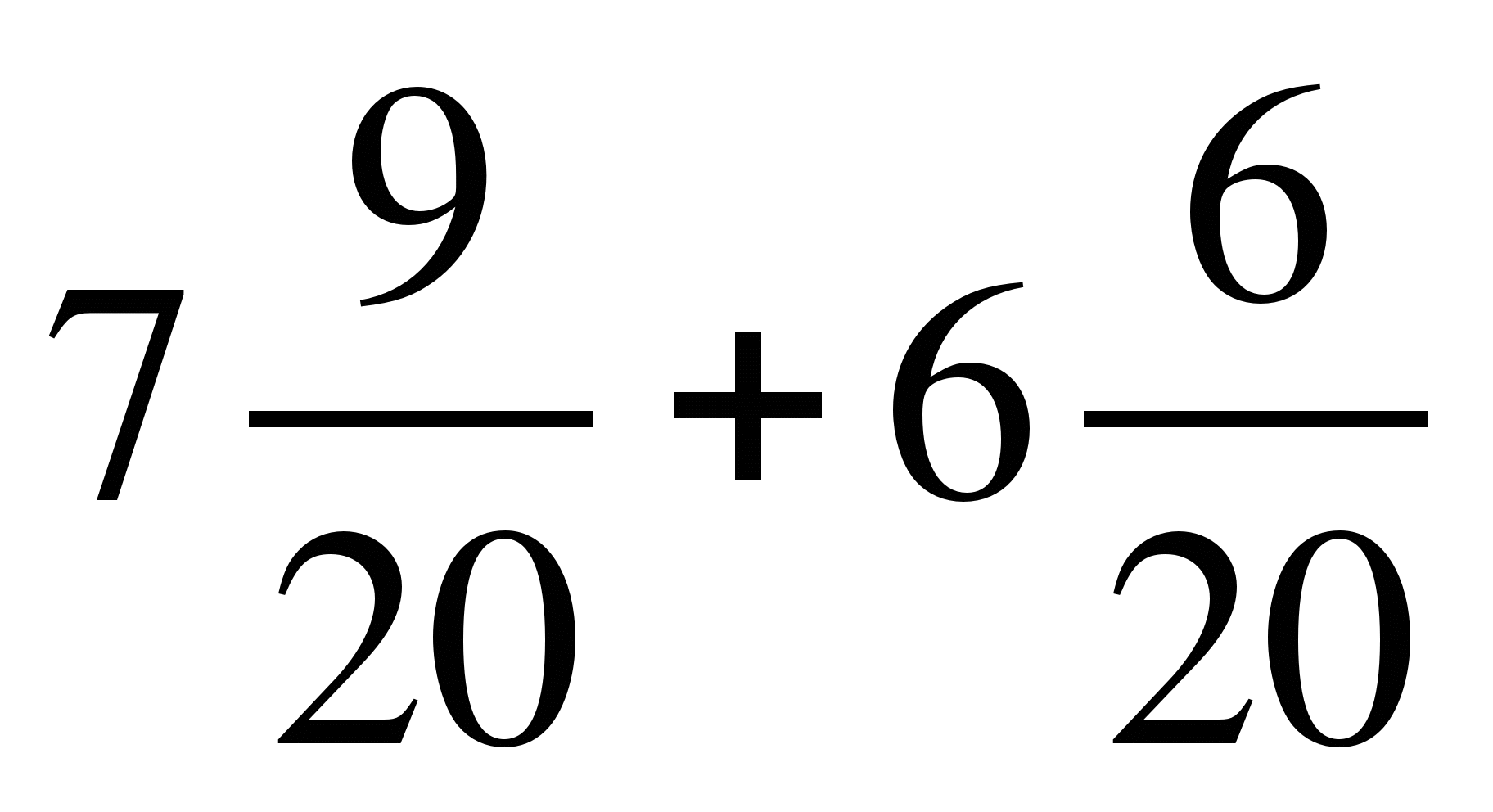 ;
;
4)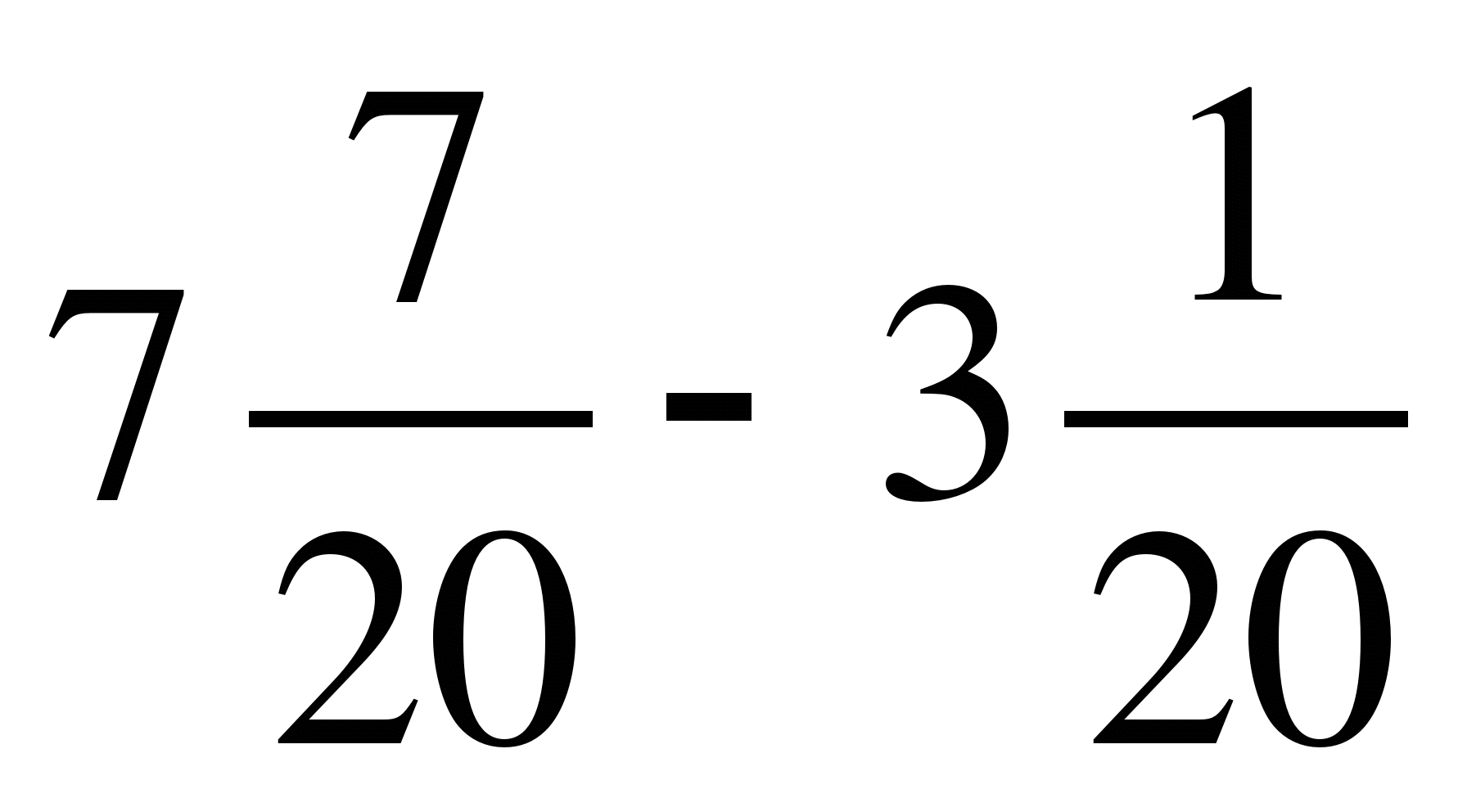 ;
;
5)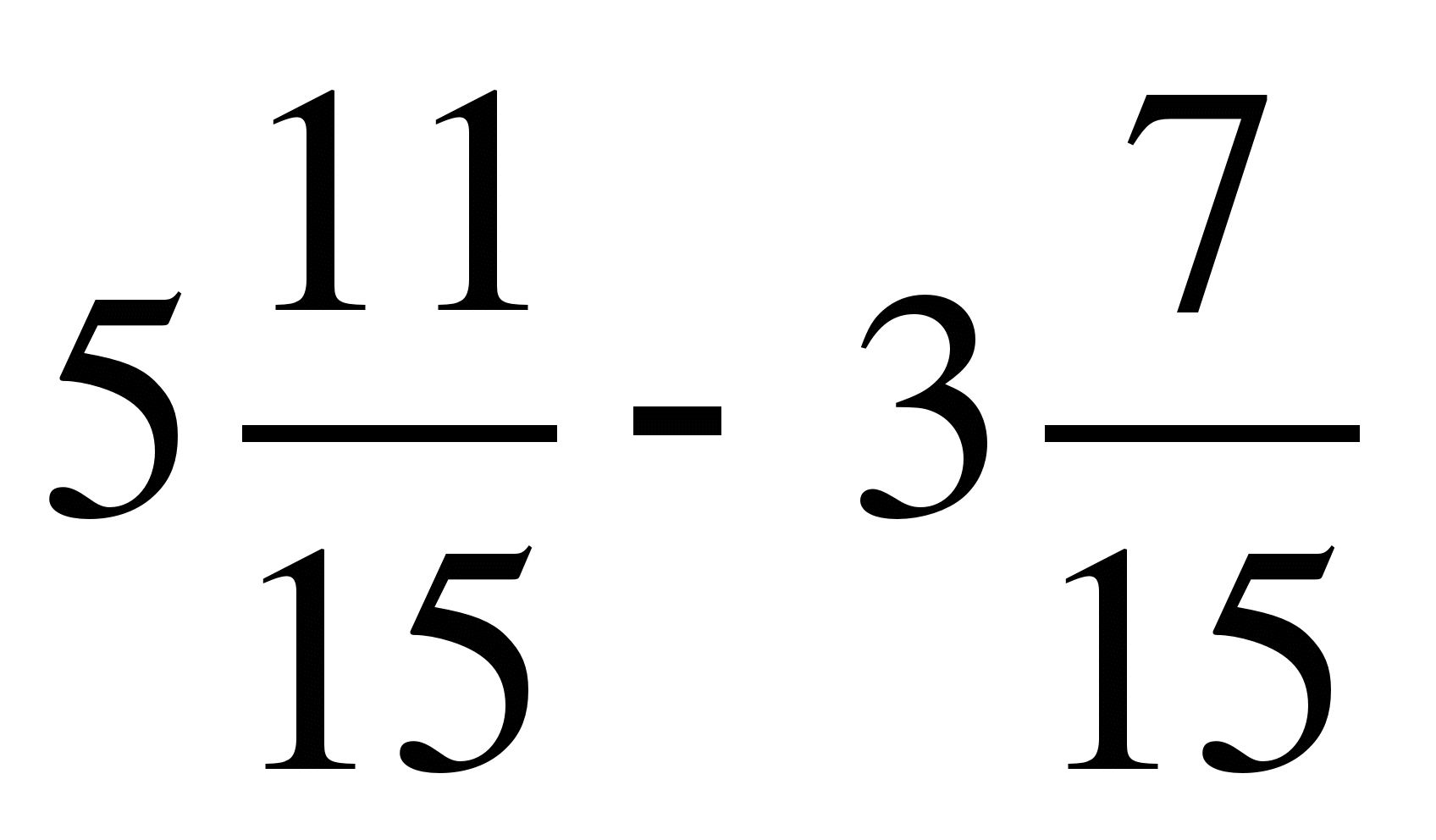 ;
;
6)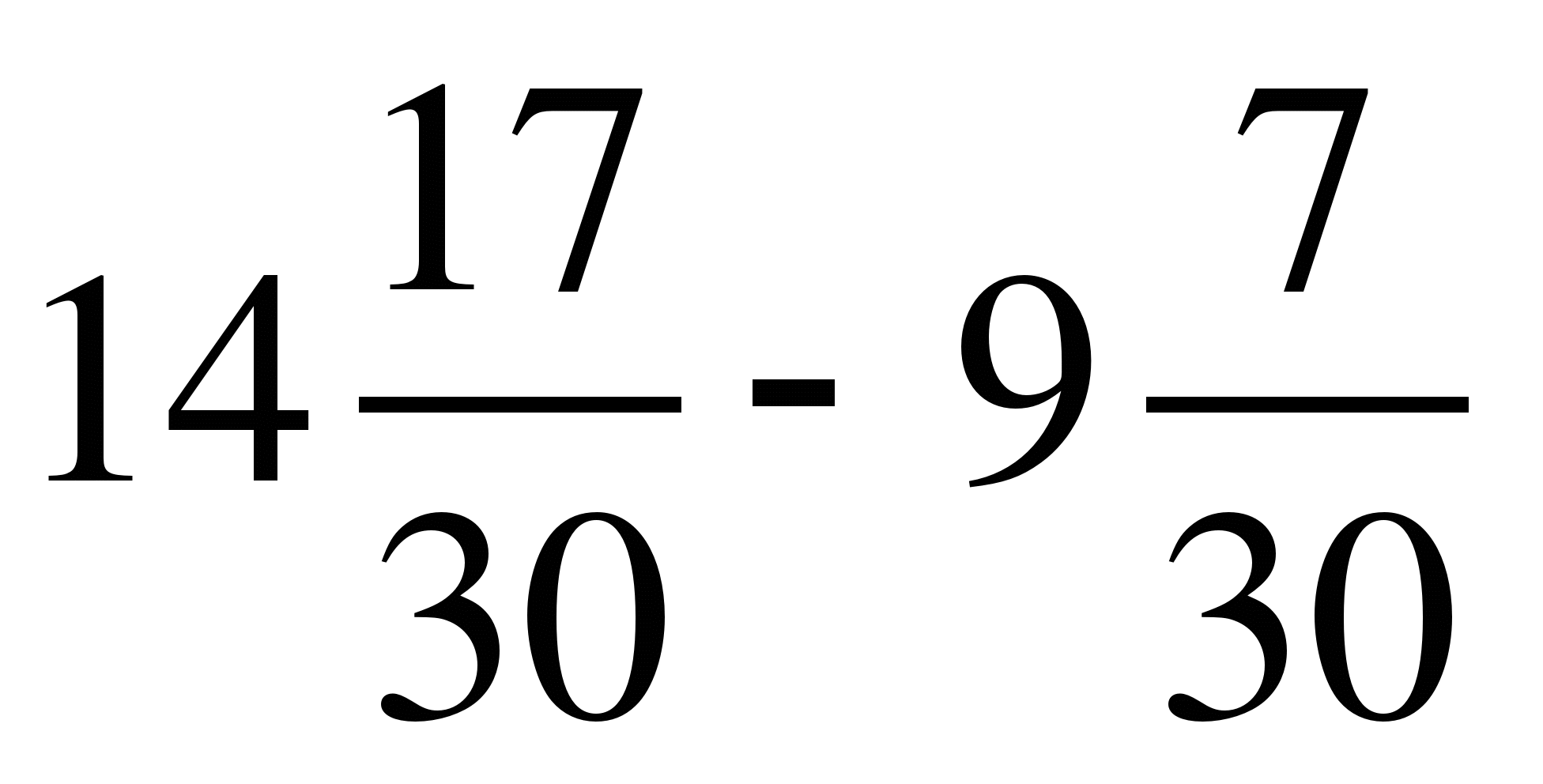 ;
;
7)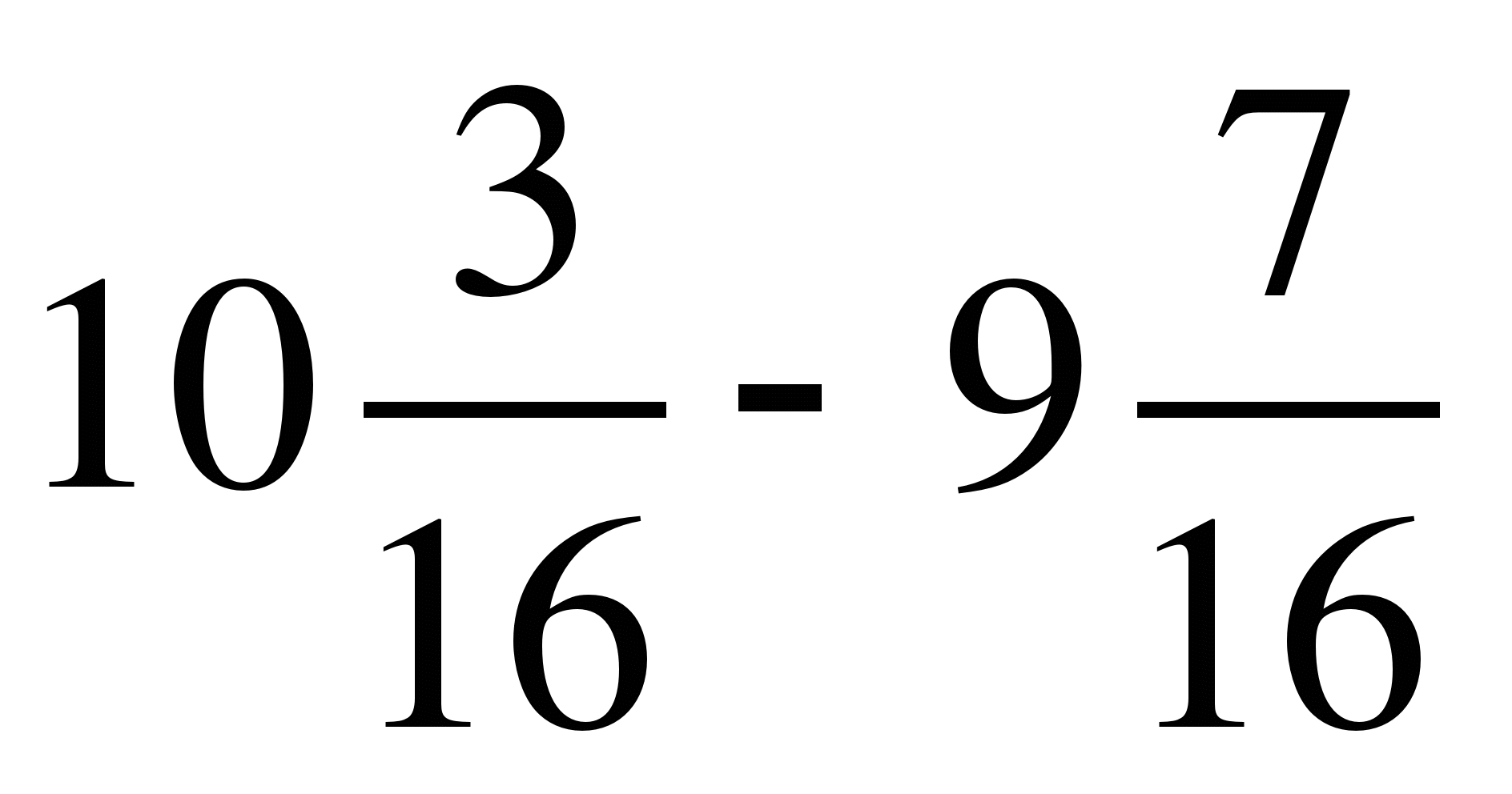 ;
;
8)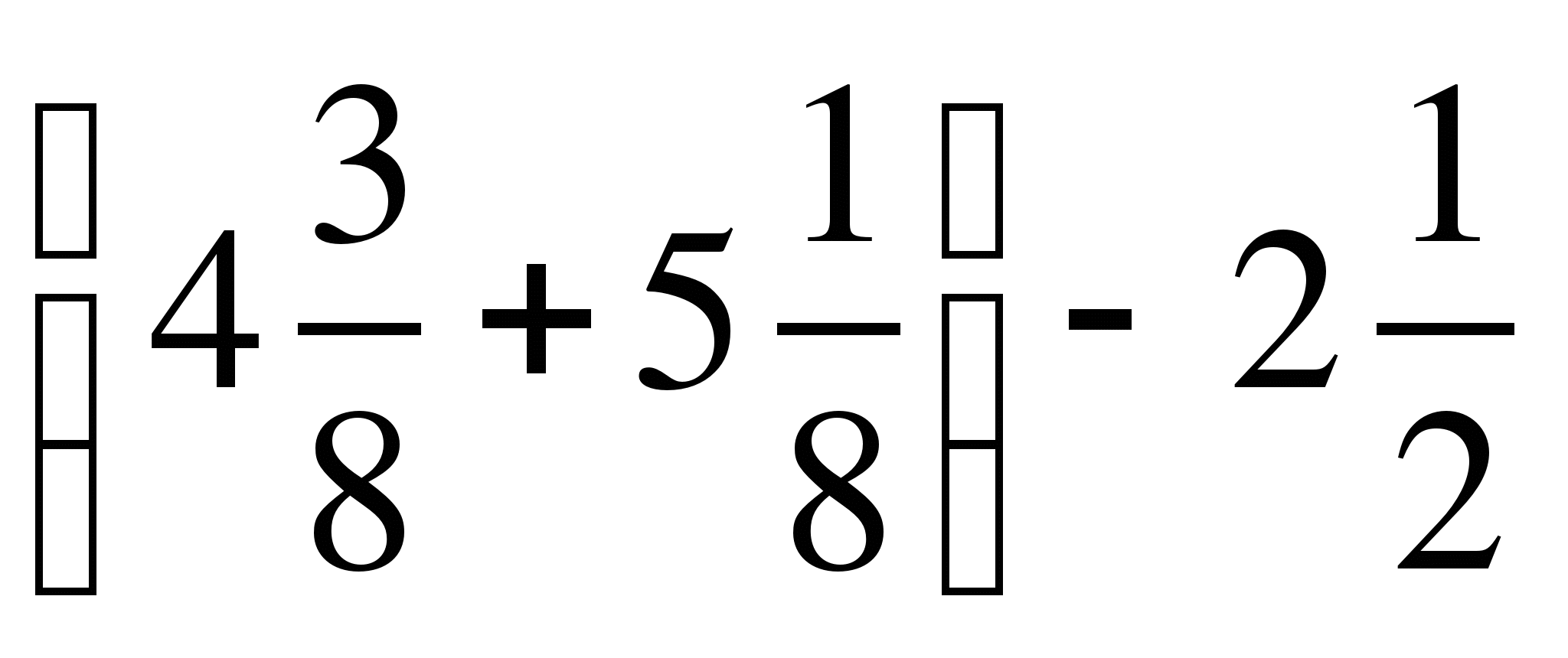 ;
;
9)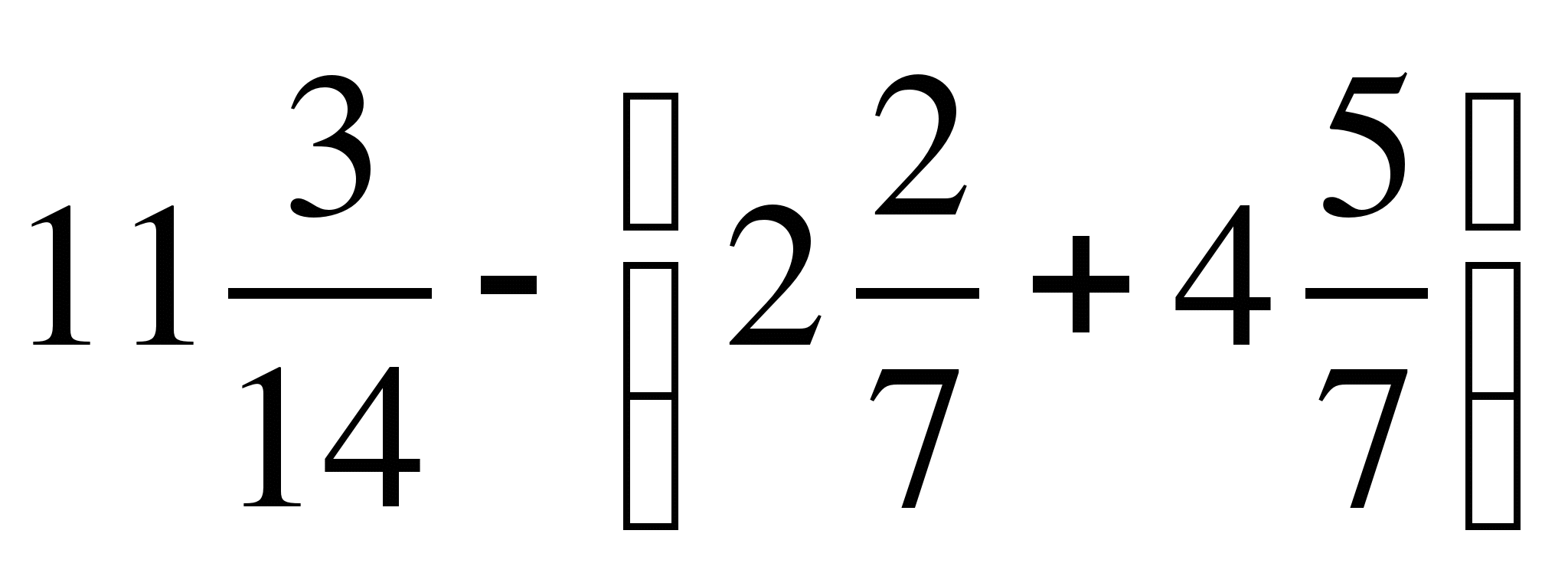 ;
;
10)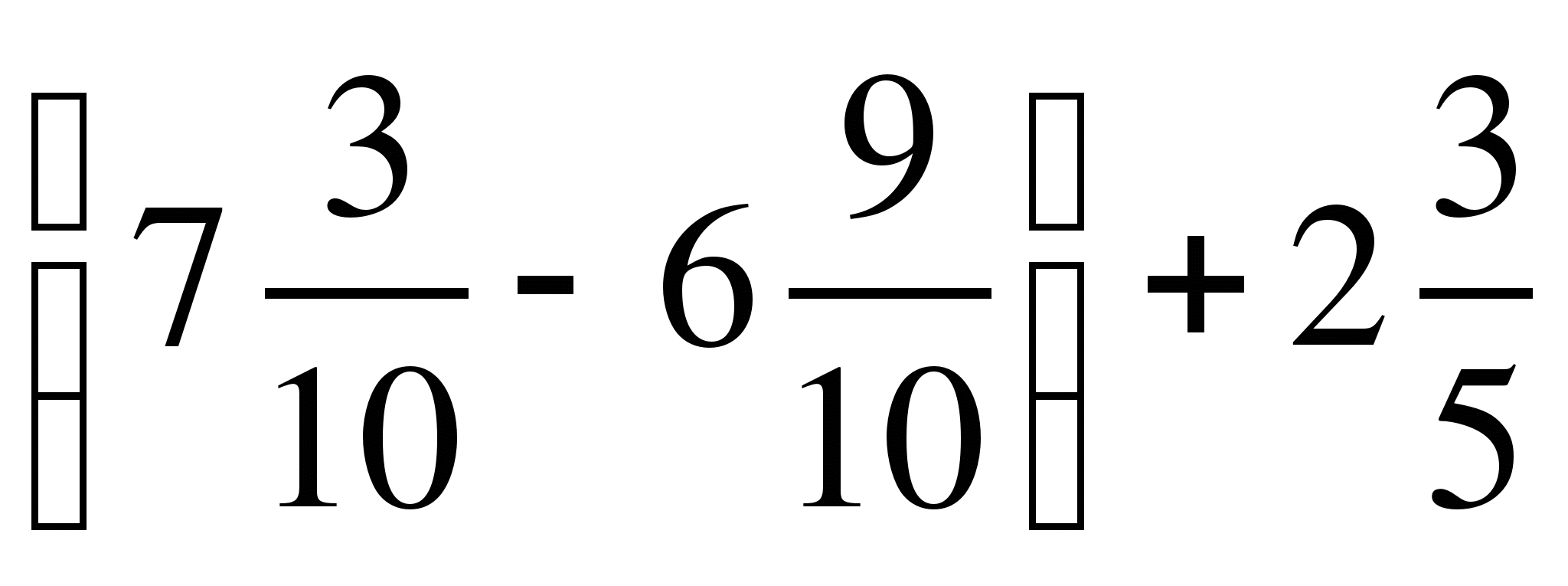 .
.
правильной, если знаменатель больше числителя.
Дробь называется неправильной, если знаменатель меньше числителя.
Чтобы неправильную дробь представить в виде смешанного числа, нужно числитель разделить на знаменатель.
Чтобы смешанное число представить в виде неправильной дроби нужно:

Образец
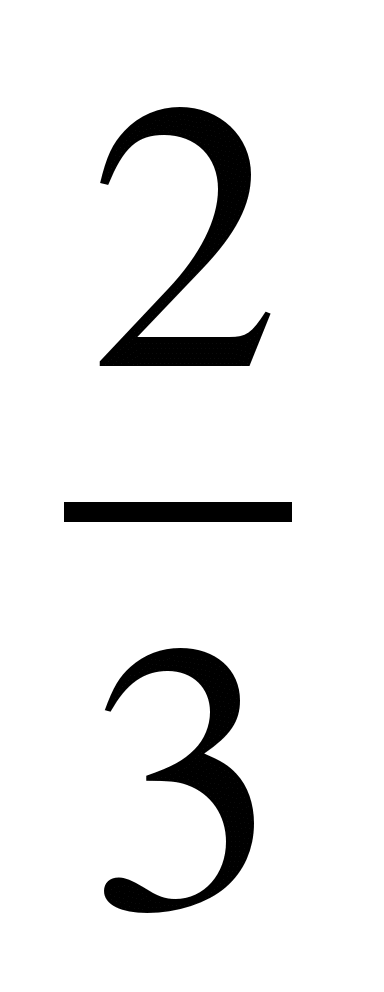 – правильная дробь.
– правильная дробь.
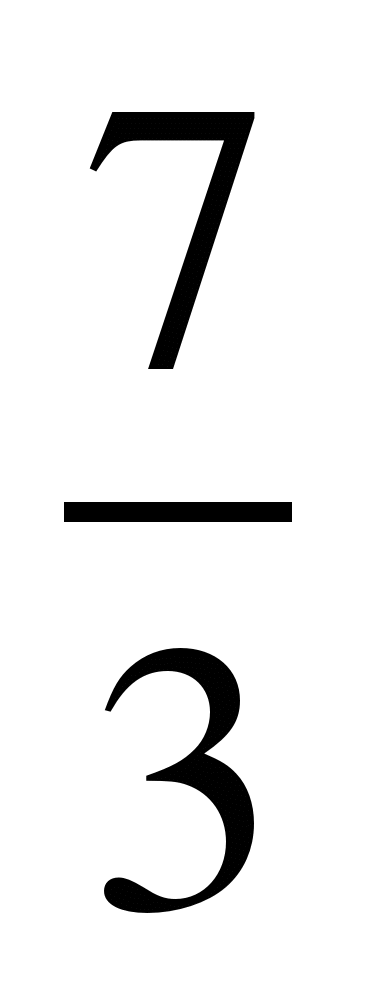 – неправильная дробь.
– неправильная дробь.
1) Выделить целую часть из дроби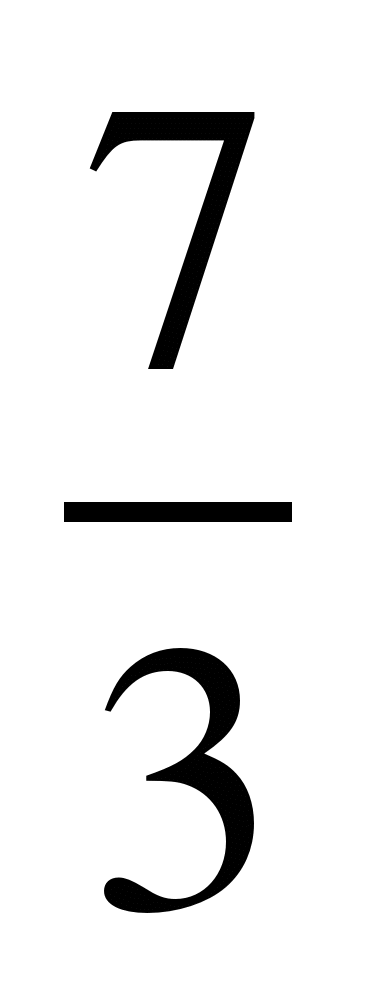 , это значит числитель 7 разделить на знаменатель 3.
, это значит числитель 7 разделить на знаменатель 3.
Решение:
1 – остаток от деления = числитель
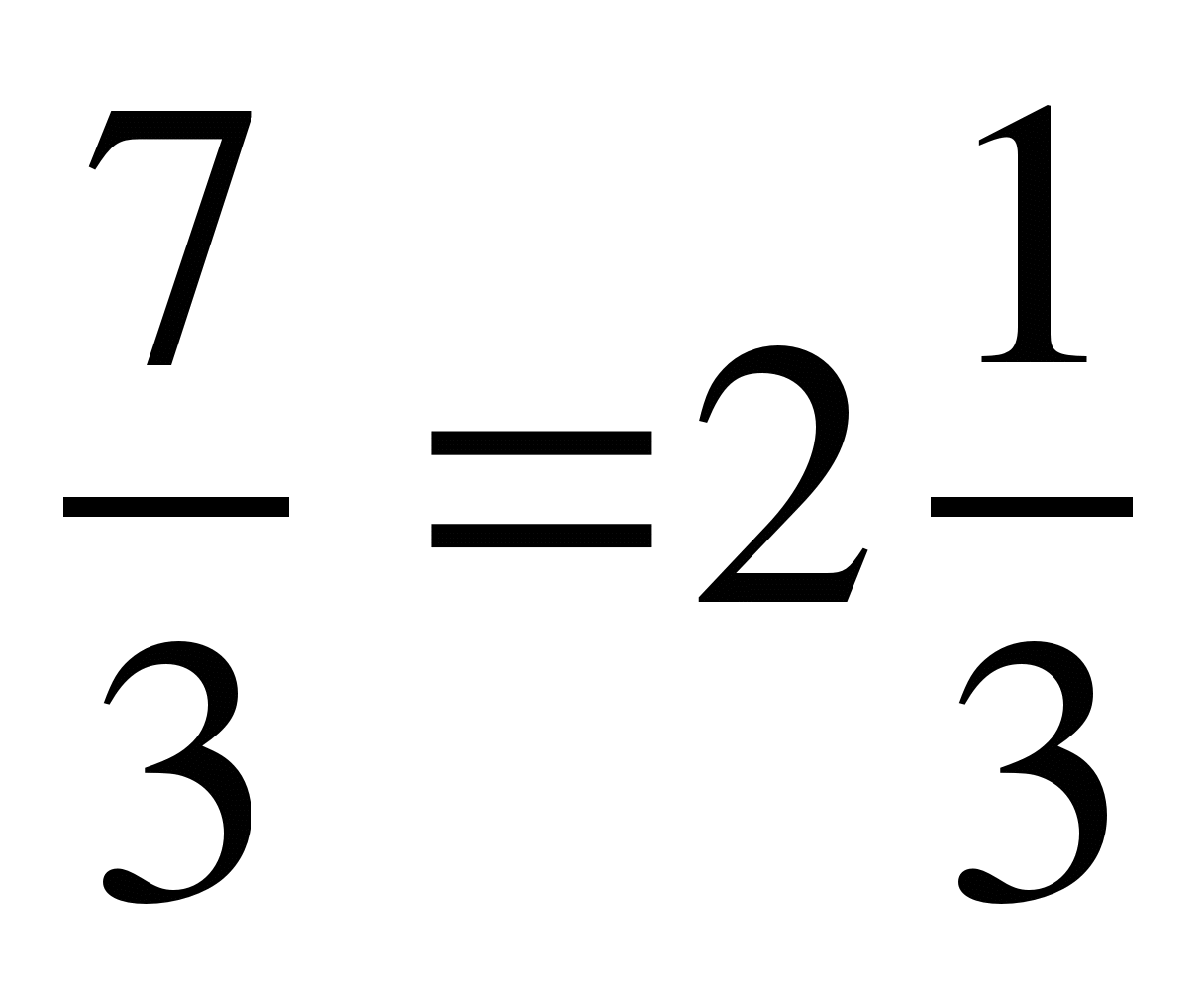
2) Записать число 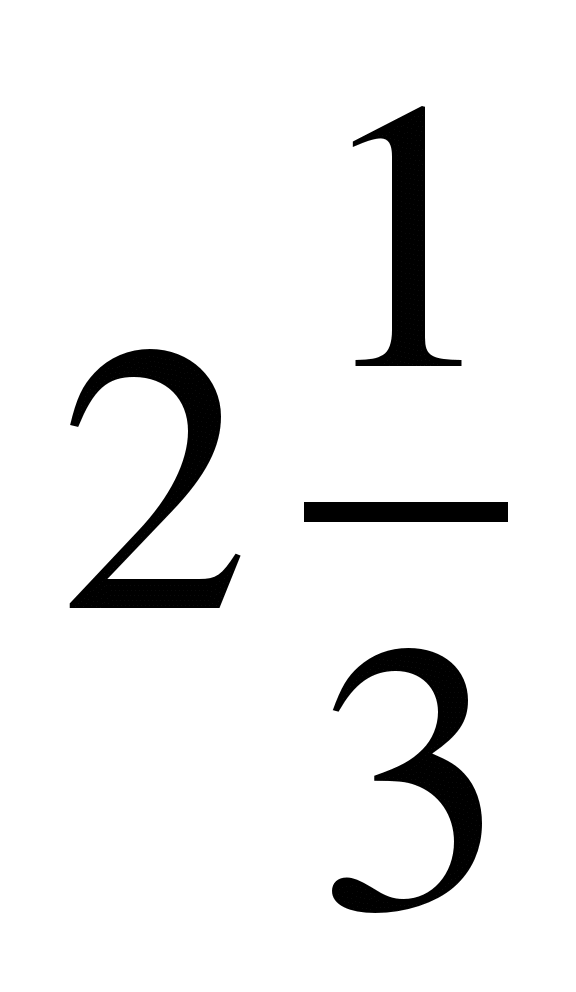 в виде неправильной дроби.
в виде неправильной дроби.
Решение:
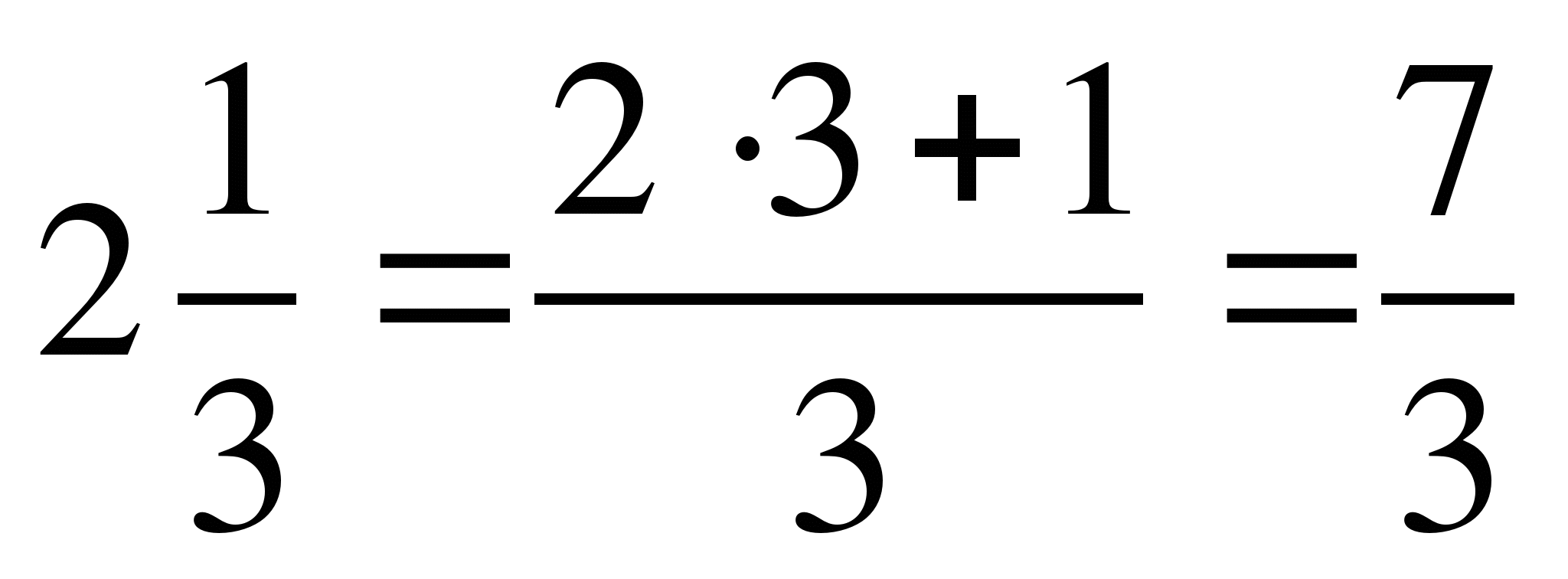
Умножение и деление смешанных чисел
Чтобы умножить смешанные числа, нужно:
Смешанное число представить в виде неправильной дроби
Выполнить умножение обыкновенных дробей.
Если в результате получили неправильную дробь, представьте ее в виде смешанного числа
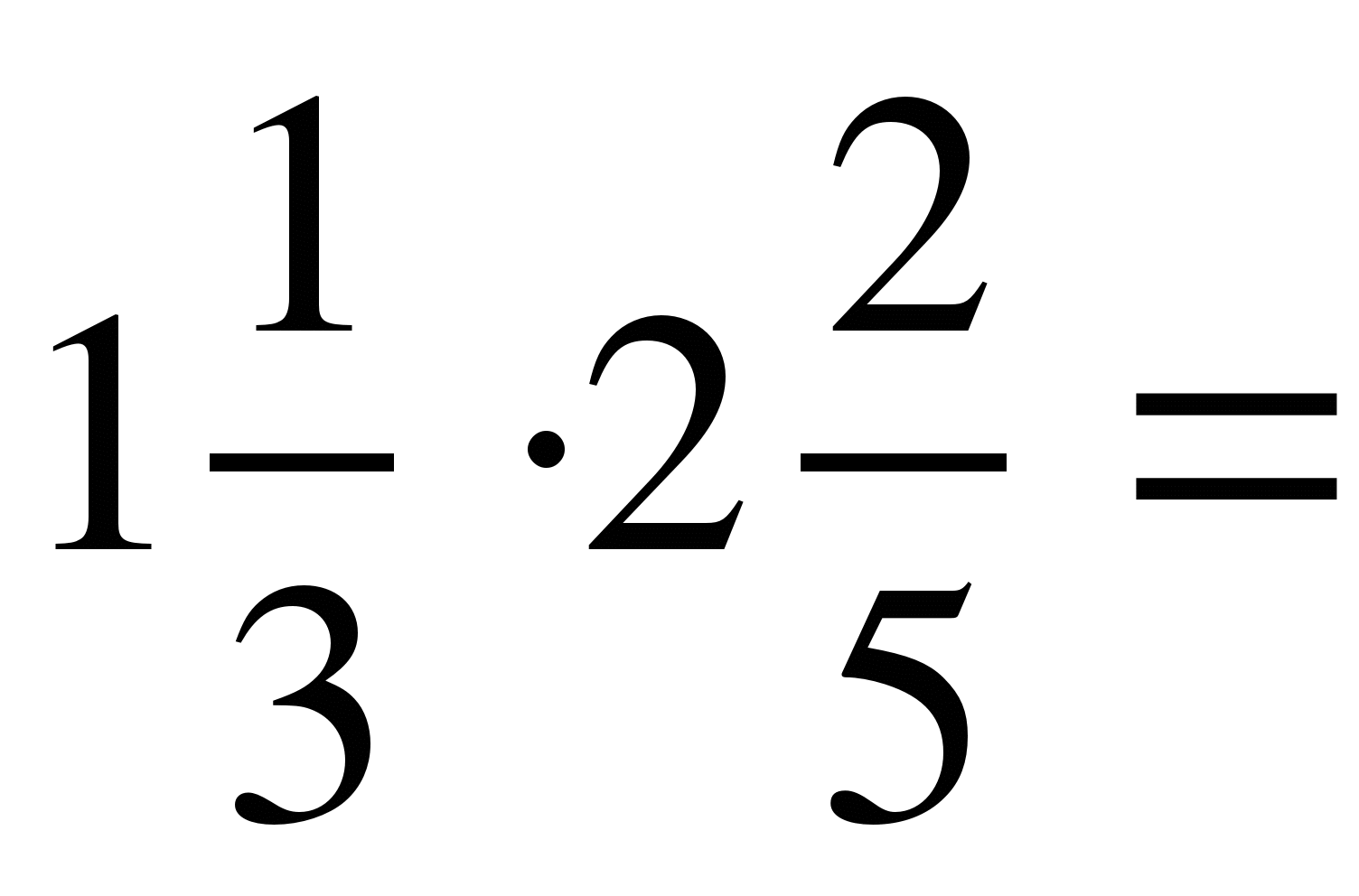
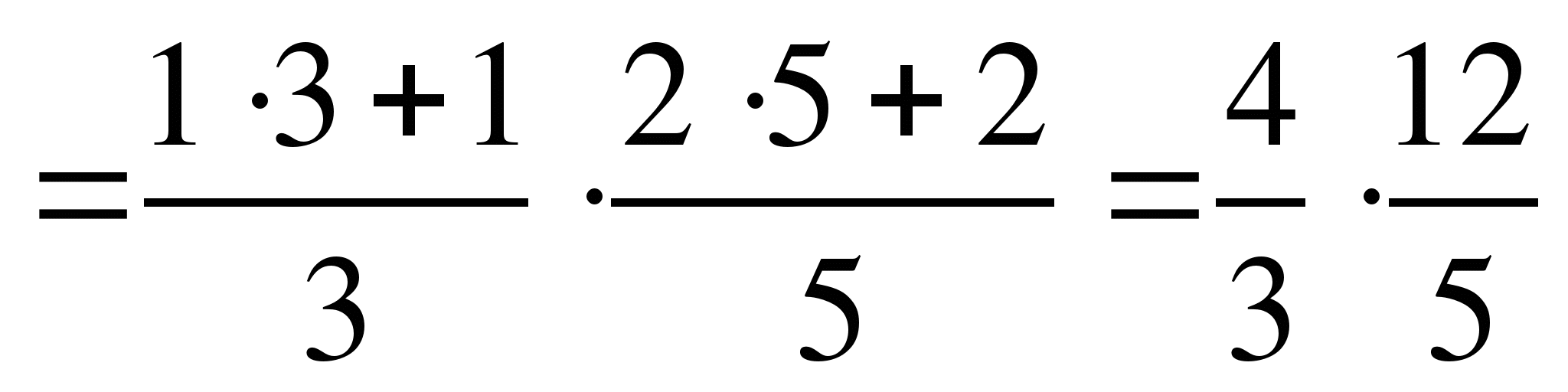
=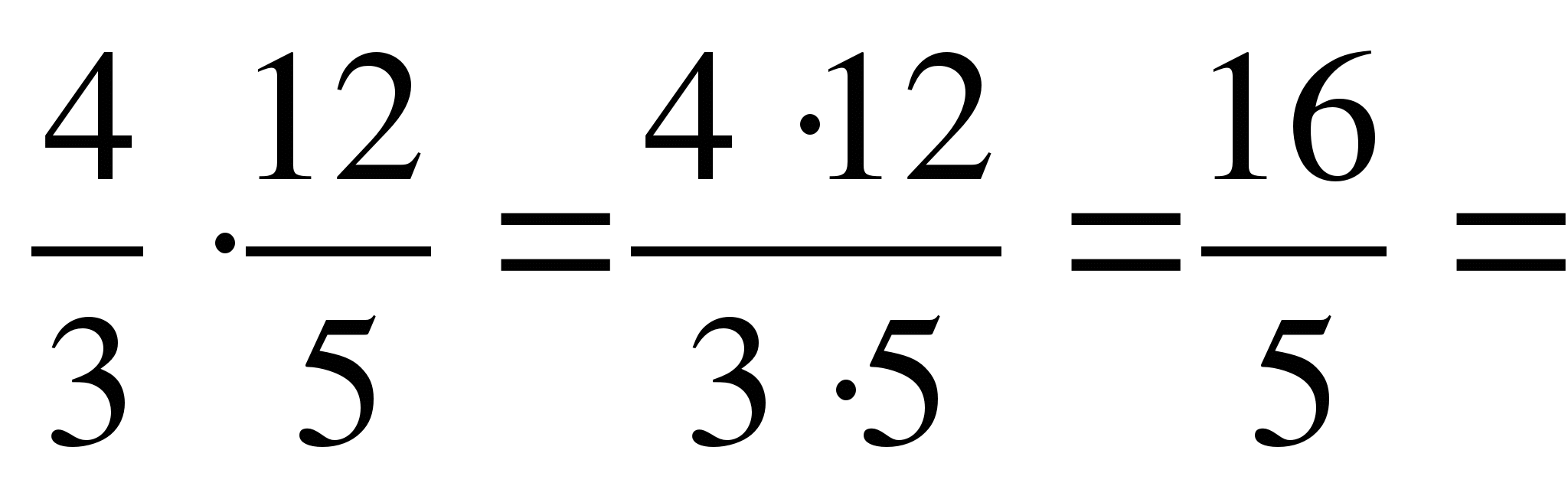
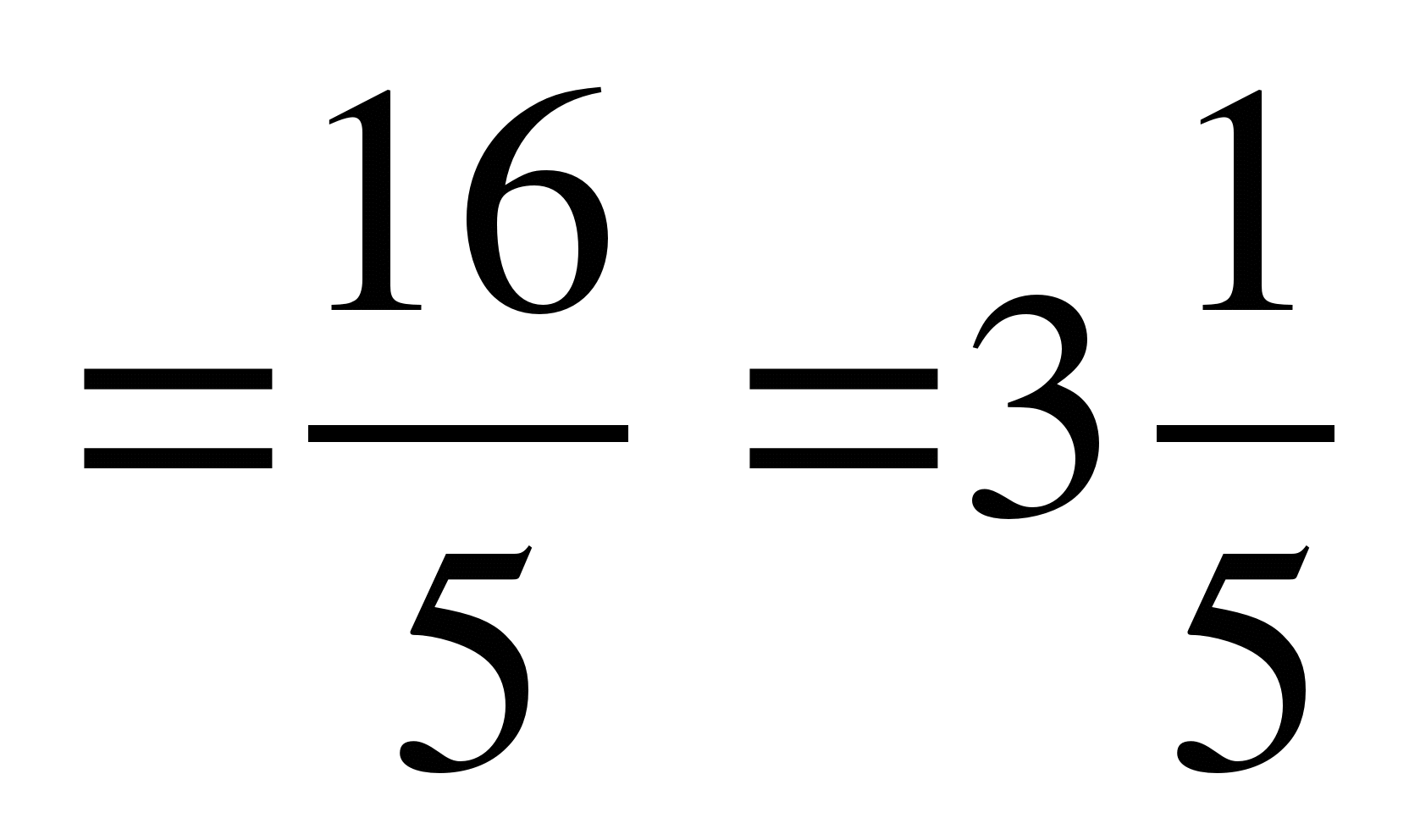
Чтобы разделить смешанные числа, нужно:
Смешанное число представить в виде неправильной дроби
Выполнить деление обыкновенных дробей.
Если в результате получили неправильную дробь, представьте ее в виде смешанного числа
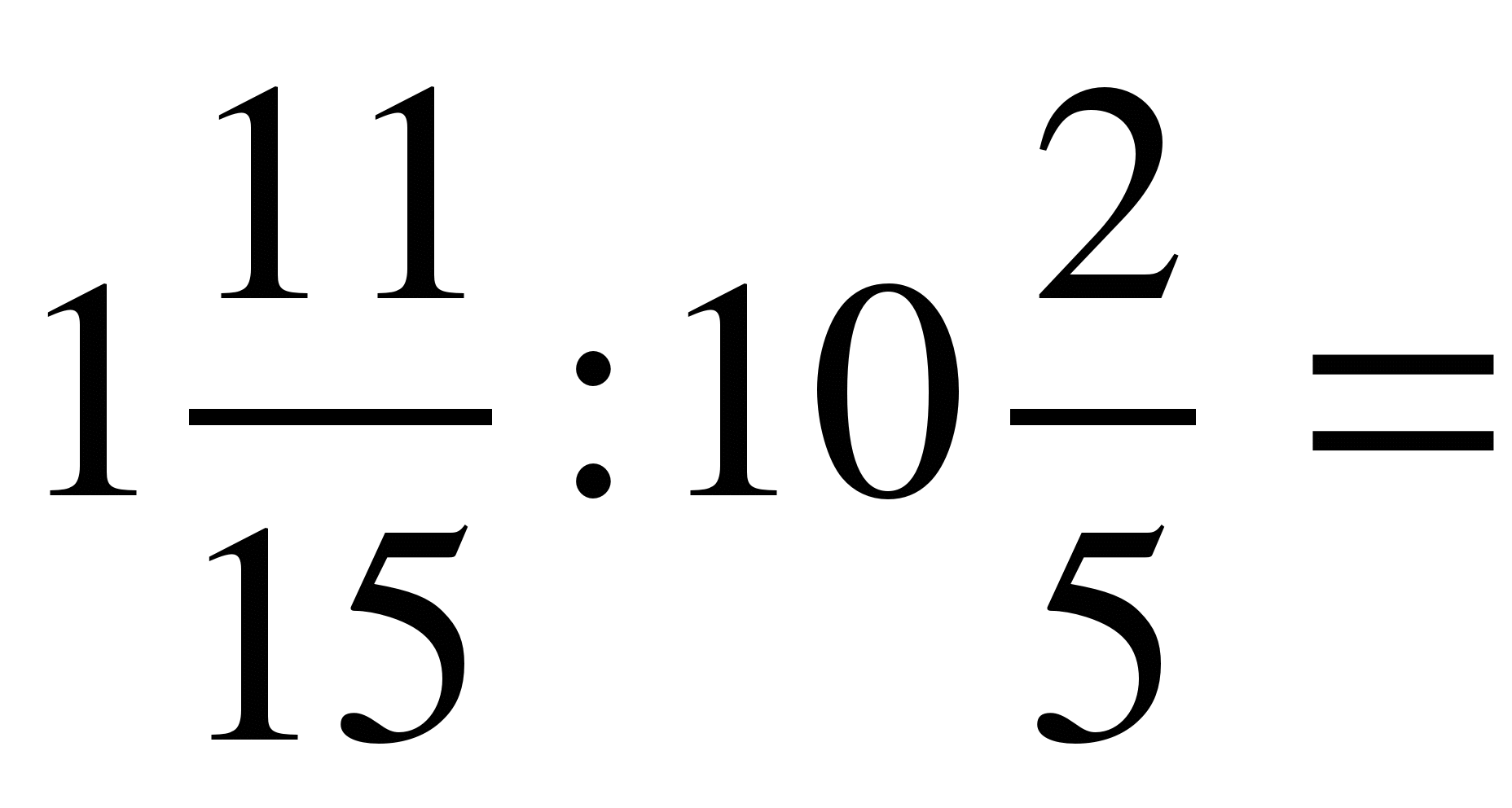
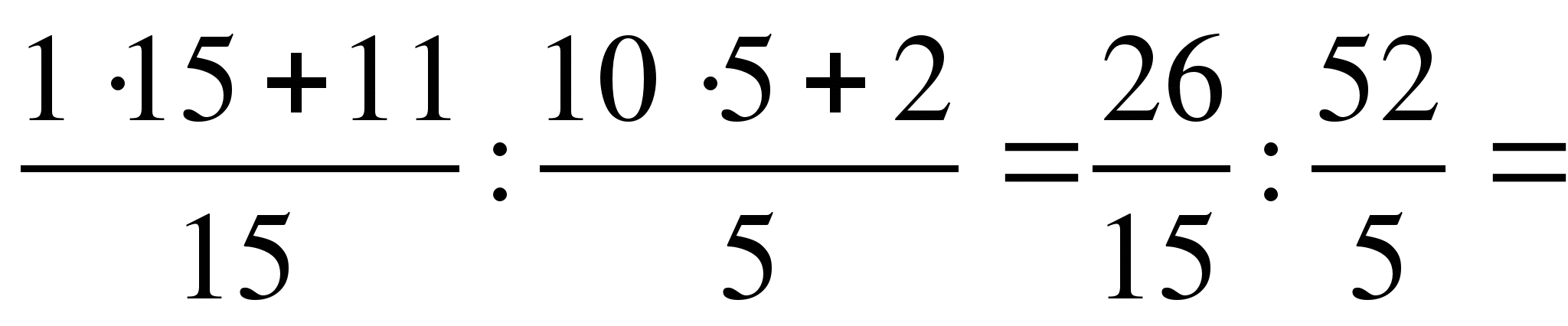
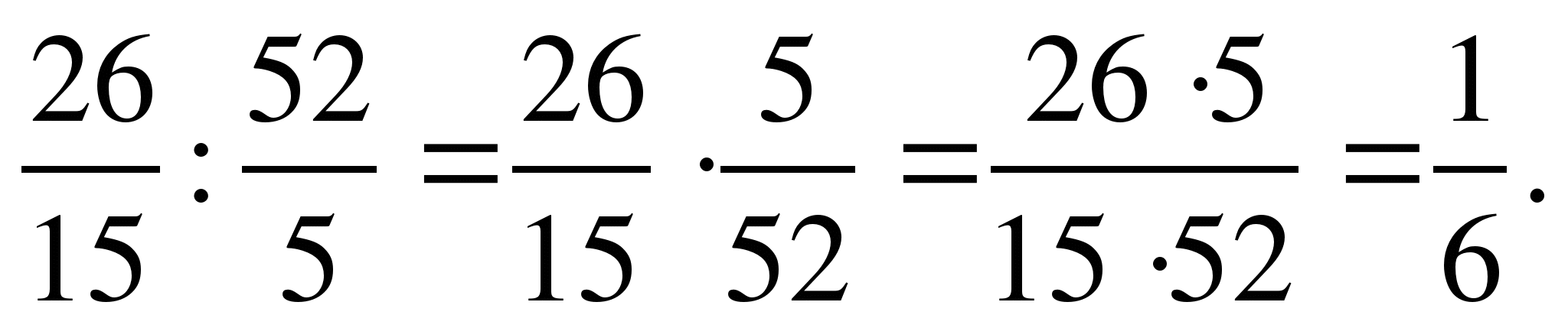
5 класс Смешанные дроби (памятка ученику)
Смешанные дроби
Смешанная Неправильная
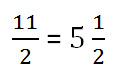
5 =
Сложение и вычитание смешанных дробей


Чтобы сложить смешанные числа, нужно:
1) привести к наименьшему общему знаменателю дробные части;
2) сложить отдельно целые и дробные части;
3) если необходимо, сократить дробную часть;
4) если дробная часть суммы окажется неправильной дробью, выделить из нее целую часть и полученное число прибавить к целой части суммы.
Например:
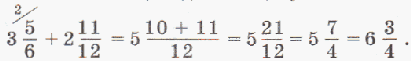
Чтобы вычесть смешанные числа, нужно:
1) привести к наименьшему общему знаменателю дробные части;
2) если дробные части «не вычитаются» (дробная часть уменьшаемого меньше дробной части вычитаемого),то нужно «занять» единицу из целой части;
3) вычесть отдельно целые и дробные части;
4) если необходимо, сократить дробную часть.
Например:
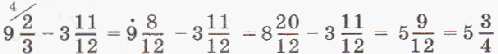
Например:
Смешанные дроби
Сложение:
1 шаг: к общ. знам. (НОЗ)
2 шаг: + цел1+цел2,
др1+др2 (числ1+числ2)
3 шаг: неправ. смеш.
4 шаг: сократить
Вычитание:
1 шаг: к общ. знам. (НОЗ)
2 шаг: занять ед. (если нужно)
3 шаг: — цел1 — цел2
др1 — др2 (числ1 — числ2)
4 шаг: сократить
Умножение:
1 шаг: смеш. неправ.
2 шаг: числ1 числ2
зн1 зн2 сократить!
3 шаг: вычислить
4 шаг: неправ. смеш.
Деление:
1 шаг: смеш. неправ.
2 шаг: числ1 зн2
зн1 числ2 сократить!
3 шаг: вычислить
4 шаг: неправ. смеш.
Обыкновенные дроби. Видеоурок. Математика 5 Класс
Слово «дробь» означает часть, нецелое количество, нецелое число.
Пол-литра молока. Для обозначения такого количества, для половины, мы используем дробь 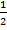 (рис. 1).
(рис. 1).
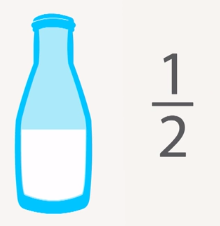
Рис. 1. 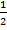 литра молока
литра молока
Треть пути. Если мы прошли треть пути, то мы знаем, что путь делится на три части и мы прошли одну такую часть (рис. 2).

Рис. 2. Треть пути
Одну часть мы обозначаем дробью  . Оставшийся путь составляет
. Оставшийся путь составляет  . Если весь путь был 6 км, то треть пути – это 2 км, оставшиеся
. Если весь путь был 6 км, то треть пути – это 2 км, оставшиеся  – это 4 км (рис. 3).
– это 4 км (рис. 3).
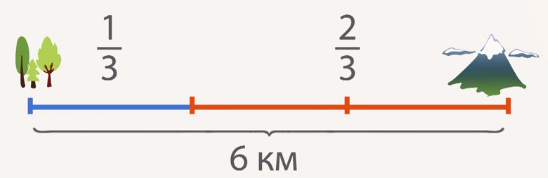
Рис. 3. Путь, разделенный на части
Четверть часа. Один час, то есть 60 минут, удобно делится на 4 части (рис. 4).

Рис. 4. Час, разделенный на четыре части
В каждой части по 15 минут. Одна такая часть называется четвертью. Обозначается как 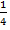 (рис. 5). Оставшаяся часть часа, 45 минут, содержит три таких четверти по 15 минут, обозначается
(рис. 5). Оставшаяся часть часа, 45 минут, содержит три таких четверти по 15 минут, обозначается 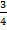 (рис. 6).
(рис. 6).
|
Рис. 5. Четверть часа
|
Рис. 6. Три четверти часа
|
Во всех этих примерах одинаковым было то, что мы брали объект (литр молока, путь, час) и делили на несколько равных частей. Потом брали одну или несколько таких частей и это количество и называли дробью.
Разделим торт на шесть равных частей. Каждая часть торта – это  торта (рис. 7).
торта (рис. 7).

Рис. 7. Торт, разделенный на шесть равных частей
Если взять две части торта, то получится 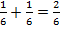 (две шестых) торта (рис. 8). А оставшаяся часть будет составлять
(две шестых) торта (рис. 8). А оставшаяся часть будет составлять 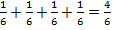 (четыре шестых) торта (рис. 9).
(четыре шестых) торта (рис. 9).
|
Рис. 8. Две шестых торта
|
Рис. 9. Четыре шестых торта
|
Какую часть торта означает дробь 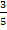 ?
?
Речь идет о пятых, значит, торт нужно разделить на пять частей (рис. 10) и взять три из них: 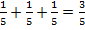 (рис. 11). Мы получаем чуть больше половины торта.
(рис. 11). Мы получаем чуть больше половины торта.
|
Рис. 10. Торт, разделенный на пять частей
|
Рис. 11. Три пятых торта
|
Не обязательно делить что-то целое, например торт, на части. Можно взять несколько предметов (множество) и разделить его на равные части.
Пусть есть 10 яблок (рис. 12). Разделим их на 5 равных частей, так как речь идет о пятых. Каждая часть будет состоять из двух яблок. Сама доля будет обозначаться 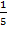 , ведь делили мы на 5 частей (рис. 13).
, ведь делили мы на 5 частей (рис. 13).
|
Рис. 12. Множество, состоящее из яблок
|
Рис. 13. Множество яблок, разделенное на пять частей
|
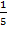 множества из 10 яблок будет содержать 2 яблока, а
множества из 10 яблок будет содержать 2 яблока, а 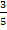 уже будет содержать 3 раза по 2 яблока, то есть 6 яблок.
уже будет содержать 3 раза по 2 яблока, то есть 6 яблок.
Не обязательно представлять конкретные объекты, как торт или множество яблок, чтобы работать с дробями. Можно оперировать с дробью как с математическим объектом.
Возьмем дробь  . Нижняя часть дроби, 7, называется знаменателем. Она сообщает, на сколько частей мы делили. Делили на 7 равных частей (рис. 14).
. Нижняя часть дроби, 7, называется знаменателем. Она сообщает, на сколько частей мы делили. Делили на 7 равных частей (рис. 14).

Рис. 14. Семь равных частей
Верхняя часть дроби, 3, называется числителем. Она сообщает, сколько таких частей мы взяли. То есть дробь  состоит из трех долей
состоит из трех долей  (рис. 15), полученных при делении на 7 равных частей.
(рис. 15), полученных при делении на 7 равных частей.

Рис. 15. Три доли, взятые из семи равных частей
Что означает дробь 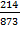 ? Нужно разделить объект на 873 равные части. Каждая часть – это
? Нужно разделить объект на 873 равные части. Каждая часть – это 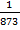 . Теперь нужно взять 214 таких долей.
. Теперь нужно взять 214 таких долей.
Потренируемся находить дроби от разных количеств.
В классе 30 человек.  класса пойдет на французский язык,
класса пойдет на французский язык,  класса – на английский. Сколько человек каким языком будет заниматься?
класса – на английский. Сколько человек каким языком будет заниматься?
Чтобы найти  от 30, нужно класс разделить на три равные части, то есть 30 разделить на 3. Тот факт, что мы ищем
от 30, нужно класс разделить на три равные части, то есть 30 разделить на 3. Тот факт, что мы ищем  от 30, будем записывать как
от 30, будем записывать как 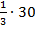 . Предлог «от» мы заменяем знаком умножения:
. Предлог «от» мы заменяем знаком умножения:
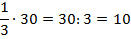
Полученное число 10 – это и есть доля  от общего количества учеников, от 30. Мы выяснили, что 10 учеников пойдут заниматься французским языком.
от общего количества учеников, от 30. Мы выяснили, что 10 учеников пойдут заниматься французским языком.
Найдем  общего количества учеников, то есть
общего количества учеников, то есть  от 30. Разделим 30 на 3 и умножим полученный результат на два.
от 30. Разделим 30 на 3 и умножим полученный результат на два.
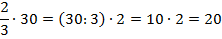
Найдем 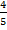 от общего количества учеников, то есть
от общего количества учеников, то есть 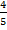 от 30 или
от 30 или 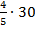 . Делим 30 на 5, получаем
. Делим 30 на 5, получаем 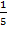 от 30, а именно 6. Тогда
от 30, а именно 6. Тогда 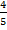 от 30 будет равна четырем таким долям, то есть 24.
от 30 будет равна четырем таким долям, то есть 24.
Давайте теперь сформулируем, как мы находили дробь для числа.
Пусть дано число 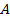 и необходимо найти его часть
и необходимо найти его часть 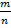 , то есть дробь
, то есть дробь 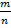 от
от 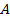 . Знаменатель говорит, на сколько частей надо делить, а числитель – сколько таких долей брать, умножать. То есть необходимо разделить
. Знаменатель говорит, на сколько частей надо делить, а числитель – сколько таких долей брать, умножать. То есть необходимо разделить 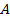 на
на 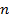 и умножить на
и умножить на 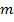 .
.
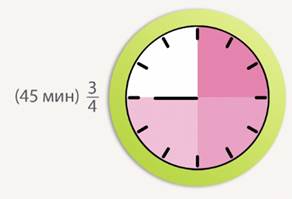
Сколько минут составляет 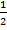 часа?
часа?  часа?
часа?  часа?
часа? 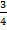 от трех часов?
от трех часов?
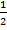 часа – это
часа – это 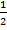 от 60 минут. Делим 60 на 2. Мы сразу получаем долю
от 60 минут. Делим 60 на 2. Мы сразу получаем долю 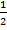 , это 30 минут. Или, как чаще говорят, полчаса. Половина часа.
, это 30 минут. Или, как чаще говорят, полчаса. Половина часа.
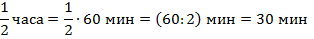
 от 60 минут. Делим 60 на 3 и умножаем на 2.
от 60 минут. Делим 60 на 3 и умножаем на 2.
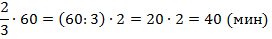
 от 60 минут. Делим 60 на 6. Получаем 10 минут, то есть
от 60 минут. Делим 60 на 6. Получаем 10 минут, то есть  часа. И умножаем на 5.
часа. И умножаем на 5.
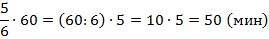
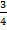 от трех часов. Три часа – это 180 минут, то есть ищем
от трех часов. Три часа – это 180 минут, то есть ищем 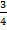 от 180. 180 делим на 4, то есть одна четверть от этого числа равна 45, и берем три таких части, умножаем на три.
от 180. 180 делим на 4, то есть одна четверть от этого числа равна 45, и берем три таких части, умножаем на три.
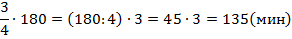
За три дня похода класс прошел 45 км. За первый день было пройдено  пути. За второй день
пути. За второй день 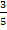 оставшегося пути. Сколько километров проходил класс в каждый из трех дней?
оставшегося пути. Сколько километров проходил класс в каждый из трех дней?
Весь путь – 45 км.
Первый день –  пути, то есть
пути, то есть  от 45 км.
от 45 км.
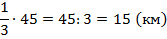
Второй день – 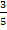 оставшегося пути. А какой путь остался? Так как в первый день прошли 15 км, то осталось
оставшегося пути. А какой путь остался? Так как в первый день прошли 15 км, то осталось 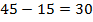 км.
км.
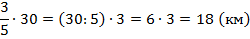
Третий день – весь оставшийся путь. Во второй день было пройдено 18 км из остававшихся 30. Значит, на третий день осталось 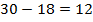 км.
км.
Еще раз повторим. Чтобы найти дробь от числа, от количества, нужно это число поделить на знаменатель нашей дроби и умножить на числитель.
Список литературы
- Зубарева И.И., Мордкович А.Г. Математика. 5 класс. – 14-е изд., испр. и доп. – М.: 2013. – 270 с.
- Мерзляк А.Г., Полонский В.Б., Якир М.С. Математика. 5 класс. – М.: 2014. – 304 с.
- Виленкин Н.Я., Жохов В.И. и др. Математика. 5 класс. – 24-е изд., испр. – М.: 2008. – 280 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Matematika-na.ru (Источник).
- Matematika-na.ru (Источник).
- Urokimatematiki.ru (Источник).
- Ppt4web.ru (Источник).
Домашнее задание
Вычислите:
 от 48
от 48 от 25
от 25 от двух часов
от двух часов от 27
от 27
Методическая разработка по математике (5 класс) на тему: Проверочная работа по математике для 5 класса по теме «Задачи на дроби. Нахождение части целого и целого по части»
СПЕЦИФИКАЦИЯ
проверочной работы по математике для 5 класса
по теме «Задачи на дроби. Нахождение части целого
и целого по части»
Разработка Зинченко Т.В.
1. Назначение проверочной работы
Работа предназначена для проведения процедуры тематического контроля индивидуальных достижений учащихся по математике по теме «Задачи на дроби. Нахождение части целого и целого по части». Основной целью работы является проверка и оценка способности обучающихся 5 класса применять полученные в процессе изучения математики знания для решения разнообразных задач учебного и практического характера.
2. Документы, определяющие содержание и характеристики проверочной работы
Содержание и основные характеристики проверочных материалов разработаны на основе следующих документов:
- Федеральный компонент государственного стандарта основного общего образования по математике (Приказ МО от 5 марта 2004 г. № 1089).
- О сертификации качества педагогических тестовых материалов (Приказ Минобразования России от 17.04.2000 г. № 1122).
3. Условия и время проведения проверочной работы.
На выполнение диагностической работы отводится 30 минут.
Дополнительных материалов и оборудования не требуется.
4. Содержание и структура проверочной работы
Каждый вариант диагностической работы состоит из 1 заданий: 5 заданий с выбором одного правильного ответа, 4 задания с кратким ответом и 2 задания с развёрнутым ответом.
В каждом варианте представлены как задания базового уровня сложности, так и задания повышенного уровня сложности (до 30% заданий).
Содержание диагностической работы охватывает основные элементы курса математики 5 класса. Работа может использоваться для контроля знаний при обучении по учебнику «Математика.5 класс» (авторы С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин)
Распределение заданий по проверяемым умениям представлено в таблице 1:
Таблица 1
№ п/п | Перечень проверяемых знаний и умений | Число заданий |
1 | Формулировать определение делителя и кратного | 2 |
2 | Формулировать определение простого и составного числа | 2 |
3 | Знать и использовать в решении признаки делимости чисел | 4 |
4 | Классифицировать натуральные числа по признакам делимости | 2 |
5 | Доказывать утверждения о делимости чисел | 1 |
6 | Решать задачи с использованием чётности и с делимостью чисел | 1 |
5. Система оценивания отдельных заданий и работы в целом
За правильное выполнение каждого из заданий 1-10 — ставится 1 балл.
За выполнение заданий 11,12 — ставятся 2 балла.
Всего – 14 баллов.
В Приложении 1 приведен план проверочной работы.
В Приложении 2 приведен календарно-тематический план.
Приложение 1
План проверочной работы
по математике в 5 классе
по теме «Признаки делимости. Простые и составные числа»
Используются следующие условные обозначения:
ВО – задание с выбором ответа, КО – задание с кратким ответом, РО – задание с развёрнутым ответом.
Б – базовый уровень сложности, П – повышенный уровень сложности.
Коды проверяемых умений приведены в соответствии с кодификатором МЦКО по математике для 5 класса.
№ зада-ния | Контролируемые элементы содержания | Проверяемые умения | Тип зада- ния | Время (мин) | Уро-вень слож-ности | Макс. балл |
1 | ВО | 1 | Б | 1 | ||
2 | ВО | 1 | Б | 1 | ||
3 | ВО | 2 | Б | 1 | ||
4 | ВО | 2 | Б | 1 | ||
5 | ВО | 2 | Б | 1 | ||
6 | ВО | 2 | Б | 1 | ||
7 | КО | 2 | Б | 1 | ||
8 | КО | 2 | Б | 1 | ||
9 | КО | 2 | П | 1 | ||
10 | КО | 2 | П | 1 | ||
11 | РО | 5 | П | 2 | ||
12 | РО | 5 | П | 2 |
Приложение 2
Математика 5 класс
к учебнику С.М. Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин «Математика 5» для общеобразовательных организаций
№ п/п | Раздел программы | количество часов | Характеристика основных учебных действий | |
1 | Натуральные числа и нуль | 52 | Описывать свойства натурального ряда. Читать и записывать натуральные чмсла, сравнивать их. Выполнять вычисления с натуральными числами; вычислять значения степеней. Формулировать законы арифметических действий, записывать их с помощью букв, применять их для рационализации вычислений. Анализировать и осмысливать текст задачи, извлекать необходимую информацию, моделировать условие с помощью схем, строить логическую цепочку рассуждений. Осуществлять самоконтроль, проверяя ответ на соответствие условию. Уметь решать задачи на понимание отношений «больше на…», «меньше на…», «больше в…», «меньше в…», а также понимание стандартных ситуаций, в которых используются слова «всего», «осталось» и т.п.; типовые задачи «на части», на нахождение двух чисел по их сумме и разности. | |
1.1 | Ряд натуральных чисел. | 1 | ||
1.2 | Десятичная система записи натуральных чисел. | 2 | ||
1.3 | Сравнение натуральных чисел. | 2 | ||
1.4 | Сложение. Законы сложения. | 3 | ||
1.5 | Вычитание. | 2 | ||
1.6. | Решение текстовых задач с помощью сложения и вычитания | 3 | ||
1.7 | Умножение. Законы умножения. | 2 | ||
1.8 | Распределительный закон. | 3 | ||
1.9 | Сложение и вычитание столбиком | 3 | ||
Контрольная работа №1. | 1 | |||
1.10 | Умножение чисел столбиком. | 3 | ||
1.11 | Степень с натуральным показателем. | 2 | ||
1.12 | Деление нацело. | 2 | ||
1.13 | Решение текстовых задач с помощью умножения и деления | 3 | ||
1.14 | Задачи на «части» | 5 | ||
1.15 | Деление с остатком. | 3 | ||
1.16 | Числовые выражения. | 2 | ||
Контрольная работа №2. | 1 | |||
1.17 | Задачи на нахождение двух чисел по их сумме и разности. | 5 | ||
1.18 | Дополнительный материал
| 1 3 | ||
2 | Измерение величин | 38 | Измерять с помощью линейки и сравнивать длины отрезков. Строить отрезки заданной длины с помощью циркуля и линейки. Выражать одни единицы измерения длины через другие. Представлять натуральные числа на координатном луче. Распознавать геометрические фигуры и приводить примеры аналогов из окружающего мира. Измерять с помощью транспортира и сравнивать величины углов. Строить углы заданной величины с помощью транспортира. Выражать одни единицы измерения углов через другие. Вычислять площади квадратов и прямоугольников, объёмы кубов и параллелепипедов, используя соответствующие формулы. Решать задачи на движение, на движение по реке. | |
2.1. | Прямая. Луч. Отрезок. | 2 | ||
2.2 | Измерение отрезков. | 2 | ||
2.3 | Метрические единицы длины. | 2 | ||
2.4 | Представление натуральных чисел на координатном луче. | 2 | ||
Контрольная работа №3. | 1 | |||
2.5 | Окружность и круг. Сфера и шар. | 1 | ||
2.6 | Углы. Измерение углов. | 3 | ||
2.7 | Треугольники. | 3 | ||
2.8 | Четырехугольники | 3 | ||
2.9 | Площадь прямоугольника. Единицы площади. | 3 | ||
2.10 | Прямоугольный параллелепипед | 2 | ||
2.11 | Объем прямоугольного параллелепипеда. Единицы объема. | 3 | ||
2.12 | Единицы массы | 1 | ||
2.13 | Единицы времени | 1 | ||
2.14 | Задачи на движение | 4 | ||
Контрольная работа №4 | 1 | |||
3 | Делимость натуральных чисел | 25 | Формулировать определение делителя и кратного, простого и составного числа, свойства и признаки делимости чисел, классифицировать натуральные числа (четные и нечетные, по остаткам от деления), Решать задачи, связанные с использованием четности и делимости чисел. | |
3.1 | Свойства делимости | 3 | ||
3.2 | Признаки делимости | 4 | ||
3.3 | Простые и составные числа. | 2 | ||
3.4 | Делители натурального числа. | 3 | ||
3.5 | Наибольший общий делитель | 4 | ||
3.6 | Наименьшее общее кратное | 4 | ||
Контрольная работа №5 | 1 | |||
Дополнительный материал 1.Использование четности и нечетности при решении задач 2.Исторические сведения 3.Занимательные задачи | 2 2 | |||
4 | Обыкновенные дроби | 75 | Преобразовывать обыкновенные дроби с помощью основного свойства дроби. Приводить дроби к общему знаменателю, сравнивать и упорядочивать их. Выполнять вычисления с обыкновенными дробями, использовать законы арифметических действий и уметь записывать их с помощью букв, применять их для рационализации вычислений. Решать задачи на дроби, на все действия с дробями, на совместную работу. Выражать с помощью дробей одни единицы измерения через другиеВыполнять вычисления со смешанными дробями, в том числе площадь и объем. Представлять дроби на координатном луче. | |
4.1 | Понятие дроби. | 1 | ||
4.2 | Равенство дробей. | 3 | ||
4.3 | Задачи на дроби | 5 | ||
4.4 | Приведение дробей к общему знаменателю. | 4 | ||
4.5 | Сравнение дробей | 3 | ||
4.6 | Сложение дробей | 3 | ||
4.7 | Законы сложения | 4 | ||
4.8 | Вычитание дробей. | 4 | ||
Контрольная работа № 6 | 1 | |||
4.9 | Умножение дробей | 4 | ||
4.10 | Законы умножения. | 2 | ||
4.11 | Деление дробей | 4 | ||
4.12 | Нахождение части целого и целого по части | 2 | ||
Контрольная работа № 7 | 1 | |||
4.13 | Задачи на совместную работу | 5 | ||
4.14 | Понятие смешанной дроби | 3 | ||
4.15 | Сложение смешанных дробей | 3 | ||
4.16 | Вычитание смешанных дробей | 4 | ||
4.17 | Умножение и деление смешанных дробей | 5 | ||
Контрольная работа №8 | 1 | |||
4.18 | Представление дробей на координатном луче | 4 | ||
4.19 | Площадь прямоугольника. Объём прямоугольного параллелепипеда | 3 | ||
Дополнительный материал 1.Сложные задачи на движение по реке 2.Исторические сведения 3.Занимательные задачи | 2 4 | |||
5 | Повторение курса математики 5 класса. | 14 | ||
Повторение | 13 | |||
Итоговая контрольная работа №9 | 1 | |||
Итого | 204 | |||
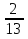 +
+ 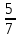 +
+ 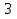 —
— 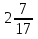
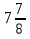 +
+ 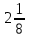
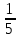 этого расстояния. Сколько километров осталось ему пройти?
этого расстояния. Сколько километров осталось ему пройти?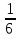 мячей, а зеленые –
мячей, а зеленые – 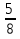 всех тракторов. Сколько всего было тракторов?
всех тракторов. Сколько всего было тракторов?






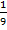 от 27
от 27