Логические задачи 5-6 классы
Задача 1
В пещере старый пират разложил свои сокровища в 3 цветных сундука, стоящих вдоль стены: в один — драгоценные камни, а в другой — золотые монеты, а в третий — оружие. Он помнит, что:
— красный сундук правее, чем драгоценные камни;
— оружие правее, чем красный сундук.
В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?
Решение:
Задача 2
Девять осликов за 3 дня съедают 27 мешков корма. Сколько корма надо пяти осликам на 5 дней?
Решение:
1 шаг 9 осликов в 1 день — 27 : 3= 9м.
2 шаг 1 ослик в 1 день — 9 : 9 = 1 м.
3 шаг 5 осликов в 1 день — 5 * 1 = 5 м.
4 шаг 5 осликов за 5 дней — 5 * 5 = 25 м.
Задача 3
Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за 0,5 секунды. Они одновременно стартовали от бассейна к эвкалипту по прямой. Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров
Решение:
1 шаг 240 : 3 = 80 (с) скакала мама Кенгуру
2 шаг сын за 0,5 с — 1 м, за 1 с — 2 м
3 шаг 80 * 2 = 160 (м) проскачет кенгурёнок за 80 с
4 шаг 240 — 160 = 80 (м) осталось проскакать кенгурёнку когда
мама уже под эвкалиптом
5 шаг 80 : 2 = 40 (с)
Ответ: 40 секунд
Задача 4
На скотном дворе гуляли гуси и поросята. Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84. сколько гусей и сколько поросят было на школьном дворе?
Решение:
1 шаг Представьте, что все поросята подняли по две ноги вверх
2 шаг на земле осталось стоять 30 * 2 = 60 ног
3 шаг подняли вверх 84 — 60 = 24 ноги
4 шаг подняли 24 : 2 = 12 поросят
5 шаг 30 — 12 = 18 гусей
Ответ: 12 поросят и 18 гусей.
Аналогичная задача: Сколько на лугу коров и гусей, если у них вместе 36 голов и 100 ног. (14 коров, 22 гуся)
Задача 5
На книжной полке можно разместить либо 25 одинаковых толстых книг, либо 45 тонких книг. Можно ли разместить на этой полке 20 толстых книг и 9 тонких книг?
Решение:
1 шаг. Заметим, что и 25 и 45 делятся на 5
25: 5 = 5(к) толстых
45 : 5 = 9 (к) тонких
2 шаг обратить внимание на то, что 5 толстых книг занимает столько же места сколько 9 тонких
3 шаг вывод на 20 толстых книг и 9 тонких — места хватит
Задача 6
Можно ли семь телефонов соединить между собой попарно так, чтобы каждый был соединён ровно с тремя другими?
(7* 3 = 21, число нечётное, нельзя)
Задача 7
Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов?
Решение:
Перевернуть обои часы. Когда пройдёт 3 минуты в семиминутных часах останется 4 минуты. Поставьте яйца в это время вариться. Когда 4 минуты закончатся, перевернуть семиминутные часы обратно 4 + 7 + 11 мин.
Задача 8
В ящике лежат шары: 5 красных, 7 синих и 1 зелёный. Сколько шаров надо вынуть, чтобы достать два шара одного цвета?
Решение:
подумайте сколько всего шаров различных цветов можно достать не повторяясь (3)
Ответ: надо вынуть 4 шара
Задача 9
Известно, что P — 2 = Q + 2 = X — 3 = Y + 4 = Z — 5
Решение:
Обращаем внимание учащихся на, то что в каждом случае происходило с числами т.е. Р уменьшили на 2, чтобы сравнять с остальными числами и т.д. В ходе дальнейших рассуждений видим, что Y увеличили на 4, т.е. оно было самым маленьким.
Задача 10
Двум парам молодоженов нужно переправиться на другой берег. Для этого имеется двуместная лодка, но сложность состоит в том, что молодые жены отказались оставаться в обществе незнакомого мужчины без своего мужа. Как осуществить переправу всех четверых, соблюдая это условие?
Решение:
М1М2
М1
Ж1Ж2
Ж1
М1Ж1
Ответ: за 5 переездов.
Задача № 1 :
Разность двух чисел на 17 меньше уменьшаемого и на 9 больше вычитаемого.
Найдите уменьшаемое и вычитаемое.
Задача № 2 :
Будет ли сумма чисел 1 + 2 + 3 + ……+ 2005 + 2006 + 2007 делиться на 2007?
Ответ обоснуйте.
Задача № 3 :
Нужно разместить 17 кроликов так, чтобы в каждой клетке было разное количество кроликов.
Какое наибольшее число клеток понадобится?
Задача № 4 :
На выставку привезли 25 собак. 12 из них большие, 8 маленькие, остальные средние.
Только 10 из участников выставки породистые, остальные дворняжки.
Среди дворняжек поровну больших, маленьких и средних.
Сколько больших породистых собак привезли на выставку?
Задача № 5 :
Все треугольники, изображенные на рисунке, имеют равные стороны.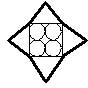
Радиус каждой из окружностей равен 2 см.
Окружности касаются друг друга и сторон квадрата.
Чему равен периметр звездочки, нарисованной жирной линией?
Ответы :
№ 1 : Ответ: 43 – 17.
№ 2 : Ответ: будет.
Представим данную сумму в виде следующих слагаемых: (1 + 2006) + (2 + 2005) + …..+ (1003 + 1004) + 2007.
Так как каждое слагаемое делится на 2007, то и вся сумма будет делиться на 2007.
№ 3 : Ответ: 5 клеток.
№ 4 : Ответ: 7 больших породистых собак.
№ 5 : Ответ: 64 см
На некотором острове необычайно регулярный климат по понедельникам и средам всегда идут дожди,по субботам — туман, зато в остальные дни — солнечно.
Утром какого дня недели нужно начать свой отдых группе туристов, если они хотят пробыть там 44 дня и захватить при этом как можно больше солнечных дней?
A — в понедельник; B — в среду; C — в четверг; D — в пятницу; E — во вторник
Решение:Выясним, сколько полных недель в 44 днях.
Получим 6 недель. В течении этих недель число солнечных дней не зависит от того, когда начнется отдых. В качестве оставшихся двух дней выбираем четверг и пятницу — солнечные дни.
Следовательно, отправляем туристов утром в четверг.
То есть верный ответ — (С).
Задача № 2 :
У двузначного числа «n» цифра десятков в два раза больше, чем цифра единиц.
Тогда число «n» обязательно: A — четное; B — нечетное; C — меньше 20; D — делится на 3; E — делится на 6.
Решение :
Ищем число «n» среди ряда чисел: 10 — 99.
По условию, у всех подозреваемых чисел — десятки четны (2,4,6,8), а единицы — в два раза меньше (1,2,3,4,). Перечислим все эти числа: 21, 42, 63, 84. Все они делятся на 3.
Следовательно верен ответ (D).
Задача № 3 :
Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18. На какое число делили? A — 18; B — 32; C — 24; D — 36; A — 48;
Решение :
Из условия следует, что 100-4=96 делится на искомое число.
Также 90-18=72 делится на искомое число.
Их разность также делится на искомое число: 96-72=24.
Следовательно, искомое число — 24, так как на него делится и 96, и 72.
Верен ответ (С).
Задача № 4:
Раньше называли число, равное миллиону миллионов, словом «легион». Если разделить миллион легионов на легион миллионов, то получится: A — легион; B — миллион; C — миллион миллионов; D — легион легионов; E — 1
Решение:
Перепишем заново:
делимое: миллион легионов — это миллион миллионов миллионов,
делитель: легион миллионов — это миллион миллионов миллионов,
следовательно частное равно 1.
Верен ответ (Е).
Логические задачи для учащихся 5, 6 классов
ЛОГИЧЕСКИЕ ЗАДАЧИ ДЛЯ 5 КЛАССА С ОТВЕТАМИ
1. Пять землекопов за 5 часов выкапывают 5 м канавы.
Сколько потребуется землекопов, для того чтобы выкопать 100 м канавы за 100 часов?
Ответ: Понадобятся те же пять землекопов, не больше.
2. В самом деле, пять землекопов за 5 часов выкапывают 5 м канавы; значит, пять землекопов за 1 час вырыли бы 1 м канавы, а в 100 часов — 100 м. Люди, приезжавшие в одну деревушку, часто удивлялись местному дурачку.
Когда ему предлагали выбор между блестящей 50-центовой монетой и мятой пятидолларовой купюрой,
он всегда выбирал монету, хотя она стоит вдесятеро меньше купюры.
Почему он никогда не выбирал купюру?
Ответ: «Дурачок» был не так глуп: он понимал, что, пока он будет выбирать 50-центоную монету, люди будут предлагать ему деньги на выбор,
а если он выберет пятидолларовую купюру, предложения денег прекратятся, и он не будет получать ничего.
3. Образно представьте себе нашу планету, плотно стянутую кольцом по всему ее экватору.
После увеличения длины окружности кольца на 10 метров,
между кольцом и поверхностью земли образовался зазор определенной величины.
Как Вы считаете, сможет ли человек пройти, или хотя бы протиснуться в этот зазор?
Известно, что экватор имеет длину приблизительно равную 40 000 километров.
Ответ: Для решения данной задачи достаточно элементарных знаний геометрии.
Изначально может показаться, что увеличение длины кольца на 10 метров,
по сравнению с его длиной в 40 000 км будет способствовать образованию практически незаметного зазора.
Однако, исходя из формулы определения длины окружности L = 2П * R видно, что радиус Земли (кольца) R = L/2П и при увеличении длины кольца на 10м,
его радиус приблизительно увеличиться на 1,59м (10м / 6,28), образуя соответствующий зазор,
в который человек сможет не только протиснуться, но и даже пройти, немного нагнувшись.
4. Пете и Коле купили по коробке конфет. В каждой коробке находится 12 конфет.
Петя из своей коробки съел несколько конфет, а Коля из своей коробки съел столько конфет, сколько осталось в коробке у Пети.
Сколько конфет осталось на двоих у Пети и Коли?
Ответ: 12 конфет.
5. Человек живет на 17-м этаже.
На свой этаж он поднимается на лифте только в дождливую погоду или тогда, когда кто-нибудь из соседей с ним едет в лифте.
Если погода хорошая и он один в лифте, то он едет до 9-го этажа, а дальше до 17-го этажа идет пешком по лестнице. Почему?
Ответ: Этот человек — лилипут, и до кнопки 17-го этажа дотягивается только зонтиком или просит кого-нибудь нажать на эту кнопку.
6. Инспектор, проверявший некую школу, заметил, что, когда бы он ни задал классу вопрос, в ответ тянули руки все ученики.
Более того, хотя школьный учитель каждый раз выбирал другого ученика, ответ всегда был правильным. Как это получалось?
Ответ: Учитель предварительно договорился с учениками, чтобы они вызывались отвечать независимо от того, знают ответ или не знают. Но те, кто знает ответ, должны поднимать правую руку, а те, кто не знает, — левую. Учитель каждый раз выбирал другого ученика, но всегда того, кто поднимал правую руку.
7. У Вас есть два шнура (фитиля).
Каждый шнур, подожженный с конца, полностью сгорает дотла ровно за один час, но при этом горит с неравномерной скоростью.
Как при помощи этих шнуров и зажигалки отмерить время в 45 минут?
Ответ: Необходимо поджечь первый шнур одновременно с обоих концов — получаем 30 минут. Одновременно с первым шнуром поджигаем второй шнур с одного конца, и когда первый шнур догорит (30 минут),- поджигаем второй шнур с другого конца (оставшиеся 15 минут).
8. Возвращаясь с рыбалки домой, рыболов встретил своего приятеля, который поинтересовался его уловом.
Но, так как наш рыболов помимо рыбалки был также большим любителем всякого рода загадок, ответил приятелю следующим образом: «Если к количеству пойманной мною рыбы добавить половину улова и еще десяток рыбин, то мой улов составил бы ровно сотню рыб». Сколько рыбы поймал рыболов?
Ответ: Решим задачу с ее конца. Отнимем лишние 10 рыб — останется 90 рыб. В число 90 заключены три равные части, из которых две являются действительным уловом, а третья — дополнительной половиной от действительного улова. Следовательно, эта дополнительная половина улова составляет 90:3=30 рыб, а сам улов 30х2=60 рыб.
9. Воздушный шар уносится непрерывным ветром в южном направлении.
В какую сторону развиваются при этом флаги на его гондоле?
Ответ: Шар, уносимый воздушным течением, находится по отношению к окружающему воздуху в покое; поэтому флаги не станут развиваться на ветру ни в какую сторону, а будут свисать, вниз, как в безветрие.
10.Считается, что есть веская причина, по которой у птичьих яиц один конец тупее другого. Что это за причина?
Ответ: Сферические и овальные яйца катились бы по прямой. Асимметричные же яйца, у которых один конец тупее, а другой острее, при скатывании стремятся катиться по кругу. Если яйцо лежит на краю обрыва или в другом ненадежном месте, стремление катиться по кругу, а не по прямой — большое преимущество.
11. Имеется круглое глубокое озеро диаметром 200 метров и два дерева,
одно из которых растет на берегу у самой воды,
другое — по центру озера на небольшом островке.
Человеку, который не умеет плавать, нужно перебраться на островок при помощи веревки, длина которой чуть больше 200 метров.
Как ему это сделать?
Ответ: Привязав веревку одним концом к дереву, растущему на берегу, необходимо обойти с веревкой озеро по окружности и привязать второй конец веревки к тому же дереву. В результате между деревьями будет натянута сдвоенная веревка для переправы на остров.
12. Трехзначное число состоит из возрастающих (слева направо) цифр.
Если это число прочитать, то все слова будут начинаться на одну и туже букву. Что это за число?
Ответ: 147.
13. На обыкновенных чашечных весах лежат:
на одной чашке — булыжник, весящий ровно 2 кг, на другой — железная гиря, весящая так же 2 кг.
Весы осторожно опустили под воду. Остались ли чашки в равновесии?
Ответ: Каждое тело, если погрузить его в воду, становится легче: оно «теряет» в своем весе столько, сколько весит вытесненная им вода. Булыжник весом в 2 кг занимает больший объем, чем 2-х килограммовая железная гиря, потому, что материал камня легче железа. Значит, булыжник вытеснит больший объем воды, нежели гиря, и по закону Архимеда потеряет в воде больше веса, чем гиря. Следовательно, весы под водой наклонятся в сторону гири.
14. Предположим Вам надо повалить бетонную стену длиной в 20 метров, высотой в 3 метра и весом в 3 тонны.
Как вы выполните эту задачу, если в вашем распоряжении нет абсолютно никаких инструментов?
Ответ: Такая стена, при таком весе и заданных размерах, будет иметь толщину лишь около 2 сантиметров и легко может быть повалена рукой.
15. Человек прыгает со стула. В руках он держит весы, на чашке которых лежит груз 10 кг.
На каком делении будет стоять стрелка весов во время падения?
Ответ: На нуле.
16. На гладкую доску положили 2 кирпича — один плашмя, а другой на ребро. Кирпичи весят одинаково.
Какой кирпич соскользнет первым, если наклонять доску?
Ответ: Кирпичи начнут скользить одновременно. Ведь оба кирпича давят на доску с одинаковой силой, а значит, одинаковы и силы трения, которые приходится им преодолевать. Удельные силы трения, приходящиеся на каждый квадратный сантиметр площади соприкосновения кирпичей с доской, конечно, не равны. Но общие силы трения, действующие на кирпичи, равные произведению удельной силы трения на площадь поверхности соприкосновения, будут одинаковы.
17. Все мы неоднократно слышали журчание ручья. Как Вы считаете, отчего он журчит?
Ответ: Ручей журчит оттого, что струя воды при небольшом падении захватывает частицы воздуха и погружает их в воду, отчего образуются пузырьки. Лопаньем этих пузырьков и объясняется журчание ручья.
20.Для чего между рельсами оставляют зазоры?
Ответ: Между стыками рельсов всегда оставляют пустые промежутки — зазоры. Делается это специально. Если зазоров не оставить и укладывать рельсы вплотную один к другому, железная дорога скоро придет в негодность. Дело в том, что все предметы при их нагревании раздаются во все стороны. Удлиняется и стальной рельс летом, когда его нагревает солнце. Если же не дать рельсам простора для удлинения, то, упираясь концами друг в друга с большой силой, они изогнутся вбок, вырвут удерживающие их костыли и исковеркают путь. В зимнюю пору происходит противоположное — сжатие рельса.
13. В больницу Сент-Джеймс направляли всех пострадавших в результате несчастных случаев в городе.
Больше всего было водителей и пассажиров, пострадавших в ДТП.
Чтобы уменьшить их число, городские власти сделали обязательным пользование ремнями безопасности.
Водители и пассажиры стали пристегиваться этими ремнями, но число ДТП осталось неизменным, а число пострадавших в них людей,
которые поступали в больницу, даже увеличилось. Почему?
Ответ: Пользование ремнями безопасности уменьшило число погибающих при ДТП. Многие люди, которые без ремня безопасности погибли бы (и попали бы в морги), оставались в живых, но получали травмы, и им требовалось лечение. Поэтому число попадающих в больницу стало больше.
14. 15. Мужчина ночью долго ворочался в кровати и никак не мог заснуть…
Потом он взял телефон, набрал чей-то номер, прослушав несколько длинных гудков — положил трубку и спокойно заснул.
Вопрос: почему он до этого не мог заснуть?
Ответ: За стеной громко храпел сосед, который потом проснулся от телефонного звонка.
С борта парохода был спущен стальной трап. Нижние 4 ступеньки трапа погружены в воду.
Каждая ступенька имеет толщину в 5 см; расстояние между двумя соседними ступеньками составляет 30 см.
Начался прилив, при котором уровень воды стал поднимается со скоростью 40 см в час.
Как Вы считаете, сколько ступенек окажется под водой через 2 часа?
Ответ: Через два часа под водой будут те же 4 ступеньки, потому что во время прилива лестница поднимается вместе с пароходом.
Логические задачи
1. Отправился человек в море и попал в шторм. Его отнесло на остров, где не было мужчин, а жили только девушки. Утром проснулся мужик на каком-то ритуале, весь обвязанный веревками, и узнал, что его хотят убить. Тогда попросил бедолага дать ему последнее слово. После того, как мужчина произнес его, девушки смастерили ему лодку, дали еду и отправили домой. Что же он сказал?
2. Эту загадку ученик первого класса решает за 5 минут, старшеклассник справляется за 15 минут, студент — за час, профессор же не решит никогда. А вот и вся головоломка: расшифруй ОДТЧПШСВДД.
3. Один поезд едет из Москвы в Санкт-Петербург с опозданием в 10 минут, а другой — в обратном направлении с опозданием в 20 минут. Какой из этих поездов будет ближе к Москве, когда они встретятся?
4. Известно, что среди девяти монет есть одна фальшивая, вес которой меньше, чем у остальных. Как с помощью чашечных весов всего за два взвешивания определить фальшивку?
5. Стоит стена из бетона высотой 3 метра, длиной 20 метров и весом 3 тонны. Как ее повалить, не имея никаких вспомогательных средств и инструментов?
6. Кошка – 3, лошадь – 5, петух – 8, ослик – 2, кукушка – 4, лягушка – 3, собака — ?
7. К реке подходят два человека. У берега стоит лодка, которая может выдержать только одного. Оба человека переправились на противоположный берег. Как?
8. Где встречается такое, что конь через коня перепрыгивает?
9. Шерлок Холмс шел по улице. И вдруг он увидел мертвую женщину, лежащую на земле. Сыщик подошел, открыл ее сумку и достал телефон. В телефонной книге нашел номер ее мужа и позвонил. Шерлок сказал: «Срочно приезжайте сюда. Ваша жена умерла». Через некоторое время приезжает муж, смотрит на жену и говорит: «Милая моя, что с тобой случилось?» Вскоре подоспела полиция. Шерлок указал пальцем на мужа женщины и промолвил: «Арестуйте этого человека, он убил свою жену». Вопрос: почему Шерлок так подумал?
10. Отец с двумя сыновьями отправился в поход. На их пути встретилась река, у берега которой находился плот. Он выдерживает на воде или отца, или двух сыновей. Как переправиться всем на другой берег?
Ответы.
1. Пусть меня убьет самая некрасивая.
2. 1, 2, 3, 4…
3. В момент встречи они будут на одинаковом расстоянии от Москвы.
4. Первое взвешивание: на каждой чаше весов по 3 монеты. Фальшивка находится в той кучке, которая меньше весит. Если равны, то фальшивая монета в третьей партии. Второе взвешивание: из тройки с наименьшим весом берем две монеты и взвешиваем. Какая чаша опуститься меньше, там и подделка. Если чаши весов равны, то фальшивка — оставшаяся монета из этой партии.
5. Толщина такой стены будет не более двух сантиметров, что позволяет толкнуть ее рукой.
6. Кошка говорит мяу (3 буквы), лошадь — и-го-го (5 букв), петух — ку-ка-ре-ку (8)… Собака, как известно, — гав, поэтому правильный ответ 3.
7. Они просто были на разных берегах.
8. В шахматах.
9. Ведь Холмс не назвал адрес, куда ехать.
10. Сперва переправляются оба сына. Один из них возвращается обратно к отцу. Папа перебирается на противоположный берег к сыну и остается на берегу, а второй сын переправляется на исходный берег за братом, после чего они оба переправляются к отцу.
1.Ответ:
Всего 5 остановок (включая конечную).
2.Ответ
На эскалаторе 280 ступеней.
Если общее количество ступеней на открытой части эскалатора обозначить через N, то при движении вниз оно будет складываться из количества ступеней, на которые опустился сам эскалатор, и количества ступеней, пройденных по нему. В первом случае время движения составило 140 : 2 = 70 секунд, во втором — 56 секунд. Для постоянной скорости эскалатора V указанные соображения приводят к уравнениям:
140 + 70*V = N
168 + 56*V = N,
решение которых N = 280 ступеней и V = 2 ступени в секунду.
3.Ответ
У кого-то может денег не быть!
1 — 1,54
2 — 1,35
3 — 0
4.Ответ:
Пусть велосипедист вёз мальчика х километров. Скорость мальчика v км/ч, скорость велосипедиста 2v км/ч. Между 12-00 и 14-00 прошло времени x/2v+a/v=(x+2a)/(2v)=2 часа. На обратную дорогу уйдёт (x+2a)/v=4 часа
5.Ответ:
12345 23456 34567 45678 56789
и обратные:
98765 87654 76543 65432 54321
и одно 55555
1.Прочитайте условие, но только один раз, и попробуйте сразу же ответить на вопрос. На конечной остановке в автобус сели четырнадцать мужчин и две женщины. На первой остановке сошли двое мужчин и вошли две женщины. На следующей остановке вышли почти все мужчины (осталось только трое), а на следующей вошли пять женщин. Проехав с полкилометра, автобус остановился, и в него вошел еще один мужчина. Сколько всего было остановок на пути следования автобуса?
2.Человек опаздывал на работу и, чтобы наверстать потерянное в пробке время, побежал вниз по эскалатору метро. Спускаясь со скоростью две ступени в секунду, он насчитал сто сорок ступеней. Через день ситуация повторилась, но теперь ему грозило большее опоздание. Естественно, по тому же эскалатору он бежал быстрее — со скоростью три ступени в секунду, а насчитал на двадцать восемь ступенек больше.
Странно получилось: чем быстрее бежишь, тем длиннее эскалатор.
Сколько же всего ступенек на нем?
3. Трое друзей хотят купить книжку. Оказалось, что двоим на покупку книги не хватает 1 копейки, третьему 2 рубля 90 копеек. Когда они сложили свои деньги, то денег на покупку книги им все равно не хватило. Зная, что денег у первого из друзей на 19 копеек больше чем у второго, найдите, сколько денег было у каждого.
4. Мальчик пошел из лагеря в город. В 12 часов, в нескольких километрах от лагеря, его догнал велосипедист и подвез его немного. Затем велосипедист высадил мальчика недалеко от города, и в 14 часов мальчик добрался до города.
Сколько времени потратит мальчик на обратную дорогу пешком, если известно, что скорость велосипедиста в два раза больше скорости мальчика?
5. На доске выписаны все пятизначные числа, у которых каждая цифра либо равна обеим соседним, либо отличается от соседних ровно на единицу — от одного в меньшую, а от другого в большую сторону.
Сколько написанных на доске чисел содержат в своей записи цифру 5?
Задачи на взвешивание и переливания.
1.Есть 10 мешков с золотом. В каждом по 10 монет. В девяти мешках монеты настоящие, а в одном — все фальшивые. Одна настоящая монета весит 5 грамм, а фальшивая — 4 грамма. Есть весы, показывающие вес в граммах.
Необходимо за одно взвешивание точно определить, в каком мешке фальшивые монеты
Мешки можно раскрывать и вытаскивать монеты
2. Как, имея пятилитровое и девятилитровое ведро, набрать из крана ровно три литра воды?
3.Винодел обычно продает свое вино по 30 и по 50 литров и использует для этого кувшины только такого размера. Один из покупателей захотел купить 10 литров. Как винодел отмерил ему 10 литров пользуясь своими кувшинами?
4.Как из полного сосуда ёмкостью в 12 л отлить половину, пользуясь двумя пустыми сосудами ёмкостью в 8 и 5 л.
5.Три человека купили сосуд, полностью заполненный 24 унциями меда. Позже они приобрели три пустых сосуда объемом 5, 11 и 13 унций. Как они могли бы поделить мед на равные части используя эти четыре сосуда? Постарайтсь решить задачу за наименьшее количество переливаний.
Восемнадцать спичек образовывают 6 одинаковых прилегающих друг к другу квадратов. Заберите 2 спички так, чтобы осталось 4 таких же квадрата.
11.Что больше: сумма всех цифр или их произведение?
12.Как разделить 5 яблок между пятью лицами так, чтобы каждый получил по яблоку и одно яблоко осталось в корзине.
13.В тот день в классе было 24 человека. Когда ученики писали контрольную работу, то они по мере завершения клали тетради в стопку одна на другую. Петя сдал тетрадь пятым по счёту. Каким по счёту его тетрадь проверят, если считать, что учитель проверяет тетрадь сверху стопки и строго по порядку?
1.Ответ:
Пронумеруем мешки от 1 до 10. Вытащим из первого 1 монету, из второго 2, из третьего 3 и так далее. Затем возьмем всю эту кучу монет и положим на весы. Если бы они все были настоящие, то общий вес составил бы 275 грамм (т.к. мы вытащили в общей сложности 55 монет). Но в одном из мешков были фальшивые. Если это был первый мешок, то вес будет на 1 грамм меньше (т.к. мы взяли оттуда 1 монету). Если фальшивые были во втором, то на 2 грамма меньше. И так далее.
2.Ответ:
Заполняем 9-литровое ведро и заливаем из него в 5-литровое ведро. (Далее 5-литровка и 9-литровка). в 9-литровке 4 литра. Выливаем воду из 5-литровки и заливаем туда 4 литра из 9-литровки. Заполняем 9-литровку и выливаем оттуда 1 литр в пятилитровку. Выливаем воду из 5-литровки, и заполняем пятилитровку из девятилитровки. Всё! В девятилитровке теперь 3 литра.
3.Ответ:
Сначала он наполнил 30-литровый кувшин и вылил его содержимое в 50-литровый. Потом опять наполнил 30-литровый и долил до полного заполнения в 50-литровый. В результате у него в кувшине останется 10 литров.
4.Ответ:
Сначала наливаете 8 литров в 8л., потом из 8л. наливаете полный 5л., в результате получается, что в 12л.- 4 литра, в 8л — 3литра, а в 5л.- 5 литров. Переливаете из 5л. в 12л. всю воду, а из 8л. переливаете все 3 литра в 5л. В результате 9 литров в 12л, 0 литров в 8л., и 3 литра в 5л. Переливаете из 12л. 8 литров в пустой 8л.,и в 12 л. остается 1 литр. Из 8л. доливаете в 5л., пока 5л. не станет полным, (в 5л. было 3л., след. долили мы еще 2литра из 8л.) Тогда в 8л. как раз остается 6л.
5.Ответ:
Сосуды могут содержать 24, 13, 11, и 5 унций соответственно:
Их начальное состояние 24, 0, 0, 0;
1 — 8, 0, 11, 5;
2 — 8, 11, 0, 5;
3 — 8, 13, 3, 0;
4 — 8, 8, 3, 5;
5 — 8, 8, 8, 0.
6. Ответ:
11.Ответ:
Больше сумма, так как произведение равно 0 (один из множителей — это цифра 0).
12.Ответ:
Один человек берет яблоко вместе с корзиной.
13.Ответ:
Подвох в том, что учитель тоже человек. Т.е. в классе было 23 ученика, и после Пети работу сдали 18 человек (23-5). Таким образом, Петину тетрадь проверят 19-ой.
Логические задачи для 8 класса с ответами
Логические задачи для 8 класса с ответами
#1
Как вы думаете, какой предмет будет иметь одинаковое изображение при рисовании его с любой точки зрения?
Ответ?
Этим свойством обладает только шар
#2
Если три десятка умножить на четыре десятка, то сколько получится?
Ответ?
Получится не 12 десятков, а 120 десятков. То есть: 30 * 40 = 1200
#3
Ответьте, сколько сейчас времени, если оставшаяся часть суток в два раза превышает прошедшую?
#4
Попробуйте догадаться сколько стоит книга, если книга стоит доллар плюс пол книги.
Ответ?
Книга стоит 2 доллара. Решение: полкниги стоит доллар, значит вся книга стоит 2 доллара
#5
Некий бизнесмен захотел привезти в Японию для продажи 10 000 пар первоклассных дорогих кроссовок.
Но в Японии на такие кроссовки накладываются очень большие пошлины.
Подумайте и скажите, как же хитроумный бизнесмен смог ввезти все эти кроссовки в Японию, при этом заплатил только очень небольшие деньги? Никакой коррупционной и преступной составляющей здесь нет.
Ответ?
Бизнесмен поступил очень хитро. Он разделил каждую пару кроссовок и отправил весь объем двумя партиями.
То есть в одной партии были только кроссовки на левую ногу, во второй только на правую ногу. Одну партию он отправил в Токио, другую в Осака.
В каждом из городов бизнесмен не заплатил пошлину и товары были конфискованы и выставлены на аукционе.
В связи с тем, что никому не была нужна партия кроссовок только на одну ногу, то бизнесмен выкупил сам обе партии за мизерные деньги.
#6
В мешке имеется 9 кг сахара. Есть также и две гири по 50г и 200г.
Подумайте, как за три взвешивания на чашечных весах отвесить 2кг сахара?
Ответ?
Сперва необходимо на чашечных весах разделить содержимое мешка пополам на 4,5кг в каждой чашке.
Далее одну чашу опустошаем, и снова 4,5кг делим пополам и получаем в каждой чаше весов по 2, 25кг.
В третье взвешивание уже нужно опустошить обе чаши, но из одной чаши 2,25кг сахара положить в отдельный мешок.
И далее при помощи гирек в 200г и 50г (итого 250г) отвесить из пакета с 2,25кг ровно 250г. Тогда в пакете останется ровно 2 кг.
#7
5 рыбаков съели 5 карпов за 5 дней. Как вы думаете, а за сколько дней 15 рыбаков съедят 15 карпов?
Ответ?
15 рыбаков съедят 15 карпов тоже за 5 дней. Если 5 рыбаков съедают 5 карпов за определенный промежуток времени, то у 15 рыбаков скорость поедания карпов в 3 раза больше, следовательно за 5 дней они съедят 15 карпов
#8
Два колхозника решили узнать, у кого больше овец.
Первый из них сказал: «если ты дашь мне свою козу, то у меня будет их в два раза больше, чем у тебя». Второй ему говорит: «А давай лучше ты мне дашь свою одну овцу, тогда у меня овец будет столько же, сколько и у тебя». Сколько же овец у каждого из колхозников? (Передачи овец пока еще не было)
Ответ?
У первого колхозника 7 овец, у второго только 5.
Если первый колхозник отдает одну овцу второму и их становится поровну, то значит, что изначально у первого их на 2 больше.
Если же второй колхозник отдает овцу первому, то их становится у первого в 2 раза больше, такое возможно, только если у первого изначально было 7 овец, а у второго 5
#9
Как вы думаете, сколько граней имеет шестигранный карандаш, который ни разу не затачивали?
Ответ?
Шестигранный карандаш, если не подвергался заточке будет иметь 8 граней. 6 большие грани и 2 торцевые.
#10
Можете ли вы обосновать, почему почти во всех странах мира канализационные крышки у люков имеют только круглую форму? (Квадратные крышки люков бывают лишь тогда, когда они дополнительно крепятся шарнирами)
Ответ?
Если крышки люков будут квадратными, то они могут легко провалиться в люк, т.к. диагональ квадрата больше стороны квадрата.
Поэтому их если и делают, то только прикрепив к люку шарнирами.
У круглых крышек люков нет диагонали и стороны, а только диаметр, который у крышки всегда больше отверстия люка
#11
Попробуйте сообразить, какой из выводов, указанных ниже, верный:
А) Здесь три ложных вывода.
Б) Здесь один ложный вывод.
В) Здесь два ложных вывода.
Г) Здесь пять ложных выводов.
Д) Здесь четыре ложных вывода.
Ответ?
Правильный вариант Д — здесь четыре ложных вывода. В связи с тем, что один является верным, а остальные не верные
#12
Можете ли вы записать число 1000 при помощи только восьми восьмерок и арифметических знаков суммы?
Ответ?
Получится равенство: 888 + 88 + 8 + 8 + 8 = 1000
#13
В одном классе всего 36 учеников. Девочек на 3 больше, чем мальчиков. Сколько мальчиков и девочек в этом классе?
Ответ?
Если разделить 36 пополам, то получим 18, т.е. две половины класса по 18 человек.
Если из первой половины добавить школьника в другую, то получится разница в 2 человека.
Если отнять еще одного и добавить снова в большую часть, то получим превышение на 4 человека. Следовательно задача не имеет решения
#14
На столе лежат 4 монеты, из которых одна сделана из другого металла и отличается по весу, хотя внешне они все одинаковые.
Как определить эту монету за 2 взвешивания на чашечных весах?
Ответ?
Варианты взвешиваний :
1) кладем на весы 1 и 2 монеты, если они равны по весу, то одну монету заменяем на третью.
Далее если они равны, то отличная монета 4-я, если не равны, то 3-я монета отличная от остальных.
2) кладем на весы 1 и 2 монеты, если они не равны по весу, то вместо одной монеты ложем 3-ю. Если уравновешиваются, то отличная убранная монета, если не уравновешиваются, то отличная от других монет оставшаяся на весах старая монета
#15
Как вы думаете, какой знак следует поставить между 0 и 1, чтобы было получено число больше 0, но меньше 1?
Ответ?
Этот знак является запятой. То есть 0,1. Это число больше 0, но меньше 1
#16
Как так могло оказаться, что половина числа 12 стало равно 7
Ответ?
Нужно написать число 12 римскими цифрами: IIX, далее провести посередине линию. Верхняя половина будет в виде VII, что соответствует цифре 7
#17
Трехлитровый сосуд полностью заполнен тремя литрами воды.
Вам необходимо за 2 переливания заполнить два пустых сосуда на 1 и 2 литра, чтобы в каждом из них было по 1 литру воды.
При этом больше нельзя пользоваться ничем, кроме этих трех сосудов.
Ответ?
Из полного сосуда наливаем в двухлитровый пустой ровно два литра, т.е. до краев.
Далее из этого сосуда выливаем в однолитровый ровно литр воды (т.е. до краев).
#18
На праздничном столе горят 7 свечей. 3 из них потушили. Сколько свечей останется?
Ответ?
Останутся 3 потушенные свечи, т.к. остальные 4 сгорят полностью.
#19
Как вы думаете, существуют ли линии отличные от окружности, на которых все точки будут равноудалены от какой-то одной точки?
Ответ?
Равноудаленностью всех точек обладает любая линя, лежащая на поверхности шара.
Логические задачи для 5, 6 класса
Задание 1.
Кот Матроскин и пес Шарик каждое утро бегают на речку умываться. Они выскакивают из дома одновременно и бегут по одной и той же тропинке. Скорость каждого из них постоянна, но Матроскин бежит в 3 раза быстрее Шарика, зато моется в 2 раза дольше, чем Шарик. Однажды Шарик, прибежав к речке, обнаружил, что не взял с собой полотенце. Он тут же побежал домой, схватил полотенце и прибежал к речке как раз в тот момент, когда Матроскин закончил умываться (бежал Шарик по той же тропинке и с той же скоростью, что и каждое утро).
Кто обычно прибегает домой раньше – Шарик или Матроскин или они прибегают домой одновременно?
Задание 2.
Известный бизнесмен Андрей Крутой пришел в Госбанк, чтобы обменять несколько 50- и 100- долларовых купюр старого образца.
Ему было выдано 1999 купюр достоинством 1, 5 и 25 долларов.
Докажите, что его обсчитали.
Задание 3.
Три землекопа за два часа выкопали три ямы.
Сколько ям выкопают шесть землекопов за пять часов?
Задание 4.
В Цветочном городе живет 14 коротышек. Они объединены в различные партии. По закону, партия должна состоять не менее чем из 3 коротышек, и две разные партии не могут состоять из одних и тех же членов. Кроме того, каждый коротышка может быть членом не более 2 партий.
Какое наибольшее число партий может быть в Цветочном городе?
Задание 5.
Во время шторма капитан корабля приказал выбросить за борт половину из 30 тюков с товарами, которые везли два купца. Купцы были в нерешительности: каждому было жаль выбрасывать свой груз. Видя это, капитан сказал: «Сделаем так: матросы расставят 30 тюков по кругу, а мы будем по кругу ходить и выбрасывать каждый девятый тюк, пока не выбросим половину тюков». Один из купцов подкупил матросов, и они сумели расставить тюки так, что 15 оставшихся на палубе тюков оказались с товарами одного купца.
Как были расставлены тюки?
Задание 6.
Футбольный мяч сшит из 32 лоскутков: белых шестиугольников и черных пятиугольников. Каждый черный лоскуток граничит только с белыми, а каждый белый — с тремя черными и тремя белыми. Сколько лоскутков белого цвета?
Задание 7.
Инженер ежедневно приезжал на станцию в одно и то же время, и в то же время за ним подъезжала машина, на которой он ехал на завод. Однажды инженер приехал на станцию на 55 мин раньше обычного. Сразу пошел навстречу машине и приехал на завод на 10 мин раньше, чем обычно.
Во сколько раз скорость инженера меньше скорости машины?
Задание 8.
В вагоне электропоезда ехали из города на дачу две подруги-школьницы.
«Я замечаю, – сказала одна из подруг, – что обратные дачные поезда нам встречаются через каждые 5 мин. Как ты думаешь, сколько дачных поездов прибывает в город в течение одного часа, если скорости поездов в обоих направлениях одинаковы?» «Конечно, 12, так как 60 : 5 = 12», – сказала вторая подруга. Но школьница, задавшая вопрос, не согласилась с решением подруги и привела ей свои соображения. А что вы думаете по этому поводу?
Задание 9.
В триседьмом царстве живут драконы. У каждого дракона одна, две или три головы,
а) Может ли у 40 % драконов быть 60 % голов?
б) Может ли у 40 % драконов быть 70 % голов?
Задание 10.
У филателиста Бори большое количество марок. Однажды он решил разместить их в большом альбоме, состоящем из 1000 страниц, так, чтобы на всех заполненных страницах марок было поровну (какие-то страницы в конце альбома могут остаться пустыми). Но когда Боря попробовал раскладывать по 7 марок на странице, то у него 5 марок осталось (но не все страницы были заполнены). Тогда он стал раскладывать сначала по 11 марок на странице, затем – по 13 марок на странице. Но снова у него оба раза осталось 5 марок. Наконец, когда Боря решил разложить по 23 марки на странице, то на этот раз у него осталось 6 марок.
Сколько марок в коллекции у Бори?
……………………………………………….
Решения логических задач для 5, 6 класса
Решение задачи 1.
Разделим дорогу от дома к речке на три участка одинаковой длины (см. рисунок) и эту длину примем за 1.
Введем новую единицу измерения – «шарик»; по определению, 1 «шарик» – это время, нужное Шарику, чтобы утром по дороге на речку пробежать участок длины 1.
По условию, когда Матроскин добегает до D (начинает умываться), Шарик как раз находится в точке B (ведь он бежит в 3 раза медленнее Матроскина). Следовательно, на дорогу от дома до речки (так же, как и на обратную дорогу) Матроскин затрачивает столько же времени, сколько нужно Шарику, чтобы пробежать отрезок длины 1, т. е. 1 «шарик».
Матроскин умывается 8 «шариков» (действительно, в тот день, когда Шарик забыл полотенце, он, как всегда, добежал до точки B, а Матроскин в этот момент начал умываться, затем Шарик пробежал 8 раз отрезок длины 1: от B к D (два участка длины 1), от D к A(три участка длины 1) и, наконец, от A к D уже с полотенцем (три участка длины 1), — и как раз Матроскин в этот момент умываться закончил). Далее, так как по условию Матроскин моется в два раза дольше Шарика, то Шарик моется 4 «шарика».
Остается подсчитать время, затраченное каждым из наших героев на дорогу от дома к речке, умывание и дорогу обратно, от речки к дому. Шарик: 3 + 4 + 3 = 10 «шариков»; Матроскин: 1 + 8 + 1 = 10 «шариков».
Следовательно, Матроскин и Шарик прибегают домой после умывания одновременно.
Решение задачи 2.
Для решения этой задачи необходимо воспользоваться следующим известным утверждением: сумма любого числа четных чисел – четная, а нечетного числа нечетных чисел – нечетная. В нашем случае исходная сумма денег (сумма какого-то числа 50-долларовых и 100-долларовых купюр) – четная, а полученная сумма денег (сумма 1999 купюр по 1, 5 и 25 долларов) – нечетная.
Решение задачи 3.
Шесть землекопов за 2 часа выкопают 3 · 2 = 6 ям. Шесть землекопов за 10 часов выкопают 6·5=30 ям. Тогда шесть землекопов за 5 часов выкопают 30 : 2 = 15 ям.
Решение задачи 4.
Пусть в каждой партии выдают партийные билеты. Если в цветочном городе k партий, то на руках у населения не менее 3k партийных билетов (ведь в каждой партии по условию не менее 3-х членов). Но у каждого коротышки имеется не более 2-х партийных билетов (по условию каждый коротышка не может быть членом более 2-х партий). Следовательно, так как коротышек 14, всего партийных билетов не более 2 x 14 = 28 .
Поэтому 3k Остается привести пример вхождения 14 коротышек в 9 партий такой, чтобы:
1) в каждой партии было не меньше 3 членов;
2) каждый коротышка являлся бы членом не более 2-х партий;
3) никакие две разные партии не состоят из одних и тех же членов (при выводе оценки k Пронумеруем коротышек числами от 1 до 14. Условимся коротышек, входящих в какую-либо партию, заключать в фигурные скобки {}. Нужный пример иллюстрируют, например, партии: {1,2,3}, {4,5,6}, {7,8,9}, {10,11,12}, {13,14,1}, {2,3,4}, {5,6,7}, {8,9,10}, {11,12,13}.
Всего 9 партий.
Решение задачи 5.
Начертим круг, отметим на нем 30 палочек и пронумеруем их от 1 до 30. Начиная счет с цифры 1, перечеркиваем девятую палочку, затем восемнадцатую, затем двадцать седьмую и продолжаем этот процесс, вычеркивая каждую девятую из не перечеркнутых ранее палочек. Таким образом, будут перечеркнуты палочки с номерами 5, 6, 7, 8, 9, 12, 16, 18, 19, 22, 23, 24, 26, 27, 30. Значит, купец просил матросов расставить тюки следующим образом: 4 своих, 5 чужих, 2 своих, 1 чужой, 3 своих, 1 чужой, 1 свой, 2 чужих, 2 своих, 3 чужих, 1 свой, 2 чужих, 2 своих, 1 чужой.
Решение задачи 6.
Обозначим искомое число лоскутков белого цвета через x. Тогда лоскутков черного цвета будет 32 — x. Чтобы составить уравнение, подсчитаем двумя способами количество границ белых лоскутков с черными. Каждый белый лоскут граничит с тремя черными, следовательно, число границ равно 3x. С другой стороны, каждый черный лоскут граничит с пятью белыми и число границ равно 5(32 – х). Получаем уравнение 3x = 5(32 – х), т.е. 8х = 160 и х = 20.
Решение задачи 7.
За 10 мин машина проходит путь, равный двойному расстоянию от станции до места встречи инженера с машиной. Значит, путь от станции до места встречи машина проходит за 5 мин. На месте встречи машина была за 5 мин до времени обычного приезда инженера на станцию, значит, путь от станции до места встречи инженер шел 55 мин — 5 мин = 50 мин. Следовательно, скорость инженера в 50 : 5 = 10 раз меньше скорости машины.
Решение задачи 8.
Скорости поездов одинаковы, поэтому за одно и тоже время они проходят одно и тоже расстояние. Из сказанного выше следует, что в город прибудут в течение одного часа только дачные поезда встречающиеся в первой половине часа (30 минут), а дачные поезда встречающиеся во второй половине часа не будут успевать доходить до города за оставшееся время.
Значит, в течение одного часа в город прибывает 30 : 5 = 6 дачных поездов.
Решение задачи 9.
а) Покажем, что у 40% драконов может быть 60% голов. Пусть в этом царстве живет 100 драконов: 40 драконов с одной головой, 20 – с двумя головами и 40 – с тремя. Тогда число голов у всех драконов равно 40 • 1 + 20 • 2 + 40 • 3 = 200. При этом все 40 трехглавых драконов, что составляет 40% от общего числа драконов, имеют 40 • 3 = 120 голов, что составляет 120/200 • 100% = 60% от общего числа голов.
б) Пусть число драконов равно х, а общее число голов у них равно у. Предположим, что какие-то 40% драконов имеют 70% голов. Тогда, поскольку каждый из этих драконов имеет не более трех голов, то 0,7у
Решение задачи 10.
Пусть у Бори х марок. Согласно условию х – 5 делится на 7, на 11 и на 13. Следовательно, поскольку 7,11 и 13 – простые числа, то х – 5 делится на их произведение, т. е. на 7 • 11 • 13 = 1001. Поэтому х – 5 = 1001k для некоторого натурального k, откуда х = 1001k + 5 .
Далее, согласно условию х – 6 делится на 23. Поэтому х – 6 = 23m для некоторого натурального m. В результате, получим
1001k – 1 = 23m. (*)
Остается только найти натуральные k и m, удовлетворяющие этому равенству. При этом, поскольку согласно условию х/7Поэтому находим единственное значение х = 1001•2 + 5 = 2007.
Задачи на логику с ответами 5 класс
6 класс