Урок-игра «Математические ребусы в картинках» (5-9 класс)
Математические ребусы в картинках
1)  показатель
показатель
Пояснение: ПО букве К расположена буква А, ЗА буквой Т стоит ЕЛЬ
2)  наклонная
наклонная
Пояснение: НА К стоит Л, ОН находится НА Я
3)  подобие
подобие
Пояснение: ПОД О находится БИЕ
4)  стереометрия
стереометрия
Пояснение: С, в слове ТЕРмОМЕТР заменяем первую М на Е, в слове ПЯть, убираем последние две цифры и П заменяем на И. Получается, стереометрия.
5)  теорема Пифагора
теорема Пифагора
Пояснение: Т, ОРЕЛ, МАК, ПИ, ФЛАГ, ОР, А.
В слове ОРЕЛ берем буквы по следующему порядку: 3, 1, 2, 3, получается ЕОРЕ. В слове МАК убираем последнюю букву К, получается МА. В слове ФЛАГ вычеркиваем букву Л, получается ФАГ. Соединяем Т, ЕОРЕ, МА, ФАГ, ОР, А, получается ТЕОРЕМА ПИФАГОРА.
6)  теорема
теорема
Пояснение: ТЕО, РАМА. В слове РАМА, заменяем первую букву А на Е. получается РЕМА. Соединяем ТЕО и РЕМА, получается ТЕОРЕМА.
7)  отрезок
отрезок
Пояснение: КОТ, РЕ, ЗОНТ. У слова КОТ, убираем первую букву, получается ОТ. РЕ оставляем без изменений. В слове ЗОНТ, заменяем НТ на К, получается ЗОК. Соединяем ОТ, РЕ, ЗОК, получается ОТРЕЗОК.
8)  задача
задача
Пояснение: ЗА и ДАЧА, получается ЗАДАЧА.
9)  минус
минус
Пояснение: нота МИ, НОС, у которого вторую букву заменяем на У, получается МИНУС
10)  число
число
Пояснение: ОЧКИ и СЛОН, в слове ОЧКИ зачеркиваем 1 и 3 буквы, в слове СЛОН убираем последнюю букву: ЧИ СЛО. Получается, ЧИСЛО.
11) 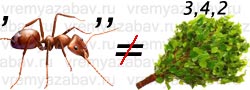 уравнение
уравнение
Пояснение: МУРАВЕЙ, НЕ и ВЕНИК. В МУРАВЕЙ убираем первую букву и две последних – УРАВ, в ВЕНИК берём 3, 4, 2 буквы – НИЕ. Значит: УРАВ НЕ НИЕ, получилось УРАВНЕНИЕ.
12)  ответ
ответ
Пояснение: КОТ в Е, КОТ. Убираем в слове КОТ первую букву – ОТ, находитя В Е, во втором слове КОТ убираем первые две буквы – Т. Значит, ОТ В Е Т. Получается, ОТВЕТ.
13)  пример
пример
Пояснение: ТРИ и РЕМЕНЬ. В ТРИ заменяем первую букву на П, получается ПРИ, в слове РЕМЕНЬ убираем последние 3 буквы и читаем полученное наоборот, получается МЕР. В ответе, получается ПРИМЕР.
14)  задача
задача
Пояснение: ЗА ДА находятся ЧАСЫ, у которых убираем последние две буквы. Получается, ЗАДАЧА.
15)  периметр
периметр
Пояснение: ПЕРО, МИ, РАКЕТА. У слова ПЕРо убираем последнюю букву, ноту МИ читаем наоборот, у слова ракета, берем буквы ЕТР, соединяем: ПЕР ИМ ЕТР. Получается, ПЕРИМЕТР.
16)  степень
степень
Пояснение: СТО, ПЕНЬ. В слове СТо заменяем О на Е, получилось СТЕ. Соединяем СТЕ и ПЕНЬ, получается СТЕПЕНЬ.
17)  знаменатель
знаменатель
Пояснение: З находится НА букве М; в слове ЕНОТ, заменяем О на А, получается ЕНАТ; ЕЛЬ. Соединяем З, НА, М, ЕНАТ, ЕЛЬ, получается ЗНАМЕНАТЕЛЬ.
18)  квадрат
квадрат
Пояснение: К букве В прибавляем справа А. У слова ДАРТС берем буквы под номерами 1, 3, 2, получается ДРА. У слова КИТ, убираем первые две буквы, получается Т. Соединяем К, В, А, ДРА, Т, получается КВАДРАТ.
Математические ребусы в картинках с ответами.
Разнообразить скучный урок помогут занимательные математические ребусы в картинках.
***
ребус 1
***
ребус 2
***
ребус 3
***
ребус 4
ребус 5
***
ребус 6
***
ребус 7
***
ребус 8
***
ребус 9
Простые математические ребусы в картинках с ответами — для детей и учителей математики.
А вот и ОТВЕТЫ на ребусы:
1. Алгебра
2. Геометрия
3. Линейка
4. Уравнение
5. Диаметр
6. Циркуль
7. Транспортир
8. Конус
9. Точка
Если у вас возникли сложности, прочитайте ЗДЕСЬ, как решать ребусы .
Еще математические ребусы вы сможете найти здесь — Математические ребусы. Ребусы с цифрами.
Математические ребусы
 Математика – одна из самых сложных наук, которая доставляет школьникам немало хлопот во время обучения. В то же время, навыки устного счета и различные математические приемы необходимо освоить каждому человеку, поскольку без этих знаний в современном мире жить просто невозможно.
Математика – одна из самых сложных наук, которая доставляет школьникам немало хлопот во время обучения. В то же время, навыки устного счета и различные математические приемы необходимо освоить каждому человеку, поскольку без этих знаний в современном мире жить просто невозможно.
Длительные и сложные уроки математики, особенно в младших классах, чрезмерно утомляют ребят и не позволяют им полноценно усваивать информацию. Чтобы такого не происходило, малышам необходимо подавать нужные сведения в форме веселой игры, например, в форме математических ребусов.
Подобные задачки могут быть разными по уровню сложности, поэтому начинать разгадывать их можно еще в детском саду. К тому же, ребусы практически всегда очень нравятся детям, и вам не придется заставлять свое чадо позаниматься. В данной статье мы расскажем вам, в чем польза математических ребусов для детей, и предложим несколько примеров для мальчиков и девочек разного возраста.
Что представляют собой математические ребусы и почему они так полезны для детей?
Математические ребусы – это загадки разных уровней сложности, которые составлены с использованием графических элементов. Разгадывание таких загадок является чрезвычайно увлекательным занятием, за которым можно провести не один час. Кроме того, ребята постарше с удовольствием составляют математические ребусы для своих одноклассников и друзей, и это тоже позволяет им тренировать интеллект и способствует развитию логического мышления.
В тех случаях, когда ребусы представляют собой довольно сложные загадки, мальчикам и девочкам приходится серьезно «поломать» голову, чтобы найти правильный ответ. В процессе этого увлекательного занятия у детей формируется нестандартное мышление. В дальнейшем этот навык пригодится для поиска возможных выходов из разных жизненных ситуаций.
Наконец, математические ребусы дарят ребятам заряд отличного настроения, а в том случае, если ребенок разгадывает их не один, а в компании друзей или родственников, — дополнительно способствуют социализации и укреплению отношений.
Примеры математических ребусов для дошкольников
Математические загадки для дошкольников должны быть самыми простыми. Обыкновенно они включают в себя 2-3 элемента, а их ответ представляет собой несложный математический термин или название цифры. В частности, для детей старшего дошкольного возраста подойдут следующие ребусы:
Математические ребусы для 1-4 класса
Ученики начальной школы уже хорошо знакомы с цифрами и некоторыми другими математическими терминами, поэтому они могут использовать их для составления и разгадывания различных ребусов. В этом возрасте чаще всего используются загадки, в тексте которых присутствуют цифры и другие аналогичные элементы. При этом ответ на такие ребусы может быть любым, в том числе, и не связанным с математической наукой.
В то же время, математические термины также могут быть зашифрованы в подобных задачках, но в этом случае они представляют собой достаточно сложные понятия, с которыми младшим школьникам еще только предстоит познакомиться. Следующие математические ребусы с ответами подойдут для учеников 1, 2, 3 и 4 класса:
Математические ребусы для учеников 5-9 класса с ответами
Для учеников средней школы, особенно 8-9 класса, ребусы по математике уже должны быть довольно сложными – такими, чтобы ребятам пришлось серьезно потрудиться, чтобы их расшифровать. В противном случае подобные задачки не смогут заинтересовать и надолго увлечь школьников, а значит, будут абсолютно бесполезны.
В частности, для занятий с учениками 6-7 класса и старше можно использовать такие математические ребусы с ответами, как:
Мастер класс для учащихся 5 классов по теме: «Решение математических ребусов»



Мастер класс для учащихся
5 классов по теме:
«Решение математических ребусов»
Подготовила:
Черемисина Любовь Владимировна,
учитель математики МБОУ «Троицкая СОШ №1»
с.Троицкое,
2013 год
Пояснительная записка
Пятиклассники активно откликаются на любые предложения учителя поучаствовать во внеклассном мероприятии, олимпиаде или конкурсе. Однако, как показывают результаты, навыков решения нестандартных задач у учащихся 5 классов нет.
Ко всему прочему, в настоящее время учителя испытывают нехватку современной методической литературы, предназначенной для работы со способными учащимися по организации и проведению кружковых занятий, олимпиад по математике.
Учителя осуществляют подготовку учащихся к олимпиадам, опираясь на свой собственный опыт, взгляды, работа ведется на эмпирическом уровне без должной теоретической основы.
Между тем обучение решению нестандартных задач на раннем этапе могло бы развивать математические способности, интерес к предмету у учащихся, гибкое, вариативное мышление ребенка. Меня заинтересовали наработки методического объединения преподавателей математики, физики и информатики ГОУ лицей №1524 г. Москва по подготовке одаренных учащихся 5 класса к олимпиадам по математике. Данный мастер класс можно использовать при проведении элективных курсов, кружковых занятий и на уроках математики.
Цель мастер класса- рассмотреть технологию организации работы учащихся с арифметическими ребусами.
При работе с такими типами заданий следует учитывать несколько технологичных приемов:
1. Следует предлагать детям обратные преобразования: сначала обычный пример сделать арифметическим ребусом, заменив цифры буквами; затем ребус превратить в обычный пример, разгадав числа. Тогда дети будут понимать, откуда берутся одинаковые цифры на месте одинаковых букв, лишний старший разряд, разная цифра в суммах одинаковых слагаемых и т.д.
2. Различные “секреты” ребусов не задавать одновременно, это следует делать поочередно, причем после введения каждого “секрета” и его подробного обсуждения предлагать детям самим придумать ребус с таким “секретом”.
3. Следует учитывать возрастные особенности детей: ребусы с буквами требуют умения учащихся абстрагироваться, выполнять в уме большую часть вычислительных операций.
4. Примеры со * решаются проще, чем ребусы с буквами. Они построены по принципу “распутай клубок”. Поэтому начинать работу следует именно с таких примеров.
Оборудование к мастер классу: компьютер, мультимедийный проектор.
Содержание
Историческая справка.
2.Арифметические ребусы со *.
3.Арифметические ребусы с буквами.
4. Литература.
Ход мастер класса
Краткая историческая справка.
Слово «ребус» происходит от латинского res (вещь) и обозначает представление имен, слов и фраз изображениями, фигурами, композициями из букв и т.п. Само слово появилось из латинской фразы «Non verbis sed rebus», что значит «Не словами, а при помощи вещей». Иногда термин rebus ассоциируют с латинским словом rebis: res (вещь, предмет), rebis (обращение).
Математические ребусы представляют собой примеры обычных арифметических действий (сложения, вычитания, деления и умножения), в которых часть или даже все цифры заменены на точки, звездочки, буквы или другие символы. Решить ребус — означает восстановить первоначальный вид математического равенства.
Существует несколько разновидностей математических ребусов. Например, в буквенных ребусах каждой буквой зашифрована одна определенная цифра. При этом одинаковые цифры шифруются одной и той же буквой, а разным цифрам соответствуют различные буквы. Математический буквенный ребус именуют криптарифмом, если в результате шифрования получилась какая-то осмысленная фраза. Например, УДАР+УДАР=ДРАКА
В математических ребусах зашифрованных иными значками, например звездочками, каждый символ может обозначать любую цифру от 0 до 9. Причём, некоторые цифры могут повторяться несколько раз, а другие не использоваться вовсе. Такие ребусы, зачастую, называют числовыми или цифровыми.
Математический ребус — довольно старая головоломка, изобретатель её не известен.
Первое упоминание об отечественных математических ребусах, автору проекта «Ребус № 1» удалось отыскать в книге выдающегося российского, советского учёного, популяризатора физики, математики и астрономии, одного из основоположников жанра научно-популярной литературы Якова Перельмана «Занимательная арифметика. Загадки и диковинки в мире чисел», выпущенной Ленинградским издательством «Время» в 1926 году (слайды 2-6)
2. Работа с арифметическими ребусами, где нужно заменить * недостающими цифрами и выполнить действие.
— Учитель предлагает внимательно рассмотреть примеры, записанные на доске, и найти «секрет» этих примеров.
3+ 5 = 8 8 – 2 = 6 6 + 4 = 10 10 – 7 = 3
-После того, как учащиеся выясняют, что результат каждого примера является началом следующего («цепочка» примеров), тогда учитель предлагает решить головоломку, которая называется «распутай клубок».
56 – Δ =
– 15 =
18 + 6 = Δ
+ 1 = ►
В ходе рассуждений, возникают вопросы: как решить примеры, в которых нет двух чисел? Почему задание называется «распутай клубок»?
В работе учащиеся выясняют, что один пример решить все таки можно. Таким образом, будет найдено значение Δ. Подставив его в первый пример, находим следующее число и т.д. Теперь детям понятно, почему назвали задание «распутай клубок».
Учитель предлагает детям последовательно решить следующие задания:
Распутать еще один «запутанный клубок
82 + = ►
+ 8 = Δ
Δ – 39 =
94 – 45 =
Превратить цепочку примеров в «запутанный клубок» (для этого некоторые цифры заменить геометрическими фигурами).
4 + 2 = 6 6 – 5 = 1 1 + 7 = 8 8 – 3 = 5
4 + 2 = Δ Δ – 5 = + 7 = – 3 = ►
Дети фиксируют основное правило: одинаковые цифры должны быть заменены одинаковыми значками (и наоборот).
3. Придумать самостоятельно «запутанный клубок». Для этого дети сначала должны составить цепочку примеров.
4. Вставить вместо Δ одну и ту же цифру, чтобы равенство было верным.
1Δ + 3Δ + 5Δ = 111
Дети выполняют это задание путем перебора вариантов:
1 + 1 + 1 = 3 не подходит; 2 + 2 + 2 = 6 не подходит
3 + 3 + 3 = 9 не подходит; 4 + 4 + 4 = 12 не подходит
5 + 5 + 5 = 15 не подходит; 6 + 6 + 6 = 18 не подходит
7 + 7 + 7 = 21 подходит — 21 + (10 + 30 + 50) = 111
Выполняя это задание, учащиеся, знакомятся с алгоритмом выполнения такого задания и формой записи: последовательный перебор возможных вариантов с фиксацией, подходит или нет такой вариант.
— Учитель предлагает детям следующее задание: Восстановить пример:
7 3 Δ 739
+2 6 +236
Δ 7 5 975
После выполнения задания обсудить, с чего начинали, чтобы распутать весь клубок. Выяснить, что, чтобы сложить многозначные числа, нужно сосчитать несколько примеров с однозначными числами, своеобразную цепочку. А такие задания мы выполнять умеем. Главное – найти подсказку, где «начинается клубок».
Совместно с учащимися, формулируем «секреты», которые помогают решать арифметические ребусы:
№1. Одинаковые знаки (буквы) обозначают одинаковые цифры.
№2. Чтобы решить такой пример, нужно найти начало «клубочка» (откуда будет раскручиваться логическое рассуждение).
№3. Нужно учитывать «переполнение» из соседнего разряда.
1
7 3 Δ
+ 2 6
Δ 7 5
Задания на закрепление:
1. Детям предлагается ряд примеров со *.
3 7 0 * * * 5 9 * _* 2 * 4 8 .
+ * 9 * 8 8 0 0 3 * * * *
9 * 4 0 5 0 8 * 2 * * * _ 2 *
* *
0
2. Запиши суммы обычными цифрами:
А А 0 А А В В В В К К 0 К К
+ А 0 А А А + В В В В + К К К К К
. . . 6 6 . . . 9 8 . . . . 5 4
Решая такие задания, дети выясняют еще два «секрета» арифметических ребусов, связанные с «переполнениями» из соседнего разряда:
откуда берется еще один разряд в сумме, и какая цифра там может быть? (только 1).
почему при сложении одинаковых знаков (букв) написаны (а значит, получаются) разные цифры? (виновато «переполнение» из соседнего разряда).
Открытия дополняют составленный ранее перечень «секретов»:
№4. На месте «свободного» старшего разряда в сумме может быть только цифра 1, которая получается из переполнения соседнего разряда.
№5. При сложении двух одинаковых букв могут получиться разные результаты. Виновато в этом «переполнение» из соседнего разряда.
нет переполнения 1 есть переполнение
Т Т Т Т
+ Т Т + Т Т
8 8 . 9 8
цифры одинаковые цифры разные
Значит, Т может быть равно 4, а может быть равно 9. Об этом обязательно следует помнить.
— Учитель предлагает детям решить следующие арифметические ребусы:
* * * + * = * * * * Ответ: 999+1=1000
* * * * * = * 100-99=1
* * * * * = * * * 1000-1=999
Дети сначала теряются, но потом быстро находят решение. Учитель спрашивает, почему была заминка? В чем (предположительно) ожидалась трудность? Учащиеся сообщают, что в этих ребусах нет ни одной известной цифры, только звездочки. Но смогли найти решение, потому что «секреты» арифметических ребусов, выведенные на предыдущем занятии, все равно работают.
Далее учитель предлагает детям несколько арифметических ребусов с буквами. Ребусы нужно решить и перечислить, какие «секреты» из уже известных использовались. Отдельно учитель предлагает фиксировать трудные моменты для поиска новых «секретов».
о х о х о
+ а х а х а
о х о х о х
Ответ: 1 0 1 0 1
+ 9 0 9 0 9
1 0 1 0 1 0 «Секреты» № 1,2, 3,4.
2) т р и
+ т р и
т р и
д ы р а
Ответ: 403
+ 403
403
1209 «Секреты» № 4, 2, 1.
Новый «секрет» №6 – если при сложении трех одинаковых цифр получается такая же, то это могут быть только цифры 0 или 5. Все зависит от того, нужно ли отсюда переполнение в более старший разряд.
г а
+ г о
у г у
Ответ: 9 5
+ 9 6
1 9 1 «Секреты» № 4, 2, 1.
Новые «секреты» :
№7: если при сложении двух одинаковых цифр получается такая же, то это могут быть только цифры 0.
№8: если же есть переполнение в этот разряд, то это может быть и цифра 9. Все зависит от того, нужно ли переполнение в более старший разряд. В данном ребусе не может ноль стоять в начале числа, значит, только 9.
Учитель предлагает детям буквенные ребусы на отработку всех известных «секретов». Обязательно обсуждать результат после нахождения решения: ввести форму записи «последовательности распутывания клубка».
к о ш к а 5 6 3 5 0
+ к о ш к а + 5 6 3 5 0
к о ш к а 5 6 3 5 0
с о б а к а 1 6 9 0 5 0
с – только1.
а + а + а = а только 0, так как из этого разряда не нужно переполнение.
к + к + к = к только 5.
к + к + к = о 5 + 5 + 5 (+ 1 из переполнения)= 6 – это о.
о + о + о = б 6 + 6 + 6 = либо 8 , либо 9.
Остаются цифры 2, 3, 4.
ш + ш + ш = 0 2 + 2 + 2 (+ 1 из переполнения) = 7 не подходит.
3 + 3 + 3 (+ 1 из переполнения) = 10 подходит, ш – 3.
Значит, если есть переполнение, то б – 9.
Домашнее задание: Решите ребусы:
ОДИН+ОДИН=МНОГО
РЕШИ+ЕСЛИ=СИЛЕН
ПОДАЙ-ВОДЫ=ПАША
СОТНЯ х 3 = ТРИСТА
Литература:
1.Система подготовки одаренных учащихся 5 класса к олимпиадам по математике. МО преподавателей математики, физики и информатики. ГОУ лицей №1524 г. Москва. http://do.gendocs.ru/docs/index-39863.html
2. http://rebus1.com/
Профессор Знаев — РЕБУСЫ К УРОКАМ МАТЕМАТИКИ
Ответы к ребусам.
1. Ромб
2. Стереометрия
3. Угол
4. Отрезок
5. Пифагор
6. Вектор
7. Минус
8. Лобачевский
9. Гаусс
10. Вершина
11. Диагональ
12. Доля
13. Дробь
14. Задача
15. Пирамида
16. Модуль
17. Аксиома
18. Конус
19. Точка
20. Задача
21. Транспортир
22. Равенство
23. Высота
24. Квадрат
25. Восемь
26. Знаменатель
27. Корень
28. Квадрат
29. Высота
30. Закон
31. Параллелепипед
32. Диаметр
33. Одиннадцать
34. Тринадцать
35. Показатель
36. Ордината
37. Брадис
38. Тупой угол
39. Циркуль
40. Апофема
41. Двенадцать
42. Пятнадцать
43. Пятнадцать
44. Медиана
45. Число
46. Следствие
47. Доказательство
48. Производная
49. Точка
50. Знаменатель
51. Каникулы
в картинках и текстовые, для взрослых и детей
«Безумный разрез» Мартина Гарднера
Мартин Гарднер — известный американский писатель, математик-любитель, автор множества статей и книг по занимательной математике, научно-популярных этюдов, математических фокусов, головоломок и задач на сообразительность и множества других публикаций.
Предлагаем решить одну из самых популярных головоломок Гарднера.

Сделайте один разрез (или нарисуйте одну линию) — не обязательно, прямую — чтобы разделить нарисованную фигуру на две одинаковые части.
Сингапурская головоломка
Благодаря социальным сетям некоторые головоломки распространяются, как вирус, и становятся известными. Так случилось с головоломкой, которую телеведущий Кеннет Конг из Сингапура разместил на своей странице в фейсбуке, и вскоре ею поделились 4400 человек.
Альфред и Бернард только что познакомились с Шерил и хотят выяснить, когда у нее день рождения.
Шерил показала поклонникам 10 возможных дат:

Затем она показала Альфреду месяц своего рождения, а Бернарду — день.
Чтобы решить головоломку, друзья обменялись парой реплик:
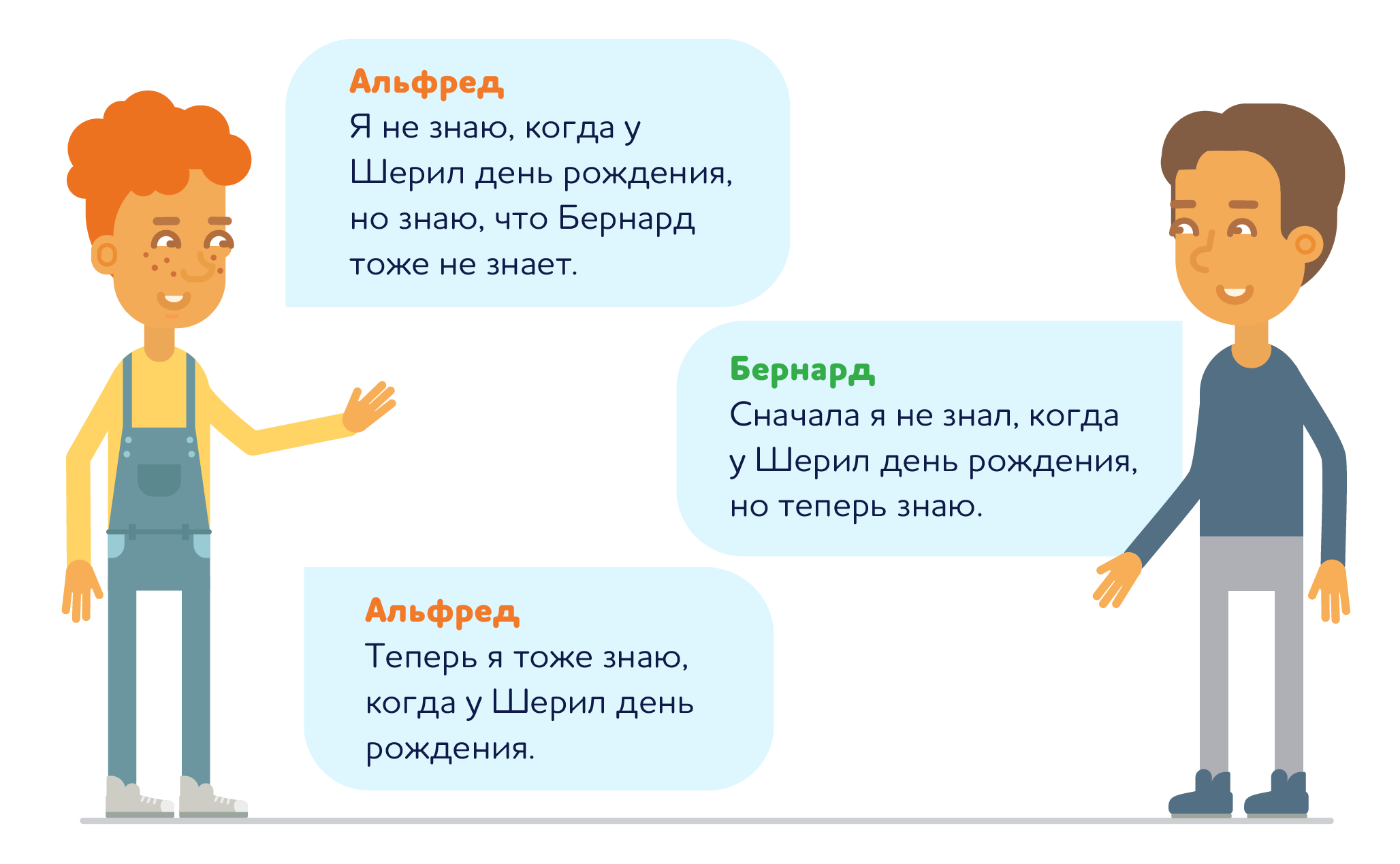
Так когда же у Шерил день рождения?
Танграм
Согласно легенде, головоломка была создана несколько тысяч лет назад тремя древнекитайскими мудрецами для сына императора. Правитель хотел чтобы через простую игру его сын постиг начала математики, научился видеть окружающий мир глазами художника, стал терпеливым, как философ, и осознал, что сложные вещи состоят из простых.
Так появился «Ши-Чао-Тю» — квадрат, разрезанный на семь частей:
5 треугольников (2 больших, 2 маленьких, 1 средний), квадрат и параллелограмм.
Суть «свободной» игры в танграм — собирать из имеющихся деталей по принципу мозаики всевозможные фигурки: животных, птиц, человека, что угодно. Младшим дошкольникам предлагают простой вариант развивающей игры, когда фигурки танграма нужно просто наложить на готовый образец-ответ.
Многие дети в 5-7 лет складывают модели из фигурок рядом с изображением-ответом, даже если размеры вырезанных фигур и деталей на картинке отличаются.
Танграм как головоломка обычно по силам ребенку начиная с 6-7 лет. Все так же — из элементов танграма нужно сложить готовую модель, но на карточке изображен лишь силуэт фигуры.
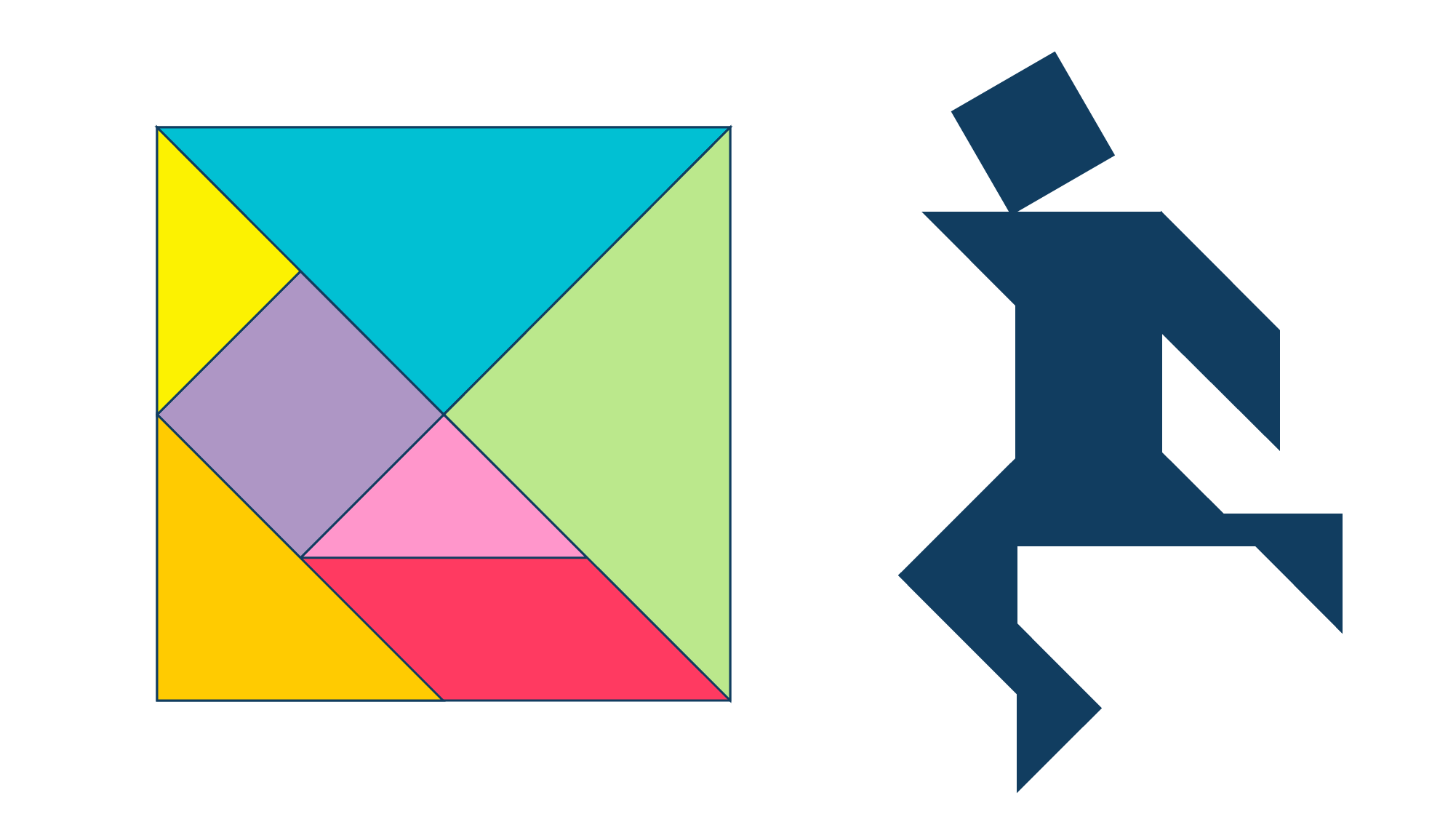
Вырежьте элементы танграма из бумажного, картонного или другого квадрата, и для начала предлагаем собрать одну из популярных фигурок — бегущего человека, как на рисунке выше.
Помните 2 правила головоломки:
1) необходимо использовать все 7 фигурок головоломки;
2) фигуры не должны накладываться друг на друга.
Среди поклонников танграма были Льюис Кэрролл и Наполеон Бонапарт. Считается, что именно «танграмом» назвал игру американский шахматист, изобретатель «пятнашек» и многих других головоломок, Самюэль Лойд.
В 21 веке самые интересные проявления танграма встречаются в дизайне мебели, одежды, ландшафтном дизайне и архитектуре.
Ребусы математические — IgraZa.ru. Игры, ребусы, загадки, викторины, кроссворды, головоломки, задачи
Савченко Елена Михайловна,
учитель математики
МОУ гимназия №1,
г. Полярные Зори, Мурманская область
Комплект математических ребусов разработан для дистанционного обучения детей решению загадок-ребусов. В архиве 59 ребусов-картинок, оформленных в едином стиле. Этот набор можно использовать для оформления математической газеты. Второй документ архива – это динамические модули в PowerPoint, на которых подробно показаны алгоритмы формирования слова по пикторгамме ребуса (в ней содержатся анимации для 25 ребусов из коллекции).
Разработаны обучающие интерактивные тестовые оболочки, которые вы можете увидеть на сайте http://le-savchen.ucoz.ru/board/8
Интерактивные оболочки работают не только в режиме online! Вы можете сохранить страницы на своем компьютере и использовать их в классе, где нет подключения к Интернету. Для этого надо раскрыть страницу с интерактивными ребусами, далее выбрать команду «сохранить как» и выбрать в меню команду «веб-страница, полностью».
Многие из предложенных ребусов являются авторскими.
Ответы к ребусам
- РОМБ
- СТЕРЕОМЕТРИЯ
- УГОЛ
- ОТРЕЗОК
- ПИФАГОР
- ВЕКТОР
- МИНУС
- ЛОБАЧЕВСКИЙ
- ГАУСС
- ВЕРШИНА
- ДИАГОНАЛЬ
- ДОЛЯ
- ДРОБЬ
- ЗАДАЧА
- ПИРАМИДА
- МОДУЛЬ
- АКСИОМА
- КОНУС
- ТОЧКА
- ЗАДАЧА
- ТРАНСПОРТИР
- РАВЕНСТВО
- ВЫСОТА
- КВАДРАТ
- ВОСЕМЬ
- ЗНАМЕНАТЕЛЬ
- КОРЕНЬ
- КВАДРАТ
- ВЫСОТА
- ЗАКОН
- ПАРАЛЛЕЛЕПИПЕД
- ДИАМЕТР
- ОДИНАДЦАТЬ
- ТРИНАДЦАТЬ
- ПОКАЗАТЕЛЬ
- ОРДИНАТА
- БРАДИС
- ТУПОЙ УГОЛ
- ЦИРКУЛЬ
- АПОФЕМА
- ДВЕНАДЦАТЬ
- ПЯТНАДЦАТЬ
- ПЯТНАДЦАТЬ
- МЕДИАНА
- ЧИСЛО
- СЛЕДСТВИЕ
- ДОКАЗАТЕЛЬСТВО
- ПРОИЗВОДНАЯ
- ТОЧКА
- ЗНАМЕНАТЕЛЬ
- КАНИКУЛЫ
Математики
- БУЛЬ
- ФЕРМА
- ВИЕТ
- БУЛЬ
- ДЕКАРТ
- ВЕЙЕРШТРАСС
- ЧЕБЫШЕВ
- ОСТРОГРАДСКИЙ
Скачать архив объемом 5,89 Мб из 59 ребусов-картинок, оформленных в едином стиле. Этот набор можно использовать для оформления математической газеты. Второй документ архива – это динамические модули в PowerPoint, на которых подробно показаны алгоритмы формирования слова по пикторгамме ребуса (в ней содержатся анимации для 25 ребусов из коллекции)
 показатель
показатель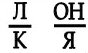 наклонная
наклонная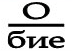 подобие
подобие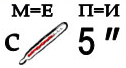 стереометрия
стереометрия теорема Пифагора
теорема Пифагора теорема
теорема отрезок
отрезок задача
задача