Математика 5 класс правила и формулы: Основные правила математики. 5 класс – Правила по математике 5-6 классы — Молитва

Содержание

Основные правила математики. 5 класс

Содержание

Натуральные числа
Сравнение натуральных чисел
Свойства сложения
Формула пути
Корень уравнения
Правила решения уравнений
Отрезок, прямая, луч
Угол, биссектриса угла
Углы: развернутый, прямой, острый, тупой
Многоугольники. Равные фигуры
Треугольники: остроугольный, прямоугольный, тупоугольный
Треугольники: равнобедренный, равносторонний, разносторонний
Прямоугольник. Квадрат. Периметр
Умножение. Свойства умножения
Деление. Деление с остатком
Площадь. Площадь квадрата, прямоугольника
Объем. Объем прямоугольного параллелепипеда, куба
Дроби: правильная, неправильная, сравнение дробей
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Преобразование неправильной дроби в смешанное число
Преобразование смешанного числа в неправильную дробь
Десятичные дроби: свойства, сравнение, округление
Десятичные дроби: сложение, вычитание
Десятичные дроби: умножение, деление
Среднее арифметическое
Процент

Натуральные числа

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число меньше любого натурального числа.
Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.
Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр.

Свойства сложения

Переместительный закон:

Сочетательный закон:

Формула пути

S = Vt ,
где — пройденный путь, — скорость движения, — время, за которое пройден путь .

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

Что значит “Решить уравнение”

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, надо делитель умножить на частное.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Отрезок, прямая, луч

Отрезок

Отрезок – часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

Луч

Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

Угол, биссектриса угла

Угол

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

Свойство величины угла

Если между сторонами угла ABC провести луч , то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC , то есть .

Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Углы: развернутый, прямой, острый, тупой

Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.

Многоугольники. Равные фигуры

Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный

Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.

Треугольники: равнобедренный, равносторонний, разносторонний

Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле P=3a

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.

Прямоугольник. Квадрат. Периметр

Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна , то его периметр вычисляют по формуле P=4a .

Умножение. Свойства умножения

Умножение

Свойства умножения

Переместительный закон умножения: $a \cdot b = b \cdot a$
Сочетательный закон умножения: $(a \cdot b )c= a( b \cdot c)$
Распределительное свойство умножения относительно сложения:
Распределительное свойство умножения относительно вычитания:

Деление. Деление с остатком

Деление

Для натуральных чисел a, b, c равенство $a \div b = c$ является правильным, если является правильным равенство

$b \cdot c = a$

В равенстве $a \div b = c$ число называют делимым, число — делителем, число и запись $a \div b$ – частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа правильными являются равенства:

$0 \div a = 0$ ,

$a \div a = 1$

Деление с остатком

a=bq+r , где — делимое, — делитель, — неполное частное, — остаток, r < b .

Если остаток равен нулю, то говорят, что число делится нацело на число .

Площадь. Площадь квадрата, прямоугольника

Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

где — площадь квадрата, — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба

Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда

где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;

где — площадь основания параллелепипеда, — его высота.

Объем куба

где — объем куба, — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей

Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.
Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.
Все правильные дроби меньше единицы, а неправильные — больше или равны единице.
Любая неправильная дробь больше любой правильной дроби.

Сложение и вычитание дробей с одинаковыми знаменателями

Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.

Сложение и вычитание смешанных чисел

Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.
Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

числитель разделить на знаменатель;
полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

целую часть числа умножить на знаменатель дробной части;
к полученному произведению прибавить числитель дробной части;
эту сумму записать как числитель неправильной дроби;
в его знаменателе записать знаменатель дробной части смешанного числа.

Десятичные дроби: свойства, сравнение, округление

Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
после чего сравнить полученные дроби поразрядно.

Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

все следующие за этим разрядом цифры отбросить.
если при этом первая из цифр, которые отбрасывают равна 0, 1, 2, или 4, то последнюю из цифр, которые оставляют, не меняют;
если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8 или 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.

Десятичные дроби: сложение, вычитание

Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

уравнять количество цифр после запятых;
записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
сложить полученные числа так, как складывают натуральные числа;
поставить в полученной сумме запятую под запятыми.

Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

уравнять количество цифр после запятых;
записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
выполнить вычитание так, как вычитают натуральные числа;
поставить в полученной разности запятую под запятыми.

Десятичные дроби: умножение, деление

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

перемножить их как натуральные числа, не обращая внимания на запятые;
в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
выполнить деление на натуральное число.

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Процент

Процентом называют сотую часть величины или числа 1%= $\frac{1}{{100}}$

Данная информация взята из УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир

Все главные формулы по математике — Математика — Теория, тесты, формулы и задачи

Формулы сокращенного умножения

К оглавлению…

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:

Квадратное уравнение и формула разложения квадратного трехчлена на множители

К оглавлению…

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

Парабола

График параболы задается квадратичной функцией:

При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:

Игрек вершины параболы:

Свойства степеней и корней

К оглавлению…

Основные свойства степеней:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:

Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

Формулы с логарифмами

К оглавлению…

Определение логарифма:

Определение логарифма можно записать и другим способом:

Свойства логарифмов:

Логарифм произведения:

Логарифм дроби:

Вынесение степени за знак логарифма:

Другие полезные свойства логарифмов:

Арифметическая прогрессия

К оглавлению…

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

Геометрическая прогрессия

К оглавлению…

Формулы n-го члена геометрической прогрессии:

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Тригонометрия

К оглавлению…

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Формулы двойного угла

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Тригонометрические формулы преобразования произведения в сумму

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формулы половинного угла

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы:

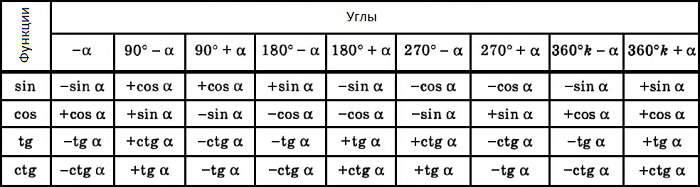
Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения

К оглавлению…

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений в некоторых частных случаях:

Геометрия на плоскости (планиметрия)

К оглавлению…

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы:

Свойство биссектрисы:

Формулы биссектрисы:

Основное свойство высот треугольника:

Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

Геометрия в пространстве (стереометрия)

К оглавлению…

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

Координаты

К оглавлению…

Длина отрезка на координатной оси:

Длина отрезка на координатной плоскости:

Длина отрезка в трёхмерной системе координат:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):

Таблица умножения

К оглавлению…

Таблица квадратов двухзначных чисел

К оглавлению…

Расширенная PDF версия документа «Все главные формулы по школьной математике»:

К оглавлению…

План-конспект урока по алгебре на тему: Урок по математике в 5 классе по теме «Формулы»

Разработка урока математики в 5 классе по теме:

«Формулы. Решение задач на движение с помощью формул »

(по учебнику Н.Я.Виленкин, В.И.Жохов и др.)

Разработка урока математики в 5 классе по теме

«Формулы. Решение задач на движение с помощью формул »

(по учебнику Н.Я.Виленкин, В.И.Жохов и др.)

Тема урока: Формулы. Решение задач на движение с помощью формул.

Класс: 5 класс.

Предмет: математика.

Задачи:

— познакомить учащихся с понятием «формула»; учить выполнять вычисления по формулам;

— продолжить формирование навыков решения текстовых задач;

— развивать память, навыки самоконтроля; умение выполнять анализ, делать выводы;

— воспитывать добросовестное отношение к учению, активность, аккуратность;

— повышать устойчивый интерес к способам решения познавательных задач.

Оборудование : тетради, доска, магнитная доска, проектор, раздаточный материал.

Формирование УУД:

Познавательные: ставить цели, отвечать на вопросы, применять уже изученный материал, работа с текстом задач
Регулятивные: постановка личных целей, технология оценивания, действия по плану
Коммуникативные: работа в парах, оценивание своих результатов.

Ход урока:

(синим цветом указаны действия учащихся и их предполагаемые ответы)

1.Организационный момент.

Здравствуйте, ребята!

Вот звенит для нас звонок –

Начинается урок.

Ровно встали, подтянулись

И друг другу улыбнулись!

Тихо садимся за парты и настраиваемся на урок. (Слайд №1.)

Весь необходимый раздаточный материал находится у вас на столах. Записываем в своих тетрадях: дата, классная работа.

2.Мотивация к деятельности.

Великими людьми оставлено нам в наследство множество различных высказываний, которые мы цитируем в тех или иных ситуациях. Сегодня я хочу предложить вашему вниманию слова древнего китайского мыслителя Конфуция, который говорил: (Слайд №2)

Три пути ведут к знаниям;

Путь размышлений- самый благородный,

Путь подражания- самый легкий,

Путь опыта- самый горький.

— А какой путь или несколько путей выбираете вы, ребята?

(Путь размышлений, путь опыта)

— Как вы думаете, чем вы будете заниматься сегодня на уроке?

(- Размышлять, набираться опыта.)

— Скажите, а для чего вам нужен какой-либо опыт?

(Приобретённый опыт поможет в дальнейшем в решении жизненных ситуаций.)

— И так, вы выбрали свой путь к знаниям.

У каждого из вас на столах есть «Путевой лист», в котором вы самостоятельно будете отмечать свои достижения на протяжении всего урока.

-Посмотрите внимательно на «путевой лист».Что он в себя включает?

(- В листе дан маршрут, путь к знаниям, в виде таблицы. В таблице показаны задания, за выполнение которых мы ставим себе оценки.)

— Вы совершенно правы. Иными словами можно сказать, путевой лист содержит для ваших учебных действий что ??? (пауза-вопрос) .

(- План действий.)

— Что вы будете делать сегодня на уроке для пополнения своего опыта?

— (дети зачитывают из путевого листа) Выполнять математический диктант; решать задачи; решать логическую задачу; выполнять задание на знание единиц измерения; отвечать на тест.)

3.Актуализация знаний.

-Выполним математический диктант.

-Я зачитываю выражения, а вы в своих тетрадях записываете их средствами математического языка (с помощью знаков, чисел, букв).

Диктант:

— произведение числа 245 и в

— частное чисел 393 и 3

— произведение суммы чисел 15 и 45 и числа с

— произведение числа а и разности 129 и 19

— произведение чисел m и n равно 15

— для того, чтобы найти скорость, нужно расстояние разделить на время.

-Обменяйтесь тетрадями друг с другом, проверьте, занесите свои первые достижения в путевой лист. (Слайд №3)

(Эталон оценивания: каждое выражение-1б.

5б-оценка «5»;4б- оценка «4»; 3б-оценка «3», 2б- оценка «2»)

(Дети обмениваются тетрадями, взаимопроверка.)

4.Постановка учебной задачи.

-Все ли выражения диктанта вы смогли написать средствами математического языка?

(- Нет, не смогли записать последнее выражение.)

-Почему возникли затруднения? Что еще вы не знаете?

(-Не знаем, как записать слова «скорость», «расстояние», «время» с помощь математических символов.)

— Ребята, а что это за выражение, которое вы не смогли записать символами?

(- Это правило для нахождения скорости.)

— Где вы можете применить это правило?

(- При решении задач на движение.)

— Как вы думаете, какова тема нашего урока?

(- Решение задач на движение по правилам, записанным в виде математических символов.)

5. «Открытие» нового знания.

— У вас на столах есть листок с задачами. Работаем парами. Внимательно посмотрите на задачи. Разделите их на две группы. Обоснуйте, по каким признакам делили?

(Учитель должен подвести к правильному разделению:

1 группа — №1,№3, №4

2 группа — №2,№5) (Слайд№4)

Беседа (на протяжении беседы демонстрируется Слайд №5, ответы учеников появляются в проецируемом изображении по клику «мыши»)

— О каких величинах идёт речь в этих задачах?

(- Скорость, время, расстояние.)

— Каковы правила для нахождения этих величин?

(- Дети произносят правила.)

-Такие записи длинные?

(- Да.)

— Как вы думаете, есть ли особое обозначение этих величин в математическом языке?

(- Скорее всего, есть.)

— Ваше предположение верное. Действительно, эти величины принято обозначать буквами латинского алфавита: S,V,t.

— А теперь возможно ли записать правило из нашего диктанта средствами математического языка? Как это будет выглядеть?

(V= S : t )

-А правила для нахождения расстояния и времени как можно

записать?

(t= S : V

S= V ∙ t )

— Такая запись называется ФОРМУЛОЙ.

— Так что же такое – ФОРМУЛА?(Слайд №6)

(- Дети сами формулируют определение: Формула – запись какого-нибудь правила с помощью букв.) (Слайд №7)

— В начале урока вы сформулировали тему урока следующим образом:

« Решение задач на движение по правилам, записанным в виде математических символов.»

Не поменялось ли ваше мнение сейчас? Как более точно можно сформулировать тему урока?

(- Тему можно сформулировать так: Решение задач на движение с помощью формул.) (Слайд №8)

— Верно. Запишите тему урока в своих тетрадях.

— Какие цели вы поставите для себя на этом уроке?

(- вспомнить, как решаются задачи на движение; научиться правильно применять формулы при решении задач.)

— Запишите в тетради формулы, которые вы будете использовать при решении задач.

(ученики записывают в тетрадях, а учитель крепит формулы на магнитной доске в классе.) (Слайд №9)

6.Первичное закрепление.

-Вернемся к задачам, которые вы разделили на группы. Решим задачи первой группы. Работать будем снова в парах.

Чтобы сократить время на запись решения каждой задачи, предлагаю составить единую таблицу для решения этих задач.

— Сколько задач в группе? Где расположим в таблице?

(Три, это будут строки.)

— О каких величинах идет речь? Где расположим в таблице?

(- V,t, S. Это – столбцы.)

— Формулы вам необходимы? Где расположим?

(- Это будет ещё одна строчка.)

— Найдите таблицы в раздаточном материале. Заполните таблицу известными данными из задач и найдите неизвестные. (Слайд №10)

— Прежде, чем приступить к решению задач, давайте напомним алгоритм( или план) решения задач.

(- Алгоритм:

1.Внимательно читаем задачу.

2.Составляем краткую запись, схему или таблицу.

3.Подбираем формулу.

4.Правильно решаем задачу.) (Слайд№11)

— Молодцы, алгоритм знаете. Теперь смело приступайте к решению задач и заполнению таблицы.

(Дети решают задачи, заполняют таблицу)

— Готовы? Проверьте правильность выполнения задания по эталону. Не забывайте отмечать свои достижения в путевом листе.

— (Дети сверяют таблицу со слайдом.) (Слайд №12)

7.Физминутка.

(гимнастика для глаз по тренажеру Базарного.) (Слайд №13)

-Совсем недавно в нашей стране в городе Сочи проходили гонки «Формулы 1».Вы уже, наверное, отметили, что решаемые сегодня задачи посвящены именно этой теме. А сейчас я предлагаю на короткое время представить себе, что Вы в Сочи находитесь на трибунах трассы гонок, и поболеть немного за болидов (так называют машины «Формулы1»).

Далее детям предлагаются вариации эмитации движения машин по тренажёру Базарного (по трассе), за которыми они следят только глазами.

8.Домашнее задание. (Слайд №14)

-Прежде, чем вы продолжите работу, запишите домашнее задание.

Базовый уровень –с.103(читать, учить правила),№ 701, №675, №696;

Повышенный уровень — с.103(читать, учить правила),№ 683, №735(1).

9.Включение в систему знаний и повторение.

-Вернемся к задачам второй группы. Выберите для решения ту задачу, с которой вы можете справиться.

(Два ученика решают выбранную ими задачу у доски, остальные самостоятельно в тетради)

— Проверим, как вы справились с заданием. (Заслушиваются решения ребят, работавших у доски. Остальные по их решениям проверяют свои. Оценивают себя в путевом листе.)

10.Работа с одарёнными детьми. (Слайд №15)

(решение «провоцирующей» задачи на выявление критичности мышления учащихся.)

11.Повторение.

— Молодцы. Как много в классе тех, кто догадался, как решить логическую задачу. А сейчас задание для всех.

-У вас на столах в раздаточном материале есть лист с заданием на знание единиц измерения. Если вы правильно выполните задание и заполните таблицу ответов, то сможете прочесть некое слово. (Слайд №16)

(Дети выполняют задание.)

— Проверим, какое же слово у вас получилось? (Слайд №17)

— Светофор.

— Отметьте свои достижения в путевом листе.

12.Рефлексия деятельности. (Итог урока.)

— На автомобильных дорогах движение регулирует светофор. И все знают, что означают его цвета. У вас на партах есть сигнальные листы таких же цветов, что и у светофора:

«Зелёный» – я всё понял

«Желтый» — остались вопросы

«Красный» — есть большие затруднения.(Слайд № 18)

Просигнализируйте, как вы поняли тему урока?

— На сигнальных листах, которые у вас сейчас в руках, тесты для выяснения степени понимания вами темы урока. Выполните задания тестов. (тесты разноуровневые: красный – базовый уровень, зеленый и желтый – повышенный. )

— Проверьте правильность выполнения заданий тестов.(Слайд №19).

— Отметьте свои достижения в путевом листе, поставьте итоговую оценку.

(Дети проверяют правильность выполнения заданий теста, выводят итоговую оценку в путевом листе)

— И так, ребята, наш урок подходит к концу.

— Скажите, что нового вы открыли для себя на уроке?

— Чему научились?

— Какую цель ставили?

— Удалось достичь этих целей?

— Что на уроке получалась?

— Над чем ещё надо поработать?

-Вы сегодня хорошо потрудились. Сдайте свои путевые листы. Если вас заинтересовало решение задач на движение, дома можете выполнить любые задания из листа «Дополнительные задачи».Это задание необязательное, но не останется без оценки при выполнении.

Урок окончен. До свидания. (Слайд №20.)

Использованное ресурсное обеспечение:

1.Федеральный государственный образовательный стандарт основного общего образования, утвержденный приказом Министерства образования и науки РФ от 17 декабря 2010 года № 1897.

2.Примерная программа по учебным предметам по математике. М.: Просвещение, 2011г.

3.Учебник «Математика 5» Н.Я.Виленкин, В.И.Жохов и др. / В.И.Жохов, М.: Мнемозина, 2010

4.Концепция математического образования РФ.

5.Я иду на урок математики.5класс:Книга для учителя.-М.: Издательство «Первое сентября», 2000.

6.Контрольно – измерительные материалы.Математика.5 класс/Сост.Л.П.Попова.-3-у изд., перераб.-М.:ВАКО,2014.

7.Интернет – ресурсы:

— sochiautodrom.ru/,официальный сайт «Формулы1»в Сочи

— Уроки математики, сайт учителя Соколовой А.А

— nsportal.ru, Социальная сеть работников образования «Наша сеть»

— рedsovet.su, сообщество взаимопомощи учителей.

План-конспект урока по математике (5 класс) по теме: Урок математики в 5 классе по теме «Формулы»

Ход урока

Организационный этап

Ребята, послушайте, какая тишина!

Это в школе начались уроки,

Мы не будем тратить время зря

И приступим все к работе.

Формулирование темы и цели урока

1Слайд

Ребята, вы назовёте тему нашего урока, если правильно решите ребус.

Итак, тема урока «Формулы»

Формул в математике очень много, а сегодня мы с вами рассмотрим лишь несколько.

2Слайд

-формулы пути, площади и периметра.

Попробуйте исходя из темы урока, поставить для себя цель на урок, а я вам помогу…

3Слайд

Продолжите вопрос

Итак, вперёд, к достижению цели!

4Слайд

Жила-была загадочная королева Формула.Она была непоседа и постоянно путешествовала из государства Алгебра в государство Геометрия. Она имела множество имён и так часто менялась, что подданные не узнавали её в лицо. То она Формула Пути, то Формула для Вычисления Площади Прямоугольника.Она очень добра и всегда готова помочь тому,кто не только узнаёт её с первого взгляда, но и знает наизусть все её имена. Потому что ФОРМУЛА – это…

Давайте разберёмся

Актуализация знаний

5Слайд

Узнали сказочных героев?, они предлагают вам вопрос: (работа по слайду фронтально с классом, отвечают устно)

Начертите прямоугольник, обозначьте его стороны. Какой буквой обозначается площадь в математике?…

Формула – это правило, а правила обязательно надо знать. Поэтому каждую формулу запишите в тетрадь и запомните, т.к принцесса Формула добра только с теми, кто сразу её узнаёт.

Чтобы сразу её видеть, поставьте на поля знак!

(Учитель на доске, ребята в тетрадях)

Изучение нового материала

6Слайд

Итак, мы познакомились пока с тремя её именами, какими?

7Слайд

Подскажите Страшиле формулу пути. Как из этой формулы узнать скорость? (Назовите компоненты в произведении. Как найти неизвестн. множитель)

Запишите в тетрадь и запомните

Как узнать время?

Запишите в тетрадь и запомните

Сейчас я предлагаю поработать самостоятельно, постарайтесь заполнить пустые ячейки таблицы. Считаем устно, ответы заносим в таблицу(3 мин). Обратите внимание: указаны единицы измерения величин и вы в ответе указывайте их тоже.

Готовы к проверке? Возьмите простые карандаши, если ваш ответ совпадает с ответом на экране, обведите его в кружок. (Разобрать последнее задание)

А сейчас оцените свою работу: посчитайте количество обведённых ответов, поставьте на поля оценку: сколько обведённых ответов, такая и оценка.

Формула пути помогает в решении текстовых задач. Давайте в этом убедимся.

8Слайд

Я приглашаю к доске…

Прочитай задачу

Часто при решении задач на движение выполняют схематический рисунок,

Сама на доске, дети в тетрадях

Кто желает решить задачу по рисунку?

-Какие величины известны?

-Что нужно найти?

-Напиши формулу пути

-На сколько километров каждый час поезда будут удаляться друг от друга?

-эта величина будет называться скоростью удаления поездов.

-найди скорость удаления поездов.

-Подставь известные числа в формулу

Выпиши ответ.

Пояснение в решении задачи писать не нужно, т.к. в формуле видно какую величину мы нашли.

9Слайд

А сейчас я предлагаю вам поработать в парах: посоветоваться друг с другом и записать формулы для нахождения площади и периметра квадрата.(1 мин)

Проверим ваши формулы.

Поднимите руку, у кого в тетради также.

Вот и ещё два новых имени у принцессы Формула мы нашли, их нужно тоже запомнить.

10 слайд

Страшила не может найти что?(дети — периметр и площадь квадрата),

Давайте ему поможем, выполните задание в тетради, если сомневаетесь, можно посоветоваться в парах

11Слайд

Устный счет + физкультминутка

Отдохнём сейчас не в шутку, проведём Физкультминутку. Все встаньте. Страшила решил задания, а вы сейчас их проверьте: на каждый правильный ответ задания вы должны поднять руки вверх и похлопать в ладоши, на неправильный – покачать головой влево и вправо.

Закрепление нового материала

12 слайд

Итак, какие формулы мы сегодня изучили? Назовите их. Давайте их сосчитаем(ответы уч-ся) (7).

Пути

Времени

скорости

Площадь прямоуг

Периметр прямоуг

Площадь квадр.

Периметр квадр.

Как я говорила, Принцесса Формула любит путешествовать и сейчас я вам предлагаю отправиться вместе с ней в путь к успеху, Для этого вам нужно подняться на 2 ступени.

Вы поднимитесь на 1 ступень если выполните верно 6 тестовых заданий на ПК

Чтобы подняться на 2 ступень надо решить №680

Когда вы выполните все задания, вы должны поднять руку и я помогу вам в проверке.

Подведение итогов урока:

Время выполнения самостоятельной работы подходит к концу, давайте подведём итоги.

-посмотрите на свои оценки на полях и скажите мне какую общую оценку за работу на уроке вы бы себе поставили (подхожу к каждому, комментирую)

-кто доволен своей оценкой может поставить её в дневник, а кто не доволен, то я вам даю возможность дома ещё поработать и на следующем уроке её повысить.

13 слайд

Рефлексия

Каждый из вас шёл по пути к Успеху, кто считает, что он сегодня на уроке достиг успеха и доволен своей работой?

У вас на столе фигуры.

Если вы считаете…

Я хорошо понял, как по формуле вычислить расстояние, скорость, время, площадь и периметр.
Я не все понял, у меня были ошибки.
Я не понял, как вычислять по формуле расстояние, скорость, время, площадь и периметр.

14 слайд

А сейчас домашнее задание, как выдумаете самое важное, с чего нужно начать выполнение д/з: выучить формулы,

№681(задача на движение)

+ задание на карточке

«Формулы» (математика 5 класс)

Конспект урока в 5 классе по теме «ФОРМУЛЫ»

Цели урока:

Систематизировать знания о нахождении неизвестного.

Ввести понятие формулы.

Выяснить особенности решения задач с помощью формул .

Продолжить развитие способностей учащихся к анализу и синтезу изучаемого материала, умения выделять главное и приводить соответствующие примеры, воспитывать волю и настойчивость при решении систем уравнений, показать возможность применения на уроке математики знаний, полученных на уроках по информационным технологиям, прививать интерес учащихся к предмету.

Ход урока:

1.Организационный момент.

Здравствуйте ребята, садитесь. Сегодня у нас необычный урок, мы отправимся в путешествие, а помогут нам в этом – компьютеры, мультимедийный проектор, интерактивная доска. А вот в какую страну мы отправимся, вам придётся отгадать. Так как у нас урок математики, вы будите выполнять задания и отгадывать буквы, из которых состоит слово.

2. Устная работа:

Итак, 1 задание (пишу ответ) – мы отгадали первую букву «Я», хорошо, а ты получаешь поощрительную картинку.

2 задание (пишу ответ) – мы отгадали вторую букву «П», хорошо, а ты получаешь поощрительную картинку.

3 задание (пишу ответ) – мы отгадали третью букву «О», хорошо, а ты получаешь поощрительную картинку.

4 задание (пишу ответ) – мы отгадали четвертую букву «Н», хорошо, а ты получаешь поощрительную картинку.

5 задание (пишу ответ) – мы отгадали пятую букву «И», хорошо, а ты получаешь поощрительную картинку.

Для выполнения следующего задания откройте учебник на странице 105 №5 задание (пишу ответ) — мы отгадали 6 букву «Я», хорошо, а ты получаешь поощрительную картинку.

Как же называется страна, в которую мы отправляемся? Верно Япония.

Для того чтобы отправиться в путешествие нам нужно выбрать маршрут, вид транспорта. Узнать расстояние, рассчитать время.

3.Объяснение нового материала

Для подготовки к путешествию нам поможет новая тема (Формула пути).

Ребята, давайте разберем задачу.

Что известно в задаче? (что ещё)
Что нужно найти?
Кто из вас уже решил задачу?
Давайте проверим.

Задачи на нахождение расстояния, скорости и времени решают с помощью формулы нахождения пути.

Читаю «Обозначим путь…..» — запишите в тетрадь.

Решим следующую задачу – прочитайте условие

Решим эту задачу с помощью формулы пути…
Вот так у вас задача должна быть оформлена в тетради, запишите (прохожу, проверяю)

Молодцы справились, а теперь попробуйте решить следующую задачу сами. (читаем условие, разбираем что известно и что надо найти), оформите решение данной задачи как предыдущую.

Проверим, так ли у вас получилось? (вылетает решение) (проверяю)

Ребята, а в каких единицах ещё может измеряться расстояние, а скорость? Хорошо. А как изменить условие этой задачи, чтобы она решалась не сразу?
Вот один такой пример (560000м = 560 км)

Какую формулу мы использовали для решения задач? Прочитайте.

Как найти скорость, если известно расстояние и время?

Как найти время, если известно расстояние и скорость?

4.Закрепление

Чтобы отправиться в Японию, сначала из Курска мы должны попасть в Москву, потому что в Москве находятся все международные аэропорты (на карте рисую стрелку).

В Москву мы поедим на поезде. Для получения билета на поезд вы должны выполнить задание на компьютере.

Н.В. – техника безопасности (проверяем) – физкультминутка для глаз.

Все получили билеты, садитесь на свои места.

Ребята, посмотрите на карту, наша страна Россия – огромная, а Япония небольшое островное государство. И для того чтобы попасть в Токио- столицу Японии – вам надо из Москвы долететь до Владивостока, а из Владивостока долететь в Токио (показываю на карте стрелкой).

Вот такое расстояние вам надо преодолеть, но сначала его надо найти, а заодно и время, которое вы будите в полёте.

Для этого решим задачу (основная задача)

Вы можете использовать программу калькулятора для проверки правильности вычислений (проверяем, помогаем).

Кто первым вправился – поощрительная картинка.

А теперь всё внимание на доску – проверим (решение на доске).

Вы получаете билет на самолет! Давайте пристегнемся, выровняли спинку, закрыли глаза, полетели!!!

Итак, мы в Японии, нас встречает столица этой страны – город Токио. Посмотрите, какие красивые здесь места. А как вы думаете, почему мы прилетели именно в Японию? Да, правильно и у вас различные образцы техники, которую делают в Японии. А какие марки компьютеров производят в Японии?

Итог урока:

Что вам запомнилось на уроке?
Какую формулу мы использовали для решения задач? (прочитайте)
Как найти скорость, если известно расстояние и время?
Как найти время, если известно расстояние и скорость?

Посчитайте, сколько поощрительных картинок вы получили за урок.

У кого 2, вы получаете…

У кого 3…

Д/З.: Выберите страну или город, в который вы бы хотели поехать, и придумайте 3 задачи, который будут решаться с помощью формулы пути.

Урок окончен.

Презентация к уроку по алгебре (5 класс) на тему: Формулы 5 класс

Слайд 1

5 класс. Формулы

Слайд 2

Жила-была загадочная принцесса Формула. Она была непоседа и постоянно путешество- вала из государства Алгебра в государство Геометрия. Она имела множество имён и так часто менялась, что подданные не узнавали её в лицо. То она Формула Пути, то Формула для Вычисления Площади Прямоугольника. Она очень добра и всегда готова помочь тому, кто не только узнаёт её с первого взгляда, но и знает наизусть все её имена. Потому что ФОРМУЛА – это…

Слайд 3

ПРАВИЛА Как найти площадь прямоугольника, если известны его стороны? Как найти периметр прямоугольника, если известны его стороны? Что общего в записанных предложениях? ФОРМУЛЫ P = a + a + b + b или P = 2(a + b) S = a ∙ b s = v ∙ t Как найти пройденный путь, если известны время и скорость движения? a b Как записать эти правила на математическом языке? Правило, записанное на математическом языке, – это формула Площадь прямоугольника равна произведению длин его сторон Периметр прямоугольника равен сумме длин его сторон Пройденный путь – это произведение скорости на время движения

Слайд 4

ФОРМУЛЫ P = a + a + b + b или P = 2(a + b) S = a ∙ b s = v ∙ t Формула площади прямоугольника Формулы периметра прямоугольника Формула пути В дальнейшем вы узнаете еще много новых формул…

Слайд 5

s = v ∙ t t = s : v v = s : t s = v ∙ t 12 км 120 км v = s : t 15 км/ч 6 км/ч 6 м/с t = s : v 6 ч 2 ч 10 мин 90 км 2 ч 60км/ч 3600м Формула пути.

Слайд 6

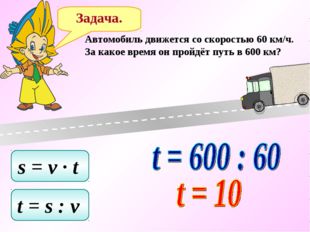
Задача. Автомобиль движется со скоростью 60 км/ч. За какое время он пройдёт путь в 600 км? s = v ∙ t t = s : v t = 600 : 60 t = 10

Слайд 7

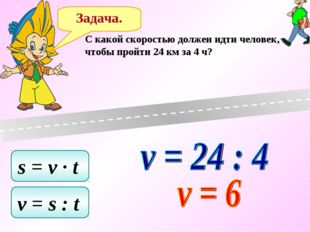
Задача. C какой скоростью должен идти человек, чтобы пройти 24 км за 4 ч? s = v ∙ t v = s : t v = 24 : 4 v = 6

Слайд 8

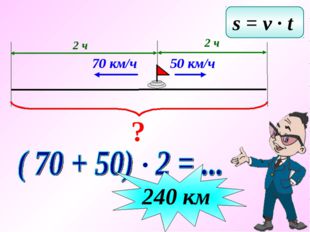
Задача. С одной станции в противоположных направлениях вышли два поезда в одно и то же время. Скорость одного поезда 50 км/ч, а другого – 70 км/ч. Какое расстояние между ними будет через 2 часа? Подсказка

Слайд 9

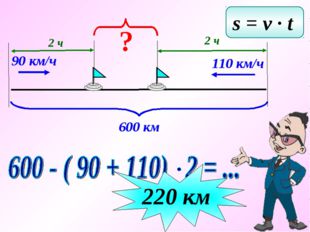
s = v ∙ t ? 2 ч 70 км/ч 50 км/ч 2 ч ( 70 + 50) 2 = … 240 км

Слайд 10

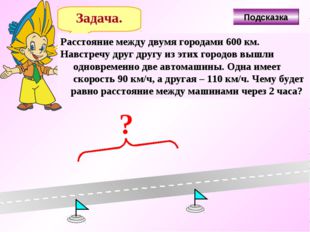
Задача. Расстояние между двумя городами 600 км. Навстречу друг другу из этих городов вышли одновременно две автомашины. Одна имеет скорость 90 км/ч, а другая – 110 км/ч. Чему будет равно расстояние между машинами через 2 часа? ? Подсказка

Слайд 11

90 км/ч 110 км/ч 600 км 2 ч 2 ч ? s = v ∙ t 600 — ( 90 + 110) 2 = … 220 км

Слайд 12

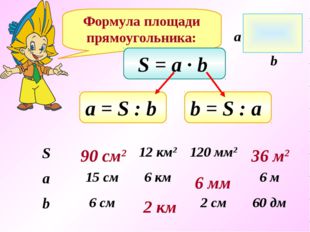
Формула площади прямоугольника. S = a ∙ b а = S : b b = S : a S 12 км 2 120 мм 2 a 15 c м 6 км 6 м b 6 см 2 см 60 дм a b 90 см 2 2 км 6 мм 36 м 2

Слайд 13

Задача. Найдите сторону прямоугольника, если его площадь 364 см 2 , а длина 26см. 364 см 2 26 см ? S = a ∙ b b = S : a b =364 : 24 b = 14

Слайд 14

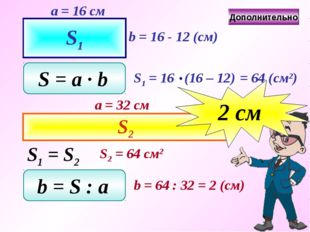
Задача. Два прямоугольника имеют равные площади. Длина первого прямоугольника 16 см, а его ширина на 12 см меньше длины. Длина второго прямоугольника 32 см. Найдите ширину второго прямоугольника. S 1 S 2 S 1 = S 2 Подсказка

Слайд 15

S 1 a = 1 6 см b = 16 — 1 2 ( см ) S = a ∙ b S 1 = 16 (16 – 1 2 ) = 64 ( см 2 ) S 2 a = 32 см S 1 = S 2 S 2 = 64 см 2 b = S : a b = 64 : 32 = 2 ( см ) 2 c м Дополнительно

Слайд 16

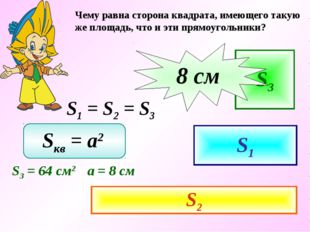
Чему равна сторона квадрата, имеющего такую же площадь, что и эти прямоугольники? S 1 S 2 S 1 = S 2 = S 3 S 3 S кв = a 2 S 3 = 64 см 2 а = 8 см а — ? 8 c м

Слайд 17

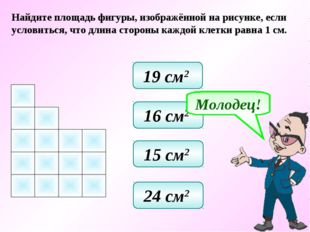
Найдите площадь фигуры, изображённой на рисунке, если условиться, что длина стороны каждой клетки равна 1 см. 19 см 2 16 см 2 15 см 2 24 см 2 Молодец!

Слайд 18

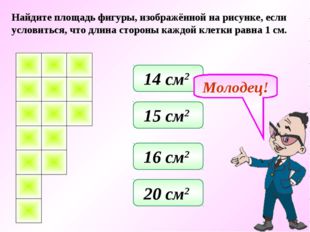
Найдите площадь фигуры, изображённой на рисунке, если условиться, что длина стороны каждой клетки равна 1 см. 20 см 2 16 см 2 15 см 2 14 см 2 Молодец!

Слайд 19

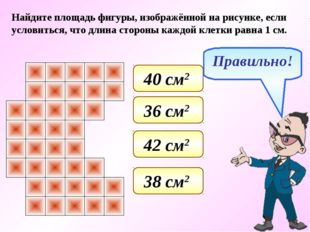
Найдите площадь фигуры, изображённой на рисунке, если условиться, что длина стороны каждой клетки равна 1 см. 42 см 2 36 см 2 38 см 2 40 см 2 Правильно!

Слайд 20

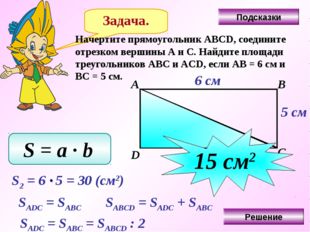
Задача. Начертите прямоугольник АВС D , соедините отрезком вершины А и С. Найдите площади треугольников АВС и АС D , если АВ = 6 см и ВС = 5 см. Подсказка (3 – 1) А В С D 6 см 5 см S = a ∙ b Решение(3 – 3) S 2 = 6 5 = 30 ( см 2 ) S ADC = S ABC S ABCD = S ADC + S ABC S ADC = S ABC = S ABCD : 2 15 см 2

Слайд 21

Формула периметра прямоугольника. P = a + a + b + b или P = 2(a + b) а 14 21 12 b 26 12 a + b 50 36 2(a + b) 72 40 8 0 2 9 100 24 72 36 24

Слайд 22

Используя формулу периметра прямоугольника, найдите: 1) Периметр Р, если а = 3м 5дм, b = 1м 2дм а = 3м 5дм = 35дм b = 1м 2дм = 12дм Р = 2(a + b) Р = 2(35 + 12) = … 94 дм

Слайд 23

Используя формулу периметра прямоугольника, найдите: 2) Сторону а, если Р = 3дм, b = 6см. Р = 3дм = 30см b = 6см Р = 2(a + b) a + b = 30 : 2 9 c м a + b = P : 2 = 15 (см) а = 15 — b а = 15 — 6

Слайд 24

Математический диктант 1 вариант 2 вариант Используя формулу s = vt , найдите неизвестную величину: 1 V ( км/ч) t ( ч) S ( км) 6 27 480 60 520 4 V ( км/ч) t ( ч) S ( км) 9 23 420 3 280 70 Используя формулу S = ab , найдите неизвестную величину : a ( м ) S ( м 2 ) 74 5 840 4 96 b ( м ) 3 a ( м ) S ( м 2 ) 94 5 92 720 4 b ( м ) 3 2

Презентация по математике на тему «Формулы»(5 класс)

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

5 класс Зайцева Нина Викторовна, МОУ Великоархангельская СОШ

2 слайд

Описание слайда:

3 слайд

Описание слайда:

Как найти площадь прямоугольника, если известны его стороны? Как найти периметр прямоугольника, если известны его стороны? Что общего в записанных предложениях? P = a + a + b + b или P = 2(a + b) S = a ∙ b s = v ∙ t Как найти пройденный путь, если известны время и скорость движения? Как записать эти правила на математическом языке? Правило, записанное на математическом языке, – это формула. Площадь прямоугольника равна произведению длин его сторон. Периметр прямоугольника равен сумме длин его сторон. Пройденный путь – это произведение скорости на время движения.

4 слайд

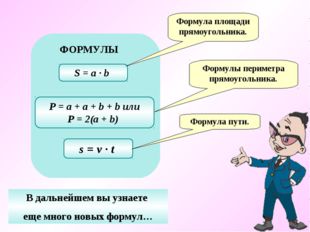
Описание слайда:

Формула площади прямоугольника. Формулы периметра прямоугольника. Формула пути. В дальнейшем вы узнаете еще много новых формул…

5 слайд

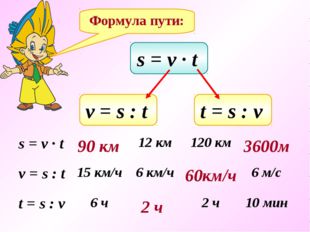
Описание слайда:

s = v ∙ t t = s : v v = s : t 90 км 2 ч 60км/ч 3600м Формула пути: s = v ∙ t 12 км 120 км v = s : t 15 км/ч 6 км/ч 6 м/с t = s : v 6 ч 2 ч 10 мин

6 слайд

Описание слайда:

Задача. Автомобиль движется со скоростью 60 км/ч. За какое время он пройдёт путь в 600 км? s = v ∙ t t = s : v

7 слайд

Описание слайда:

Задача. C какой скоростью должен идти человек, чтобы пройти 24 км за 4 ч? s = v ∙ t v = s : t

8 слайд

Описание слайда:

9 слайд

Описание слайда:

s = v ∙ t ? 2 ч 70 км/ч 50 км/ч 2 ч 240 км

10 слайд

Описание слайда:

11 слайд

Описание слайда:

90 км/ч 110 км/ч 600 км 2 ч 2 ч ? s = v ∙ t 220 км

12 слайд

Описание слайда:

Формула площади прямоугольника: S = a ∙ b а = S : b b = S : a 90 см2 2 км 6 мм 36 м2 S 12 км2 120 мм2 a 15 cм 6 км 6 м b 6 см 2 см 60 дм

13 слайд

Описание слайда:

Задача. Найдите ширину прямоугольника, если его площадь 364 см2, а длина 26см. 364 см2 26 см ? S = a ∙ b b = S : a

14 слайд

Описание слайда:

15 слайд

Описание слайда:

S1 a = 16 см b = 16 — 12 (см) S = a ∙ b = 64 (см2) S2 a = 32 см S1 = S2 S2 = 64 см2 b = S : a b = 64 : 32 = 2 (см) 2 cм Дополнительно

16 слайд

Описание слайда:

Чему равна сторона квадрата, имеющего такую же площадь, что и эти прямоугольники? S1 S2 S1 = S2 = S3 S3 Sкв = a2 S3 = 64 см2 а = 8 см а — ? 8 cм

17 слайд

Описание слайда:

18 слайд

Описание слайда:

19 слайд

Описание слайда:

20 слайд

Описание слайда:

Задача. Начертите прямоугольник АВСD, соедините отрезком вершины А и С. Найдите площади треугольников АВС и АСD, если АВ = 6 см и ВС = 5 см. Подсказки А В С D 6 см 5 см S = a ∙ b Решение = 30 (см2) SADC = SABC SABCD = SADC + SABC SADC = SABC = SABCD : 2 15 см2

21 слайд

Описание слайда:

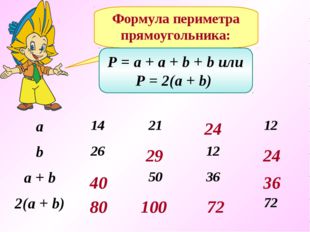
Формула периметра прямоугольника: P = a + a + b + b или P = 2(a + b) 40 80 29 100 24 72 36 24 а 14 21 12 b 26 12 a + b 50 36 2(a + b) 72

22 слайд

Описание слайда:

Используя формулу периметра прямоугольника, найдите: 1) Периметр Р, если а = 3м 5дм, b = 1м 2дм. а = 3м 5дм = 35дм b = 1м 2дм = 12дм Р = 2(a + b) Р = 2(35 + 12) = … 94 дм

23 слайд

Описание слайда:

Используя формулу периметра прямоугольника, найдите: 2) Сторону а, если Р = 3дм, b = 6см. Р = 3дм = 30см b = 6см Р = 2(a + b) a + b = 30 : 2 9 cм a + b = P : 2 = 15 (см) а = 15 — b а = 15 — 6

24 слайд

Описание слайда:

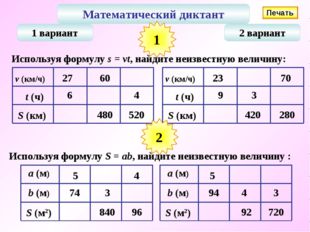
Математический диктант 1 вариант 2 вариант Используя формулу s = vt, найдите неизвестную величину: 1 Используя формулу S = ab, найдите неизвестную величину : 2 Печать

Курс профессиональной переподготовки

Учитель математики

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс:
Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник:
Все учебники

Выберите тему:
Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала:

ДВ-279566