Правила по математике 6 5 класс: Правила по математике 5-6 классы – Правила по математике 5-6 классы скачать

Правила по математике 5-6 класс

Правила по математике 5-6 класс:

1. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. ( основное свойство дроби)

2. Из двух дробей с одинаковыми знаменателями, та дробь больше, числитель которой больше.

3. Из двух дробей с одинаковыми числителями та дробь больше, знаменатель которой меньше.

4. Чтобы сравнить две дроби с разными знаменателями, их нужно привести к общему знаменателю, а затем применить правило сравнения дробей с общим знаменателем.

5. Правильная дробь меньше 1, а неправильная дробь больше или равна 1.

6. Сумма дробей с общим знаменателем есть дробь, числитель которой равен сумме числителей, а знаменатель равен знаменателю данных дробей.

7. Чтобы сложить две дроби с разными знаменателями, их надо привести к общему знаменателю, а затем применить правило сложения дробей с общим знаменателем.

8. Произведение двух дробей есть дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.

9. Чтобы умножить натуральное число на дробь, нужно числитель дроби умножить на это натуральное число, а знаменатель оставить тот же.

10. Произведение взаимно обратных чисел равно 1.

11. Чтобы разделить дробь на дробь, нужно делимое умножить на дробь, обратную делителю.

12. Чтобы разделить дробь на натуральное число, нужно её знаменатель умножить на это число.

13. Сумму натурального числа и правильной дроби называют смешанной дробью.

14. Чтобы сложить смешанные дроби, надо сложить отдельно их целые и их дробные части и полученные результаты сложить.

15. Чтобы умножить или разделить смешанные дроби, нужно записать их в виде неправильных дробей и выполнить действия с обыкновенными дробями.

16. Площадь прямоугольника равна произведению длины на ширину.

17. Периметр прямоугольника равен сумме длин сторон прямоугольника.

18. Площадь квадрата равна квадрату его стороны.

19. Периметр квадрата равен сумме сторон.

20. Объём прямоугольного параллелепипеда равен произведению трёх его измерений.

21. Чтобы сложить (вычесть) десятичные дроби, нужно:

1. уравнять в этих дробях количество знаков после запятой;

2. записать их друг под другом так, чтобы запятая была записана под запятой;

3. выполнить сложение (вычитание), не обращая внимания на запятую;

4. поставить в ответе запятую под запятой в данных дробях.

22.Чтобы умножить десятичную дробь на натуральное число, надо:

1. умножить её на это число, не обращая внимания на запятую;

2. в полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби.

22. Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.

23. Чтобы разделить десятичную дробь на натуральное число, надо:

1. разделить дробь на это число, не обращая внимания на запятую;

2. поставить в частном запятую, когда кончится деление целой части.

24. Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит в множителе после единицы.

25. Чтобы перемножить две десятичные дроби, надо:

1. выполнить умножение, не обращения внимания на запятые;

2. отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.

26. Умножить число на 0,1; 0,01; 0.001 – то же самое, что разделить его на 10, 100, 1000. Для этого надо перенести запятую влево на столько цифр, сколько нулей стоит перед единицей в множителе.

27. Чтобы разделить число на десятичную дробь, надо:

1. в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;

2. после этого выполнить деление на натуральное число.

28.Чтобы разделить десятичную дробь на 0,1; 0,01; 0,001, надо перенести в ней запятую вправо на столько цифр, сколько в делителе стоит нулей перед единицей (то есть умножить её на 10, 100, 1000).

29.Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.

30.Процентом называют одну сотую часть.

31. Средняя скорость — отношение всего пройденного пути на всё время движения.

32. Простым числом называют такое натуральное число, которое больше единицы и делится только на 1 и само на себя.

33. Если число оканчивается одной из цифр 0, 2, 4, 6, 8, то оно делится на 2.

34. Если сумма цифр числа делится на 9, то и само число делится на 9.

35. Если сумма цифр числа делится на 3, то и само число делится на 3.

36.Если две последние цифры числа нули или образуют число, делящиеся на 4, то и само число делится на 4.

37.Если число делится и на 2 и на 3, то число делится на 6.

38. Если три последние цифры числа нули или образуют число, делящееся на 8, то и само число делится на 8.

Справочные материалы по математике для 5-6 классов.

Сложение и вычитание десятичных дробей

1.Уравняйте количество цифр после запятой

2.Запишите числа столбиком так, чтобы запятая оказалась под запятой.

3.Выполните сложение или вычитание, не обращая внимания на запятые.

4.Поставьте запятую под запятыми в сумме или разности.

Пример: 2,3+13,263

13,263

2,3

Пример: 28+5,2

28,

5,2

Умножение

десятичных дробей

1. Запишите числа столбиком, не обращая внимания на запятые.

2. Выполните умножение, не обращая внимания на запятые.

3. В произведении отделить справа запятой столько цифр, сколько их в обоих множителях вместе.

Пример:

1,81

1,2

Сложение и вычитание десятичных дробей

1.Уравняйте количество цифр после запятой

2.Запишите числа столбиком так, чтобы запятая оказалась под запятой.

3.Выполните сложение или вычитание, не обращая внимания на запятые.

4.Поставьте запятую под запятыми в сумме или разности.

Пример: 2,3+13,263

13,263

2,3

Пример: 28+5,2

28,

5,2

Умножение

десятичных дробей

1. Запишите числа столбиком, не обращая внимания на запятые.

2. Выполните умножение, не обращая внимания на запятые.

3. В произведении отделить справа запятой столько цифр, сколько их в обоих множителях вместе.

Пример:

1,81

1,2

Сложение и вычитание обыкновенных дробей

1.Привести дроби к наименьшему общему знаменателю.

2.Выполнить сложение или вычитание дробей с одинаковыми знаменателями.

Пример:

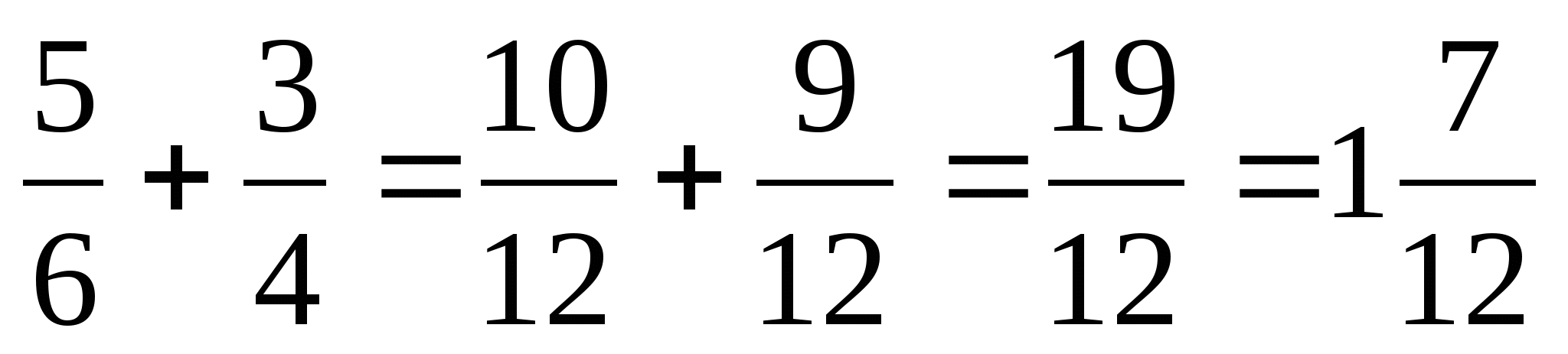
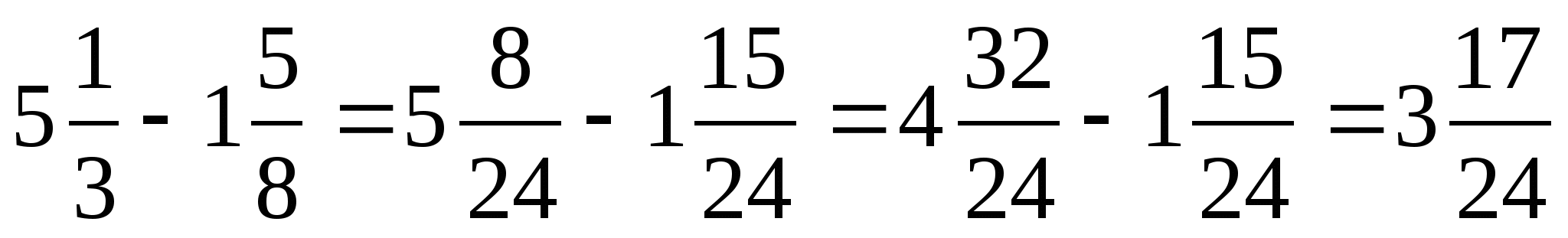
Умножение

обыкновенных дробей

1.Смешанные числа записать в виде неправильных дробей

2.Умножить числитель на числитель, знаменатель на знаменатель; если возможно выполнить сокращение дробей.

Пример:

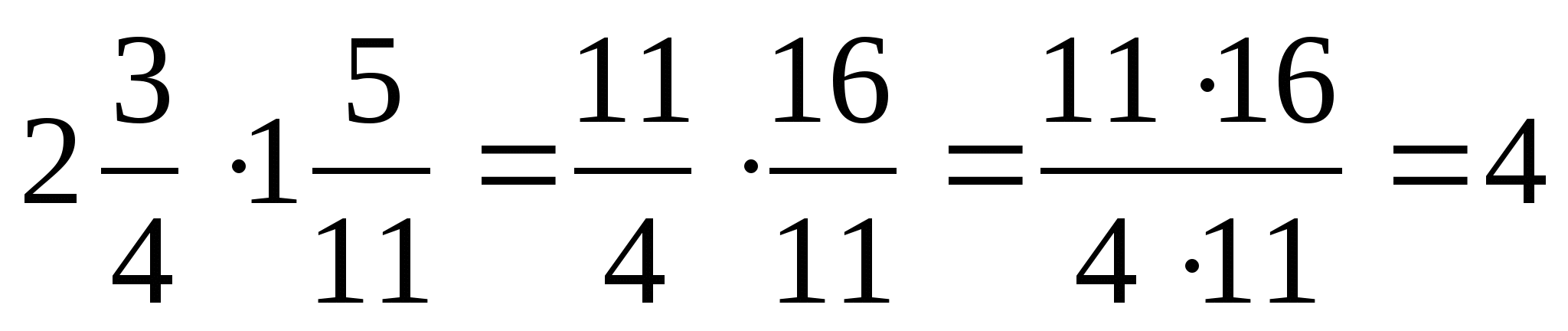
Деление

обыкновенных дробей

1.Смешанные числа записать в виде неправильных дробей

2.Первую дробь умножить на дробь, обратную второй.

Пример:

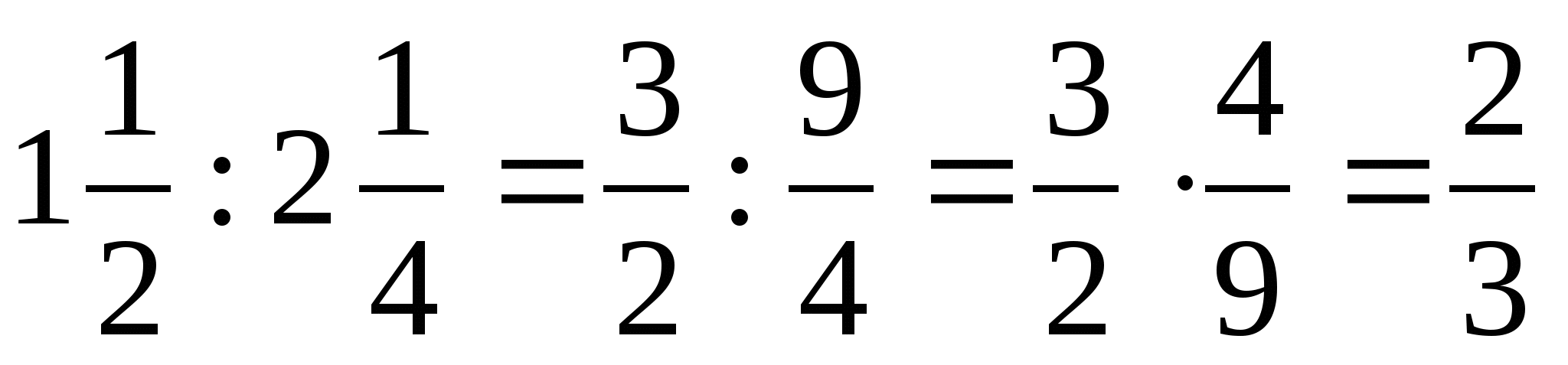
Сложение и вычитание обыкновенных дробей

1.Привести дроби к наименьшему общему знаменателю.

2.Выполнить сложение или вычитание дробей с одинаковыми знаменателями.

Пример:

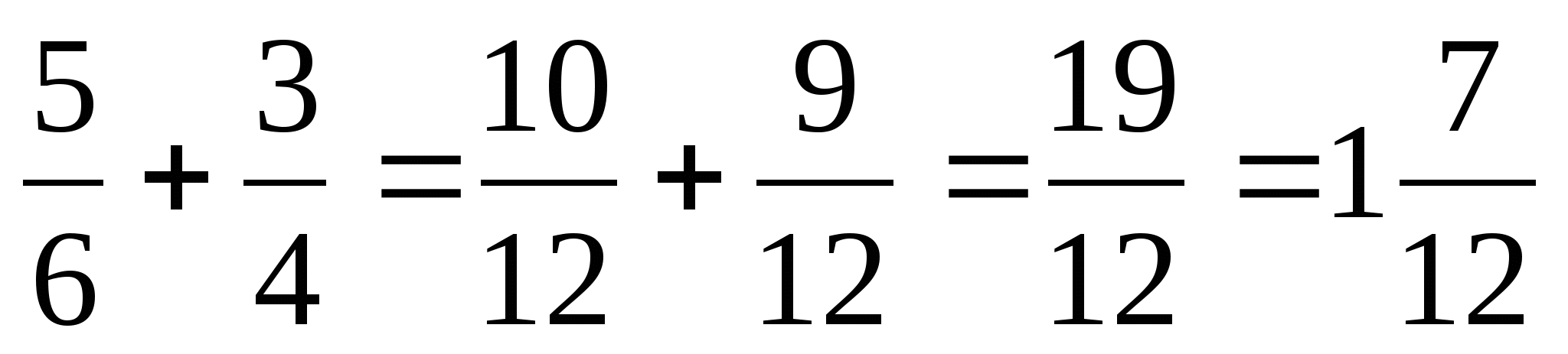
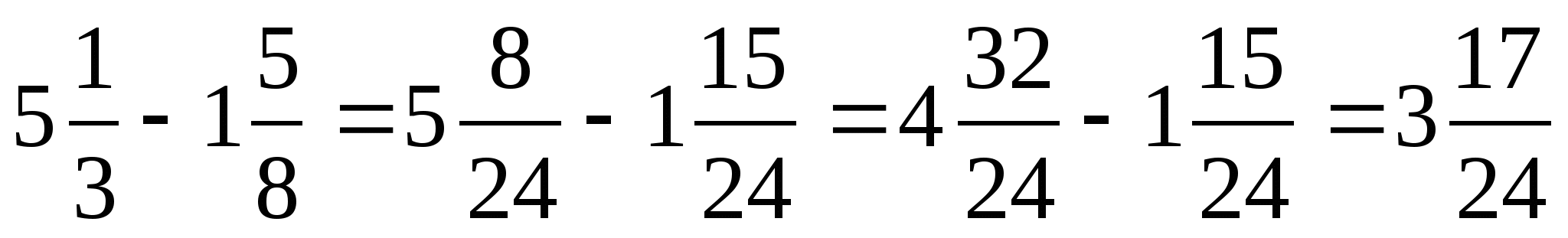
Умножение

обыкновенных дробей

1.Смешанные числа записать в виде неправильных дробей

2.Умножить числитель на числитель, знаменатель на знаменатель; если возможно выполнить сокращение дробей.

Пример:

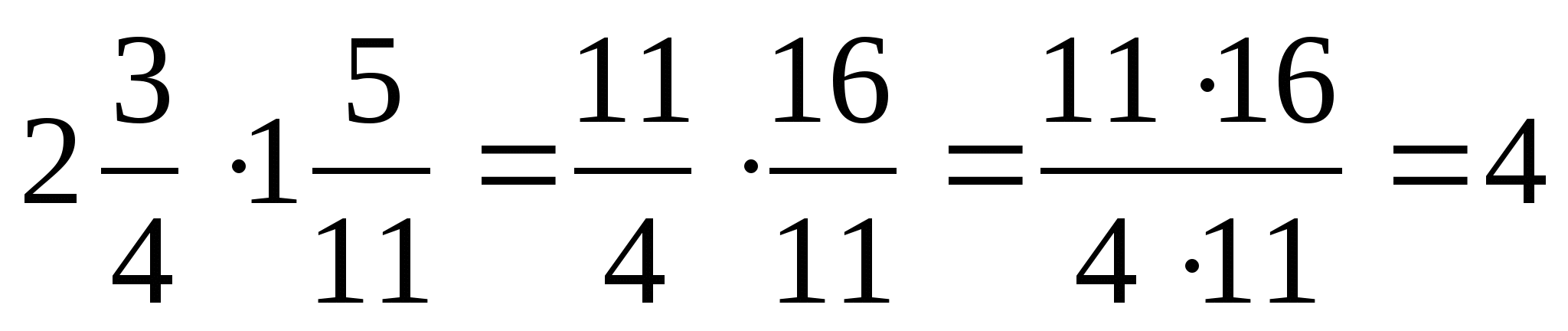
Деление

обыкновенных дробей

1.Смешанные числа записать в виде неправильных дробей

2.Первую дробь умножить на дробь, обратную второй.

Пример:

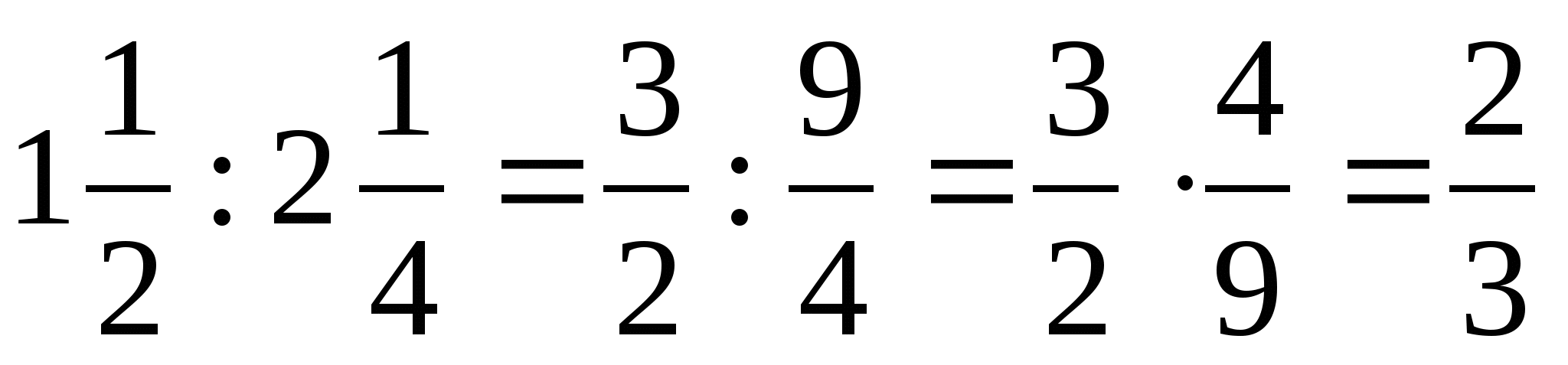
Сравнение чисел

1. Из двух отрицательных чисел меньше то, у которого модуль больше,

и больше то, у которого модуль меньше.

2. Любое отрицательное число меньше нуля.

3. Любое отрицательное число меньше любого положительного числа.

Примеры:

-3 < — 1 -2 < 0

-5 > -9 -1000 < 10

Сравнение чисел

1. Из двух отрицательных чисел меньше то, у которого модуль больше,

и больше то, у которого модуль меньше.

2. Любое отрицательное число меньше нуля.

3. Любое отрицательное число меньше любого положительного числа.

Примеры:

-3 < — 1 -2 < 0

-5 > -9 -1000 < 10

Сложение отрицательных чисел

Чтобы сложить два отрицательных числа, надо:

1) сложить их модули;

2) перед полученным числом поставить знак – .

Примеры: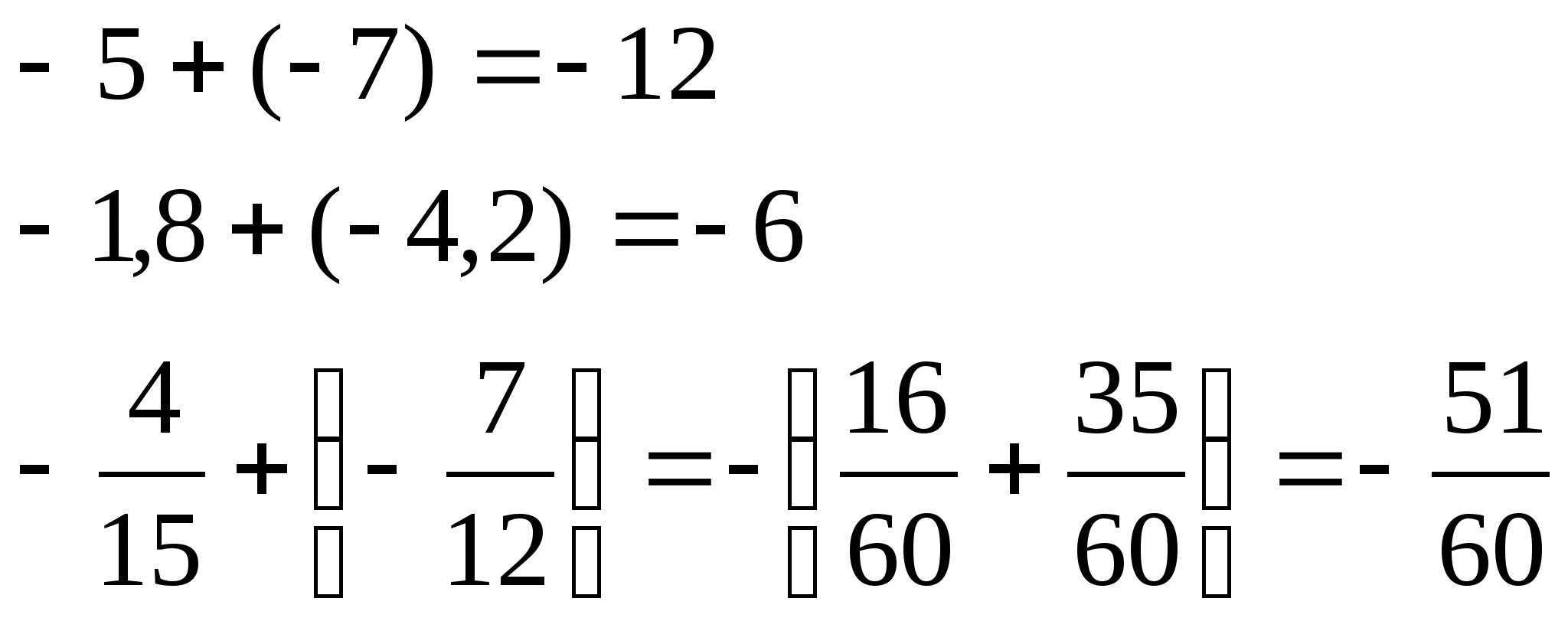

Сложение отрицательных чисел

Чтобы сложить два отрицательных числа, надо:

1) сложить их модули;

2) перед полученным числом поставить знак – .

Примеры: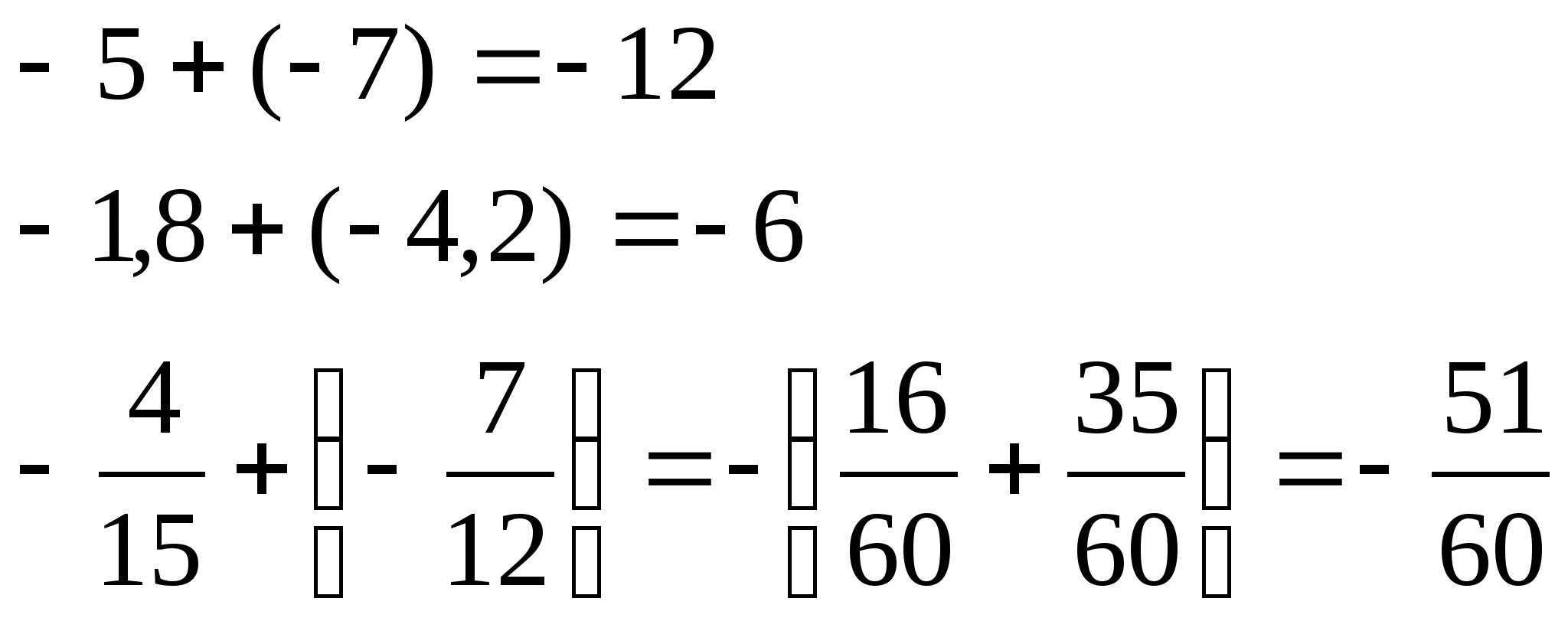

Правило округления чисел

Чтобы округлить число до нужного разряда, надо:

1)выделить разряд

2)все следующие за разрядом цифры заменить нулями, а если они стоят после запятой, то отбросить

3) — если первая после разряда цифра равна 0,1,2,3 или 4, то разрядная цифра не изменяется;

— если первая после разряда цифра равна 5,6,7,8 или 9, то разрядная цифра увеличивается на 1.

Примеры:

Округлить число 186,2753 до сотен:

1│86,2753 200

Округлить число 186,2753

до десятых:

186,2│753 186,3

Округлить число 186,2753

до тысячных:

186,275│3 186,275

Правило округления чисел

Чтобы округлить число до нужного разряда, надо:

1)выделить разряд

2)все следующие за разрядом цифры заменить нулями, а если они стоят после запятой, то отбросить

3) — если первая после разряда цифра равна 0,1,2,3 или 4, то разрядная цифра не изменяется;

— если первая после разряда цифра равна 5,6,7,8 или 9, то разрядная цифра увеличивается на 1.

Примеры:

Округлить число 186,2753 до сотен:

1│86,2753 200

Округлить число 186,2753

до десятых:

186,2│753 186,3

Округлить число 186,2753

до тысячных:

186,275│3 186,275

Правило округления чисел

Чтобы округлить число до нужного разряда, надо:

1)выделить разряд

2)все следующие за разрядом цифры заменить нулями, а если они стоят после запятой, то отбросить

3) — если первая после разряда цифра равна 0,1,2,3 или 4, то разрядная цифра не изменяется;

— если первая после разряда цифра равна 5,6,7,8 или 9, то разрядная цифра увеличивается на 1.

Примеры:

Округлить число 186,2753 до сотен:

1│86,2753 200

Округлить число 186,2753

до десятых:

186,2│753 186,3

Округлить число 186,2753

до тысячных:

186,275│3 186,275

Правило округления чисел

Чтобы округлить число до нужного разряда, надо:

1)выделить разряд

2)все следующие за разрядом цифры заменить нулями, а если они стоят после запятой, то отбросить

3) — если первая после разряда цифра равна 0,1,2,3 или 4, то разрядная цифра не изменяется;

— если первая после разряда цифра равна 5,6,7,8 или 9, то разрядная цифра увеличивается на 1.

Примеры:

Округлить число 186,2753 до сотен:

1│86,2753 200

Округлить число 186,2753

до десятых:

186,2│753 186,3

Округлить число 186,2753

до тысячных:

186,275│3 186,275

Задачи на части

Задача: Сварили джем из малины, красной и черной смородины массой 3кг. Найдите массу малины в джеме, если массовые доли ингредиентов джема относятся как 2:1:3.

Решение:   

малины красной черной

смородины смородины

2+1+3=6 – всего частей

Найдем массу одной части: 3000 г : 6 = 500г

Найдем массу малины: 2 · 500 г=1000 г=1кг

Ответ: масса малины в джеме 1кг.

Задачи на части

Задача: Сварили джем из малины, красной и черной смородины массой 3кг. Найдите массу малины в джеме, если массовые доли ингредиентов джема относятся как 2:1:3.

Решение:   

малины красной черной

смородины смородины

2+1+3=6 – всего частей

Найдем массу одной части: 3000 г : 6 = 500г

Найдем массу малины: 2 · 500 г=1000 г=1кг

Ответ: масса малины в джеме 1кг.

Задачи на части

Задача: Сварили джем из малины, красной и черной смородины массой 3кг. Найдите массу малины в джеме, если массовые доли ингредиентов джема относятся как 2:1:3.

Решение:   

малины красной черной

смородины смородины

2+1+3=6 – всего частей

Найдем массу одной части: 3000 г : 6 = 500г

Найдем массу малины: 2 · 500 г=1000 г=1кг

Ответ: масса малины в джеме 1кг.

Задачи на части

Задача: Сварили джем из малины, красной и черной смородины массой 3кг. Найдите массу малины в джеме, если массовые доли ингредиентов джема относятся как 2:1:3.

Решение:   

малины красной черной

смородины смородины

2+1+3=6 – всего частей

Найдем массу одной части: 3000 г : 6 = 500г

Найдем массу малины: 2 · 500 г=1000 г=1кг

Ответ: масса малины в джеме 1кг.

Сложение и вычитание чисел

Правило 1: Чтобы сложить два отрицательных числа,

надо:

1) сложить их модули;

2) перед полученным числом поставить знак минус.

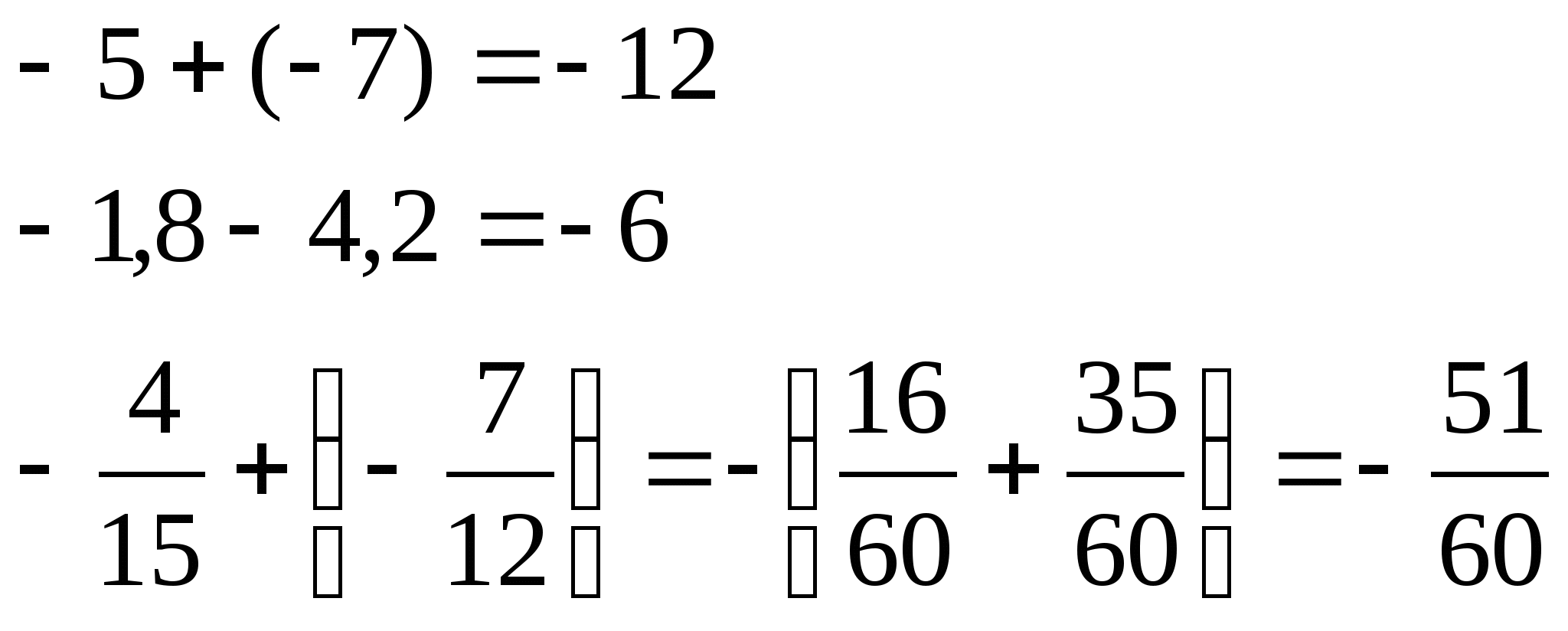
Правило 2: Чтобы сложить

отрицательное и положительное числа, надо:

1) вычесть из большего модуля меньший;

2) перед полученным числом поставить знак того числа, модуль которого больше.

Правила знаков при умножении и делении:

— · + = —

— : + = —

— · — = +

— : — = +

Как раскрыть скобки?

— ( + ) = —

+ (— ) = —

— ( —) = +

Если перед скобками стоит знак «+», то скобки можно просто опустить.

25+(4х — 1) = 25 — 4х – 1= 24 – 4х

Если перед скобками стоит знак «-», то знаки в скобках нужно изменить на противоположные и скобки опустить. 2х – (5х – 7) = 2х – 5х + 7 = — 3х + 7

Если перед скобками стоит число, то это число нужно умножить на каждое слагаемое.

5(7х-2)= 35х – 10

Решение уравнений

При переносе слагаемого из одной части уравнения в другую знак слагаемого меняется на противоположный

2х — 6= 5х-12

2х — 5х =-12+6

3.Привести подобные слагаемые

-3х=-6

4.Найти корень уравнения

х=-6:(-3)

х=2

Сложение и вычитание десятичных дробей

2.Запишите числа столбиком так, чтобы запятая оказалась под запятой.

3.Выполните сложение или вычитание

4.Поставьте запятую под запятыми

Пример: 2,3+13,263 28+5,2

13,263 28,

2,3 5,2

Умножение десятичных дробей

1. Запишите числа столбиком,

не обращая внимания на запятые.

2. Выполните умножение

3.В произведении отделить справа запятой столько цифр,

сколько их в обоих множителях вместе.

Пример: 1,81

1,2

Сложение и вычитание обыкновенных дробей

1.Привести дроби к наименьшему общему знаменателю.

Пример: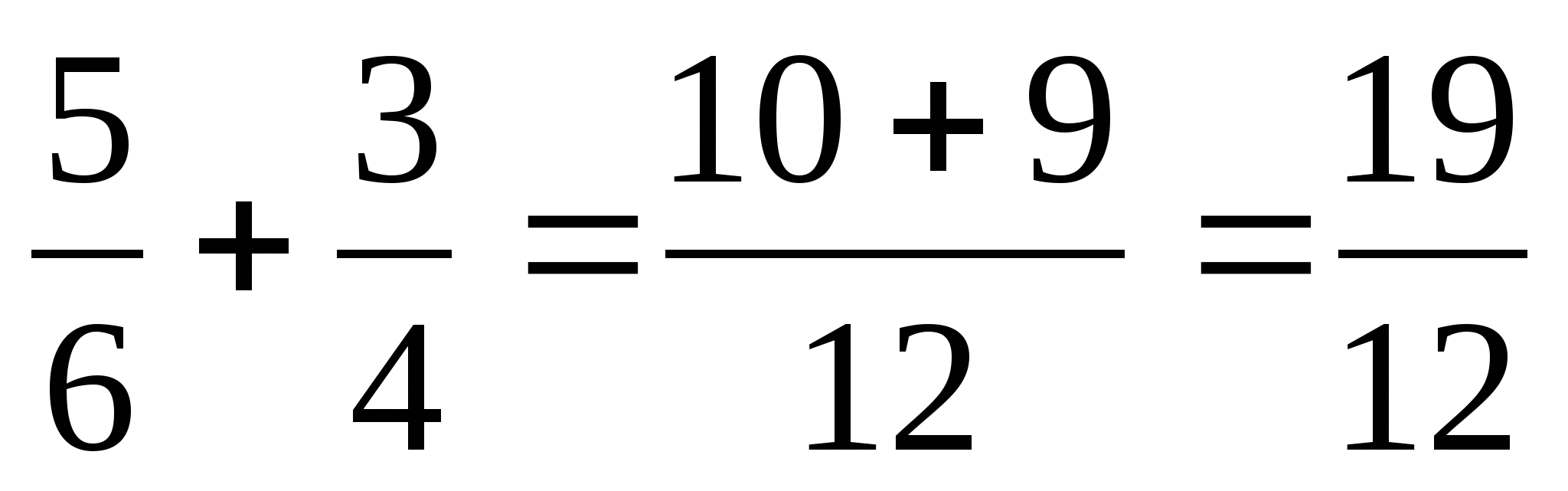

Деление обыкновенных дробей

1.Смешанные числа записать в виде неправильных дробей

2.Первую дробь умножить на дробь, обратную второй.

Пример: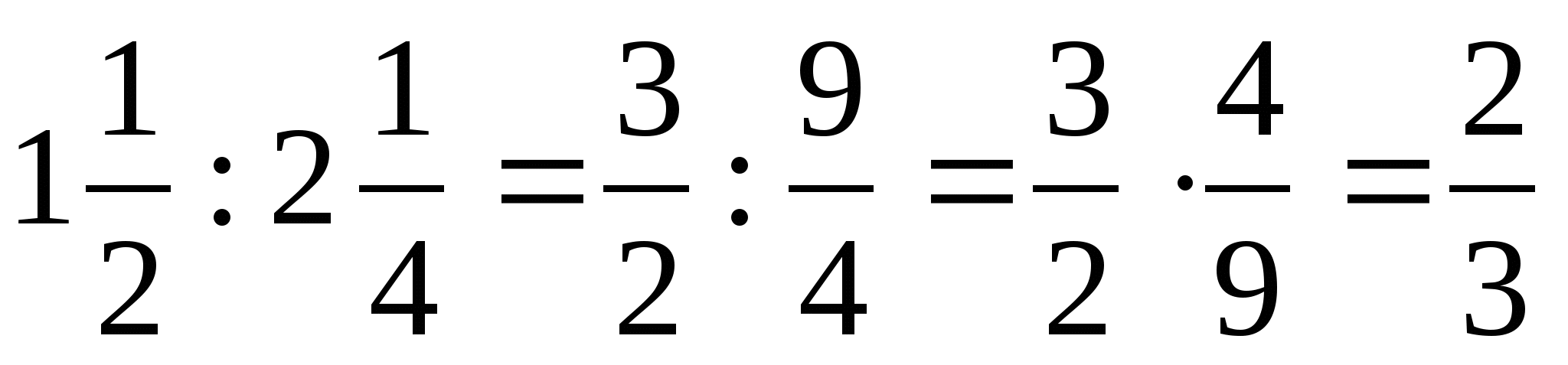

1

2

3

4

5

6

7

8

9

1

121

144

169

196

225

256

289

324

361

2

441

484

529

576

625

676

729

784

841

3

961

1024

1089

1156

1225

1296

1369

1444

1521

4

1681

1764

1849

1936

2025

2116

2209

2304

2401

5

2601

2704

2809

2916

3025

3136

3249

3364

3481

6

3721

3844

3969

4096

4225

4356

4489

4624

4761

7

5041

5184

5329

5476

5625

5776

5929

6084

6241

8

6561

6724

6889

7056

7225

7396

7569

7744

7921

9

8281

8464

8649

8836

9025

9216

9409

9604

9801

Формулы сокращенного умножения

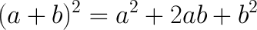
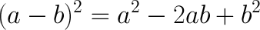
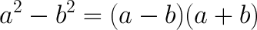
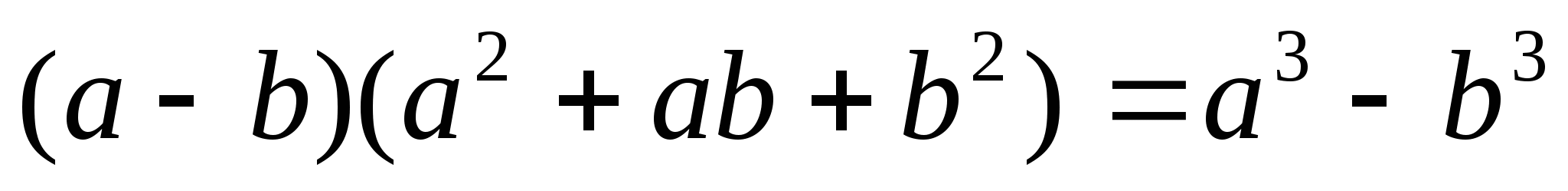
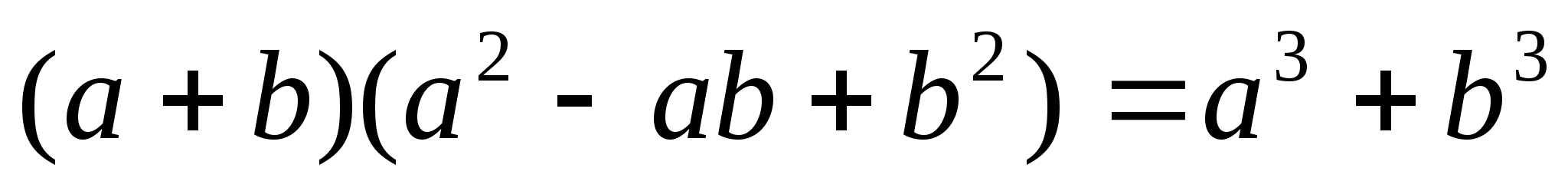
Разряды десятичных дробей

Тысячи

Сотни

Десятки

Единицы

Десятые

Сотые

Тысячные

Десятитысячные

5

6

2

7 ,

8

5

3

9

Разряды десятичных дробей

Тысячи

Сотни

Десятки

Единицы

Десятые

Сотые

Тысячные

Десятитысячные

5

6

2

7 ,

8

5

3

9

Репетитору по математике для работы в 5-6 классе — Колпаков Александр Николаевич

Предлагаю вашему вниманию страницу, на которой размещаются тематические ссылки на описания моих методик преподавания. Здесь вы найдете информацию о частных приемах, используемых репетитором математики в работе с детьми 5 — 6 классов самого разного уровня знаний и способностей: от участников математических олимпиад до сильно запущенных отстающих учеников.

Методические статьи:

Репетитор по математике о цветовой поддержке темы «вычитание».
Простой и полезный прием, помогающий удержать внимания слабого ученика на структуре алгоритма вычитания отрицательных чисел. Об использовании цвета для выделений знаков арифметических действий в длинных примерах на вычисление.

Методика повторов в условиях задач
Описание приема, которым репетитор по математике регулярно пользуется на занятиях с остающими учениками 5 — 6 классов по теме задачи на дроби. Использование одинаковых сюжетов в текстовых задачах. Один из методов улучшения концентрации внимания учащихся.

О работе репетитора по математике с признаками делимости.
Приемы, облегчающие учащимся выполнение некоторых упражнений на признаки и усвоение их доказательств (для сильных школьников). Оценка уровня сложности преподавания темы. Связь со следующим материалом. Актуальность темы. Характерные особенности заданий. Виды заданий репетитора. Математика 5 класс по Петерсону и 6 класс по Виленкину.

Рациональная дробь на уроке у репетитора по математике
Как отбиться от вопросов любознательных учеников о причинах введения того или иного определения или понятия. Мастеркласс репетитора по математике для ведения урока на тему «Рациональная дробь» (6 класс, Виленкин). Начинающему преподавателю на земетку.

Поиск наименьшего общего кратного (6 класс)
На странице рассказывается о том, почему репетитор по математике отказывается от формулировки правила находения НОКа, предложенного учебником (5 класс по Петерсону или 6 класс по Виленкину). Методы объяснений, особенности подбора слов для текстов правил. Опорные фразы репетитора, многократно повторяемые на уроках для запоминания алгоритма.

Cложение рациональных чисел с репетитором по математике О том, в каком ключе лучше провести урок на сложение отрицательных и положительных чисел со слабым учеником в 6 классе. Эффективный прием объяснения через практическую задачу о сумме денег на телефоне.

Репетитор по математике о работе с правилом вычитания отрицательных чисел. Об особенностях работы с правилом a-b=a+(-b) и приемы подачи темы отстающему ученику. Советы по оформлению решений и адаптации правила перевода вычитания в сложение. Cпособы объяснения материала и характер заданий репетитора. 6 класс.

Подготовка в Курчатовскую школу
О том, как происходит подготовка способных детей к ежегодной вступительной олимпиаде по математике (4 — 5 класс), проходящей в стенах Курчатовской школы. Особенности подготовки в соответствии с уровнем ученика. Этапы подготовки. Приемы, используемые в олимпиадной репетиторской практике.

Прием репетитора по математике в работе с задачами на движение. 5 класс.. Оформление схемок для визуального представления данных условий задач. Использование методики пропусков на уроках математики в 5 классе. Для оптимизации поиска решений задач на движение и снижения количества ошибок от невнимательности. Для работы репетитора со слабым учеником.

Как репетитор по математике оптимизирует задания на дроби
Описание особенностей изучения с репетитором одной из самых сложных тем школьного курса за 5-6 класс — текстовые задачи на части (на дроби). Методика оптимизации и сортировки информации в текстах и оформления кратких записей, важные моменты в объяснениях, обсуждение проблем преподавания. Правила, которые использует репетитор по математике в условиях занятий с учеником низких способностей.

Устный счет с репетитором по математике
Обсуждение проблем проведения устной работы с учащимися. Советы репетиторам и школьным учителям, примеры отдельных упражнений, обоснование эффективности использования устной формы работы для формирования вычислительных и мыслительных навыков. Методика организации работы на занятиях с высокой периодичностью их проведения

Репетитор по математике о задачах на дроби
Общие вопросы методики изучения текстовых задач на части и доли. Стратигия подбора подготовительных задач и приемы работы репетитора с текстами. Цветовые выделения, особенности оформление кратких записей. Спецприемы и фишечки для репетиторов. Терминология для записи правил в теоретическоую тетрадь. Типы базовых задач на дроби.

Решение уравнений в 5 — 6 классах
Методика обучения подбору действий при решении простейших типовых уравнений по программе 5 и 6 класса. Работа ученика с уменьшаемым, вычитаемым и разностью; делимым, делителем и частным; множителями и произведением, слагаемыми и суммой. Типичные проблемы слабых учеников и пути выхода репетитора из тупиковых ситуаций. Сложные случаи.

Метод умножения на 9 на пальцах

Почему я объединяю возраста? Хороший частный репетитор по математике записывает на занятия учащихся разных учебных программ. А они, как известно, отличаются порядком расположения тем. По одному пособию обыкновенные дроби умножают в 5 классе, а по другому только в 6-ом. Делить страницы по отдельным классам, во-первых технически неудобно, а во-вторых это бы сузило репетитору математики — посетителю сайта диапазон приемов для ознакомления. Почему? Большинство моих подходов имеют обобщенный и в чем то даже универсальный стержень. Некоторые заточены под скорую ликвидацию пробелов в запущенных случаях и принимаются репетитором в оборот, когда школьная программа оказывается далеко впереди от точки образования самого пробела. В каких-то материалах я привязываюсь к школьному учебнику математики, в каких-то испытываю определенную методическую свободу. Сложно и неудобно разбивать по классам. Кроме того, при разделении на страницы репетитор по математике может пропустить какой-нибудь материал. Будет искать его в 5-ом классе (в котором учится его ученик), а он окажется по другому учебнику в 6-ом.

Поэтому минимальная интеграция классов необходима. Однако, есть темы «интернациональные», которые репетиторы математики дают в одном и том же возрасте. Например, в 7 классе это формулы сокращенного умножения, в восьмом — корни. Для их методик будут сделаны узкоспециализированные страницы. Но это в перспективе. Пока ссылки классифицированы так: математика 5-6 класс, 7-8 класс, 8-9 класс, 10-11 класс, высшая математика и подготовка к ЕГЭ.

Изучайте и пользуйтесь на здоровье!
Репетитор по математике Колпаков А.Н.

Порядок выполнения действий в выражениях без скобок и со скобками

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Давайте проверим

Сравним выражения:
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Запишем.

8-3+4=5+4=9

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

8-3+4=8-7=1

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя.

Узнаем правило выполнения арифметических действий в выражениях без скобок.

Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

Потренируемся.

Рассмотрим выражение

38-10+6

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

24:3*2

В этом выражении имеются только действия умножения и деления – это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассмотрим выражение.

18:2-2*3+12:3

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

    1   4  2  5    3

18:2-2*3+12:3

Вычислим значение выражения.

    1   4  2  5    3

18:2-2*3+12:3=9-6+4=3+4=7

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.

Рассмотрим выражение.

30 + 6 * (13 — 9)

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

     3   2      1

30 + 6 * (13 — 9)

Вычислим значение выражения.

3    2   1

30+6*(13-9)=30+6*4=30+24=54

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

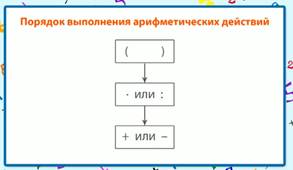
Рис. 4. Порядок действий

Потренируемся.

Рассмотрим выражения, установим порядок действий и выполним вычисления.

43 — (20 — 7) +15

32 + 9 * (19 — 16)

2 * 9 — 18:3

Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.

2*9-18:3=18-6=12

Узнаем, правильно ли определен порядок действий в следующих выражениях.

     4    3    1   2

37 + 9 — 6 : 2 * 3 =

    3       1     2

18 : (11 — 5) + 47=

   1  3       2

7 * 3 — (16 + 4)=

Рассуждаем так.

     3     4   1   2

37 + 9 — 6 : 2 * 3 =

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

     3 4  1  2

37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37

Продолжаем рассуждать.

    3    1    2

18:(11-5)+47=

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

    2    1    3

18:(11-5)+47=18:6+47=3+47=50

Рассуждаем далее.

  1  3     2

7*3-(16+4)=

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

   2  3   1

7*3-(16+4)=7*3-20=21-20=1

Выполним задание.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

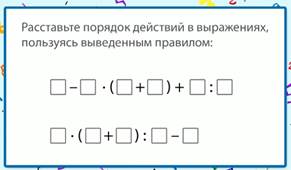
Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.

Проверим себя (рис. 6).

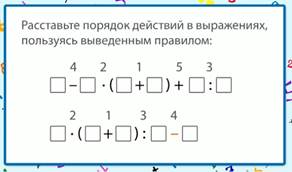
Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Festival.1september.ru (Источник).
2. Sosnovoborsk-soobchestva.ru (Источник).
3. Openclass.ru (Источник).

Домашнее задание

1. Определи порядок действий в данных выражениях. Найди значение выражений.

68+2-50+43

(36-18):(72:8)

35:5+6*2

2. Определи, в каком выражении такой порядок выполнения действий:

1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.

25+30:6-3*5+45

15+6*5-48:6-10

20+8*5-45:9+12

3. Составь три выражения, в которых такой порядок выполнения действий:

1. умножение; 2. сложение; 3. вычитание

1. сложение; 2. вычитание; 3. сложение

1. умножение; 2. деление; 3. сложение

Найди значение этих выражений.