Тренажёр по алгебре (5 класс) на тему: Отработка навыка умножения и деления. Задания для 5 класса
По теме: методические разработки, презентации и конспекты
 по математике на тему «Умножение и деление степеней», 7 класс
по математике на тему «Умножение и деление степеней», 7 класс
Материал содержит подробный конспект урока….
 Умножение и деление дробей 6 класс
Умножение и деление дробей 6 класс
Презентация, конспект урока…
 Обобщающий урок по теме «Лес». Закрепление вычислительных навыков умножения и деления трехзначных чисел на однозначное число без перехода через разряд.
Обобщающий урок по теме «Лес». Закрепление вычислительных навыков умножения и деления трехзначных чисел на однозначное число без перехода через разряд.
Пояснение к урокуВ последние годы в педагогической практике остро стал вопрос об активизации познавательной деятельности умственно отсталых школьников. Многолетняя практика педагогической работы в шко…
Урок — путешествие по теме «Умножение и деление степеней» 6 класс
Урок — путешествие по теме «Умножение и деление степеней» 6 класс…
 Конспект урока по теме «Умножение и деление степеней» 7 класс
Конспект урока по теме «Умножение и деление степеней» 7 класс
Урок в 7 классе по теме «Умножение и деление степеней»….
 Презентация к уроку «Умножение и деление степеней». 7 класс.
Презентация к уроку «Умножение и деление степеней». 7 класс.
Презентация к уроку алгебры в 7 классе по теме «Умножение и деление степеней» (урок — закрепление)….
 Тренажер для отработки навыка программирования диалога с компьютером, 9 класс
Тренажер для отработки навыка программирования диалога с компьютером, 9 класс
Любую программу составлять нужно так, чтобы ее выполнение реализовывало диалог между компьютером и пользователем в понятной для человека форме. С этой целью для учащихся 9 класса разработана Пра…
Исследовательская работа по математике для 5 класса по теме: «Необычные способы вычислений»
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 4
г.Нелидово Тверской области

Выполнила: ученица 5а класса
Евдокимова Екатерина
Руководитель работы: Орлова Ольга Геннадьевна
2014 г.
Объект исследования:
алгоритмы счета
Предмет исследования:
процесс вычислений
Гипотеза:
овладение приемами устного счета позволит повысить качество и скорость вычислений пятиклассников
Методы исследования:
— поисковый метод с использованием научной и учебной литературы, а также поиск необходимой информации в сети Интернет;
— практический метод выполнения вычислений с применением нестандартных алгоритмов счета;
— анализ полученных в ходе исследования данных.
Цель работы:
— показать различные способы вычислений.
Задачи:
— изучить литературные источники и Интернет-источники, в которых встречаются различные приемы быстрого счета;
— найти как можно больше различных необычных способов вычислений;
-научиться применять на практике самые интересные или более лёгкие способы вычислений;
— развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала;
— провести констатирующий эксперимент, т. е. пробный диктант в 5а классе;
— сделать вывод о подтверждении или опровержении выдвинутой гипотезы.
Актуальность данной темы заключается в том, что использование нестандартных приемов в формировании вычислительных навыков усиливает интерес учащихся к математике и содействует развитию математических способностей.
Содержание:
Введение.
Основная часть.
Умножение на пальцах.
Умножение удвоением.
Крестьянский способ умножения.
Умножение способом «маленький замок».
2.5. Умножение на 11.
2.6. Умножение на 9.
2.7. Квадрат двузначных чисел, начинающихся с 5-ти.
2.8. Квадрат двузначных чисел, оканчивающихся на 5.
2.9. Умножение трёхзначного числа на 101.
2.10. Умножение на 50.
2.11.Египетский способ умножения.
2.12.Умножение чисел методом «ревность».
2.13.Новый способ умножения(таблица Оконешникова).
3. Практическая часть.
4.Заключение. .
5.Литература.
1.ВВЕДЕНИЕ
Две стихии господствуют в математике – числа и фигуры с их бесконечным многообразием свойств и взаимосвязей. В нашей работе предпочтение отдано стихии чисел и действий с ними.
Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики, нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе.
.В своей работе я сочла важным показать не только то, что сам процесс выполнения действия может быть интересным, но и что, хорошо усвоив приёмы быстрого счета, можно поспорить и с ЭВМ.
Есть люди, умеющие невероятно быстро вычислять в уме. Они могут мгновенно умножить 21743 на 543, запомнить идущие подряд 1000 цифр, знают наизусть таблицу умножения чисел от 1 до 100, сразу отвечают, на какой день недели приходится 21 марта 4871 года, и вообще делают то, что обыкновенному человеку так же трудно, как поднять штангу, на которой повисли несколько человек. Но некоторыми приёмами, ускоряющими вычисления, может овладеть любой человек.
Я решила проверить на практике: действительно ли можно помочь классу считать быстро. Для начала я нашла в литературе необычные приемы быстрого счета, овладела ими сама и показала эти приемы одноклассникам. В данной работе я приведу некоторые способы вычислений, которыми можно пользоваться на уроках.
2.1.УМНОЖЕНИЕ НА ПАЛЬЦАХ
Древние египтяне были очень религиозны и считали, что душу умершего в загробном мире подвергают экзамену по счёту на пальцах. Уже это говорит о том значении, которое придавали древние этому способу выполнения умножения натуральных чисел (он получил название пальцевого счета).
Умножали на пальцах однозначные числа от 6 до 9. Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходил число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. После этого брали столько десятков, сколько вытянуто пальцев на обеих руках, и прибавляли к этому числу произведение загнутых пальцев на первой и второй руке.
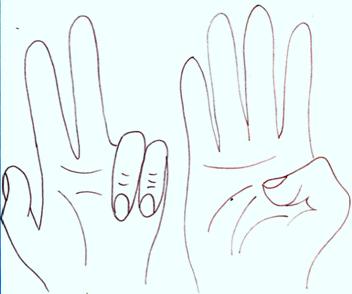
Пример: 8 ∙ 9 = 72
Позже пальцевой счёт усовершенствовали – научились показывать с помощь пальцев числа до 10000.
Умножение для числа 9 — 9·1, 9·2 … 9·10 — легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится «на пальцах». Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).
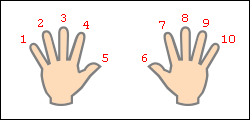
Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа — количество единиц. Слева у нас 5 пальцев не загнуто, справа — 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип «вычисления».
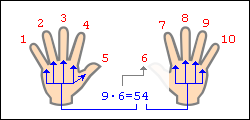
Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве «счетной машинки» не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа — 2 клеточки. Значит 9·8=72. Все очень просто.



7 клеток 2 клетки.
2.2.УМНОЖЕНИЕ УДВОЕНИЕМ
Египтяне умножение сводили к «удвоению» чисел:
37 ∙ 19
19 = 1 + 2 + 24
37 ∙ 19 = 37 ∙ (1 + 2 + 24) = 37 ∙ (1 + 2 + 2 ∙ 2 ∙ 2 ∙ 2)
37 ∙ 1 = 37
37 ∙ 2 = 74
37 ∙ 2 ∙ 2 = 148
37 ∙ 2 ∙ 2 ∙ 2 = 296
37 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 592
37 ∙ (1 + 2 + 24) = 37 + 74 + 592 = 703.
Умножение свелось к удвоениям и сложению. Это возможно всегда, так как множитель можно всегда выразить в виде суммы степеней числа 2 (и единицы, если число нечетное): для этого достаточно множитель выразить в двоичной системе.
2.3.КРЕСТЬЯНСКИЙ СПОСОБ УМНОЖЕНИЯ
Русские крестьяне применяли следующий способ умножения: Пусть надо умножить 37 на 32. Составим два столбца чисел, — один удвоением, начиная с числа 37, другой раздвоением, начиная с числа 32:
37……….32
74……….16
148……….8
296……….4
592……….2
1184……….1
Произведение всех пар соответственных чисел одинаковое, поэтому
37 ∙ 32 = 1184 ∙ 1 = 1184
В случае когда одно из чисел нечетное или оба числа нечетные, поступаем следующим образом:
24 ∙ 17
24 ∙ 16 =
= 48 ∙ 8 =
= 96 ∙ 4 =
= 192 ∙ 2 =
=384 ∙ 1 = 384
24 ∙ 17 = 24 ∙ 16 + 24 = 384 + 24 = 408
2.4.УМНОЖЕНИЕ СПОСОБОМ
«МАЛЕНЬКИЙ ЗАМОК»
Умножение чисел сейчас изучают в первом классе школы. А вот в Средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет.
За тысячелетия развития математики было придумано множество способов умножения чисел. Итальянский математик Лука Пачоли в своём трактате «Сумма знаний по арифметике, отношениям и пропорциональности»(1494 г.) приводит восемь различных методов умножения. Первый из них носит название «Маленький замок», а второй не менее романтичное название «Ревность или решетчатое умножение».
Преимущество способа умножения «Маленький замок» в том, что уже с самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину.
Цифры верхнего числа, начиная со старшего разряда, поочередно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются.

2.5.УМНОЖЕНИЕ НА 11
1 способ. Чтобы число умножить на 11, к нему приписывают 0 и прибавляют исходное число. Например:
47 * 11 = 470 + 47 = 517
243 * 11 = 2430 + 243 = 2673
2 способ. Если хочешь умножить число на 11, то поступай так: запиши число, которое нужно умножить на 11, а между цифрами исходного числа вставь сумму этих цифр. Если сумма получается двузначное число, то 1 прибавляем к первой цифре исходного числа. Например:
45 * 11 = 4(4+5)5 = 495
Такой способ подходит только для умножения двузначных чисел.
2.6.УМНОЖЕНИЕ НА 9
Чтобы умножить число на 9, к нему приписывают 0 и отнимают исходное число. Например,
241 * 9 = 2410 – 241 = 2169
847 * 9 = 8470 – 847 = 7623
2.7.КВАДРАТ ДВУЗНАЧНЫХ ЧИСЕЛ, НАЧИНАЮЩИХСЯ С 5-ТИ
Чтобы возвести в квадрат число, начинающееся на 5, надо:
К 52=25 прибавить число единиц «а».
К полученному числу приписать справа квадрат единиц.
562=(25+6)*(62)=3136
592=(25+9)*(92)=3481
2.8.КВАДРАТ ДВУЗНАЧНЫХ ЧИСЕЛ, ОКАНЧИВАЮЩИХСЯ НА 5
ПРАВИЛО: умножают число десятков на число, на единицу большее,
и к произведению приписывают 25.
752=(7*8) в конец произведения подписываем 25 = 5625
2.9.УМНОЖЕНИЕ ТРЁХЗНАЧНОГО ЧИСЛА НА 101
Например 125 * 101 = 12625
(увеличиваем первый множитель на число его сотен и приписываем к нему справа две последние цифры первого множителя)
125 + 1 = 126 12625
2.10.УМНОЖЕНИЕ НА 50
При умножении числа на 50 необходимо умножить его на100 и разделить
на 2 (т.к. 50=100:2)
352*50=352*100:2=35200:2=17600
2.11.ЕГИПЕТСКИЙ СПОСОБ УМНОЖЕНИЯ
Обозначения чисел, которые использовались в древности, были более или менее пригодны для записи результата счета. А вот выполнять арифметические действия с их помощью было очень сложно, особенно это касалось действия умножения (попробуй, перемножь: ξφß*τδ). Выход из этой ситуации нашли египтяне, поэтому способ получил название египетского. Они заменили умножение на любое число — удвоением, то есть сложением числа с самим собой.
Пример: 34 ∙ 5=34∙ (1 + 4) = 34∙ (1 + 2 ∙ 2) = 34 ∙ 1+ 34 ∙ 4.
Т. к. 5 = 4 + 1, то для получения ответа оставалось сложить числа, стоящие в правом столбике против цифр 4 и 1 , т. е. 136 + 34 = 170.

2.12.УМНОЖЕНИЕ ЧИСЕЛ МЕТОДОМ «РЕВНОСТЬ»
В торой способ носит романтическое название «ревность», или «решётчатое умножение».
торой способ носит романтическое название «ревность», или «решётчатое умножение».
Сначала рисуется прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали, и «…получается картинка, похожая на решётчатые ставни-жалюзи, — пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь».
Умножим этим способом 347 на 29. Начертим таблицу, запишем над ней число 347, а справа число 29.
В каждую строчку запишем произведение цифр, стоящих над этой клеткой и слева от нее, при этом цифру десятков произведения напишем над косой чертой, а цифру единиц – под ней. Теперь складываем числа в каждой косой полосе, выполняя эту операцию, справа налево. Если сумма окажется меньше 10, то ее пишем под нижней цифрой полосы. Если же она окажется больше, чем 10, то пишем только цифру единиц суммы, а цифру десятков прибавляем к следующей сумме. В результате получаем искомое произведение 10063.
3 4 7
2
9
10 0 6 3
2.13.НОВЫЙ СПОСОБ УМНОЖЕНИЯ
Интересен новый способ умножения, о котором недавно появились сообщения. Изобретатель новой системы устного счёта кандидат философских наук Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить.
По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе.
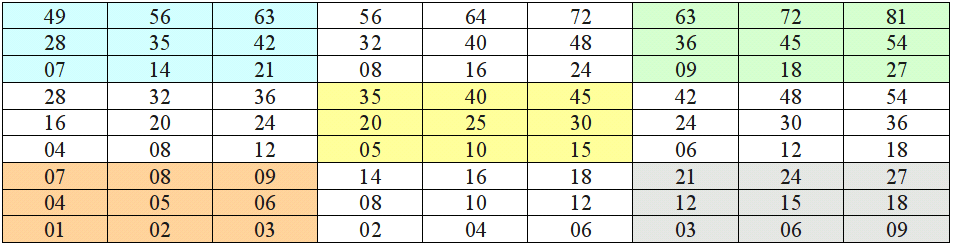
По мысли учёного, прежде чем стать вычислительным «компьютером», необходимо вызубрить созданную им таблицу. Цифры в ней распределены в девяти клетках непросто. Как утверждает Оконешников, глаз человека и его память так хитро устроены, что информация, расположенная по его методике, запоминается во-первых, быстрее, а во-вторых – намертво.
Таблица разделена на 9 частей. Расположены они по принципу мини калькулятора: слева в нижнем углу «1», справа в верхнем углу «9». Каждая часть – таблица умножения чисел от 1 до 9 (опять же в левом нижнем углу на 1, рядом правее на 2 и т.д., по той же «кнопочной» система). Как ими пользоваться?
Например, требуется умножить 9 на 842. Сразу вспоминаем большую «кнопку» 9 (она вверху справа и на ней мысленно находим маленькие кнопочки 8,4,2 (они также расположены как на калькуляторе). Им соответствуют числа 72, 36, 18. Полученные числа складываем особо: первая цифра 7 (остаётся без изменения), 2 мысленно складываем с 3, получаем 5 – это вторая цифра результата, 6 складываем с 1, получаем третью цифру -7, и остаётся последняя цифра искомого числа – 8. В результате получилось 7578.
Если при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется
на «своё» место.
С помощью матричной таблицы Оконешникова по утверждению самого автора, можно изучать и иностранные языки, и даже таблицу Менделеева.
Новая методика была опробована в нескольких российских школах и университетах. Минобразование РФ разрешило публиковать в тетрадях в клеточку вместе с привычной таблицей Пифагора новую таблицу умножения – пока просто для знакомства.
Пример: 15647 х 5
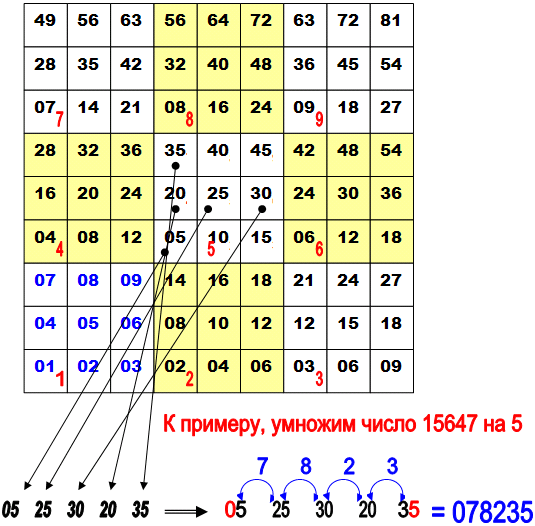
3.Практическая часть.
Изучив в литературных и Интернет источниках приёмы устного счёта, я отобрала самые распространённые и общедоступные. По согласованию с учителем математики, я составила математический диктант, опираясь на данные свойства. На уроке с разрешения учителя, я провела диктант в своём классе. В эксперименте принимали участие 6 человек. Трое выполняли вычисления обычными способами, а трое других учащихся выполняли вычисления по правилам, с которыми я их предварительно познакомила.
Образец диктанта:
1. 41*39
2. 26*34
3. 89²-11²
4. 45²
5. 28*11
6. 84*12
7. 79*11
8. 129*5
9. 64*18
10. 87*93
Проанализировав время, затраченное в среднем на выполнение задания и количество ошибок, допущенных при вычислениях, получила следующие результаты.
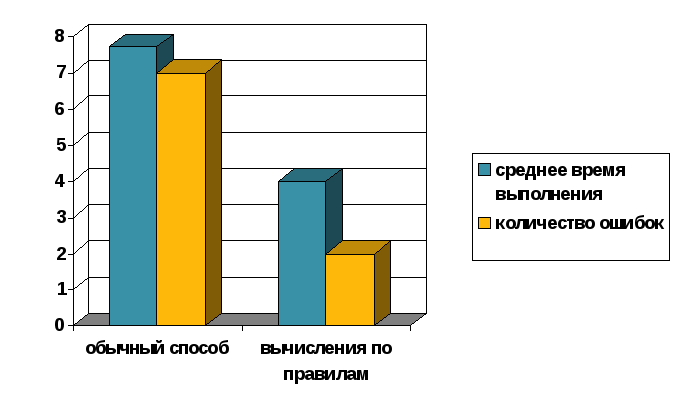
Вывод: мы видим, что наша первоначальная гипотеза о том, что знание и использование приёмов быстрого счёта позволит существенно увеличить скорость и качество счёта, подтверждается.
4.Заключение.
Работая над этой темой, я узнала, что существует много различных, забавных и интересных способов вычислений. Некоторыми в различных странах пользуются до сих пор. Но не все способы удобны в использовании, особенно при умножении многозначных чисел.
Из всех найденных мною необычных способов счета более интересными показались способы умножения на 9, 11, 101, возведение в квадрат чисел, начинающихся на 5 или заканчивающихся на 5.
Самым простым мне показался метод «удвоения и раздвоения», который использовали русские крестьяне. Я его использую при умножении не слишком больших чисел (очень удобно его использовать при умножении двузначных чисел).
Заинтересовал новый способ умножения, потому что он позволяет в уме «ворочать» огромными числами.
Вычислительная техника совершенствуется и по сей день, но любая машина делает то, что в нее закладывают люди. Работая над темой, я узнала некоторые приемы устного счета, которые помогут нам в жизни. Используя упрощенные приёмы устных вычислений, я научилась выполнять наиболее трудоёмкие арифметические действия без применения калькулятора и компьютера. Знание упрощенных приемов устных вычислений особенно важно в тех случаях, когда вычисляющий не имеет в своем распоряжении таблиц или калькулятора.
5.Литература.
1. «За страницами учебника математики» , И.Я. Депман и Н.Я. Виленкин.
М.: Просвещение,1989.
2. «Система быстрого счета по Трахтенбергу», Катлер Э. и Мак-Шейн Р.
3.«Вечера занимательной арифметики», Котов А.Я.
4. «В царстве смекалки», Игнатьев Е.И. и др.
5. Перельман Я.И. Занимательная арифметика. – М.: Транзиткнига, 2005.
6.Смирнов Ю. И. Мир чисел . Санкт-Петербург.: Мим-Экспресс 1995.
7. Энциклопедия для детей (математика) М.: Аванта .2004.
8. http://matsievsky. newmail. ru/sys-schi/file15.htm
9. http://sch69.narod. ru/mod/1/6506/hystory. html
10.Депман И. «Рассказы о математике». – Ленинград.: Просвещение, 1954. – 140 с.
11.Корнеев А.А. Феномен русского умножения. История. http://numbernautics.ru/
12.Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л., 1941.
13.http://nsportal.ru/shkola/algebra/library/priemy-bystrogo-scheta-na-urokakh-matematiki
14.http://nsportal.ru/ap/ap/drugoe/interesnye-priemy-ustnogo-scheta-0
Самостоятельная работа «Степень числа», 5 класс
Просмотр
содержимого документа
|
|
|
|
|
|
Уравнения 5 класса | Математика
Сегодня мы рассмотрим более сложные уравнения 5 класса, содержащие несколько действий. Чтобы найти неизвестную переменную, в таких уравнениях надо применить не одно, а два правила.
1) x:7+11=21
Выражение, стоящее в левой части — сумма двух слагаемых
| x:7 | + | 11 | = | 21 |
| 1сл. | 2сл. | сум. |
Таким образом, переменная x является частью первого слагаемого. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое:
x:7=21-11
x:7=10
Получили простое уравнение 5 класса, из которого надо найти неизвестное делимое. Чтобы найти неизвестное делимое, нужно частное умножить на делитель:
x=10∙7
x=70
Ответ: 70.
2) 65-5z=30
Правая часть уравнения представляет собой разность:
| 65 | — | 5z | = | 30 |
| ум. | в. | р. |
Переменная z является частью неизвестного вычитаемого. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность:
5z=65-30
5z=35
Получили простое уравнение, в котором z — неизвестный множитель. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель:
z=35:5
z=7
Ответ: 7.
3) 120:y-23=17
В правой части уравнения — разность. Переменная y является частью неизвестного уменьшаемого.
| 120:y | — | 23 | = | 17 |
| ум. | в. | р. |
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое:
120:y=17+23
120:y=40
Здесь y — неизвестный делитель. Чтобы найти неизвестный делитель, надо делимое разделить на частное:
y=120:40
y=3
Ответ: 3.
4) (48+k)∙8=400
Левая часть уравнения представляет собой произведение. Переменная k — часть первого множителя:
| (48+k) | · | 8 | = | 400 |
| 1мн | 2мн | пр |
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель:
48+k=400:8
48+k=50
В новом уравнении k — неизвестное слагаемое:
k=50-48
k=2
Ответ: 2.
Здесь мы решали уравнения 5 класса без использования свойств сложения и вычитания. В 6 классе правила раскрытия скобок упрощаются, и решать такие уравнения становится проще.
правила, свойства и примеры для 5 класса
В различных дисциплинах с физико-математическим уклоном встречается операция упрощения выражений. Иногда последние представлены в виде обыкновенных дробей. Правила деления и умножения дробных тождеств нужно знать, чтобы не совершать ошибок при вычислениях. Специалисты рекомендуют изучить теорию, а потом перейти к ее практическому применению.

Общие сведения
Многие начинающие математики путают правила работы с обыкновенными выражениями, поскольку при делении забывают «переворачивать» делитель. Некоторые не отличают обыкновенное дробное выражение от десятичного. Кроме того, следует также знать правила деления числа на определенное значение. Итак, дроби бывают только двух типов:

- Обыкновенными (правильными и неправильными).
- Десятичными (конечными и бесконечными).
Правильная — дробное выражение, у которого числитель меньше знаменателя, а у неправильного — числитель больше знаменателя (пример 2/3 и 7/3). У конечной десятичной дробной величины после запятой находится определенное количество знаков. Если же она является бесконечной, то делится на 2 типа: бесконечная периодическая (0,85 (3)) и непериодическая (1,56471238971235). Первая отличается от второй повторяющимися знаками, которые следует выделять круглыми скобками 0,(36) через определенный промежуток.
Обыкновенное дробное выражение записывается в десятичной форме. Кроме того, существует и обратное утверждение: любую десятичную дробь возможно записать в виде обыкновенной. Существует еще определенный вид дробных чисел, называющихся смешанными. Они состоят из целой части и обыкновенной дроби, т. е. 4 (½). Деление дробей в 5 классе требует некоторых подготовительных операций.
Подготовительные операции
Чтобы разделить одну дробную величину на другую, требуется произвести некоторые действия. Для этого следует руководствоваться правилом: любое смешанное число должно быть преобразовано в неправильную обыкновенную дробь. В этом случае математики рекомендуют воспользоваться следующим алгоритмом:

- Записать величину: 12 (2/5).
- Умножить знаменатель на целую часть, а затем прибавить числитель: 12*5+2=62.
- Записать результат в виде неправильной дробной величины: 62/5.
Обратную операцию по преобразованию неправильной дроби в смешанное число математики рекомендуют выполнять на завершающих этапах вычисления. Выполняется конвертация по такой методике:
- Записывается искомая величина: 62/5.
- Выделяется целая часть при делении: 12.
- От числителя искомого значения отнимается произведение знаменателя на величину, полученную во 2 пункте: 62−12*5=62−60=2.
- Записывается конечный результат: 12 (2/5).
Правило деления целого числа на дробь: произвести преобразование целого в дробь деление на 1, т. е. 4=4/1. Следует также рассмотреть признаки делимости чисел. Они помогут правильно вычислять выражения и быстро сократить полученный результат. К ним относятся:

- На 1 делится любое число без остатка.
- Если последняя цифра является четной, величину возможно разделить на 2.
- Величина делится на 3, когда сумма ее цифр делится на это значение.
- Число делится на 4, когда сумма двух крайних справа цифр можно разделить на последнее.
- Если величина заканчивается на 5 или 0, значит, 5 является ее делителем.
- Деление на 6 выполняется нацело в том случае, когда выполняются второе и третье правила.
- Чтобы разделить величину на 7, нужно от произведения всех цифр, не затрагивая последнюю, отнять двойной разряд единиц. В этом случае результат должен делиться на семерку.
- При делении на 8 нужно соблюдение второго и четвертого условий.
- Если число делится на 9, то на нее должна делиться и сумма цифр, составляющих искомую величину.
Математики рекомендуют заготовить специальные карточки на плотной бумаге или в виде презентаций на компьютере. Для этих целей может подойти программа PowerPoint, входящая в расширенный выпуск Microsoft Office.
Описанных рекомендаций будет достаточно, чтобы выполнить деление обыкновенных дробей. Правило, которое используется при этой операции, включает в себя преобразование величин, выполнение вычислений, а затем приведение к общему виду.
Деление и умножение дробей
При делении обыкновенных дробей рекомендуется на начальных этапах использовать алгоритм. Последний не понадобится, когда учащийся выполняет операцию большое количество раз. Методика имеет следующий вид:

- Записать 2 дроби: 3 (2/5) и 12 (2/5).
- Преобразовать их в неправильные дробные выражения: (5*3+2)/5=17/5 и (12*5+2)/5=62/5.
- Развернуть делитель (вторую дробь) и сменить знак деления «:» на противоположный (*), сократив на «5»: (17/5)*(5/62)=17/62.
- Упростить результат при необходимости.
Деление целого значения на дробь выполняется по такому же алгоритму. При умножении обыкновенных дробных величин нет необходимости их переворачивать. Методика является очень простой и сводится к перемножению числителей и знаменателей, а затем результат упрощается.
Таким образом, для выполнения операций деления и умножения двух обыкновенных дробей рекомендуется изучить признаки делимости, алгоритмы и определения, а затем переходить к практике.




















