Примеры для вычисления 5 класс: Материал по алгебре (5 класс) по теме: Карточки+ ответы по теме:»Арифметические примеры в несколько действий с натуральными числами» 5 класс – Примеры по математике 5 класс

Задание для 5 класса (примеры на все действия)

Задание: Расшифруй фамилию известного учёного, именем которого был назван язык программирования. Вычислите результат и расположите полученные числа в порядке убывания

С

630:9+10

Ь

(24*6+16):7

А

137-99+19

П

45+122-27

Л

15*8-9*8

К

125-72+8

А

27*5-41

Задание: Расшифруй фамилию известного учёного, именем которого был назван язык программирования. Вычислите результат и расположите полученные числа в порядке убывания

С

630:9+10

Ь

(24*6+16):7

А

137-99+19

П

45+122-27

Л

15*8-9*8

К

125-72+8

А

27*5-41

Задание: Расшифруй фамилию известного учёного, именем которого был назван язык программирования. Вычислите результат и расположите полученные числа в порядке убывания

С

630:9+10

Ь

(24*6+16):7

А

137-99+19

П

45+122-27

Л

15*8-9*8

К

125-72+8

А

27*5-41

Задание: Расшифруй фамилию известного учёного, именем которого был назван язык программирования. Вычислите результат и расположите полученные числа в порядке убывания

С

630:9+10

Ь

(24*6+16):7

А

137-99+19

П

45+122-27

Л

15*8-9*8

К

125-72+8

А

27*5-41

ОТВЕТЫ:

Задание: Расшифруй фамилию известного учёного, именем которого был назван язык программирования. Вычислите результат и расположите полученные числа в порядке убывания

С

630:9+10

80

Ь

(24*6+16):7

22,8

А

137-99+19

57

П

45+122-27

140

Л

15*8-9*8

48

К

125-72+8

61

А

27*5-41

94

С

45+122-27

140

П

Ь

27*5-41

94

А

А

630:9+10

80

С

П

125-72+8

61

К

Л

137-99+19

57

А

К

15*8-9*8

48

Л

А

(24*6+16):7

22,8

Ь

Таблицы для устного счета (5 класс)

ТАБЛИЦЫ ДЛЯ УСТНОГО СЧЁТА

МАТЕМАТИКА 5 КЛАСС

сборник

Таблицы для устного счёта, математика 5 класс, Сборник/ Сост.: В.Г. Кармазина – Макеевка : Макеевский лицей №2 «Престиж». – 20 с

Сборник предназначен для учителей математики, учащихся 5 класса.

Хорошие навыки устных вычислений –

залог успешного изучения курса школьной

математики

Одним из важных элементов урока математики является устный счёт, формирующий математическое мышление, память, вычислительные навыки и является дальнейшей опорой для усвоения математики в целом. Особенно большое внимание нужно уделять устному счёту в 5 – 6 классах школы.

Чтобы успешно формировать устные вычислительные навыки учащихся, я составила таблицы – тренажёры для устного счёта на уроках математики в 5 классе. Эти таблицы предназначены для учителей математики, работающих в 5-х классах, для тренировки учащихся в устном счёте и используются в качестве раздаточного материала на любом этапе урока на усмотрения учителя.

Таблицы имеют однотипную структуру, предусматривают задания различные по уровню сложности (с увеличением номера строки увеличивается сложность задания). Это помогает разнообразить использование таблиц, учитывать уровень подготовленности учащихся.

Каждая таблица содержит четыре варианта задания, из которых первые три предназначены для школьников со средней подготовкой устного счёта и четвёртый — для учащихся с высокими навыками.

ОГЛАВЛЕНИЕ

АННОТАЦИЯ………………………………………………………………………..6

ТАБЛИЦА 1 : СЛОЖЕНИЕ И ВЫЧИТАНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ……7

ТАБЛИЦА 2 : УМНОЖЕНИЕ И ДЕЛЕНИЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ..8

ТАБЛИЦА 3: ВСЕ ДЕЙСТВИЯ С НАТУРАЛЬНЫМИ ЧИСЛАМИ…………9

ТАБЛИЦА 4: СМЕШАННЫЕ ЧИСЛА…………………………………………10

ТАБЛИЦА 5 : СЛОЖЕНИЕ И ВЫЧИТАНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ

С ОДИНАКОВЫМ ЗНАМЕНАТЕЛЕМ…………………………11

ТАБЛИЦА 6 : СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ….12

ТАБЛИЦА 7 : УМНОЖЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ……………………13

ТАБЛИЦА 8 : ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ………………………….14

ТАБЛИЦА 9 : УМНОЖЕНИЕ И ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ

НА РОЗРЯДНУЮ ЕДИНИЦУ…………………………………..15

ТАБЛИЦА 10 : СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ…………..16

ТАБЛИЦА 11: ПРОЦЕНТЫ……………………………………………………..17

ТАБЛИЦА 12: ЕДИНИЦЫ ИЗМЕРЕНИЯ (часть1)………………………..18

ТАБЛИЦА 13: ЕДИНИЦЫ ИЗМЕРЕНИЯ (часть2)………………………..19

СЛОЖЕНИЕ И ВЫЧИТАНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ

Ф.И._______________

Ф.И.______________

Ф.И.______________

Ф.И._______________

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 3

ВАРИАНТ 4

4 + 7 =

12 – 5 =

13 – 7 =

101 – 47 =

15 – 9 =

7 + 8 =

6 + 8 =

274 + 111 =

22 – 13 =

13 + 18 =

36-19 =

304 — 217=

23 + 19 =

48 + 76 =

14 + 27 =

116 + 207 =

38 +49 =

64 – 19 =

0 + 56 =

56+67+34=

65 – 0 =

73 – 54 =

43 – 18 =

34+18+76=

43 – 28 =

56 + 78 =

54 – 0 =

132-8-42=

152 + 343 =

543 + 217 =

103 – 47 =

635+18-55=

201 – 37 =

167 – 0 =

234 + 111 =

34+77+66+33=

0 + 234 =

87 + 56 =

119 + 207 =

(68+76)+232=

23+19+7=

0 + 324 =

56+67+4=

303+(58+67)=

33+68+67=

12+75+8=

34+18+76=

178-34-28=

142-8-52=

16+ 89+11=

132-8-32=

563-(74+63)=

12+4+18+16=

675-22-75=

635+18-35=

(305+0)-45=

76+11+89+34=

23+48+2+38=

34+67+6+33=

371+(157-81)=

78-(45+18)=

32+(56+18)=

(68+76)+32=

(378+48)-68=

247-(20+47)=

(48+76)+22=

33+(58+67)=

100-67-33=

98-23-58=

326-(143+26)=

78-34-28=

1000-225-275=

(400+345)-400=

(356-0)-116=

563-(74+63)=

(45-17)-(25-17)=

(647+129)-247=

(213-40)-113=

(345+0)-45=

(34+41)+(76-41)=

(674-0)-74=

543-67-143=

381+(157-81)=

673-_____= 673

237-(37-100)=

454-(23+254)=

(378+48)-68=

203+____=9

362+(148-52)=

342+(158-42)=

245-(67+45)=

342-______+57=342

547-(110+47)=

502-(119+202)=

1000-225-275=

178-56+_______178

345+(112-____)=345

345+128-___=128

765-____+345=765

345+(342-_____)=0

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

УМНОЖЕНИЕ И ДЕЛЕНИЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ

Ф.И._____________

Ф.И.______________

Ф.И._____________

Ф.И.______________

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 3

ВАРИАНТ 4

7 · 8 =

6 · 7 =

24 : 6 =

34 · 11 =

12 · 4 =

48 : 8 =

7 · 4 =

435 : 5 =

45 : 9 =

14 · 6 =

12 : 1 =

403 · 4 =

15 · 0 =

1 · 67 =

56 · 2 =

203 · 12 =

40 · 5 =

12 : 0 =

0 · 13 =

560:14 ·7=

57 : 1 =

300 : 10 =

100 : 4 =

4 · 67· 25 =

34 · 4 =

34 : 17 =

3000 · 25 =

23 · 11· 0· 4 =

1 · 28 =

23 · 0 =

504 : 0 =

123 · 5000 =

442 : 2 =

0 : 56 =

420 : 7 =

374 : 11 =

42 : 0 =

842 : 2 =

204 · 3 =

25 · 56· 8 =

400 : 10=

2000 · 34 =

45000:100 =

4 · 76 : 4 =

1000 · 54 =

125 · 4 =

75 · 4 =

475 · 40 =

3 · 56 =

200 : 8 =

400 : 8 =

2000 : 8 =

100:4 =

403 · 8 =

23 · 11 =

17 · 17 =

400 : 8 =

45 · 11 =

12 · 12 =

225:15 · 2 =

76 · 2 · 5 =

5 · 34· 2 =

2 · 63· 5 =

231 · 11 =

24 ·3·5=

6 · 12 · 5 =

44 · 5· 0 =

20 ·507·50 =

12 · 8· 0 =

43 · 6 : 6 =

112 · 8 : 8 =

24 ·25 =

72 · 4 : 4 =

43 · 6 : 3 =

45 · 8 : 4 =

28 · 125 =

68 · 4 : 2 =

8 · 78· 25 =

307 · 12 =

18 · 0 : 18 =

8 · 37· 25 =

264 : 11 =

8 · 39· 25 =

50 · 32· 5 =

204 · 13 =

203 · 14 =

374 : 11 =

х· х = 625; х=

48 ·____ = 48

____ · 56 = 56

67 : ____ = 67

Х:6=6; х=

а· а =25; а =

а· а = 1; а =

Х · Х = 49; Х =

х· 32 =0; х=

1 · а = 1; а =

а· 6 = 0; а =

1 · Х = 1; Х =

0 · х = 0; х=

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ВСЕ ДЕЙСТВИЯ С НАТУРАЛЬНЫМИ ЧИСЛАМИ

Ф.И._____________

Ф.И.____________

Ф.И._____________

Ф.И.______________

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 3

ВАРИАНТ 4

76+19+24 =

47+18-17=

53+19+11 =

34+79+76-29=

4·23·5=

5·32·2=

2·38·5=

4·11·13·25=

34·11=

11·43=

374:11=

1212:12=

123-(51+23)=

345+(61-45)=

(123+51)-23=

179-(45+33+46)=

(347+59)-37=

167-(45+67)=

347-(59+53)=

1000-25·8=

44+53+36+47=

17·9=

403·13=

99·17=

9·12=

568:8=

9·17=

37·2+37·3-37·4=

304·7=

203·7=

1414:14=

(1212+12):12=

(44+808):4=

14·13- 14·3=

(404-88):4=

2400:(60+40)=

(505-45):5=

28·7+3·28=

(505+45):5=

202а-119а+а=

4·12+4·38=

(33+606):3=

240:(6+4)=

34х·11у=

34·12 — 34·2=

180:(6+3)=

34·12 — 34·2=

23х·4а-4х·23а=

150 : (3+2) =

234:(34-34)=

27·2+27·3+27·5=

37а·16у+16а·63у=

20х+7х=

5а+7а=

20х-7х=

79а+34в-21а=

45х+12х-х=

24а+а-19а=

45х-12х+х=

(123а-24а)·6с=

12х·5а=

14а·4х=

17х·3а=

45х-______= х

8х·34а·25=

25а·43·8с=

4х·34·25с=

24х·_____= 1000ах

123·(45- ___)=0

23а+7х =

123:(45- ___)=123

0·а=а; а=

а:123=1; а =

___:23=0

а:17=0; а =

34а:(_____- а)=1

а·а=64; а=

х·х=1; х =

а·а=0; а=

а·а=а; а=

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

СМЕШАННЫЕ ЧИСЛА

Ф.И._____________

Ф.И.____________

Ф.И.______________

Ф.И.______________

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 3

ВАРИАНТ 4

Представить в виде смешанного числа

Представить в виде смешанного числа

Представить в виде смешанного числа

Представить в виде смешанного числа

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

46 : 15 =

54 : 20 =

54 : 20 =

313 : 13 =

Представить в виде неправильной дроби

Представить в виде неправильной дроби

Представить в виде неправильной дроби

Представить в виде неправильной дроби

3 =

2 =

3 =

3 =

12 =

10 =

9 =

19 =

4 =

4 =

4 =

4 =

7 =

5 =

5 =

5 =

10 =

12 =

14 =

14 =

3 =

4 =

5 =

51 =

1 =

1 =

1 =

1 =

4 =

8 =

8 =

8 =

3

99 =

103 =

108 =

108 =

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ

С ОДИНАКОВЫМ ЗНАМЕНАТЕЛЕМ

Ф.И._____________

Ф.И._____________

Ф.И.______________

Ф.И._____________

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 3

ВАРИАНТ 4

1 —

1 +

1 —

1 +

1+

1-

1+

1-

4+

+ 5 =

12+

+ 2 =

3 —

7 —

7 —

100 —

2

7

7

4

1

9

1

3+ 4

8+ 4

13+ 4

8- 4

1

1

4

1

6 – 4=

6 – 1=

21 – 8=

6 – (1 — )=

1

1

1

(8 — 4) + 8=

4

4

7

(14 — 5)+2=

5

3

15

(5 + 4) — 2 =

– ( — ) =

– ( — ) =

+ ( — ) =

2·2 =

(1 — )+5=

(1 — )+5=

6(1 — )=

3· 3 =

(3 + 5) — 4 =

(5 + 4) — 2 =

(3 + 5) — 1 =

(3 — ) ·2=

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ

Ф.И.______________

Ф.И.______________

Ф.И.______________

Ф.И.______________

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 3

ВАРИАНТ 4

2,3 + 1,2 =

3,7 – 1,3 =

3,7 – 1,4 =

20,9+15,7 =

5,4 + 3, 7 =

0,8 – 0,4 =

2,4 + 1,2 =

12,86+1,14=

0,5 – 0,3 =

3,2 + 1, 4 =

5,6+ 1,4=

7,8-2,5=

3,8 + 1,2 =

2,7+4,3 =

1 – 0,05 =

4,1-1,6=

12 – 0,8 =

6, 7 + 2,5 =

8,23 – 4 =

12,9-7,93=

1,4 + 0,06 =

5 + 3, 9 =

2,7 + 3,5 =

13,9+16,1=

2,5 – 0,7 =

7 – 2,4 =

1,2 + 0,08 =

27,67+58,3=

7 – 3,6 =

3,2 – 1,4 =

1,2 – 0.02=

0,13-,0,013=

3,28 + 0 =

0 + 3,6 =

4,2 – 3,9 =

5-0,0003=

1,01 + 2,9 =

2,45 – 1,3 =

3,05+ 2,4 =

5,19+7,81-3,796=

4,5 – 2, 05 =

4,7-1,03 =

4,02 – 1,4 =

8,24+4,35+7,76=

1 – 0,02 =

1+0,005 =

4 – 2,03=

15,23-(4,4+5,23)=

5 – 0,013 =

1 – 0,007 =

4,7 + 2,3 =

12,12-10,1-0,02

2,14 + 4,6 =

4 – 0,023 =

7+0,7+0,007=

6,8 · 3 =

5,2–1,24 — 2,2=

4,3–1,02+1,7 =

5,4–1,8+0,6=

2,3+___=5

0,08+0,2+0,02=

2+0,04+0,4 =

8,88 – 1,8-1,08=

4 -___= 2,4

3,33-0,03-0,3

5,4+(1,6-0,04)=

3,4-2,19-0,4=

а + а= 2,4; а=

7,4 + 2,14 + 1,6 =

8,07-(1,2+0,07)=

6,7+(13,25 -6,7)=

а + а = 0,7; а=

5,2–(1,24 + 2,2)=

(4,13+1,9)-4,13=

5,4-0+0,004=

1,2а + 3,4а=

4,6 · 3 =

5,8 · 2 =

2 · 4,9 =

4,1х – 0,04х =

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

УМНОЖЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ

Ф.И.______________

Ф.И.______________

Ф.И.______________

Ф.И.______________

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 3

ВАРИАНТ 4

2 · 0,8 =

1,2 · 3 =

0,2 · 8 =

1,2 · ,5 =

1,2 · 4 =

3 · 1,4 =

1,3 · 3 =

1,12 · 4 =

0,6 · 0,3 =

0,4 · 0,3 =

0,4 · 0,3 =

0,16 · 0,3 =

2,82 · 10 =

2,2 · 0,2 =

2,02 · 0,2 =

2,82 · 0,01 =

0,15 · 0,4 =

10 · 0,34 =

0,15 · 0,4 =

0,15 · 0,04 =

0,7 · 20 =

30 · 0,2 =

0,7 · 10 =

0,07 · 200 =

100 · 1,7 =

4,08 · 2 =

20 · 1,7 =

1000 · 1,7 =

0,052 · 0,2 =

0,052 · 100 =

0,1 · 23,52 =

0,052 · 0,02 =

34,56·0,1=

34,56·0=

4 · 0,1=

34,56·0,1=

0,1 · 56=

0,1 · 15,61=

1000 · 5,6=

0 · 5,6=

0,8 · 2,5 =

4 · 2,5 =

0 · 2,5 =

0,4 · 1,2 · 2,5 =

2,08 · 1000 =

2,8 · 1000 =

0,8 · 0,25 =

2,08 · 1000 =

4,34 · 0 =

4,34 · 0 =

4,34 · 0,01 =

4,04а · 0,3 =

2,47 · 0,01 =

3,47 · 0,01 =

23,47 · 100 =

23,47с · 0,01х =

3,4 · 1,1=

1,1 · 2,6=

5,4 · 1,1=

3,7 · 1,1=

2,5 ·3 ·0,4=

2,5 ·0,3 ·8=

0,5 ·43 · 2=

3,4 · 10² =

1,2х ·5=

1,4 ·5с=

1,2х ·5=

0,4² =

2,5а ·0,2 х=

2,5а ·0,3 х=

2,5а ·0,04 х=

0,01³ =

0,5² =

0,3² =

0,4² =

0,5² · 2² =

0,2³ =

0,3³ =

0,5³ =

1 — 0,2³ =

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ

Ф.И.______________

Ф.И.______________

Ф.И.______________

Ф.И.______________

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 3

ВАРИАНТ 4

12,4 : 2 =

82,4 : 4 =

12,6 : 3 =

1,4 : 7 =

0,48 : 4 =

0,36 : 3 =

0,88 : 4 =

0,5 : 2 =

2,02 : 2 =

22,02 : 2 =

0,25 : 5 =

2,01 : 3 =

4,5 : 9 =

4,5 : 5 =

3,5 : 7 =

4,5 : 3² =

2 : 5 =

7 : 2=

4 : 8 =

1 : 25 =

4 : 100 =

4 : 10 =

24 : 100 =

4 : 100 =

0,49 : 0,7 =

0,28 : 0,7 =

0,36 : 0,6 =

0,049 : 0,7 =

1 : 0,5 =

1 : 0,2 =

1 : 0,05 =

3 : 0,05 =

3 : 0,1 =

3 : 0,01 =

23 : 0,1 =

3 : 0,01 =

2,4 : 0,001 =

12,44 : 0,01 =

23,24 : 0,001 =

2,4 : 0,1² =

0,7 : 0,35 =

0,9 : 0,45 =

0,07 : 3,5 =

0,7 : 0,35 =

2,3: 100 =

0,3 : 100 =

2: 100 =

2,3: 10³ =

0,2 : 0,4=

0,2 : 0,5=

2 : 0,5=

1 : 0,4=

0,24 : 0,6 =

0,24 : 0,4 =

0,12 : 0,6 =

0,24:0,6:0,2 =

5:0,02 =

11:0,02 =

5:0,05 =

5:(0,02:0,1) =

12,02 : 10² =

12,02 : 0,1² =

2,2 : 10² =

0,02 : 10² =

2,3 : 0,1³ =

2,3 : 10³ =

0,3 : 0,1³ =

2,3 : 0,1³ =

4:0,2² =

0,4:2² =

3:0,2² =

4:0,2² =

1:0,025 =

1:0,001 =

10:0,25 =

1:0,125 =

__·2,5 = 1

0,5 · __ = 1

__· 4 = 1

__·0,5² = 1

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

УМНОЖЕНИЕ И ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ

НА РОЗРЯДНУЮ ЕДИНИЦУ

Ф.И.______________

Ф.И.______________

Ф.И.______________

Ф.И.______________

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 3

ВАРИАНТ 4

14,16 : 10 =

35,76 · 10 =

12,13 · 10 =

10,01 : 10 =

14,16 · 0,1=

35,76 · 0,01=

12,13 :100 =

4,2·0,01 =

14,16 : 100 =

35,76 : 10 =

12,13 · 0,1 =

1000·0,2 =

14,16 : 0,1

35,76 : 0,01

12,13 : 0,1 =

0,1·45 =

0,01 · 14,16=

0,01 · 35,76=

0,001· 0,5 =

3,04 : 0 =

2,4 : 100=

1,8 · 100=

100 · 0,02 =

1000· 0,01 =

1,2 · 0,001=

1,8 : 0,001=

2,4 · 100 =

0 · 1,3 =

1,2 : 0,001=

1,8· 0,001=

2,4 : 0,001 =

0,15 : 100 =

0,5 : 100 =

5 : 100 =

2,4 : 1000 =

1: 0,001 =

0,3 · 1000=

0,3 : 0=

2,4 · 0,01=

0,009 · =

1000 · 0,4=

0,001 · 0,4=

2,4 · 0 =

0,001 : 10 =

2 : 100 =

2 : 0,01 =

1,3 · 1000=

=

2 ·0,01=

0,2 : 100=

0,005 : 10=

100·=

10 · 13,15=

1000 · 3,5=

0,012 : 0 =

0,001:2 =

4,6 : 0=

4,6 : 0,001=

2,4 : 1 =

0,5 : 0,1² =

4 : 0,01=

4 · 0,01=

4,5 · 0,001=

20 · 10^{3 =}

0 · 2,12 =

0 : 2,12 =

4,5 : 10000=

4 : =

2,5 ·0,1²=

0,5 : 0,1²=

0,2 · 10² =

· 56 =

4 : 10³=

0,4 · 10³=

0,1³· 2000 =

·=

01²·10³=

10²: 0,1³=

0,5 : 0,1² =

0,005 : ___ = 50

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ

Ф.И._____________

Ф.И.______________

Ф.И.______________

Ф.И._______________

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 3

ВАРИАНТ 4

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

= 8

= 81

= 32

=0,25

=0,36

= 1

=0

=

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ПРОЦЕНТЫ

Ф.И._____________

Ф.И._____________

Ф.И._____________

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 3

Представить в виде десятичной дроби

Представить в виде десятичной дроби

Представить в виде десятичной дроби

7% =

3% =

8% =

15% =

65% =

57% =

96% =

99% =

91% =

100%=

1%=

10%=

245%=

200%=

50%=

0,5% =

305% =

300% =

1,4% =

0,4% =

875% =

0,02% =

50% =

0,04% =

% =

% =

% =

% =

% =

% =

Представить в виде %

Представить в виде %

Представить в виде %

0,04 =

0,09 =

0,07 =

0,45 =

0,54 =

0,43 =

3,45 =

7 =

1,25 =

4,2 =

0,2 =

2 =

6 =

6,4 =

0,4 =

0,003 =

0,001 =

0,003 =

=

=

=

=

=

=

=

=

=

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ЕДИНИЦЫ ИЗМЕРЕНИЯ (часть1)

Ф.И.____________

Ф.И.____________

Ф.И.____________

Ф.И.____________

ВАРИАНТ 1

ВАРИАНТ 2

ВАРИАНТ 3

ВАРИАНТ 4

Представить в требуемых единицах

Представить в требуемых единицах

Представить в требуемых единицах

Представить в требуемых единицах

1дм = см

1м = см

1см = мм

10дм = мм

12см = мм

2дм = мм

52м = дм

82см = дм

40дм = м

80мм = см

40см = дм

450дм = м

4т = кг

17ц = кг

3 ч = мин

64т = ц

15 ц = кг

5 т = кг

200 т = ц

1,5 ц = кг

1ч = мин

1сут = ч

200 ц = т

1 мин = ч

17см = дм

85дм = м

170см = дм

107см = дм

234см = м

409см = дм

2сут = ч

2дм4см = м

349кг = ц

300см = км

78см = дм

349кг = ц

40см = мм

405г = кг

90см = мм

4м5см = км

400см= м

500см= дм

200 г= кг

2ч = сек

400см = дм

400см = км

400см = м

2400см = км

720мм= см

8000мм= дм

720 м= км

50 ч= сут

720мм = дм

72ц = кг

7,5 м = дм

720мм = дм

З0мин= ч

10мин = ч

0,5 ч= мин

10мин= ч

2,5м = дм

2,5кг = г

2,5км = м

2,5 сут = ч

4,07 м = см

4,07 км = м

4,07 дм = см

4,07 м = см

¼ ч = мин

¼ м = см

¼ т = кг

¼ м = дм

¾ м = см

¾ ч = мин

¾ сут = ч

¾ кг = г

½ т = ц

½ дм = мм

½ м = мм

½ т = ц= кг

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ЕДИНИЦЫ ИЗМЕРЕНИЯ (часть2)

Ф.И.

Ф.И.

Ф.И.

Ф.И.

ВАРИАНТ 1

Выполните действия и дайте ответ в сантиметрах если возможно

ВАРИАНТ 2

Выполните действия и дайте ответ в дециметрах

если возможно

ВАРИАНТ 3

Выполните действия и дайте ответ в метрах

если возможно

ВАРИАНТ 4

Выполните действия

5 см + 3 см=

7 дм + 5 дм=

17м – 2м =

12 дм – 8 см =

4 дм 3 см – 7 см=

2м 4 дм + 9дм=

5м 6 дм + 4дм =

5т 4ц + 4т 6ц =

3см 4мм + 5мм=

3 дм 7см – 7см=

46м 3 дм – 13дм =

2ч — 13мин =

0,5 м + 7дм=

7 2см – 12 см=

2 км 34м – 1км 4м =

3ч 48 мин + 23 мин =

2 см +0, 7 дм=

3 м + 2 м 4дм=

7 км + 4000 м =

1 км-1дм-1см=

1,5 дм – 0,4 м=

0,3м -2дм =

3 км – 1км 250 м =

0,5м +12 дм =

3м ⋅ 0,3 =

13дм ⋅ 4 =

1 км 80 + 1км20м =

0,9т – 3ц =

4 ⋅ 2 ,3 см =

12⋅5см =

0,8км – 400м =

0,5ч -24мин =

8,4 м : 3=

3 м 1 см – 14 дм 8 см=

5000м – 1,8 км =

34м8дм ⋅ 2 =

7 дм 2 см : 4=

8,5м : 5=

6м⋅ 4 =

101м :2 =

0,5м – 4дм =

0,1⋅0,6км =

100 ⋅ 0,5 м =

41м3см : 2 =

6м 18см ⋅ 0 =

1313м : 13 =

12дм ⋅ 5 =

72м ⋅ 11м =

31 м : 2м =

5,6м :7м =

150м : 3 =

0,04км ⋅ 25м =

3 дм 5 см : 0,5=

4,9м : 7 =

0,8 км : 4 =

0,5м ⋅ 3,4дм ⋅ 20см =

8⋅2 дм 5 см =

1км:2м =

54м : 0,0м =

23м 14см ⋅ 0 +0,004км =

9 см : 3 см=

2м:4 =

405 дм : 9 м =

0,5сут – 10ч – 2мин =

5 дм 6 см : 14 см=

2дм ⋅ 4дм =

12м ⋅ 4 м =

0,9м – 2см ⋅ 15 =

4см ⋅5см =

0,4м ⋅ 20см =

0,04км ⋅ 25м =

ч – 1 мин =

0,06м ⋅ 5дм =

0,9м – 2см ⋅ 15 =

56м – (12дм – 20см) =

м + 0,5м =

2 дм 4 см ⋅ 3см=

0,5м ⋅ 3,4дм ⋅ 20см =

0,025 км ⋅0,1⋅ 8 м =

12% от 1ч =

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

ОЦЕНКА:

Материал по математике (5 класс) на тему: Проверка вычислительных навыков в 5 классе.

Проверка вычислительных навыков в 5 классе 1 вариант

ФИО______________________________________________________________

Задание 1. Таблица умножения 20 примеров произвольно

1 ошибка 4, 2-5 ошибок-3

Оценка________________________

Задание 2. Вычисли устно:

Задание 3 Вычисли письменно

Проверка вычислительных навыков в 5 классе 1 вариант

ФИО______________________________________________________________

Задание 1. Таблица умножения 20 примеров произвольно

1 ошибка 4, 2-5 ошибок-3

Оценка________________________

Задание 2. Вычисли устно:

Задание 3 Вычисли письменно

Методическая разработка по алгебре (5 класс) на тему: Задание для 5 класса по математике — вычисление скорости

Задание по математике для 5 класса

  Задание на анализ условий задачи

и выделение общих существенных особенностей задачи

Тема: «Задача на определение скорости объекта по скорости второго объекта, по расстоянию и времени пути между двумя объектами»

      Условие задачи:

 В одном направлении отправились в путь пешеход и автобус. Исходное расстояние между ними — 7500 метров (пешеход на 7,5 км впереди автобуса). Скорость пешехода — 6 км/ч. Автобус догнал пешехода через 15 минут.

      Вопрос: Какова скорость автобуса?

       Решение:

 Следует наглядно показать ребёнку схему задачи — начертить пути движения автобуса и пешехода и обозначить на чертеже данные задачи. Ребёнок изначально понимает (по жизненному опыту), что автобус едет быстрее пешехода и потому быстро пешехода нагоняет.

    Далее. Мы знаем скорость пешехода и время, пройденное им — 15 минут. Что мы можем узнать? Зная время и скорость, мы узнаём расстояние, пройденное пешеходом за данное время — за 15 минут. Как? Скорость пешехода — 6 км/ч. Значит, за 1 час пешеход проходит 6 км. А за 15 минут? Какую часть от 1 часа составляют 15 минут? Одну четвёртую часть (можно нарисовать циферблат и поделить на 4 части — 15х4=60 (минут).

      Значит, первое действие: 6 (км) : 4 = 1 ½ = 1500 (м) — прошёл пешеход за 15 минут.

     Далее, мы узнаём всё  расстояние, которое проехал автобус, пока не догнал пешехода. К изначальному расстоянию между пешеходом и автобусом мы прибавляем расстояние, пройденное пешеходом до того момента, пока его не догнал автобус.

     Второе действие: 7500 + 1500 = 9000 (м) — всё расстояние, пройденное автобусом до встречи с пешеходом.

    Теперь нам известны время, пройденное автобусом (известно изначально — 15 минут), и расстояние, пройденное автобусом (9000 м). Что мы можем узнать? Конечно, скорость автобуса (ребёнок твёрдо знает, что скорость — это частное расстояния на время).

     Итак, третье действие: 9000 : 15 — 600 (м/мин) — скорость автобуса.

    Задачу мы решили, но надо бы перевести скорость из м/мин в км/ч, так как скорость пешехода изначально выражена именно в последней размерности. Как это сделать? Ребёнку надо вспомнить, сколько минут содержится в одном часе — 60 минут. А как перевести 600 м/мин в км/ч? Ведь эти 600 м/мин значит, что автобус проходит 600 метров за 1 минуту. А сколько метров он проходит за 1 час, то есть за 60 минут? Правильно — 60 раз по 600. Следовательно, надо 600 перемножить на 60. 600 х 60 = 36000 метров за 1 час. Переводим в километры: 36000 : 1000 = 36 км/ч. Следовательно, скорость автобуса — 36 км/ч. 

    Ребёнок анализирует понятие однонаправленного движения, дроби, размерность и сводимость единиц измерения. Прорабатывая и запоминая алгоритм решения задачи на вычисление скорости объекта по данной скорости другого объекта, он приобретает умение и вырабатывает навык решать задачи сходного типа.  

     Я настаиваю на том, что наглядность очень важна в данной задаче. Ребёнок должен видеть движение объектов, видеть то, что автобус нагоняет пешехода, отставая от него изначально на 7500 метров, понимать, почему автобус прошёл именно такое расстояние — расстояние от точки своего отправления до точки отправления пешехода плюс (пешеход-то уже в пути) расстояние, пройденное пешеходом.

    Эта задача диагностирует:

1) понимание ребёнком понятия дроби как части целого — 15 минут = ¼ часть целого часа; 500 метров = 2/4 = ½ часа.

2) умение и навык перевода размерности скорости из м/мин в км/ч. Очень важное умение, в котором часто путаются школьники и более старшего возраста, нежели пятиклассники. Навык этого перевода должен быть доведён до автоматизма, он должен быть тренирован несколько раз на разных примерах, можно делать и обратный перевод — из км/ч в м/мин (а потом: из км/ч в м/с и наоборот).

План-конспект урока (информатика и икт, 5 класс) по теме: Конспект урока для 5 класса по теме: «Вычисление на компьютере с помощью калькулятора. Исторические примеры различных приспособлений для выполнения арифметических операций»

5 класс

Тема урока: Вычисление на компьютере с помощью калькулятора. Исторические примеры различных приспособлений для выполнения арифметических операций.

Цели урока:

Сформировать у учащихся навыки работы с «Калькулятором»

Задачи урока:

1. познакомить учащихся с приспособлениями для вычислений древних времен;
2. познакомить учащихся с программой Калькулятор;
3. формирование умения выполнять вычисления с помощью Калькулятора

Ход урока

Мотивационный этап

Учащимся предлагается следующая ситуация. (Слайд 1)

«Вы работаете продавцом в компьютерном магазине. Покупатель — представитель крупной фирмы, приобретает:

• принтер по цене 5360 р. – 5 штук,
• сканер по цене 4600 р. – 8 штук,
• клавиатура по цене 1230 р. – 6 штук,
• колонки по цене 800 р. – 3 штуки,
• ноутбук по цене 21600 р. – 15 штук»

Вопрос к учащимся: «Сколько времени Вам понадобится, чтобы назвать покупателю итоговую сумму, при условии, что вычисления нужно производить без использования специальных устройств?»

Скорей всего понадобится достаточно много времени, так как вычисления громоздкие.

— А какими техническими средствами можно воспользоваться, чтобы ускорить процесс подсчета?

Возможные ответы: кассовый аппарат, калькулятор, телефон, компьютер.

Сегодня речь пойдет об одном из таких «помощников» — компьютерном калькуляторе.

Тема урока: «Калькулятор – помощник математиков» (Слайд 2)

Этап постановки целей урока

(Слайд 3) Сегодня на уроке мы с вами:

• узнаем, какие приспособления для вычислений использовались с древних времен;
• познакомимся с программой Калькулятор;
• выполним простые и сложные вычисления.

Этап ознакомления с новым материалом

Чтобы лучше выполнять громоздкие вычисления, люди с древних времен изобретали различные приспособления.

(Слайд 4) В Древней Греции и Древнем Риме использовали счетную доску абак.

(Слайд 5) В Древнем Китае — приспособление суан-пан,которое очень похоже на обыкновенные счеты.

(Слайд 6) До недавнего времени счетами пользовались кассиры, бухгалтеры и другие работники, чья деятельность была связана с расчетами. На протяжении столетий изобретатели совершенствовали счетные приборы.

(Слайд 7) Выдающимся изобретением французского ученого Блеза Паскаля стала механическая суммирующая машина, выполняющая сложение и вычитание.

(Слайд 8) В 1890 году начато серийное производство арифмометров Однера. К арифмометрам Однера относится знаменитый «Феликс».

(Слайд 9) В 1967 году Джек Килби вместе с двумя другими инженерами, работающими на компанию «Тексас Инструменте», создали самый первый ручной электронный калькулятор.

(Слайд 10) А теперь проверим, насколько внимательно вы слушали. Сопоставьте слова из столбцов.

На смену всем рассмотренным приспособлениям в середине XX века пришел компьютер. Одновременно был создан его «младший брат» — калькулятор.

При работе на компьютере вы можете использовать программу Калькулятор.

(Слайд 11) Посмотрите, как похожи окно этой программы и настоящий калькулятор. Если вам знаком настоящий калькулятор, то освоение виртуального не составит труда.

(Слайд 12) Запуск Калькулятора осуществляется по команде Пуск»Программы»Стандартные»Калькулятор

(Слайд 13) У Калькулятора есть два вида: обычный и инженерный. Пока что нам достаточно функций режима Обычный.

Учитель выдает каждому учащемуся вид Калькулятора, с обратной стороны – клейкая лента. Учащиеся вклеивают раздаточный материал в тетради.

(Слайд 14) Учащиеся подписывают элементы интерфейса программы

Числовые кнопки выводят в поле ввода цифры. Набирать числа можно с помощью числовой панели или дополнительного поля на клавиатуре, а также с помощью мыши в программе Калькулятор.

(Слайд 15) Обратите внимание, что некоторые знаки арифметических действий отличаются от тех, которые мы используем в математике. Попробуйте назвать их.

(Слайд 16) Проверка

(Слайд 17) Рассмотрим значения еще трех, необходимых для вычислений, кнопок.

Backspace – удаление последней введенной цифры

Пример: 467 → Backspace

результат: 46

CE – удаление последнего введенного числа

Пример: 15+2 → CE →5

результат: 20

C – полностью очищает калькулятор (кроме памяти)

Пример: 15+5 → C

результат: 0

(Слайд 18) Часто при решении сложных задач требуется запомнить промежуточный результат. Для этого в программе Калькулятор предусмотрены кнопки:

MC (Memory Clear) – очистка ячейки памяти

MR (Memory Read) – чтение из памяти

MS (Memory Set) – запись числа в память

M+ – прибавление числа из поля ввода к числу из памяти

Этап применения знаний на практике

Теперь можно приступить к практике. Начнем с простой задачи.

(Слайд 19) Крош и Ёжик решили построить башню из деталей строительного конструктора. Было использовано 154 кубика и 292 бруска. Сколько всего деталей Крош и Ёжик задействовали для строительства башни?

Задача сводится к нахождению суммы чисел 154 и 292. По предложенному алгоритму выполните вычисление

(Слайд 20) А сейчас немного магии.

Задумайте любое трехзначное число.

Запишите его в поле ввода

Умножьте задуманное число на 3

К ответу прибавьте 9

К ответу прибавьте 15

Из ответа вычтите 3

Разделите ответ на 3

Вычтите из ответа задуманное число.

У вас получилось число 7

(Слайд 21) Попробуйте самостоятельно решить предложенные задания.

• Введите число, состоящее из девяти единиц, и разделите его на 9. Каких цифр нет в получившемся числе?
• В сутках 24 часа. Сколько часов в неделе?
• 35*5+89=
• 589+235-694=
• 45*8/4=

Физкультминутка

Работа с вычислениями, выполняемыми на компьютере, требует особой внимательности и напряжения глаз. Поэтому прежде чем перейти к сложным примерам давайте проведем гимнастику для глаз (Слайд 22 — Слайд 26)

Немного отдохнули! Теперь вернемся к задаче, которую рассматривали в начале урока, но немного упростим ее. (Слайд 27). Решение задачи сводится к выражению 5360*5+4600*8=

(Слайд 28) Для начала определим порядок действий. На уроках математики вам говорили, что действия выполняются в следующем порядке: действия в скобках, умножение и деление, сложение и вычитание.

(Слайд 29) Чтобы не запутаться, будем поэтапно выполнять каждый шаг для решения этого выражения в программе.

(Слайд 30) Следующий пример также разберем вместе, чтобы запомнить алгоритм выполнения.

(122-6)*(3+5)=

(Слайд 31) Теперь попробуйте самостоятельно решить пример (124*5)+(66/2)=

Этап подведения итогов урока

(Слайд 32) Учащимся предлагается продолжить фразу:

Сегодня я узнал…

Было интересно…

Было трудно…

Я научился…

У меня получилось …

Этап постановки домашнего задания

(Слайд 33)

1.11 стр. 28

(При создании данного конспекта использовались материалы из сети Интернет)

Конспект урока «Примеры вычислений с дробями» 5 класс

План открытого урока в рамках недели молодого специалиста в МБОУ «Гимназия №3»

Учитель: Петренко Н. А.

Оборудование: учебник, карточки с индивидуальными заданиями, мультимедийный проектор.

Карточка 1.

Карточка 2.

Карточка 3.

Карточка 4.

Карточка 5.

Ход урока:

1. Организационный момент.

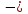Здравствуйте, ребята! На прошлом уроке мы с вами познакомились с «многоэтажными» дробными выражениями. Как мы находили значения дробных выражений (выполняли « по действиям» или «цепочкой»).

Сегодня мы продолжим работать с дробными «многоэтажными » выражениями, узнаем еще один способ вычисления таких примеров и научимся применять его в решении уравнений. Но прежде, чем приступить к изучению новой темы рассмотрим несколько примеров для разминки. А пять человек выполнят маленькую самостоятельную работу, по желанию.

2. Актуализация знаний.

Посмотрите, пожалуйста, на знаменатели дробей и на натуральное число, на которое мы умножали сумму. Что вы замечаете? Числа 3 и 2- какими эти числа являются по отношению друг к другу? (взаимно простыми). Чему равно наименьшее общее кратное взаимно простых чисел? (их произведению).

Чему равно наименьшее общее кратное чисел 3 и 2? чисел 16 и 4? чисел 3 и 4?

Вспомним, что наименьший общий знаменатель дробей, есть наименьшее общее кратное знаменателей.

3. Изучение новой темы.

– Верно ли утверждение, что значения всех данных выражений будут равны:

?

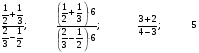– Объясните свою точку зрения.

Здесь домножили и числитель, и знаменатель дроби на 6, обратите внимание, что здесь число 6 является общим знаменателем дробей. И сразу вопрос: какое правило нам позволяет это сделать? (основное свойство дроби). Затем применили распределительный закон умножения или, говоря простым языком, раскрыли скобки, применили алгоритм умножения дроби на натуральное число, нашли значение суммы и разности в числителе и знаменателе.

Это и есть новый способ вычисления «многоэтажных» дробей. Он называется способ перехода к натуральным числам.

Алгоритм нахождения значения дробного выражения, переходя к натуральным числам.

1. Если в числителе и знаменателе сумма или разность, то домножить числитель и знаменатель на НОК всех знаменателей.

2. Применить распределительное свойство умножения.

3. Выполнить действия в числителе и знаменателе.

4. Если необходимо упростить результат.

4. Закрепление изученного.

№ 445(в, б, г)

Пример под буквой в) мы сейчас разберем вместе, и уже потом вы попробуете вычислить примеры под буквой б), и г) самостоятельно и два человека пойдут к доске.

в) = =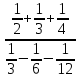

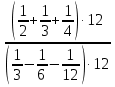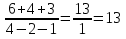
б)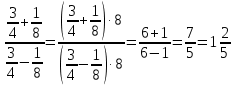

г)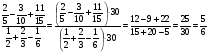

5. Физкультминутка.

Если “Да”, вы делаете наклоны вперед, руки на поясе. Если “Нет”, делаете повороты туловищем, руки за голову.

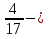правильная дробь; (да)

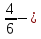несократимая дробь; (нет)

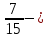несократимая дробь; (да)

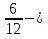правильная дробь; (да)

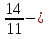правильная дробь; (нет)

Молодцы, отдохнули, теперь работаем дальше.

4. Закрепление изученного (продолжение).

Решим уравнения. Здесь мы будем пользоваться тем, что при умножении обеих частей уравнения, равенство не меняется. И так же, как и в предыдущем случае, нужно найти общий знаменатель дробей.

№ 447(1,3)

1)

;

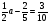Решение.

;

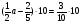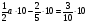
5a – 4 = 3;

5a = 3 + 4;

5a = 7;

a = 7: 5;

a = ;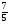

a = 1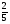

Ответ: a = 1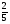

3)

;

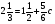Решение.

6  ;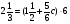

14 = 9 + 5с;

5с = 14 – 9;

5с = 5;

с = 1

Ответ: с = 1 .

5. Повторение.

Решим задачу.(если времени не останется, то устно)

Велосипедист проехал в первый час 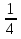пути, во второй 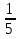пути, а в третий час 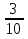пути. Какую часть пути он проехал за 3 часа? Какую часть ему еще осталось проехать?

Решение.

1) 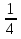+ + 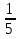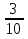= = 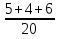= 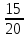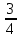(часть пути велосипедист проехал за 3 часа)

2) 1- 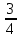= 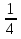(часть велосипедисту еще осталось проехать)

6. Итоги урока.

7. Домашнее задание.

№ 473(б), 475(3).

урок математики в 5 классе сложение и вычитание натуральных чисел

Тема урока: Сложение и вычитание натуральных чисел.

     Тип урока:  Обобщающий.

Оборудование: компьютер, проектор, интерактивная доска workspace.

Цели урока:

• Обобщить и систематизировать знания учащихся по теме «Сложение и вычитание натуральных чисел».
• Развитие вычислительных навыков, культуры речи;
• Воспитывать интерес к предмету, самостоятельность.

План урока

• Разминка
• Решаем примеры
• Решаем уравнения
• Решаем задачу

Ход урока.

1. Организационный момент (сообщить тему урока,  план урока, настроить на работу).

2. Разминка

Вычислите:

3. Повторение свойств сложения и вычитания натуральных чисел на интерактивной доске учащиеся соединяют ПРИМЕР-СВОЙСТВО

Свойства сложения

Свойства вычитания

1. Переместительное:   a + b = b + a

1. Вычитание суммы из числа:

a – (b + c) = a – b – c

a – (b + c) = (a – b) – c

a – (b + c) = (a – c) – b         

2. Сочетательное:    a + (b + c) = (a + b) + c

2. Вычитание числа из суммы:

(a + b) – c = (a – c) + b,  

(a + b) – c = a + (b – c)  

3. Свойство нуля:   a + 0 = a

3. Свойство нуля:  a – 0 = a     a – a = 0

4. Решаем примеры

265 + 41 + 35

937 — (137 + 793)

361 – (82 + 61)

(654 + 289) – 254

(227 + 358) – 258

— Какие выражения называются числовыми? Буквенными выражениями?- на доске учащиеся указывают числовые, буквенные выражения

5.Упростите выражение, найдите его  значение .

28 + m + 72,  при m = 87

a – 28 – 37,  при a = 265

Двое учащихся решают самостоятельно у доски, остальные в тетрадях, затем проверка решений.

6. На доске уравнения 45 +х=50                 х-40=20      

назовите уменьшаемое, вычитаемое, слагаемое в выражениях

(Как найти неизвестное уменьшаемое? слагаемое?)

7. Составьте по условию задачи уравнение:

На интерактивной доске написана задача и дан рисунок.

1. В одной корзине было несколько яиц, а в другой на 5 штук больше. Всего в двух корзинах было 37 штук яиц.

8. Тест на индивидуальных планшетах «сложение и вычитание чисел»

9. Оценки за работу на уроке:

10 Домашнее задание

Словарь

1. Сложение
2. Слагаемое
3. Сумма
4. Вычитание
5. Уменьшаемое
6. Вычитаемое
7. Разность
8. Чтобы найти….надо
9. Сочетательное свойство
10. Переместительное свойство
11. Свойство нуля
12. Решить уравнение
13. Упростить выражение
14. Решить задачу
15. Я решил
16. Я выполнил