Таблицы по математике 5 класс: Таблицы по математике 5 класс – 5-6 – 19 photos | VK

Таблицы по математике 5-6 класс

Переносите слагаемые с противоположным знаком

Задача 2 Найди число, 31% которого равен 62.

Задача 3 Сколько процентов от 75 м составляют 54 м?

10 см 1 см = 10 мм 1 дм = 10 см

1 дм 1м = 10 дм 1 км = 1 000м

ЗАДАЧИ НА ДРОБИ

Задача 1 Найти пути, длина которого равна 180 км.

Задача 2 Найти весь путь, если его равны 18 км.

Задача 3 Какую часть от пути в 7 км составляют 3 км?

пути – это 180:9=20(км)

пути – это (180:9)·4=80(км)

пути – это 18:3=6(км)

Весь путь равен (18:3)·5=30(км)

1 км– это пути

3 км – это пути

Действия с десятичными дробями

1

+

3

8,

5

0

2

2

9,

6

0

0,

7

4

0,

8

5

3

9,

2

4

3

9,

2

4

3

˟

1

8,

4

1 знак

4

5

9,

2

8

1

6

0,

1

5

2 знака

4

8

3,

7

0

5

+

9

2

0

1

1

2

1

8

4

1

1

2

2,

7

6

0

(1+2) знака

8

0

8

0

8

0

0

5

8,75· 10=8,7,5

8,75·1000=8,750,

63,4: 10=6,3,4

63,4:1000=0,063,4

6

5,92: 1,6=5,9,2:1,6,=59,2:16=3,7

59,2: 0,16=59,20,:0,16,=5920:16=370

Признаки делимости

делимость

на 2, на 5, на 10

проверяйте по последней цифре

делимость

на 3, на 9

проверяйте по сумме цифр

на 2

на 5

на 10

на 3

на 9

делится

делится

70

72

74

76

78

72310

385

13890

714

7+1+

+4=12

657

6+5+

+7=18

не делится

не делится

221

23

35

47

69

556

16054

46177

811

8+1+

+1=10

236

2+3+

+6=11

72310 делится на 5, так как 0 делится на 5

236 не делится на 9,

так как 2+3+6=11 не делится на 9

ДРОБЬ

Доля — это одна из равных частей целого

СЛОЖЕНИЕ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ

УМНОЖЕНИЕ ДРОБЕЙ

*

=

ТАБЛИЦА ДЕЛЕНИЯ

:

1

2

3

4

5

6

7

8

9

10

1

1

2

1

3

1

4

1

5

1

6

1

7

1

8

1

9

1

10

1

ЕСЛИ ДЕЛИМОЕ БОЛЬШЕ ДЕЛИТЕЛЯ – РЕЗУЛЬТАТ БОЛЬШЕ ЕДИНИЦЫ

ЕСЛИ ДЕЛИМОЕ МЕНЬШЕ ДЕЛИТЕЛЯ – РЕЗУЛЬТАТ МЕНЬШЕ ЕДИНИЦЫ

ДЕЛИМОЕ : ДЕЛИТЕЛЬ = ЧАСТНОЕ

6 : 3 = 2

Умножение и деление положительных и отрицательных чисел

Опорная таблица по курсу математики 5 класса.

Опорная таблица по курсу математики 5 класса.

Числовое выражение

980 + (980 + m)

Буквенное выражение

a + b = b + a

a + (b + c) = (a + b) +c = a + b + c

a + 0 = 0 + a = a

a – (b + c) = a – b – c

(a + b) – c = a + (b – c), если c < b или c = b

(a + b) – c = (a – c) + b, если c < a или c = a

a – 0 = a; a – a = 0

Переместительное свойство сложения

Сочетательное свойство сложения

Свойство нуля при сложении

Свойство вычитания суммы из числа

Свойство вычитания числа из суммы

Свойство нуля при вычитании

a · b = b · a

a · (b · c) = (a · b) · c

(a + b) · c = a · c + b· c

(a – b) · c = a · c – a · b

1 · n = n

0 · n = 0

Переместительное свойство умножения

Сочетательное свойство умножения

Распределительное свойство умножения относительно сложения

Распределительное свойство умножения относительно вычитания

Свойство нуля при умножении

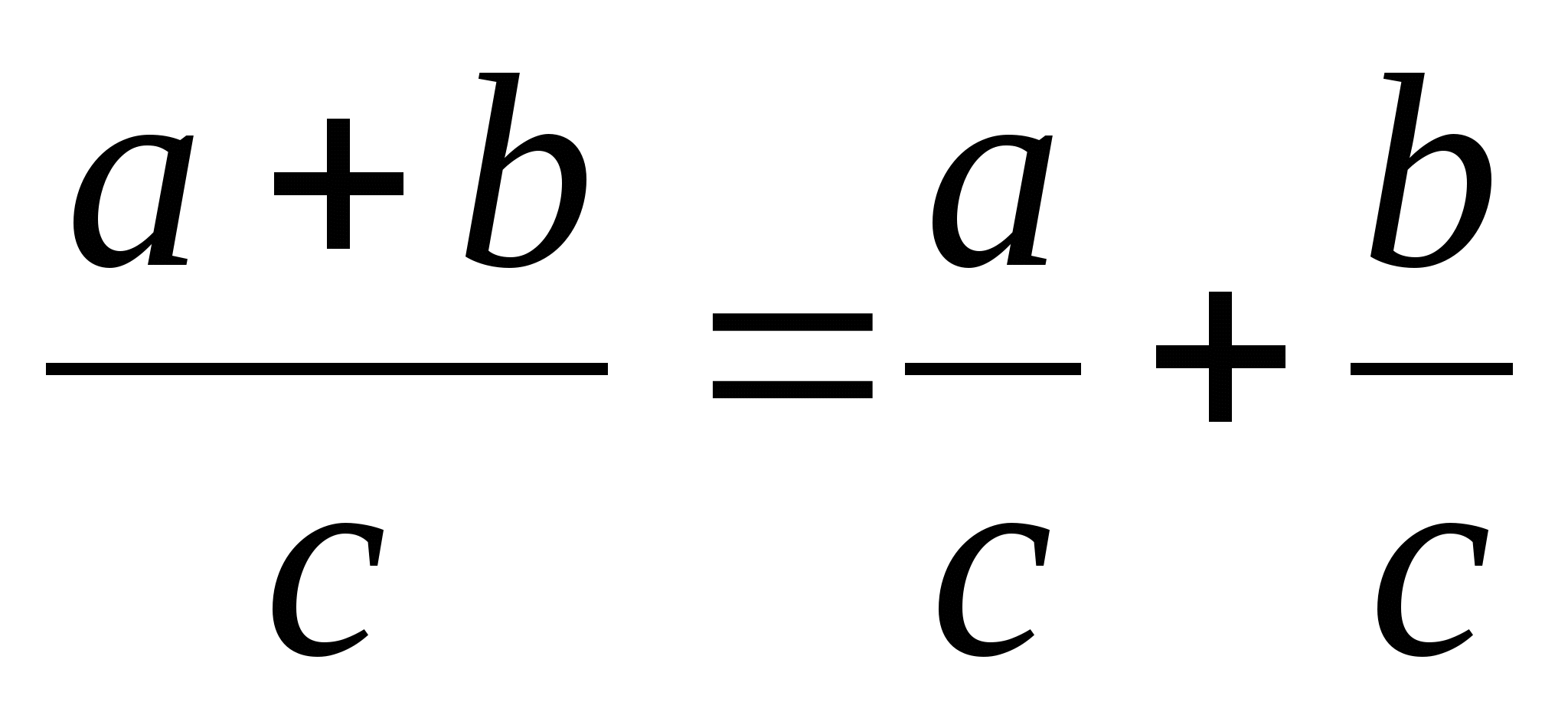
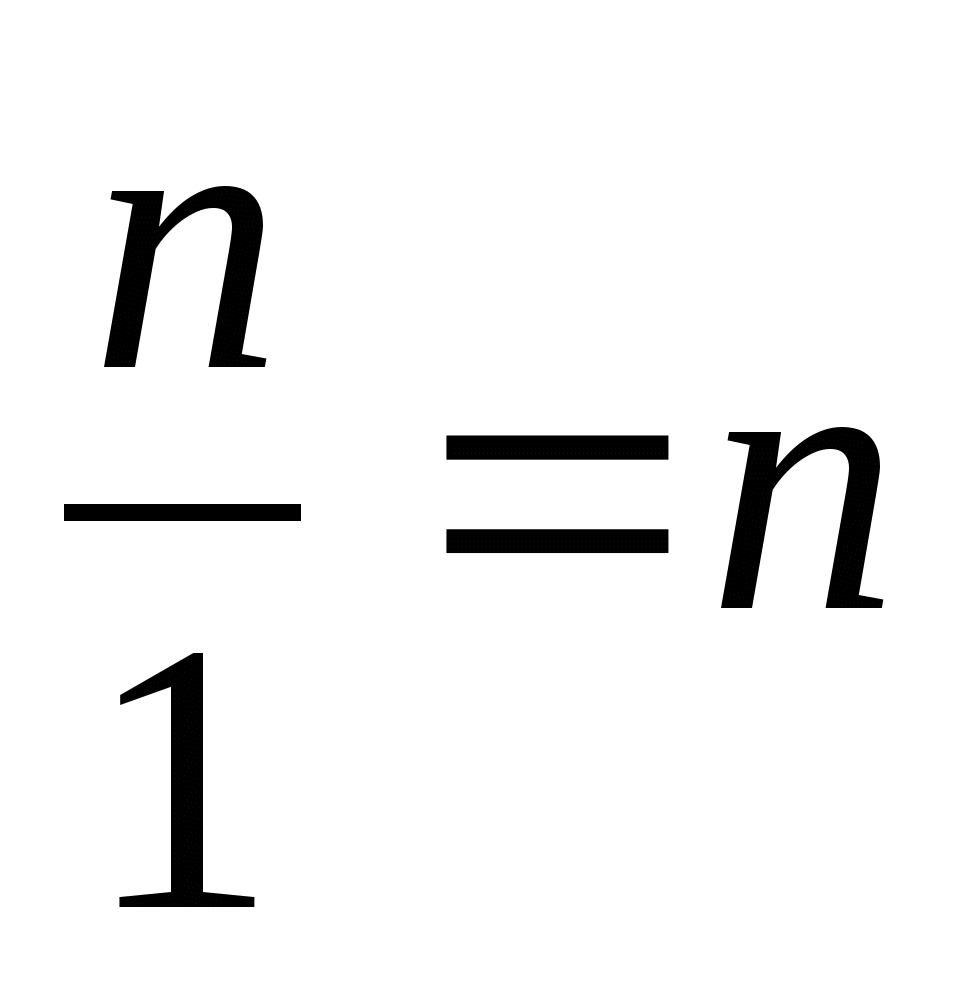
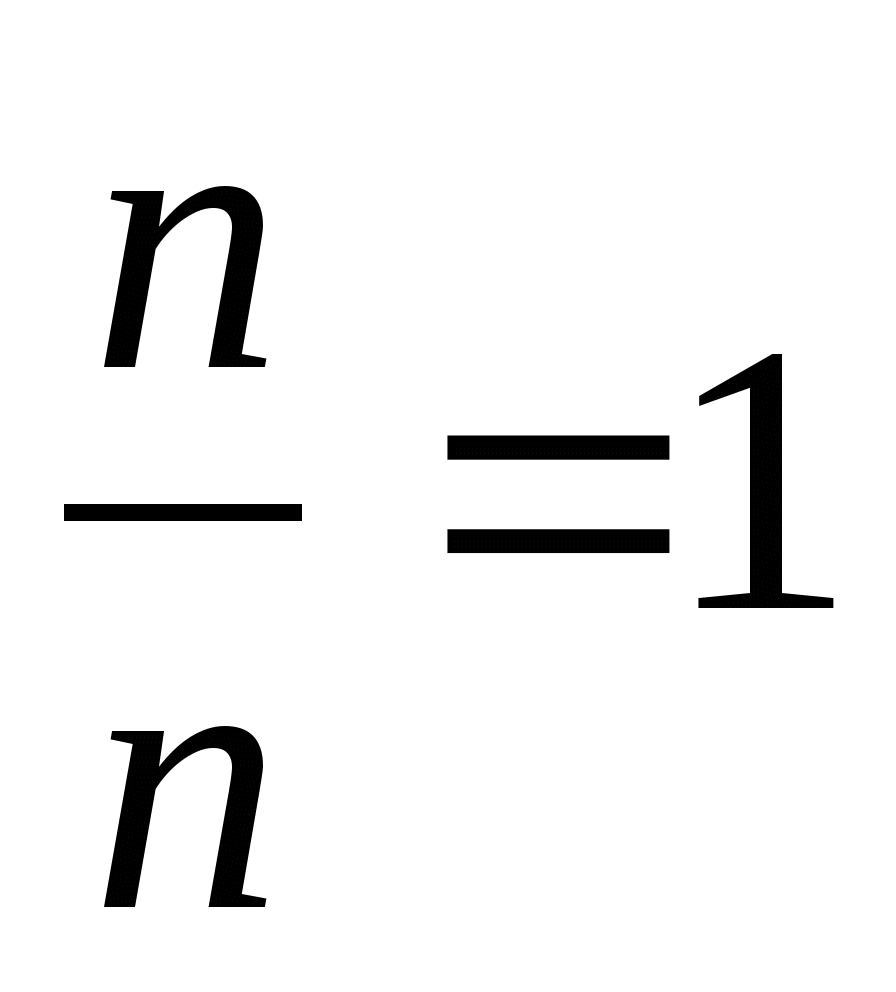
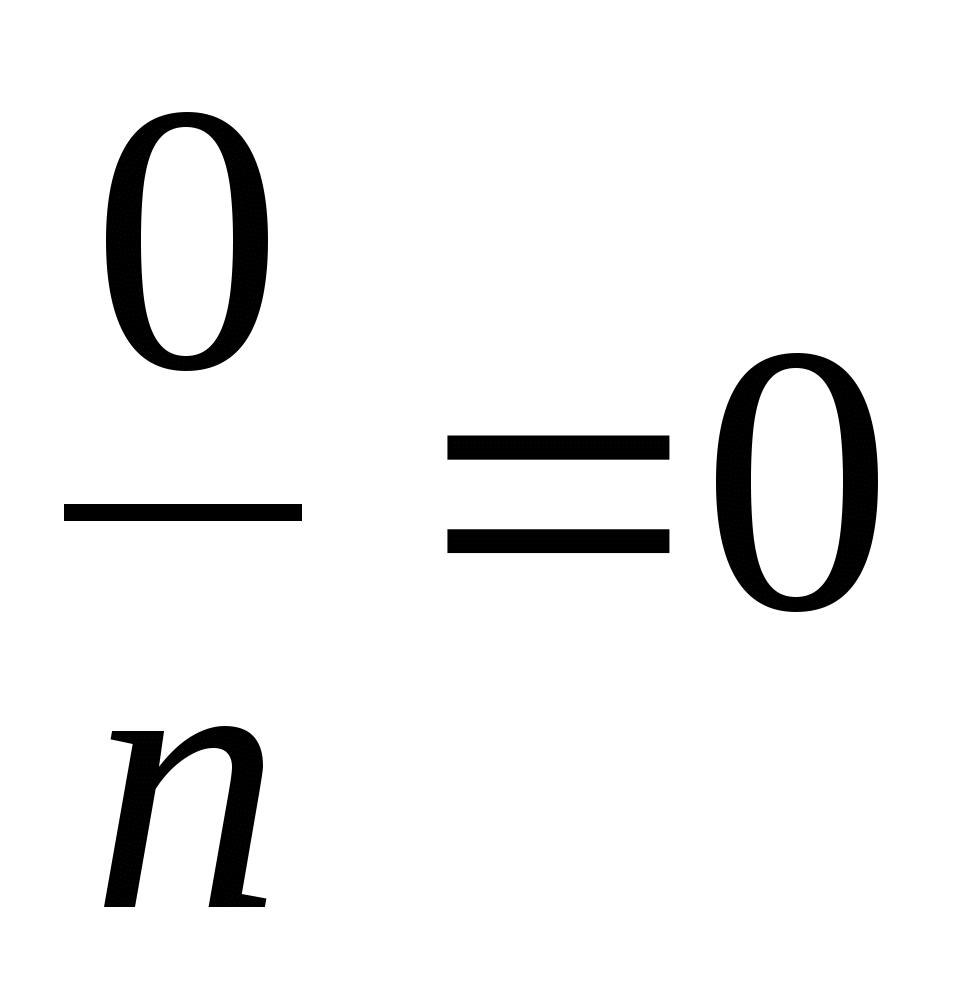
Свойство деления суммы на число

Свойство деления на 1

Свойство деления числа на себя

Свойство деления нуля на число

aⁿ

a² = a · a

a³ = a · a · a

Число а в степени n

Квадрат числа а

Куб числа a

a

1

2

3

4

5

6

7

8

9

10

a²

1

4

9

16

25

36

49

64

81

100

Таблица квадратов первых 10 натуральных чисел

a

1

2

3

4

5

6

7

8

9

10

a³

1

8

27

64

125

216

343

512

729

1000

Таблица кубов первых 10 натуральных чисел

S = v · t, ,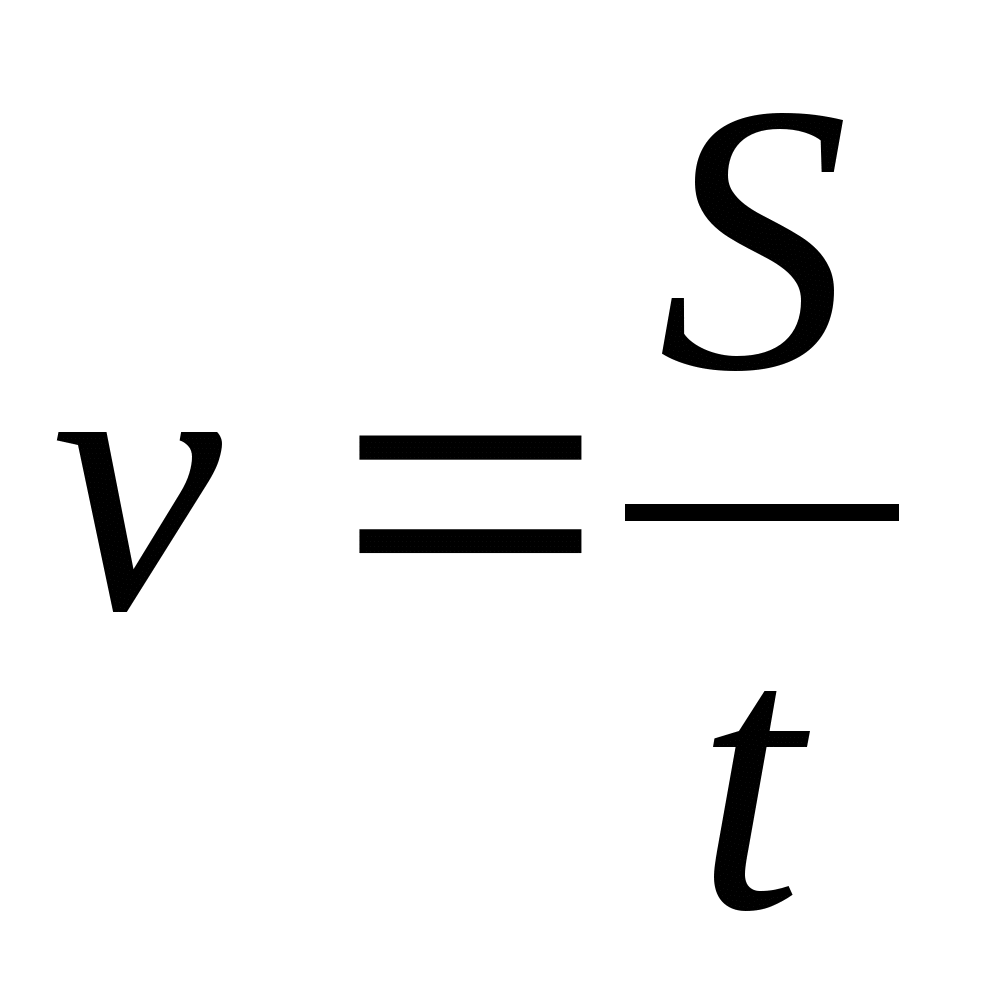

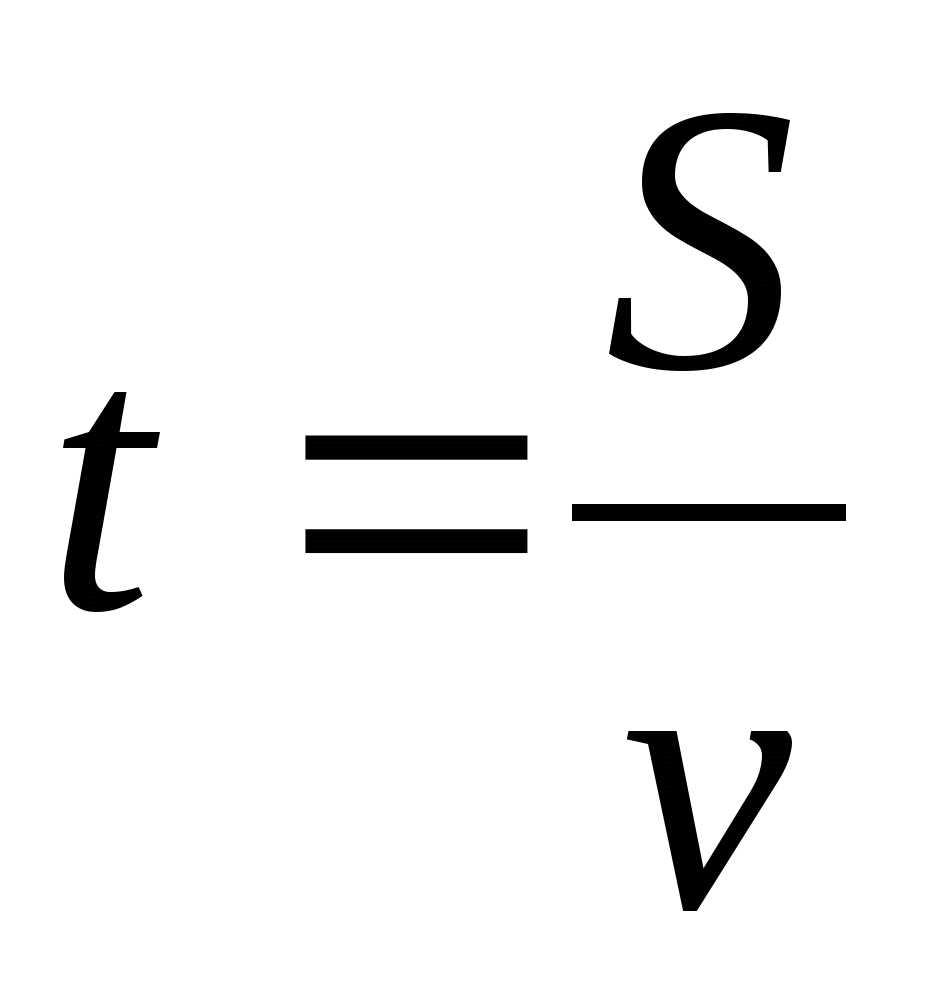
Запись правила с помощью букв – формула

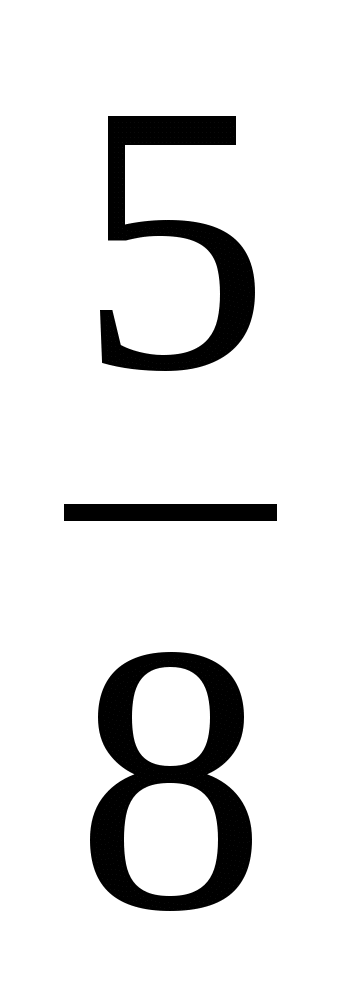
Обыкновенная дробь

5 – числитель

8 – знаменатель

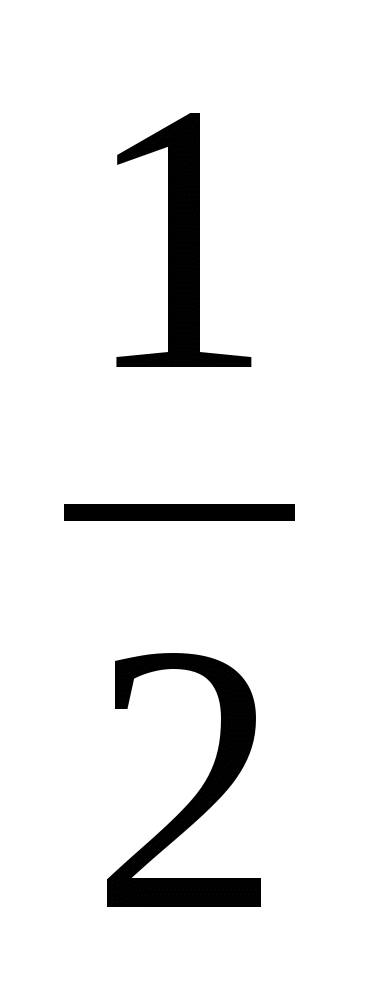
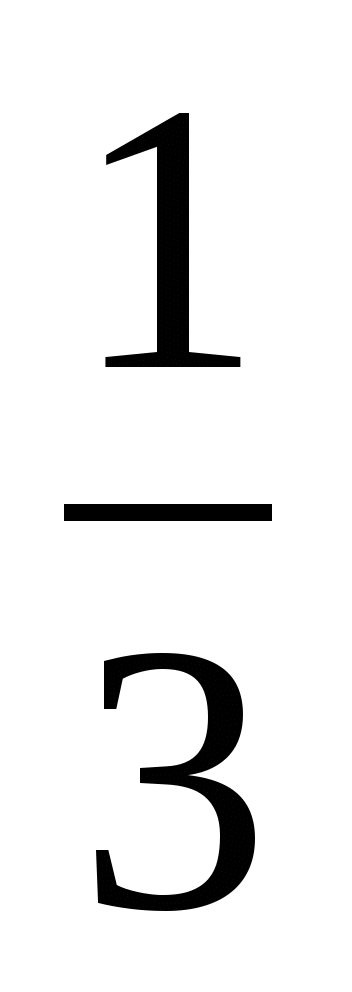
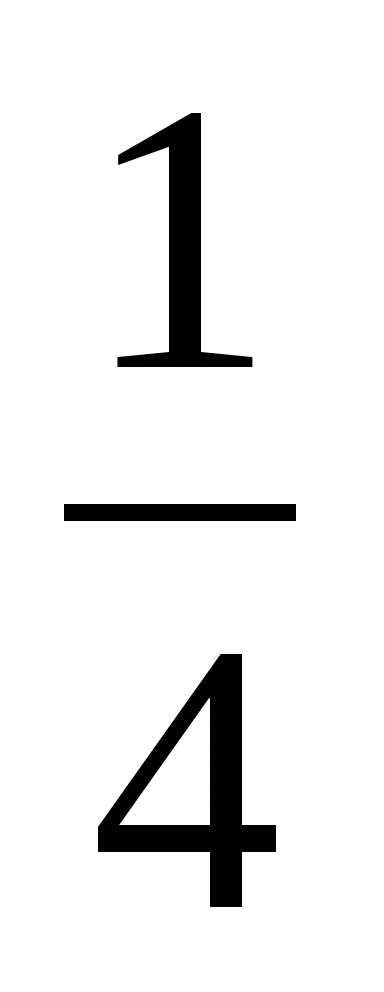
Полвина

Треть

Четверть

<

>

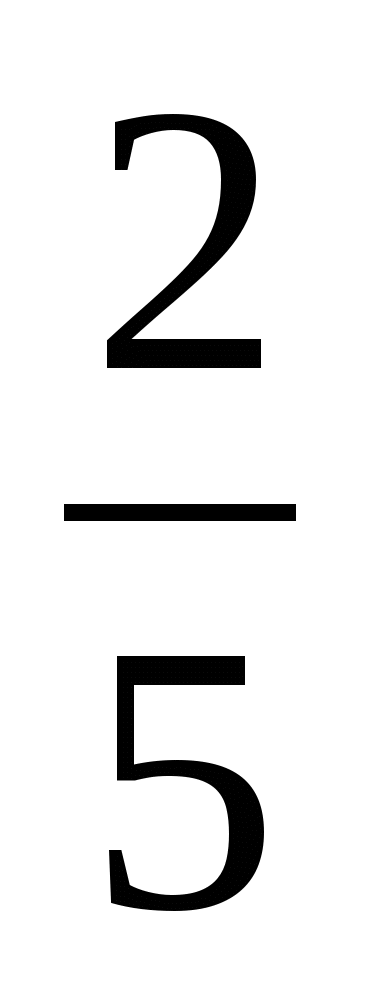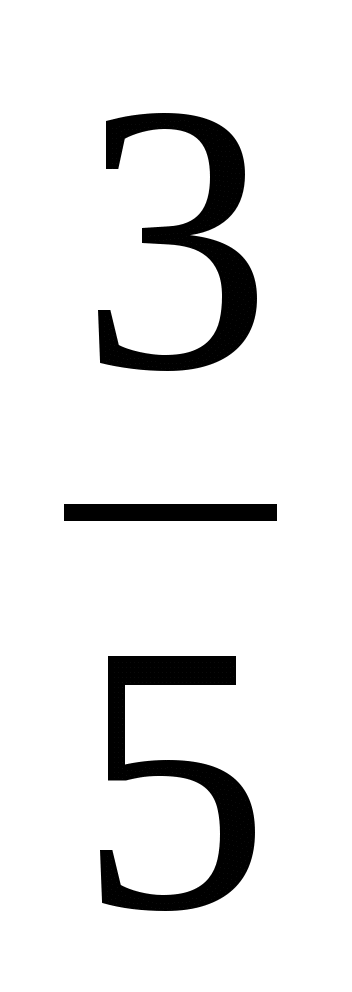
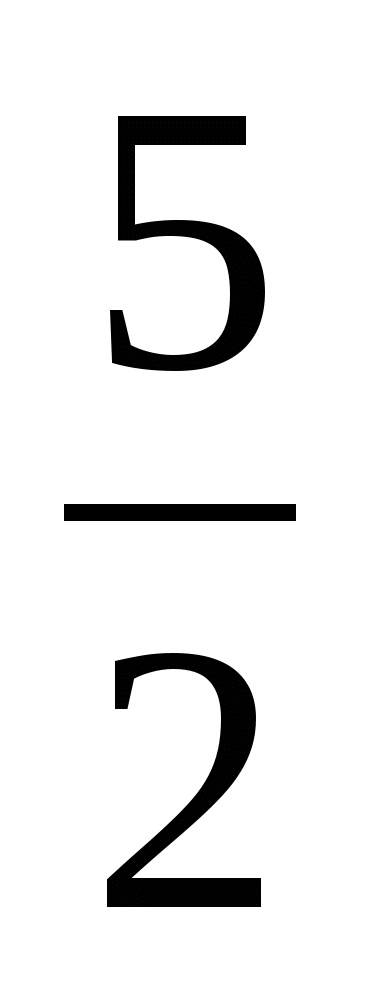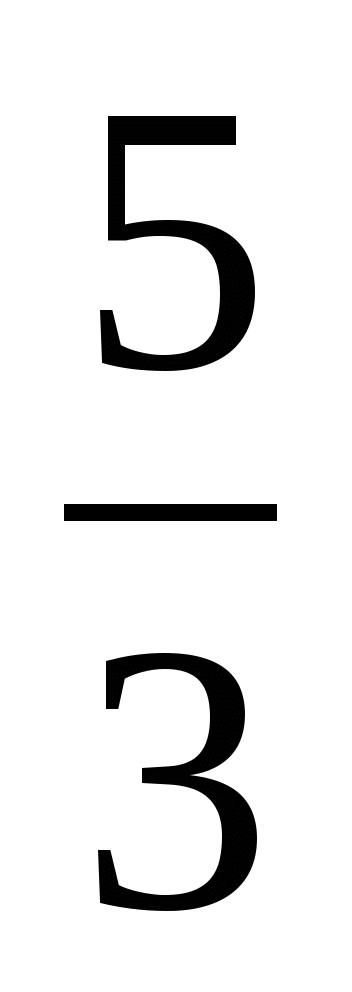
Сравнение дробей по числителю

Сравнение дробей по знаменателю

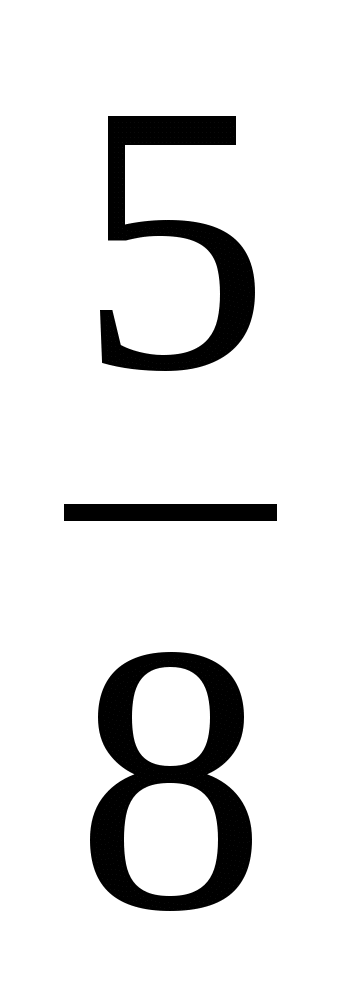, 5 < 8

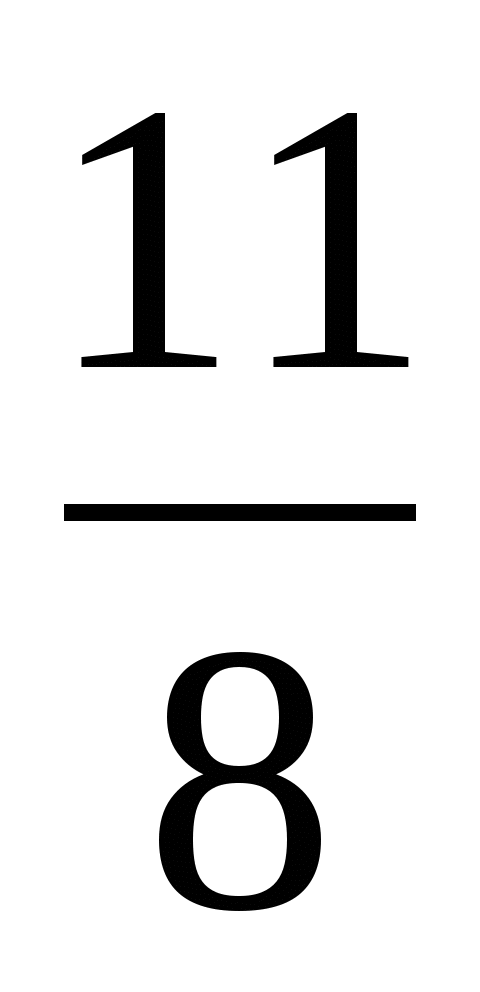, 11 > 8

Правильная дробь

Неправильная дробь

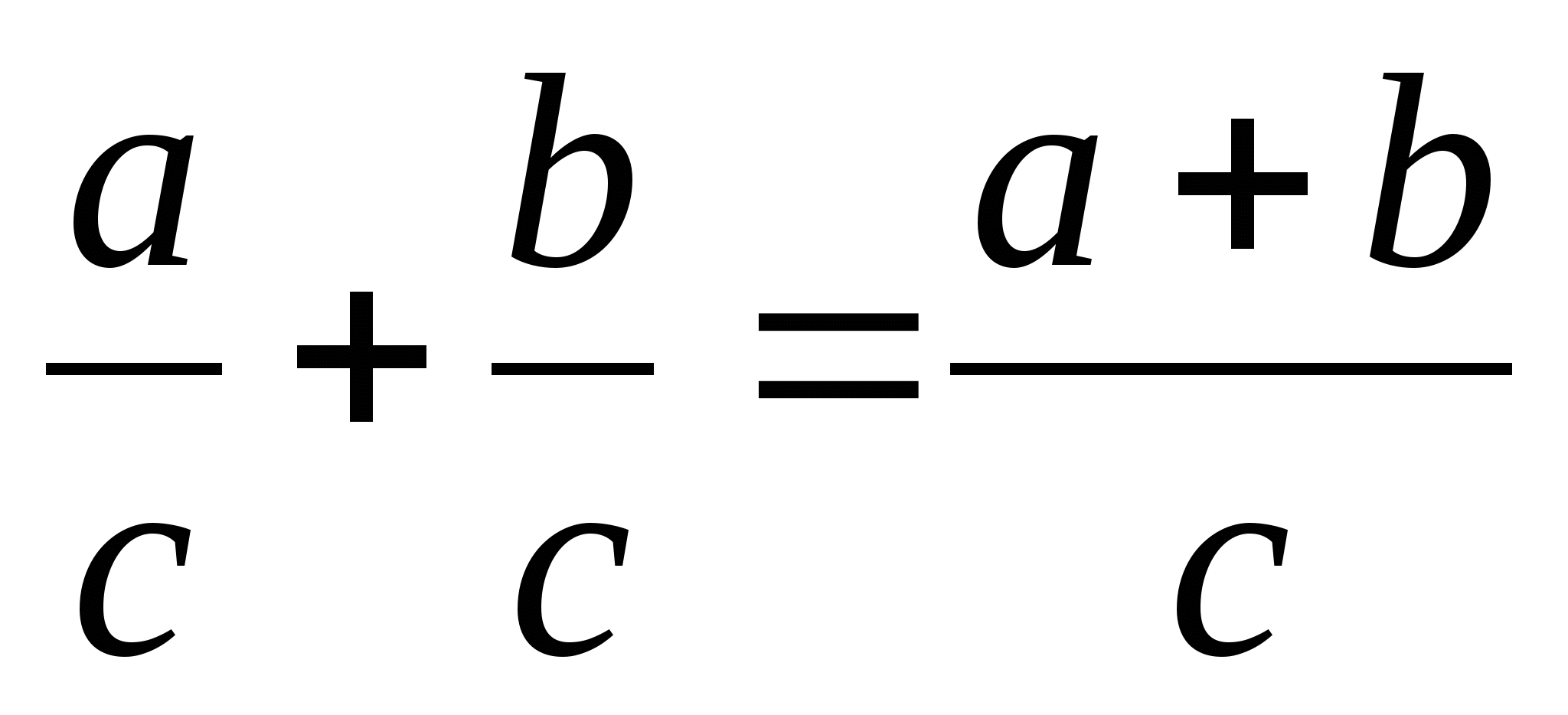
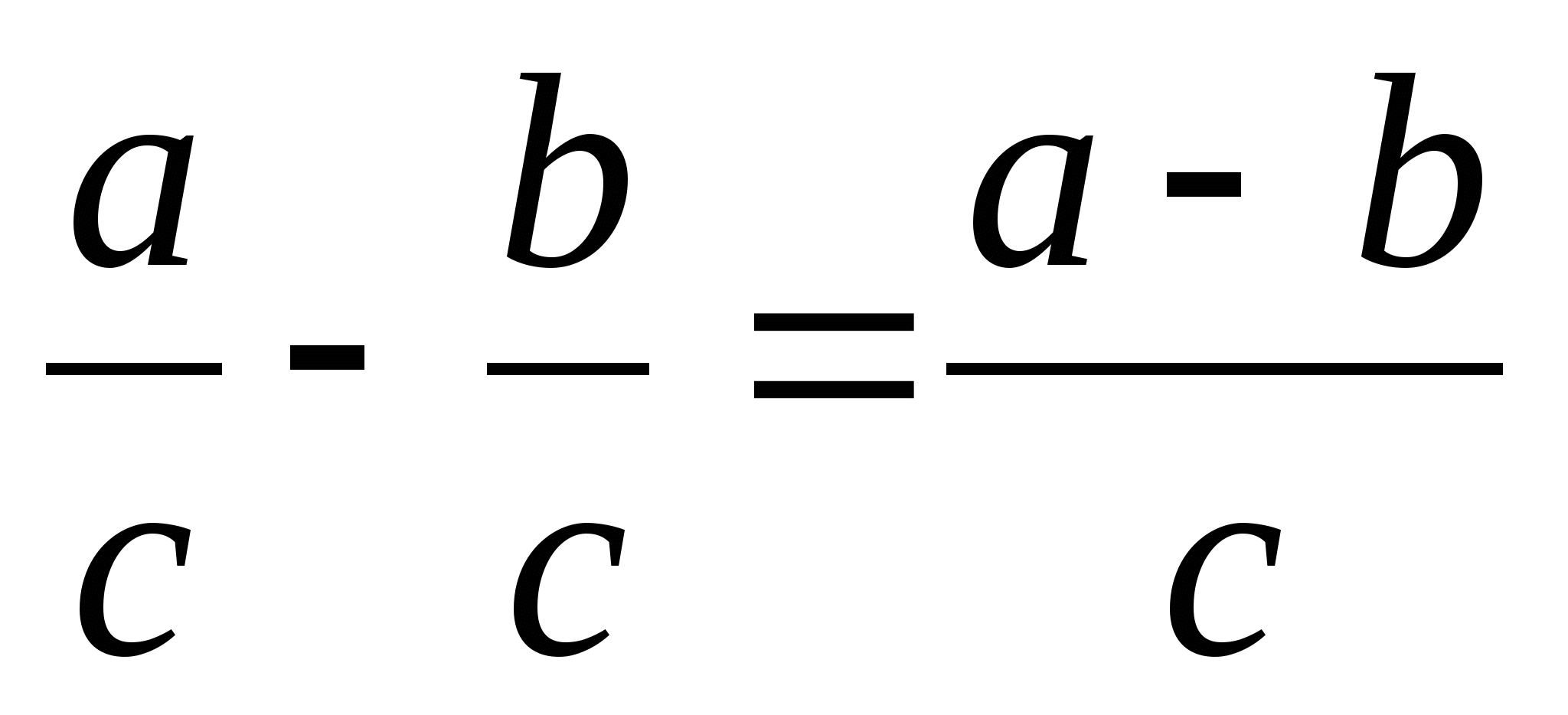
Сложение дробей с одинаковыми знаменателями

Вычитание дробей с одинаковыми знаменателями

1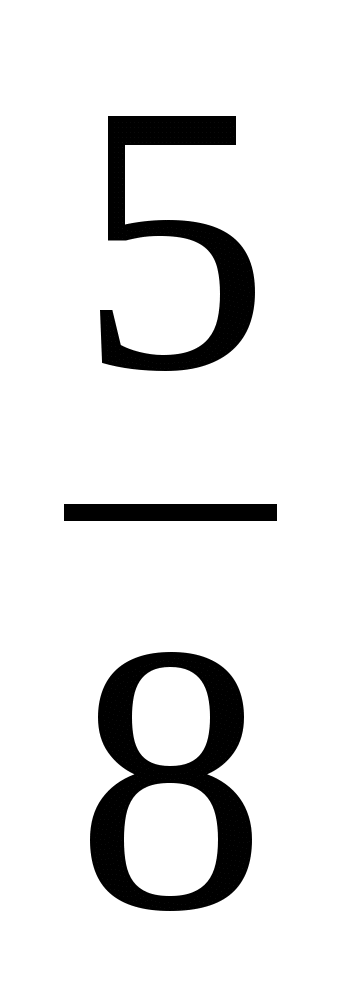

Смешанное число

1 – целая часть

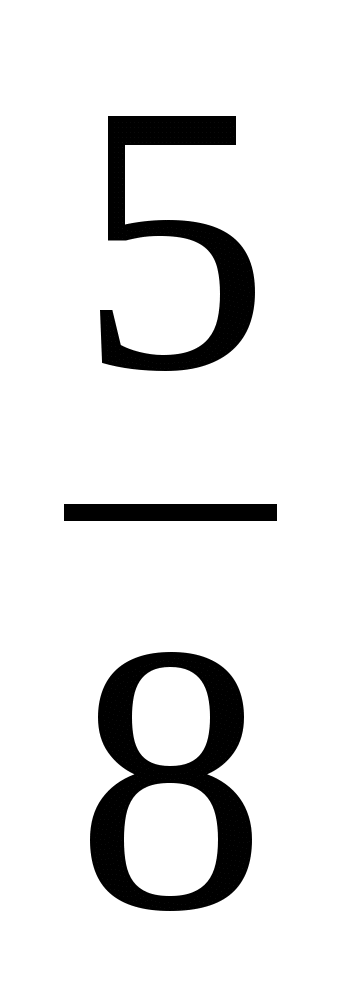— дробная часть

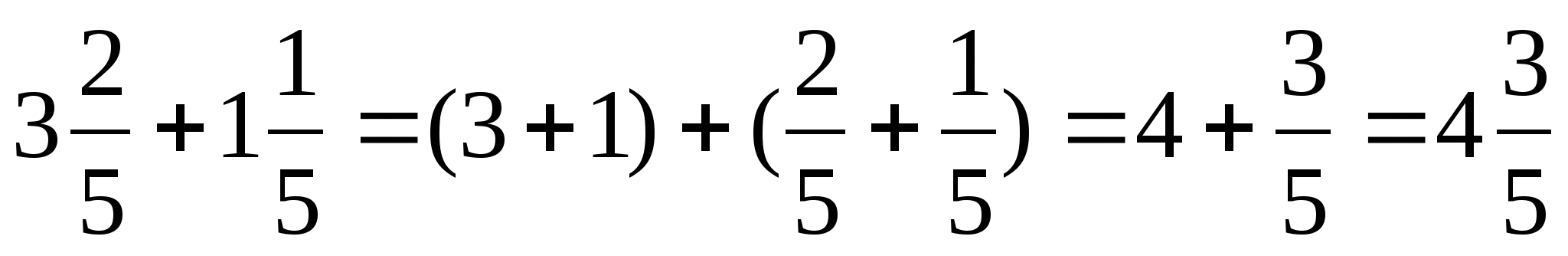
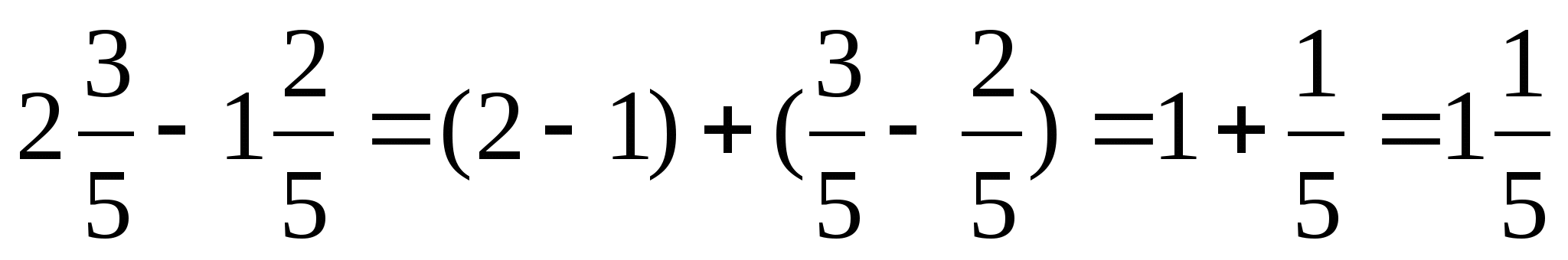
При сложении (и вычитании) чисел в смешанной записи целые части складывают (вычитают0 отдельно, а дробные – отдельно.

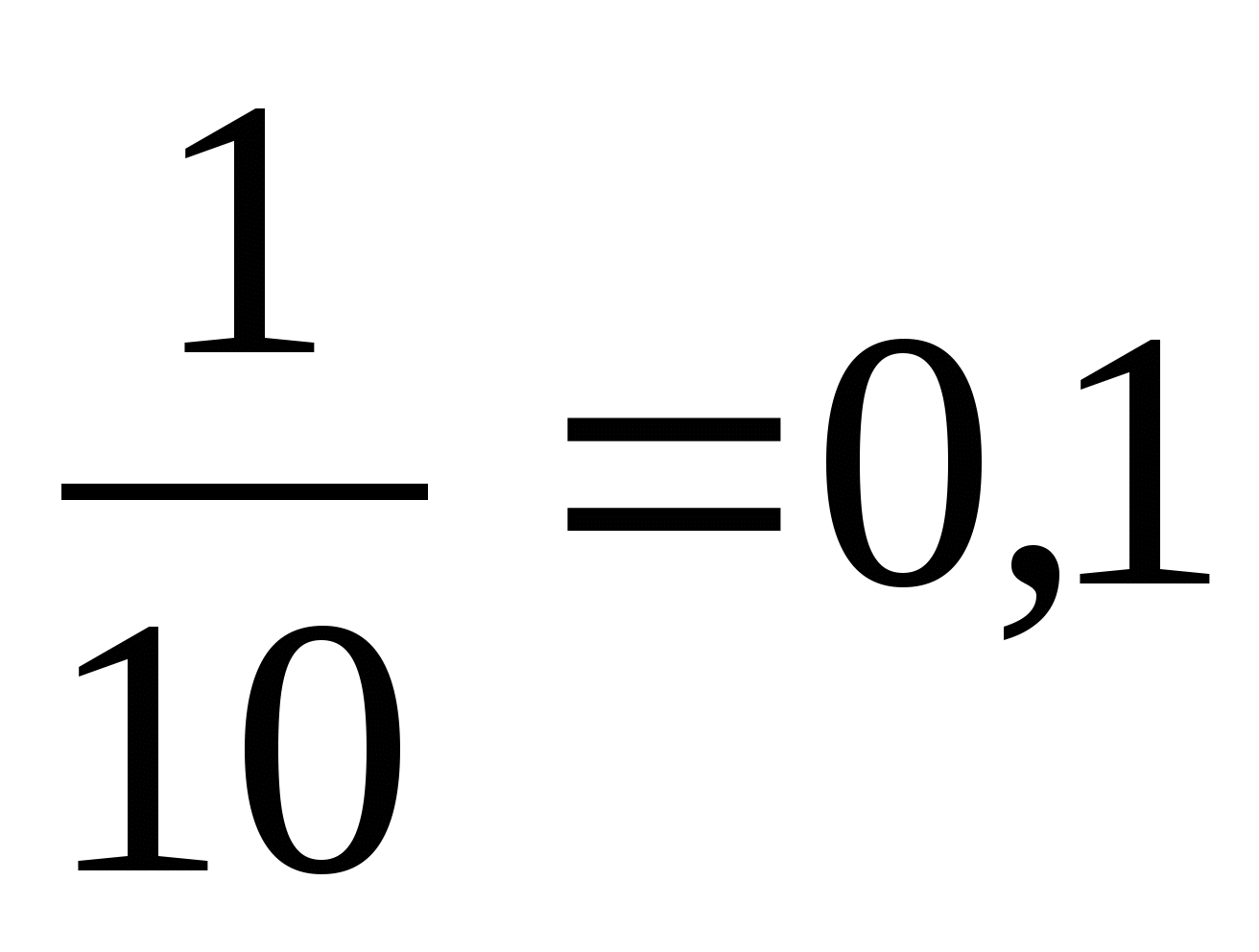
Десятичная дробь

3,700

+ 2,651

6,351

3,700

– 2,651

1,041

Сложение (вычитание) десятичных дробей

1) Уровнять в этих дробях количество знаков после запятой;

2) Записать их друг под другом так, чтобы запятая была записана под запятой;

3) Выполнить сложение (вычитание), не обращая внимание на запятую;

4) Поставить в ответе запятую под запятой в данных дробях.

86,2759 = 86,3

59,7487 = 59,7

Округление десятичных дробей

Если первая отброшенная или замененная нулем цифра равна 5, 6, 7, 8 или 9, то стоящую перед ней цифру увеличивают на 1.

Если первая отброшенная или замененная нулем цифра равна 0, 1, 2, 3 или 4, то стоящую перед ней цифру оставляют без изменения.

1,83

4

7,32

Умножение дроби на натуральное число

1) Умножить ее на число, не обращая внимание на запятую;

2) В полученном произведение отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби.

0,065 · 1000 = 0065 = 65

2,9 · 1000 = 2,900 · 1000 = 2900

Умножение десятичной дроби на 10, 100, 1000 и т. д.

В дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы

4,6 · 0,1 = 0,46

52,7 · 0,01 = 0,527

4837,6 · 0,001 = 4, 8376

Умножение числа на 0,1; 0,01; 0,001 и т. д.

То же самое, что разделить число на 10, 100, 1000 и т. д. Для этого нужно перенести запятую влево на столько цифр, сколько нулей стоит перед единицей в множителе.

0,254

0,03

0,00762

Умножение двух десятичных дробей

1) Выполнить умножение, не обращая внимание на запятые;

2) Отделить запятой столько цифр, сколько их стоит после запятой в обоих множителях вместе.

19,2 | 8 |

–16 | 2,4

3 2

–3 2

0

2,88 | 4 |

–0 | 0,72

2 8

–2 8 |

8

–8

0

Деление десятичной дроби на натуральное число

1) Разделить дробь на натуральное число, не обращая внимания на запятую;

2) Поставить в частном запятую, когда кончится деление целой части.

Если целая часть меньше делителя, то частное начинается с нуля целых.

96,1 : 10 = 9,61

8,765:100 = 008,765 : 100 = 0,08765

854,9 : 1000 = 0,8549

Деление десятичной дроби на 10, 100, 1000 и т. д.

Перенести запятую на столько знаков влево, сколько нулей стоит после единице в делителе.

12,096 : 2,24 = 1209,6 : 224 = 5,4

1209,6 | 224 |

–1120 | 5,4

89 6

–89 6

0

Деление числа на десятичную дробь.

1) В делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;

2) После этого выполнить деление на натуральное число.

45,3 : 0,1 = 453

578,9 : 0,01 = 578,90 : 0,01 = 57890

56,87 : 0,0001 = 56,8700 : 0,0001 = 568700

Деление десятичной дроби на 0,1; 0,01; 0,001 и т. д.

Перенести в дроби запятую вправо на столько цифр, сколько в делителе стоит нулей перед единицей (т. е. умножить ее на 10, 100, 1000 и т. д.)

(4,6 + 4,6 + 5,1 + 5,1 + 5,1) : 5 = 4,9

Частное от деления суммы чисел на число слагаемых – среднее арифметическое.

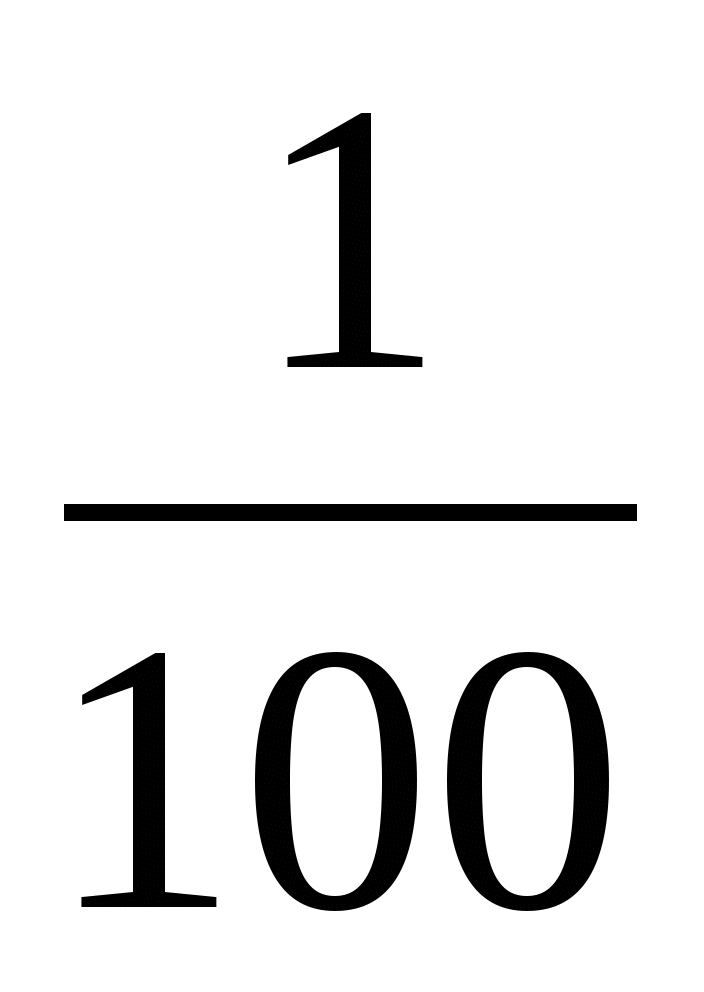часть = 1 %

0,971 = 0,971 · 100% = 97,1%

39% = 39 : 100 = 0,39

1 процент

Перевод числа в проценты

Перевод процентов в число

Начальные сведения по геометрии в курсе математики 5 класса

отрезок

А и В – концы отрезка

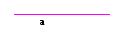
АВ – прямая

CD или а – луч

С – начало луча

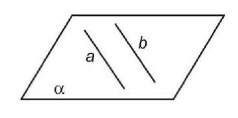
α — плоскость

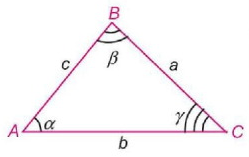
АВС – треугольник

А, В, С – вершины треугольника

АВ (с), ВС (а), АС (b) – стороны треугольника

α, β, γ – углы треугольника

P=AB+BC+AC периметр треугольника

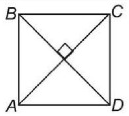
ABCD – квадрат

A, B, C, D – вершины квадрата

AB=BC=CD=DA – стороны квадрата

S=AB² площадь квадрата

Р=4·АВ периметр квадрата

ABCD – прямоугольник

A, B, C, D – вершины прямоугольника

AB=CD, BC=DA – стороны прямоугольника

S=AB·BC площадь прямоугольника

Р=2·AB+2·BC

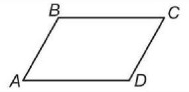
ABCD – четырехугольник

A, B, C, D – вершины четырехугольника

AB, BC, CD, DA – стороны четырехугольника

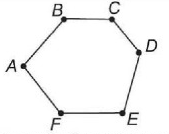
ABCDFE – многоугольник

A, B, C, D, F, E – вершины многоугольника

AB, … , FA – стороны многоугольника

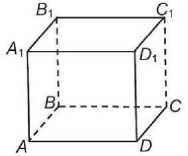
A-C₁ – куб

AB=BC=CD=DA=AA₁=…=D₁A₁ – ребра куба

V=AB³ – объем куба

A-C₁ – прямоугольный параллелипипед

AB=CD=A₁B₁=C₁D₁, BC=DA=B₁C₁=D₁A₁, AA₁=BB₁=CC₁=DD₁ – ребра прямоугольного параллелипипеда

V=AB·BC·AA₁ – объем прямоугольного параллелипипеда

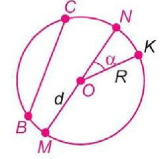
Окр (O, R) – окружность

О – центр окружности

R=ОК=ON=OM – радиус окружности

R=½d

MN=d=2·R – диаметр окружности

BC – хорда окружности

Круг

О – центр круга

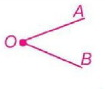
AOB – угол

О – вершина угла

АО, ОВ – стороны угла

Урок по математике в 5 классе на тему: «Как устроены таблицы»

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа № 26 ст.Должанская

МО Ейский район

Конспект урока по теме:

«Как устроены таблицы»

5 класс

УМК «Сфера»

Учитель математики

Недилько Ольга Александровна

2015 г

Тема: Как устроены таблицы

Цели урока:

Образовательные:

• Сформировать представление о таблице как очень удобной форме представления информации;

• Сформировать умение и навыки решения логических задач с помощью таблиц;

Развивающие:

• развитие логического мышления учащихся, умения сопоставлять, анализировать, делать выводы.

Воспитательные:

• Воспитывать аккуратность, внимательность, формирование познавательного интереса к предмету

Основные понятия:

Тип урока: формирование новых знаний, умений и навыков

Оборудование:

• мультимедийный проектор, карточки с заданиями для работы в парах, карточки для рефлексии.

Ход урока.

1. Организационный момент (приветствие, проверка подготовки учащихся к уроку)

2. Устная работа.

На экране с помощью мультимедийного проектора детям предлагается кроссворд по предыдущим темам. Ключевое слово — таблица – определяет тему урока.

1. 1. Назовите делитель числа 100. (десять)

   2. Какую форму имели гробницы фараонов в Древнем Египте? (пирамида)

   3. Это прямоугольный параллелепипед, у которого все стороны равны. (куб)

   4. Как называется дробь, у которой числитель меньше, чем знаменатель? (правильная)

   5. Если целое разделить на три равные части. На четыре, на пять равных частей то получатся …..(доли)

   6. Все точки окружности находятся на одинаковом расстоянии от одной точки. Как называется эта точка? (центр)

   7. Как называется число, имеющее более двух делителей? (составное)

— Какое слово получилось? (таблица) Мы к этому слову еще вернемся.

3. Сообщение темы и цели урока

— Обратите внимание на доску.

— Прочитайте текст и ответьте на вопросы:

— У Мухина по литературе оценка за год – «3». У Алексеевой по математике оценка за год – «5». У Дроздова по природоведению оценка за год – «5». У Галкина по природоведению оценка за год – « 5». У Прозоровой оценка по литературе за год — «5». У Радугиной по математике оценка за год «4». У Алексеевой по природоведению оценка за год – «4». У Алексеевой по русскому языку оценка за год – «3». ( дети читают текст и затрудняются быстро ответить на вопросы)

1) Об оценках скольких учеников говорится в тексте? (6)

2) По каким предметам приведены годовые оценки? (4)

3) Сколько учеников имеют только отличные оценки?

— В какой форме можно представить данную информацию, чтобы быстро ответить на все вопросы? (в табличной форме)

— Вы догадались, о чем пойдет речь на уроке? (О таблицах.)

Тема урока: «Как устроены таблицы».

— Какую цель мы наметим? (узнать как можно больше о таблицах, их использовании; как представляют информацию в виде таблиц)

4. Объяснение темы

Ежедневно нам необходима разнообразная информация. Она может быть представлена в самых разных формах. Одним из наиболее частых и привычных способов представления информации являются таблицы.

— Где вы в жизни встречаетесь с таблицами? Учащиеся приводят свои примеры

На экране выводятся примеры таблиц.

Действительно, таблицу мы встречаем в общешкольное расписание, календарь погоды, таблица умножения, таблица Менделеева, вышивка крестиком, игра «Морской бой».

— А теперь рассмотрим как устроена таблица:

У каждой таблицы есть общий заголовок, в котором отображается название таблицы. Каждая таблица содержит свои заголовки: это верхний заголовок и боковой заголовок. Таблица состоит из строк, их еще называют графами (по горизонтали) и столбцов (по вертикали). На пересечении строк и столбцов образуются ячейки. Каждая ячейка имеет адрес. Именно в ячейках таблиц мы храним все данные, которые заносим в таблицу. Он состоит из имени строки и столбца. Обязательно таблица должна иметь название.

— Давайте немножко поиграем, внимание на экран. Там где загорается смайлик, вы должны сказать мне адрес этой ячейки, за правильный ответ вы получите смайлики.

5. Закрепление материала.

1. Выполним №723в учебнике с.206

Используя таблицу, ответьте на вопросы:

а) В каком месяце было больше всего ясных дней?

б) В каких месяцах было одинаковое число пасмурных дней?

в) Сколько всего пасмурных дней было за четыре месяца?

г) Сколько ясных дней было за всю зиму?

Физминутка.

(Ученики повторяют движения за учителем)

Раз – подняться, подтянуться,

Два – согнуться, разогнуться,

Три – в ладоши три хлопка,

Головою три кивка.

На четыре – руки шире.

Пять – руками помахать,

Шесть – за парты сесть опять.

2. Заполнение таблицы позволяет нам решать логические задачи.

Задача «Летние каникулы». Четверо друзей – Алик, Володя, Миша и Юра – собрались в доме у Миши. Мальчики оживленно беседовали о том, как они провели лето.

— Ну, Балашов, ты, наконец, научился плавать? – спросил Володя.

— О, еще как, — ответил Балашов, — могу теперь потягаться в плавании с тобой и Аликом.

— Посмотрите, какой я гербарий собрал, — сказал Петров, прерывая разговор друзей, и достал из шкафа большую папку.

Всем, особенно Лунину и Алику, гербарий очень понравился. А Симонов обещал показать товарищам собственную им коллекцию минералов. Назовите имя и фамилию каждого мальчика.

Решение. Составим таблицу, где заголовки строк – это фамилии друзей, заголовки столбцов – их имена.

Фамилия

Имена

Алик

Володя

Миша

Юра

Балашов

—

—

—

+

Петров

—

—

+

—

Лунин

—

+

—

—

Симонов

+

—

—

—

То, что Балашов разговаривает с Володей, позволяет поставить минус в ячейке, расположенной на пересечении строки «Балашов» и столбца «Володя». Т.к. Балашов упоминает в разговоре Алика, то ставим минус в ячейке, расположенной на пересечении строки «Балашов» и столбца «Алик». Из того, что ребята собрались в доме у Миши, а Петров стал им демонстрировать свой гербарий, находящийся в шкафу, следует, что Миша и есть Петров. Это позволяет поставить плюс в ячейке, расположенной на пересечении строки «Петров» и столбца «Миша», а также заполнить минусами все пустые клетки в строке «Петров» и столбце «Миша». Гербарий понравился Лунину и Алику, значит, это два разных человека, след-но, можно поставить минус в ячейке, расположенной на пересечении строки «Лунин» и столбца «Алик».

Из первой строки таблицы следует, что фамилия Юры – Балашов (ставим плюс в соответствующей ячейке и минусы во всех свободных ячейках столбца «Юра»). Из первого столбца таблицы следует, что фамилия Алика – Симонов (ставим плюс в соответствующей ячейке и минусы во всех свободных ячейках строки «Симонов»). Единственная пустая ячейка на пересечении строки «Лунин и столбца «Володя» говорит о том, что фамилия Володи – Лунин. Таким образом, фамилия Алика – Симонов, Володи – Лунин, Миши – Петров и Юры – Балашов.

5. Самостоятельная работа.

Решение задачи в парах

Табличный способ решения логических задач

Миша не умеет плавать и никогда не играл в волейбол. А Аня заняла в прошлом году первое место по плаванию среди девочек. Оля не играет в футбол. Определите какую спортивную секцию посещает каждый из учеников?

Ученик

Спортивная секция

Волейбол

Футбол

Плавание

Миша

—

+

—

Оля

+

—

—

Аня

—

—

+

5. Итоги урока.

5. Зачем нужны таблицы?

( Для краткой записи большого числа данных

Для большей наглядности — логические задачи

Когда мы использем большой объем информации, особенно когда вы станете большими боссами

Для удобства обработки информации;)

— Как можно использовать таблицы в быту? (В качестве календаря, таблицы роста ребенка, таблицы переключения скоростей в автомобиле, таблице веса продуктов)

Домашнее задание У. п.43 №724, в газетах, журналах найти турнирные таблицы.

8. Рефлексия

-А теперь прошу определить свое настроение!

Если вы довольны своей работой на уроке и у вас все получилось, передайте зеленое облачко, если вы немного смущались и не все получалось, может вы что-то не поняли, передайте голубое облачко, если вам вообще ничего не было понятно, было трудно ,передайте с задней парты на первую парту красное облако.

Литература и источники:

• Босова Л.Л. Информатика: учебник для 5 класса.

• Е.А. Бунимович, Г.В. Дорофеев, С.Б.Суворова и др. Математика. Арифметика. Геометрия. 5 класс: учеб. для общеобразоват. организаций с прил. на электрон. носителе; издательство «Просвещение», 2014г

• Босова Л.Л. Уроки информатики в 5-6 классах: методическое пособие 2008г

• 4 .www.wikipedia.ru

• 5 .www.school.xvatit.com

Опорная таблица по курсу математики 5 класса — К уроку — Математика, алгебра, геометрия

Опорная таблица
по курсу математики 5 класса.

Начальные сведения
по геометрии в курсе математики 5 класса

Рабочая программа по математике для 5 класса (ФГОС).

Рабочая программа по математике для 5 класса.

Пояснительная записка.

Рабочая программа по математике для 5 класса разработана на основе Фундаментального ядра содержания общего образования с учётом требований к результатам освоения образовательной программы основного общего образования, представленных в федеральном государственном образовательном стандарте, утверждённом приказом Министерства образования и науки Российской Федерации от «17» декабря 2010 г. № 1897, в соответствии с авторской программой « Математика: программы: 5-11 классы. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир и др.- М.: Вентана-Граф, 2015.»

УМК:

1. Математика: 5 класс: учебник для учащихся общеобразовательных учреждений. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.- М.: Вентана-Граф, 2015.

2. Математика: 5 класс: дидактические материалы: сборник задач и контрольных работ. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.- М.: Вентана-Граф, 2016.

3. Математика: 5 класс: рабочая тетрадь № 1, № 2. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.- М.: Вентана-Граф, 2016.

4. Математика: 5 класс: методическое пособие. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.- М.: Вентана-Граф, 2015.

В программе учитываются основные положения программы развития и формирования УУД для основного общего образования, которые обеспечивают формирование российской гражданской идентичности, коммуникативных качеств личности, способствуют формированию ключевой компетенции- умения учиться.

Курс математики является фундаментом для математического образования и развития школьников, построен с учётом соотношения новых и ранее усвоенных знаний, возрастных и индивидуальных особенностей усвоения знаний учащимися. Практическая значимость курса состоит в том, что предметом его изучения являются пространственные формы и количественные отношения реального мира. В современном обществе математическая подготовка необходима каждому человеку, так как математика присутствует во всех сферах человеческой деятельности.

Цели изучения математики в 5 классе:

— развитие мышления,

— формирование абстрактного мышления,

— овладение приёмами решения задач повышенной сложности,

— учить планировать свою деятельность, критически её оценивать, принимать самостоятельные решения, отстаивать свою точку зрения,

— вырабатывать навык правильного оформления математических записей, использовать математический язык,

— развивать грамотную устную и письменную речь,

— познакомить с историей развития математики.

Место предмета в федеральном базисном учебном плане— предмет преподаётся в объёме 5 часов в неделю. Всего 5* 35 = 175 часов. В том числе 10 контрольных работ.

Формы промежуточной и итоговой аттестации— тесты, контрольные и самостоятельные работы.

Уровень обучения — базовый.

Личностные, метапредметные и предметные

результаты освоения содержания курса математики.

Личностные:

1. воспитание российской гражданской идентичности: патриотизма, осознания вклада отечественных учёных в развитие мировой науки,

2. ответственное отношение к учению, готовность и способность к саморазвитию и самообразованию,

3. осознанный выбор и построение индивидуальной траектории образования с учётом устойчивых познавательных интересов,

4. умение контролировать процесс и результат учебной деятельности,

5. критичность мышления, инициатива, активность при решении математических задач.

Метапредметные:

1. умение самостоятельно определять цели своего обучения, ставить задачи, развивать мотивы и интересы своей познавательной деятельности,

2. умение соотносить свои действия с планируемыми результатами, контролировать и корректировать свою деятельность,

3. умения определять понятия, обобщать, устанавливать аналогии, классифицировать,

4. умение устанавливать причинно-следственные связи, логически рассуждать, делать умозаключение, выводы,

5. развитие компетентности в области использования ИКТ,

6. первоначальные представления об идеях и методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов,

7. умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни,

8. умение понимать и использовать математические средства наглядности для иллюстрации, аргументации, выдвигать гипотезы,

9. умение работать по алгоритму и понимание его сущности.

Предметные:

1. осознание значения математики для жизни человека,

2. представление о математической науке, этапах её развития, значении для развития цивилизации,

3. умение работать с текстом, выражать грамотно свои мысли с использованием математической терминологии,

4. владение базовым понятийным аппаратом по основным разделам содержания,

5. практически значимые умения и навыки: решать текстовые задачи разными способами, изображать фигуры на плоскости, измерять длины отрезков, величины углов, вычислять площади и объёмы фигур, читать графики, работать с таблицами, решать комбинаторные задачи и т. д.

Содержание курса.

Содержание курса математики в 5 классе представлено следующими разделами: «Арифметика», «Числовые и буквенные выражения. Уравнения», «Геометрические фигуры. Измерения геометрических величин», «Элементы статистики, вероятности. Комбинаторные задачи.», «Математика в историческом развитии».

Содержание раздела «Арифметика» служит базой для дальнейшего изучения математики. Развитие понятия о числе связано с изучением рациональных чисел: натуральных чисел, обыкновенных и десятичных дробей.

Натуральные числа. Ряд натуральных чисел. Десятичная запись натуральных чисел. Округление натуральных чисел. Координатный луч. Сравнение, сложение, вычитание натуральных чисел. Свойства сложения. Умножение и деление натуральных чисел. Свойства умножения. Деление с остатком. Степень с натуральным показателем, решение текстовых задач арифметическими способами.

Дроби. Обыкновенные дроби. Основное свойство дроби. Правильные и неправильные дроби. Смешанные числа. Сравнение, сложение, вычитание обыкновенных дробей и смешанных чисел. Десятичные дроби. Сравнение, округление, сложение, вычитание десятичных дробей. Прикидки результатов. Представление десятичной дроби в виде обыкновенной и наоборот. Проценты. Нахождение процентов от числа. Нахождение числа по его процентам. Решение текстовых задач арифметическими способами.

Величины. Зависимости между величинами. Единицы длины, площади, объёма, массы, времени, скорости. Представление зависимостей в виде формул, вычисления по формулам.

Числовые и буквенные выражения. Уравнения. Числовые выражения и их значение. Порядок действий в числовых выражениях. Буквенные выражения. Раскрытие скобок. Подобные слагаемые, приведение подобных слагаемых, формулы. Уравнение. Корень уравнения. Свойства уравнений. Решение текстовых задач с помощью уравнений.

Геометрические фигуры. Измерения геометрических величин. Отрезок. Построение отрезка. Длина отрезка, ломаной. Измерение длины отрезка. Периметр многоугольника. Плоскость. Прямая. Луч. Угол. Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира. Прямоугольник. Квадрат. Треугольник. Виды треугольников. Площадь прямоугольника и квадрата. Ось симметрии фигуры. Прямоугольный параллелепипед, куб, пирамида. Объём прямоугольного параллелепипеда и куба.

Элементы статистики, вероятности. Комбинаторные задачи. Представление данных в виде таблиц, круговых и столбчатых диаграмм, графиков. Среднее арифметическое. Среднее значение величины. Случайное событие. Достоверное и невозможное события. Вероятность случайного события. Решение комбинаторных задач.

Математика в историческом развитии. Римская система счисления. Позиционные системы счисления. Обозначение цифр в Древней Руси. Старинные меры длины. Метрическая система мер в России, в Европе. История формирования математических символов. Дроби в Вавилоне, Египте, Риме, на Руси. Открытие десятичных дробей.

Тематическое планирование.

Формулировать и записывать с помощью формул свойства сложения и вычитания. Составлять числовые и буквенные выражения по условию задачи. Решать уравнения на основании зависимостей между компонентами действий сложения и вычитания.

Решать текстовые задачи с помощью уравнений. Распознавать на чертежах углы, треугольники, прямоугольники. Измерять и строить углы, биссектрису угла, классифицировать углы, треугольники, описывать свойства прямоугольника. Находить с помощью формул периметры прямоугольника и квадрата. Строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи. Распознавать фигуры, имеющие ось симметрии.

21-24

Сложение натуральных чисел. Свойства сложения.

4

25-28

Вычитание натуральных чисел.

4

29-31

Числовые и буквенные выражения. Формулы.

3

32

Контрольная работа № 2

1

33-35

Уравнение. Тест.

3

36-37

Угол. Обозначение углов.

2

38-42

Виды углов. Измерение углов. Тест.

5

43-44

Многоугольники. Равные фигуры.

2

45-47

Треугольник и его виды.

3

48-50

Прямоугольник. Ось симметрии фигуры.

3

51

Повторение и систематизация.

1

52

Контрольная работа № 3

1

53-88

Умножение и деление натуральных чисел.

36

Формулировать и записывать в виде формул свойства умножения и деления натуральных чисел. Решать уравнения на основе зависимостей между компонентами. Находить остаток при делении натуральных чисел. Вычислять значение степени числа. Находить с помощью формул площади прямоугольника и квадрата. Выражать одни единицы площади через другие.

Распознавать на рисунках прямоугольный параллелепипед и пирамиду, изображать их развёртки. Находить объёмы прямоугольного параллелепипеда и куба с помощью формул. Выражать одни единицы объёма через другие. Решать комбинаторные задачи.

53-56

Умножение. Переместительное свойство умножения. Тест.

4

57-59

Сочетательное и распределительное свойства умножения.

3

60-65

Деление. Тест.

6

66-68

Деление с остатком.

3

69-71

Степень числа.

3

72

Контрольная работа № 4

1

73-76

Площадь. Площадь прямоугольника. Тест.

4

77-79

Прямоугольный параллелепипед. Пирамида.

3

80-83

Объём прямоугольного параллелепипеда.

4

84-86

Комбинаторные задачи.

3

87

Повторение и систематизация.

1

88

Контрольная работа №5

1

89-105

Обыкновенные дроби.

17

Распознавать обыкновенную дробь, правильные и неправильные дроби, смешанные числа, читать их и записывать. Сравнивать, складывать и вычитать обыкновенные дроби с равными знаменателями. Преобразовывать неправильную дробь в смешанное число, смешанное число в неправильную дробь. Уметь записывать результат деления двух натуральных чисел в виде обыкновенной дроби.

89-92

Понятие обыкновенной дроби.

4

93-95

Правильные и неправильные дроби. Сравнение дробей.

3

96-97

Сложение и вычитание дробей с одинаковыми знаменателями

2

98

Дроби и деление натуральных чисел

1

99-103

Смешанные числа. Тест.

5

104

Повторение и систематизация

1

105

Контрольная работа №6

1

106-152

Десятичные дроби.

47

Распознавать, читать, записывать десятичные дроби. Называть разряды десятичных знаков в записи десятичных дробей. Сравнивать и округлять десятичные дроби. Выполнять прикидку результатов вычислений. Выполнять арифметические действия над десятичными дробями. Находить среднее арифметическое нескольких чисел. Понимать «один процент». Представлять проценты в виде десятичных дробей и десятичные дроби в виде процентов. Находить процент от числа и число по его процентам.

106-109

Представление о десятичных дробях.

4

110-112

Сравнение десятичных дробей.

3

113-114

Округление чисел. Тест. Прикидки.

2

115-121

Сложение и вычитание десятичных дробей.

7

122

Контрольная работа №7

1

123-129

Умножение десятичных дробей. Тест.

7

130-138

Деление десятичных дробей.

9

139

Контрольная работа №8

1

140-142

Среднее арифметическое. Среднее значение величины.

3

143-146

Проценты. Нахождение процентов от числа.

4

147-150

Нахождение числа по его процентам.

4

151

Повторение и систематизация.

1

152

Контрольная работа №9

1

153-175

Повторение и систематизация учебного материала.

23

153-166

Повторение

14

167

Контрольная работа

№ 10

1

168-175

Обобщение. Решение задач. Резерв.

8

Оборудование и ТСО.

1. Таблицы по математике для 5 классов.

2. Портреты выдающихся деятелей в области математики.

3. Медиаресурсы, интернет.

4. Наборы геометрических тел.

5. Комплект чертёжных инструментов.

6. Модель единицы объёма.

7. Компьютер.

8. Мультимедиапроектор.

9. Экран.

10. Интерактивная доска.

Литература.

1. Нормативные документы.

Федеральный государственный образовательный стандарт основного общего образования.

Примерные программы основного общего образования. Математика. (Стандарты второго поколения.)- М.: Просвещение, 2010.

Формирование универсальных учебных действий в основной школе: система заданий. А.Г Асмолов, О.А.Карабанова.- М.:просвещение,2010.

2. УМК А.Г. Мерзляк. В.Б.Полонский, М.С. Якир. (список в начале).

3. Занимательная математика:5-11 классы. Гаврилова Т.Д.- Волгоград: Учитель,2008.

4. Нестандартные задачи по математике. Левитас Г.Г. -М. : ИЛЕКСА, 2007.

5. Математические олимпиады в школе: 5-11 классы. Фарков А.В. — М.: Айрис-Пресс, 2005.

Рабочая программа по математике 5 класс ФГОС

п/п

Кол-во

часов

Тема урока

Обязательный

минимум

содержания

основной

образовательной

программы(дидактические единицы)

Формируемые умения

/личностные качества

(планируемые результаты обучения)

Виды деятельности учащихся, форма работы

Дата проведения

Предметные умения

(базовые

понятия)

Универсальные

Учебные

действия(УУД)

план

факт

Глава I. НАТУРАЛЬНЫЕ ЧИСЛА (53 ч)

1

Десятичная

Система

счисления

Римские цифры, сумма разрядных слагаемых, позиционный способ записи числа, десятичная система счисления

Формирование представлений учащихся

о математике как о

методе познания действительности

Коммуникативные: развить у учащихся представление о месте математики в системе наук. Регулятивные: формировать целевые установки учебной деятельности.

Познавательные: различать методы познания окружающего мира по его целям (наблюдение, опыт, эксперимент, моделирование, вычисление)

ФО

ИРД

ИРК

1

Десятичная

система

счисления

Римские цифры, сумма разрядных слагаемых, позиционный способ записи числа, десятичная система счисления

Научиться читать, записывать числа натурального ряда и

ноль с помощью

арабских цифр и в простейших случаях с помощью римских цифр

Коммуникативные: развивать умение

точно и грамотно выражать свои мысли, отстаивать свою точку зрения в процессе дискуссии.

Регулятивные: определять новый уровень отношения к самому себе как субъекту деятельности.

Познавательные: анализировать результаты элементарных исследований, фиксировать их результаты

ФО

ДСР

(С-1.1)

1

Десятичная

Система

счисления

Римские цифры, сумма разрядных слагаемых, позиционный способ записи числа, десятичная система счисления

Научиться называть предшествующее, последующее число, числа, расположенные между двумя данными натуральными числами

Коммуникативные: формировать коммуникативные действия, направленные

на структурирование информации по данной теме.

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий.

Познавательные: выявлять особенности (качества, признаки) разных объектов в процессе их рассматривания

ФО

ДСР

(С- 1.2)

1

Десятичная

Система

счисления

Римские цифры, сумма разрядных слагаемых, позиционный способ записи числа, десятичная система счисления

Обобщить знания, умения по теме

« Десятичная система счисления»

Коммуникативные: формировать коммуникативные действия, направленные

на структурирование информации по данной теме.

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий.

Познавательные: выявлять особенности (качества, признаки) разных объектов в процессе их рассматривания

1

Числовые и буквенные выражения

Буквенные выражения, значение буквенных выражений, числовые выражения, значение числовых выражений, математический язык

Научиться различать числовые и буквенные выражения, находить значения числовых выражений

Коммуникативные: формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы.

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий.

Познавательные: сопоставлять характеристики объектов по одному или нескольким признакам, выявлять сходства и различия объектов

ФО

ИРД

1

Числовые и буквенные выражения

Буквенные выражения, значение буквенных выражений, числовые выражения, значение числовых выражений, математический язык

Научиться составлять числовое (буквенное) выражение по тексту задачи, объяснять смысл данного выражения, опираясь на текст задачи

Коммуникативные: воспринимать текст с учетом поставленной учебной задачи, находить в тексте информацию, необходимую для ее решения.

Регулятивные: самостоятельно находить и формулировать учебную проблему, составлять план выполнения работы.

Познавательные: выполнять учебные задачи, не имеющие однозначного решения

ФО

ДСР

(С- 2.1)

1

Числовые и буквенные выражения

Буквенные выражения, значение буквенных выражений, числовые выражения, значение числовых выражений, математический язык

Обобщить знания, умения по теме «Числовые и буквенные выражения»

Коммуникативные: управлять своим поведением (контроль, самокоррекция, оценка своего действия).

Регулятивные: осознавать самого себя как движущую силу своего научения, формировать способность к мобилизации сил и энергии, к волевому усилию — выбору в ситуации мотивационного конфликта и к преодолению препятствий.

Познавательные: произвольно и осознанно владеть общим приемом решения задач

ФО

ДСР

(С- 2.2)

1

Язык геометрических рисунков

Геометрический рисунок. Чтение геометрического рисунка. Построение геометрического рисунка по описанию.

Научиться правильно обозначать точки, отрезки, прямые на чертежах

Коммуникативные: способствовать формированию научного мировоззрения.

Регулятивные: оценивать весомость приводимых доказательств и рассуждений.

Познавательные: осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края

ФО

ИРД

ИРК

1

Язык геометрических рисунков

Геометрический рисунок. Чтение геометрического рисунка. Построение геометрического рисунка по описанию.

Научиться выполнять геометрические рисунки по описанию

Коммуникативные: развивать умение обмениваться знаниями между членами класса для принятия эффективных совместных решений.

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий.

Познавательные: выявлять особенности (качества, признаки) разных объектов в процессе их рассмотрения

ДСР

( С-3.1)

1

Входная контрольная работа

Научиться воспроизводить приобретенные знания, умения, навыки в конкретной деятельности

Коммуникативные: управлять своим поведением (контроль, самокоррекция, оценка своего действия).

Регулятивные: формировать способность к мобилизации сил и энергии, к волевому усилию — выбору в ситуации мотивационного конфликта и к преодолению препятствий.

Познавательные: ориентироваться на разнообразие способов решения задач

1

Язык геометрических рисунков

Геометрический рисунок. Чтение геометрического рисунка. Построение геометрического рисунка по описанию.

Научиться различать прямые, отрезки, треугольники, прямоугольники на чертежах и описывать варианты взаимного расположения прямых и отрезков

Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений.

Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций. Познавательные: осуществлять сравнение и классификацию по заданным критериям

ФО

ДСР

(С- 3.2)

1

Прямая.Отрезок.Луч

Основные геометрические фигуры: прямая, отрезок, луч.

Научиться правильно обозначать, называть прямые, отрезки, лучи на чертежах; находить и обозначать точки их пересечения (если таковые имеются)

Коммуникативные: слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою точку зрения.

Регулятивные: проводить контроль в форме сравнения способа действия и его результат с заданным эталоном с целью обнаружения отклонений от эталона и внесения необходимых коррективов.

Познавательные: выделять существенную информацию из текстов разных видов

ФО

ИРД

ИРК

1

Прямая.Отрезок.Луч

Основные геометрические фигуры: прямая, отрезок, луч.

Научиться делать рисунки по описанию взаимного расположения отрезков, лучей и прямых

Коммуникативные: выслушивать мнение членов команды не перебивая; принимать коллективное решение.

Регулятивные: прогнозировать результат и уровень усвоения материала; определять новый уровень отношения к самому себе как к субъекту деятельности.

Познавательные: формировать основы смыслового чтения научных и познавательных текстов

ДСР

( С-3.1)

1

Сравнение отрезков. Длина отрезка

Длина отрезка. Сравнение отрезков. Равные отрезки. Запись выражений для длины отрезков

Ввести определение равных отрезков, соотношение длин равных отрезков, обозначение равных отрезков на чертежах. Научиться применять полученные знания и умения при решении задач

Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками .

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий.

Познавательные: уметь устанавливать причинно-следственные связи

ФО

ДСР

(С-5.1)

1

Сравнение отрезков. Длина отрезка

Длина отрезка. Сравнение отрезков. Равные отрезки. Запись выражений для длины отрезков.

Научиться переводить одни единицы измерения длины в другие, записывать числовые и буквенные выражения для нахождения длины всего отрезка, если известны длины его частей

Коммуникативные: учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его.

Регулятивные: сравнивать способ действия и его результат с заданным эталоном с целью обнаружения отклонений от эталона и внесения необходимых коррективов. Познавательные: владеть общим приемом решения учебных задач

ДСР

(С-5.2)

1

Ломаная

Кривая, прямая, ломаная, вершина ломаной, звенья ломаной, самопересекаю-щаяся ломаная; компоненты произведения

Научиться различать понятия линии, отрезка, ломаной; правильно обозначать и называть ломаную, находить длину данной ломаной

Коммуникативные: воспринимать текст с учетом поставленной учебной задачи, находить в тексте информацию, необходимую для ее решения.

Регулятивные: определять новый уровень отношения к самому себе как субъекту деятельности.

Познавательные: осуществлять выбор наиболее эффективных способов решения задач

ФО

ИРД

1

Ломаная

Кривая, прямая, ломаная, вершина ломаной, звенья ломаной, самопересекаю-щаяся ломаная; компоненты произведения

Научиться различать замкнутые, незамкнутые, самопересекающиеся ломаные; строить указанные ломаные по описанию. Составлять числовое или буквенное выражение для нахождения длины ломаной

Коммуникативные: управлять своим поведением (контроль, самокоррекция, оценка своего действия).

Регулятивные: осознавать уровень и качество усвоения знаний и умений.

Познавательные: выявлять особенности (качества, признаки) разных объектов в процессе их рассматривания

ДСР

(С-6.1)

1

Координатный луч

Координатный луч, начало отсчета, единичный отрезок

Научиться отличать координатный луч от обычного луча, строить точки с указанными координатами на координатном луче, выбрав удобный единичный отрезок, находить координаты имеющихся точек

Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками.

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий.

Познавательные: уметь осуществлять анализ объектов с выделением существенных и несущественных признаков

ФО

ДСР

(С-7.1)

1

Координатный луч

Координатный луч, начало отсчета, единичный отрезок

Систематизировать знания и умения учащихся по теме «Координатный луч, прямая, отрезок, ломаная»

Коммуникативные: формировать коммуникативные действия, направленные на структурирование информации по данной теме. Регулятивные: находить и формулировать учебную проблему, составлять план выполнения работы.

Познавательные: уметь осуществлять выбор наиболее эффективных способов решения образовательных задач в зависимости от конкретных условий

Т №1

1

Контрольная работа № 1 по теме «Сравнение натуральных чисел, прямая, отрезок, ломаная, координатный луч»

Натуральные числа. Отрезок,

ломаная, луч.

Научиться воспроизводить приобретенные знания, умения, навыки в конкретной деятельности

Коммуникативные: управлять своим поведением (контроль, самокоррекция, оценка своего действия).

Регулятивные: формировать способность к мобилизации сил и энергии, к волевому усилию — выбору в ситуации мотивационного конфликта и к преодолению препятствий.

Познавательные: ориентироваться на разнообразие способов решения задач

КР№1

1

Решение практических расчётных задач.

Решение практических расчётных задач.

Расширить представления о практическом применении математики

Коммуникативные: учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его.

Регулятивные: сравнивать способ действия и его результат с заданным эталоном с целью обнаружения отклонений от эталона внесения необходимых коррективов.

Познавательные: произвольно и осознанно владеть общим приемом решения задач

1

Округление натуральных чисел

Точное значение величины, приближенное значение величины, округление, правило округления чисел

Вывести правило округления натуральных чисел и научиться применять его в практической деятельности

Коммуникативные: уметь выслушивать мнение членов команды, не перебивая; принимать коллективные решения.

Регулятивные: находить и формулировать учебную проблему, составлять план выполнения работы.

Познавательные: уметь строить рассуждения в форме связи простых суждений об объекте, его строении, свойствах и связях

ФО
ИРД

1

Округление натуральных чисел

Точное значение величины, приближенное значение величины, округление, правило округления чисел

Совершенствовать знания и умения учащихся по теме «Округление натуральных чисел»

Коммуникативные: развивать умение точно и грамотно выражать свои мысли, отстаивать свою точку зрения в процессе дискуссии. Регулятивные: формировать целевые установки учебной деятельности, выстраивать алгоритм действий.

Познавательные: уметь осуществлять анализ объектов с выделением существенных и несущественных признаков

ДСР

(С-8.1)

1

Прикидка результата

действия

Прикидка результата действия, основные способы вычислений с помощью прикидки