Теория 5 класс математика: Математика. Вся теория из учебника за 5 класс, Мерзляк – Определения и формулы метематика 5 класс Виленкин

Теоретические вопросы. Математика. 5 класс.

Свойства

Свойства сложения

1. Переместительное. Сумма не изменяется при перестановке слагаемых. a+b=b+a

2. Сочетательное. Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а затем к полученной сумме прибавить второе слагаемое. a+(b+c)=(a+b)+c

3. От прибавления нуля число не изменяется. a+0=a

Свойства вычитания

1. Свойство вычитания суммы из числа. Для того чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а затем из полученной разности ­– второе слагаемое. a−(b+c)=(a−b)−c

2. Свойство вычитания числа из суммы. Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое. (a+b)−c=(a−c)+b=a+(b−c)

3. Если из числа вычесть нуль, оно не изменится. a–0=a

4. Если из числа вычесть это число, получится нуль. a–а=0

Свойства умножения

1. Переместительное. Произведение двух чисел не изменяется при перестановке множителей. a·b=b·a

2. Сочетательное. Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель. a·(b·c)=(a·b)·c

3. Сумма n слагаемых, каждое из которых равно 1, равна n. a·1=а

4. Сумма n слагаемых, каждое из которых равно 0, равна 0. a·0=0

5. Распределительное свойство умножения относительно сложения. Для того чтобы умножить сумму на число, можно умножить на это число каждое из слагаемых и сложить получившиеся произведения. (a+b)·c=a·c+b·c

6. Распределительное свойство умножения относительно вычитания. Для того чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе. (a−b)·c=a·c−b·c

Свойства деления

1. При делении любого числа на 1, получается это же число.

2. При делении числа на это же число получается 1.

3. При делении нуля на число получается нуль.

Определения

Уравнение – это равенство, содержащее букву, значение которой нужно найти.

Корень уравнения – значение буквы, при котором из уравнения получается верное числовое равенство.

Решить уравнение – значит найти все его корни (или убедиться, что корней нет).

Умножить число m на натуральное число n – значит найти сумму n слагаемых, каждое из которых равно m.

Действия первой ступени – сложение и вычитание чисел.

Действия второй ступени – умножение и деление чисел.

Произведение чисел n и n называют квадратом числа n. Пишут n∙n=n²

Произведение n∙n∙n называют кубом числа n и обозначают n³.

Формула – запись правила с помощью букв.

Фигуры называют равными, если одну из них можно так наложить на другую, что эти фигуры совпадут. площади и периметры равных фигур так же равны.

Периметр фигуры – это сумма длин ее сторон.

Гектар – это площадь квадрата со стороной 100м.

Ар(сотка) – это площадь квадрата со стороной 10м.

Грани прямоугольного параллелепипеда – это прямоугольники, из которых состоит его поверхность.

Ребра прямоугольного параллелепипеда – это стороны его граней.

Вершины прямоугольного параллелепипеда – это вершины его граней.

Измерения прямоугольного параллелепипеда – это его длина, высота и ширина.

Куб – это прямоугольный параллелепипед, у которого все измерения равны.

Кубический сантиметр (мм, дм и т.д.) – это объем куба с ребром 1см (мм, дм и т.д.).

Литр – это кубический дециметр.

Окружность – замкнутая линия.

Круг – часть плоскости внутри окружности.

Центр окружности – точка, одинаково удаленная от всех точек, лежащих на окружности.

Радиус – отрезок, соединяющий центр окружности с любой из точек, лежащих на окружности.

Диаметр – отрезок, проходящий через центр окружности и соединяющий две точки, лежащие на окружности.

Правильная дробь – дробь, у которой числитель меньше знаменателя. правильная дробь меньше единицы.

Неправильная дробь – дробь, у которой числитель больше знаменателя. Правильная дробь больше или равна единице.

Алгоритмы

• Нахождение неизвестных: слагаемого, уменьшаемого, вычитаемого, множителя, делимого, делителя (из начальной школы).

• Чтобы найти делимое при делении с остатком, надо умножить неполное частное на делитель и прибавить к полученному произведению остаток.

• Чтобы найти площадь прямоугольника надо его длину умножить на ширину.

• Площадь всей фигуры равна сумме площадей ее частей.

• Чтобы найти объем прямоугольного параллелепипеда нужно его длину умножить на ширину и на высоту.

• Чтобы найти площадь поверхности прямоугольного параллелепипеда, необходимо сложить площади всех его граней.

• Из двух дробей с одинаковым знаменателем меньше та дробь, у которой числитель меньше, и больше та дробь, у которой числитель больше.

• При сложении дробей с одинаковыми знаменателями числители дробей складывают, а знаменатель остается тот же.

• При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тем же.

Памятка по основным темам. Математика 5 класс

Угол. Измерение угла — урок. Математика, 5 класс.

Геометрическая фигура угол образуется из двух лучей с общей начальной точкой.

Общая точка называется вершиной угла, а лучи — сторонами угла.

Если угол образован дополнительными (или противоположными) лучами, то он называется развёрнутым.

Для названия угла часто используют три большие латинские буквы, название вершины угла пишется посередине.

Иногда угол можно назвать только одной буквой, которая находится у вершины.

Можно также познакомиться с греческим алфавитом и использовать маленькие буквы для названий углов.

Чаще используют: α,β,γ,δ,ϵ,η,ϕ,ω — и другие.

Попытаемся представить точку как что-то бесконечно маленькое, а прямую — как что-то бесконечно простирающееся в обе стороны.

Пример:

описание рисункa:

1. на рисунке показан угол ∡ABC, ∡B или ∡α;

2. также нарисован развёрнутый угол ∡KLM.

Так же как каждый отрезок имеет длину, которую можно измерить линейкой и выразить в единицах измерения, так и каждый угол имеет величину.

За единицу измерения углов принимают градус, что является 1180 частью развёрнутого угла.

Величина развёрнутого угла — \(180°\).

Углы измеряют транспортиром.

Особый угол, половина развёрнутого угла — прямой угол.

Прямой угол обозначают маленьким квадратиком внутри угла.

Величина прямого угла равна \(90°\).

Углы, величина которых меньше \(90°\), называются острыми.

Углы, величина которых больше \(90°\), называются тупыми.

Прямоугольный параллелепипед — урок. Математика, 5 класс.

Вокруг нас мы часто встречаем предметы, имеющие форму коробки.

Они могут быть сделаны из разного материала и окрашены в разные цвета, но по форме они напоминают друг друга: коробки, шкафы, здания и т. п.

Все эти предметы напоминают геометрическое тело — прямоугольный параллелепипед.

Поверхность его состоит из \(6\) прямоугольников, которые называются гранями прямоугольного параллелепипеда.

Две грани называются противоположными, если у них нет общего ребра. Каждые две противолежащие грани равны.

Грани можно назвать в зависимости от того, как мы видим прямоугольный параллелепипед:

та грань, которая обращена к нам, называется передней;

точно такая же грань имеется сзади — это задняя грань;

боковые грани также являются равными прямоугольниками; 

та грань, которая находится сверху, называется верхней;

а грань, на которой фигура стоит, называется нижней, или основанием, и эти две грани равны.

Стороны граней называются рёбрами, а вершины граней — вершинами параллелепипеда.

У прямоугольного параллелепипеда всего \(6\) граней (передняя, задняя, нижняя, верхняя и две боковые), \(12\) рёбер и \(8\) вершин.

Рёбра, которые имеют общую вершину, называют измерениями прямоугольного параллелепипеда (на нижнем рисунке — красные рёбра).

Куб — это прямоугольный параллелепипед, у которого все измерения равны, то есть поверхность куба состоит из \(6\) равных квадратов.

Законы арифметических действий. Вычисления с многозначными числами. Математика, 5 класс: уроки, тесты, задания.

Первые уроки математики в 5 классе

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

Первые уроки математики в 5 классе

2 слайд

Описание слайда:

Математика – самая древняя из наук, она была и остается необходимой людям. Слово «математика» греческого происхождения. Оно обозначает «наука», «размышление». Математику уже затем учить надо, что она ум в порядок приводит. М.В. Ломоносов

3 слайд

Описание слайда:

Первый отечественный учебник по математике вышел в 1703 год. Леонтий Филиппович Магницкий издал «Арифметику». По ней учился М. В. Ломоносов, называвший этот учебник «вратами учёности». По этому учебнику мы будем изучать математику в 5 классе.

4 слайд

Описание слайда:

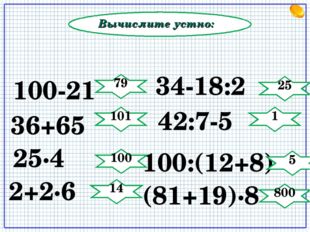
Вычислите устно: 34-18:2 (81+19)∙8 25∙4 42:7-5 100:(12+8) 2+2∙6 100-21 36+65 79 101 14 100 25 1 5 800

5 слайд

Описание слайда:

6 слайд

Описание слайда:

7 слайд

Описание слайда:

9999: 9 + ( 506 – 127 · 2 ) · 10 – 13 = 1620 + ( 46 — 4 · 8 ) · 10 – 362 = 1 2 3 4 5 6 1 2 3 4 5

8 слайд

Описание слайда:

9 слайд

Описание слайда:

№1. Кот Матроскин сшил скатерть прямоугольной формы, размеры которой 2 м и 3 м.Найдите периметр и площадь данной скатерти. №2. Кот Матроскин и Шарик катятся на санках со скоростью 16 м/мин. Как долго они будут катится с горы, если её длина 96 метров?

10 слайд

Описание слайда:

96:16=6(мин) – едут с горы Матроскин и Шарик (2+3)∙2=10(м) – периметр скатерти 2∙3=6(м²) – площадь скатерти

11 слайд

Описание слайда:

12 слайд

Описание слайда:

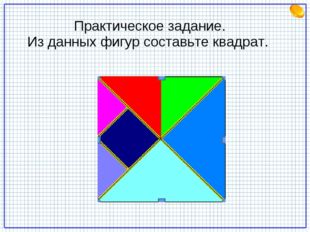
Практическое задание. Из данных фигур составьте квадрат.

13 слайд

Описание слайда:

14 слайд

Описание слайда:

15 слайд

Описание слайда:

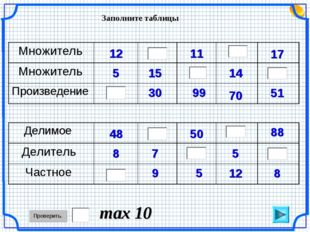
Заполните таблицы 12 15 5 30 11 70 14 99 48 7 8 9 50 12 5 5 17 51 88 8 max 10 Делимое Делитель Частное Множитель Множитель Произведение

16 слайд

Описание слайда:

17 слайд

Описание слайда:

Запишите числа: Четыреста восемнадцать Девятьсот сорок пять Одна тысяча сорок семь Пять тысяч триста семнадцать Восемь тысяч девять Триста тысяч двадцать семь Пятьдесят две тысячи одиннадцать Проверьте себя: 418, 945, 1047, 5318, 8009, 300027, 52 011

18 слайд

Описание слайда:

Вычислите: 52843+6391 59234 93619-4056 89563 5220:145 158130 315 ∙ 502 36

19 слайд

Описание слайда:

Решите уравнения: 12х=1212 х=513-361 х=152 х-315=802 х=802+315 х=1117 361+х=513 х=1212:12 х=101 434:х=7 х=434:7 х=62

20 слайд

Описание слайда:

Устно 1. Прочитайте число: 380, 907, 60 239, 102 400, 999 999 2. Сколько цифр используется для записи числа 640 046? 3. Назовите число: Следующее за числом 99 Предшествующее числу 300 Следующее за числом 19 999 Предшествующее числу 1 200 На 1 меньше числа 700 На 1 больше числа 8999

21 слайд

Описание слайда:

Решите уравнения х · 45 = 945 х : 16 = 31 74 · х = 4292 1440 : х = 6

22 слайд

Описание слайда:

Решите задачу: Расстояние от дома дяди Фёдора до Простоквашино равно 326 км. Папин Запорожец, проехав 5 часов со средней скоростью 65 км/ч, сломался. Сколько километров папа и дядя Фёдор «толкали» машину? 65∙5=325(км) – проехал Запорожец 326-325=1(км) – папа и дядя Фёдор толкали машину.

23 слайд

Описание слайда:

Решите задачу: 2) С какой скоростью ехал поезд обратно? Родители дяди Фёдора поехали отдыхать в Сочи на поезде, который ехал со скоростью 110 км/ч. Через 15 часов они приехали на место. На обратный путь же они потратили 10 часов. С какой скоростью ехал поезд обратно? 1) Каково расстояние от Москвы до Сочи? 110∙15=1650(км) 1650:10=165(км)

24 слайд

Описание слайда:

№1. Пильщики распиливают бревно на метровые обрубки. Длина бревна – 5 метров. Распиловка бревна поперек отнимает каждый раз полторы минуты. Сколько минут потребуется, чтобы распилить все бревно? №2. Четыре кошки и 3 котенка весят 15 килограммов, а 3 кошки и 4 котенка весят 13 килограммов. Предполагается, что все взрослые кошки весят одинаково и котята также весят одинаково. Сколько весит каждая кошка и каждый котенок в отдельности?

25 слайд

Описание слайда:

Курс профессиональной переподготовки

Учитель математики

Курс повышения квалификации

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс:
Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник:
Все учебники

Выберите тему:
Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала:

ДБ-175409

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий