Формулы для 6 класса по математике: Основные правила математики. 6 класс – Формулы по математике за 6 класс — Молитва

Содержание

Основные правила математики. 6 класс

Содержание

Делимость натуральных чисел

Если натуральное число делится нацело на натуральное число , то число называют кратным числа , число — делителем числа .

Для любого натурального числа каждое из чисел

$a \cdot 1,a \cdot 2,a \cdot 3, \ldots$

является кратным числа .

Наименьшим делителем любого натурального числа является число , а наибольшим — само число .

Среди чисел, кратных , наибольшего нет, а наименьшее есть — это само число .

Если каждое из чисел и делится нацело на число ,то и сумма a+k также делится нацело на число .

Если число делится нацело на число , а число не делится нацело на число , то сумма a+b также не делится нацело на число .

Простые и составные числа

Натуральное число называют простым, если оно имеет только два разных делителя: единицу и само это число.

Натуральное число, имеющее более двух делителей, называют составным.

Любое составное число можно представить в виде произведения простых чисел, то есть разложить на простые множители.

Если наибольший общий делитель двух натуральных чисел равен 1, то их называют взаимно простыми.

Признаки делимости натуральных чисел

Если запись натурального числа оканчивается цифрой 0, то это число делится нацело на 10.

Если запись натурального числа оканчивается любой цифрой, отличной от 0, то это число не делится нацело на 10.

Если натуральное число разделить на 10, то остаток равен числу, записанному последней цифрой этого числа.

Если запись натурального числа оканчивается четной цифрой, то это число делится нацело на 2.

Если запись натурального числа оканчивается нечетной цифрой, то это число не делится нацело на 2.

Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5.

Если запись натурального числа оканчивается любой цифрой, отличной от цифр 0 и 5, то это число не делится нацело на 5.

Если сумма цифр натурального числа делится нацело на 9, то и само число делится нацело на 9.

Если сумма цифр натурального числа не делится нацело на 9, то и само число не делится нацело на 9.

Если сумма цифр натурального числа делится нацело на 3, то и само число делится нацело на 3.

Если сумма цифр натурального числа не делится нацело на 3, то и само число не делится нацело на 3.

Основное свойство дроби

Если числитель и знаменатель данной дроби умножить на одно и то же натуральное число, то получим дробь, равную данной:

Если числитель и знаменатель данной дроби разделить на их общий делитель (или на одно и то же натуральное число), то получим дробь, равную данной:

Сокращение дробей

Деление числителя и знаменателя дроби на их общий делитель, отличный от 1, называют сокращением дроби.

Дробь, числитель и знаменатель которой — взаимно простые числа, называют несократимой.

Если сократить дробь на наибольший общий делитель числителя и знаменателя, то получим несократимую дробь.

Приведение дробей к наименьшему общему знаменателю

Чтобы привести дроби к наименьшему общему знаменателю, надо:

найти наименьший общий знаменатель данных дробей;
найти дополнительные множители для каждой из дробей, разделив общий знаменатель на знаменатели данных дробей;
умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Целые числа. Рациональные числа

Все натуральные числа, противоположные им числа и число 0 называют целыми числами.
Натуральные числа называют целыми положительными числами. Числа -1, -2, -3, … называют целыми отрицательными числами.
Объединив натуральные числа с целыми отрицательными и нулем, получим целые числа.
Объединив целые числа с дробными, получим рациональные числа.

Модуль числа

Модулем числа называют расстояние от начала отсчета до точки, изображающей это число на координатной прямой.
Модуль числа обозначают так: (читают: «модуль a»).
Модуль положительного числа равен этому числу; модуль отрицательного числа равен числу, противоположному данному;

Модуль числа принимает только неотрицательные значения. Модули противоположных чисел равны:

Сложение и вычитание дробей

Чтобы сложить две дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же.
Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Чтобы сложить (вычесть) две дроби с разными знаменателями, надо привести их к общему знаменателю, а потом применить правило сложения (вычитания) дробей с одинаковыми знаменателями.

Сложение и вычитание рациональных чисел

Чтобы сложить два числа с разными знаками, надо:

найти модули слагаемых;
из большего модуля вычесть меньший модуль;
перед полученным числом поставить знак слагаемого с большим модулем.

Чтобы сложить два отрицательных числа, надо:

найти модули слагаемых;
сложить модули слагаемых;
перед полученным числом поставить знак «-».

Сумма двух противоположных чисел равна нулю:

-a+a=0 или a-a=0
Для любого рационального числа :

Чтобы найти разность двух чисел можно

к уменьшаемому прибавить число, противоположное вычитаемому.

Умножение. Свойства умножения

Произведением числа на натуральное число не равное 1, называют сумму, состоящую из слагаемых, каждое из которых равно а:

Если один из двух множителей равен 1, то произведение равно второму множителю:

$m \cdot 1 = 1 \cdot m = m$

Если один из множителей равен нулю, то произведение равно нулю:

$m \cdot 0 = 0 \cdot m = 0$

Если произведение равно нулю, то хотя бы один из множителей равен нулю.

Умножение обыкновенных дробей

Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения:

Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Чтобы умножить смешанные числа, надо сначала записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Умножение рациональных чисел

Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак «-».

Чтобы умножить два отрицательных числа, надо умножить их модули.

Для любого рационального числа :

Если произведение $a \cdot b$ – положительное, то числа и имеют одинаковые знаки;

Если произведение $a \cdot b$ – отрицательное, то числа и имеют разные знаки.

Деление обыкновенных дробей

Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:

Деление рациональных чисел

Чтобы найти частное двух чисел с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «-».
Чтобы найти частное двух отрицательных чисел, надо модуль делимого разделить на модуль делителя.

Нахождение дроби от числа

Чтобы найти дробь от числа, можно число умножить на эту дробь.

Чтобы найти проценты от числа, можно представить проценты в виде дроби и умножить число на эту дробь.

Нахождение числа по его дроби

Чтобы найти число по значению его дроби, можно это значение разделить на эту дробь.

Чтобы найти число по его процентам, можно представить проценты в виде дроби и разделить значение процентов на эту дробь.

Степень числа

Степенью числа с натуральным показателем , большим 1, называют произведение множителей, каждый из которых равен :

Число при этом называют основанием степени.

Степенью числа с показателем 1 называют само число

Вторую степень числа называют также квадратом числа. Например, запись a^2 читают: « в квадрате». Третью степень называют кубом числа, а запись a^3 читают: « в кубе».

Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а затем производят другие действия.

Числовые и буквенные выражения

Запись, составленную из чисел, знаков арифметических действий и скобок, называют числовым выражением.

Запись, составленную из чисел, букв, знаков арифметических действий и скобок, называют буквенным выражением.

Раскрытие скобок

Если перед скобками стоит знак «-», то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, изменить на противоположные.

Если перед скобками стоит знак « + », то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, оставить без изменений.

Приведение подобных слагаемых

Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.

Свойства уравнений

Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.
Если данное уравнение не имеет корней, то, прибавив к обеим его частям одно и то же число, получим уравнение, тоже не имеющее корней.
Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.
Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.

Отношения

Пропорции

Равенство двух отношений называют пропорцией. В буквенном виде пропорцию можно записать так:

или

Числа и называют крайними членами пропорции, а числа и — средними членами пропорции.

Основное свойство пропорции

Произведение крайних членов пропорции равно произведению ее средних членов:

Если , , и числа, не равные нулю, и $a \cdot d = b \cdot c$ , то отношение и могут образовывать пропорцию

Процентное отношение двух чисел

Процентное отношение двух чисел — это их отношение, выраженное в процентах. Оно показывает, сколько процентов одно число составляет от другого.

Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.

Прямая пропорциональная зависимость

Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.

Если величины и прямо пропорциональны, то их соответствующие значения удовлетворяют равенству $y = \frac{k}{x}$ , где – число, постоянное для данных величин.

Данная информация взята из УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир

Формулы по математике за 6 класс

Автор Administrator На чтение 2 мин. Опубликовано 26.04.2016

Иногда учащимся 6 классов бывает достаточно сложно решать те или иные математические задачи или уравнения, не имея под рукой основных математических формул. Даже для взрослого человека трудно удержать в голове все необходимые формулы и значения, а для ребенка тем более. Для этого составлены, так называемые, пособия-памятки, которые содержат необходимую информацию по математике.

Книга представляет собой сборник практической информации, которая выручит учащихся при выполнении различных математических заданий. В нем можно найти:

таблицу законов сложения и умножения;
таблицу дробей и процентов;
основные математические и геометрические формулы;
таблицу единиц измерения

Для родителей это пособие также окажется полезным. Если они решат помочь своим детям в решении какой-либо задачи, то благодаря этому сборнику восстановят в памяти основные формулы по математике для 6 класса.

Имея под рукой все формулы по математике за 6 класс, ученикам будет легко ориентироваться в большом объеме математической информации. Это поможет облегчить работу не только в домашних условиях, но и на уроках в классе. Учителя не будут испытывать необходимость в повторении той или иной формулы на каждом уроке, что сэкономит гораздо больше времени.

Издательство: Все Для Детей
Год издания: 2014
Автор: Все Для Детей
Формат: PDF
Количество страниц: 11
Язык: Русский

Скачать бесплатно formuly-po-matematike-6-klass.pdf

Опорные конспекты по математике 6 класс

Выберите документ из архива для просмотра:

Выбранный для просмотра документ опорн консп деление дробей 6 кл.docx

Выбранный для просмотра документ опорн консп деление пол и отрчисел 6 кл.docx

Выбранный для просмотра документ опорн консп делители и кратные 6 кл.docx

Делители и кратные

Делителем b натурального числа а называют натуральное число b, на которое а делится без остатка.

Задание

Найти все делители числа 12.

Ещё одним важным понятием темы будет понятие «кратное».

Например

Все эти числа делятся на 7.

Пример

В пачке по 10 печений. Не раскрывая пачек, можно взять 10 печений, 20 печений, 30 печений.

А вот 23 печенья взять нельзя.

Говорят, числа кратные 10 это 10, 20, 30. Число 23 не кратно числу 10.

Если натуральное числа а делится на натуральное число b, то число а называют кратным числа b.

Другими словами, число а кратно числу b – значит а делится на b.

Теперь поговорим о количестве делителей и кратных.

Для числа 10 делителей будет 4: 1, 2, 5 и 10.

Теперь запишем кратные 10: 10, 20, 30, 100, 1000, …

Запомним, любое натуральное число имеет бесконечно много кратных и ограниченное число делителей.

Выбранный для просмотра документ опорн консп длина окр 6 кл.docx

Выбранный для просмотра документ опорн консп дробные выражения 6 кл.docx

Выбранный для просмотра документ опорн консп коорд плоскость 6 кл.docx

Выбранный для просмотра документ опорн консп координаты на прямой 6 кл.docx

Выбранный для просмотра документ опорн консп масштаб 6 кл.docx

Выбранный для просмотра документ опорн консп модуль числа 6кл.docx

Выбранный для просмотра документ опорн консп нахождение дроби от числа 6 кл.docx

Выбранный для просмотра документ опорн консп нахождение числа по дроби 6 кл.docx

Выбранный для просмотра документ опорн консп нод 6 кл.docx

Выбранный для просмотра документ опорн консп нок 6 кл.docx

Выбранный для просмотра документ опорн консп площадь круга 6 кл.docx

Выбранный для просмотра документ опорн консп приведение подобных 6 кл.docx

Выбранный для просмотра документ опорн консп признаки делимости на 10,5,2 класс 6.docx

Выбранный для просмотра документ опорн консп признаки делимости на 9 и 3 класс 6.docx

Выбранный для просмотра документ опорн консп пропорция 6 кл.docx

Пропорция

Определение. Пропорция – это равенство двух отношений.

где: a, b, c и d – называют членами пропорции.

a и d – это крайние члены пропорции,

b и c – средние члены пропорции.

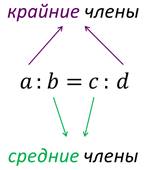
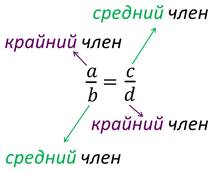
Например

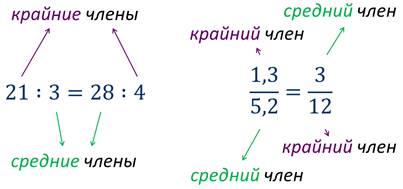
Основное свойством пропорции. В любой верной пропорции произведение крайних членов равно произведению средних членов пропорции, т.е.

Верно и обратное утверждение: если произведение крайних членов равно произведению средних членов a · d = b · c, то пропорция a : b = c : d верна. Оно называется признаком пропорции.

Если в верной пропорции поменять местами средние члены и крайние члены, то получившиеся новые пропорции также верны.

Например

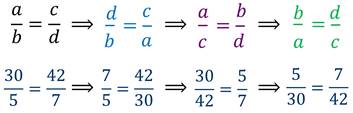
Если три члена пропорции известны, а четвёртый нужно найти, то говорят, что это задача на пропорцию. Задачи на пропорции возникают очень часто. Нужно только научиться уверенно их решать.

Задача

Мама дяди Фёдора из Простоквашино решила сварить для него яблочное варенье из 3 кг яблок. По рецепту на 2 кг яблок нужно 3 кг сахара. Сколько сахара понадобится маме дяди Фёдора для приготовления 3 кг варенья?

Решение:

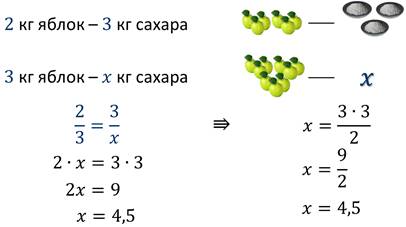
Сформулируем правило для нахождения неизвестного крайнего члена пропорции:

чтобы найти неизвестный крайний член пропорции, нужно произведение её средних членов разделить на известный крайний член пропорции.

Совершенно аналогично формируется правило для нахождения неизвестного среднего члена пропорции:

чтобы найти неизвестный средний член пропорции, нужно произведение её крайних членов разделить на известный средний член.

Задание

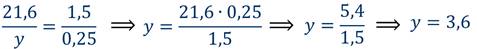
Выбранный для просмотра документ опорн консп разлож на прост множители 6 кл.docx

Выбранный для просмотра документ опорн консп распредел свойство 6кл.docx

Применение распределительного свойства умножения

Итак, распределительное свойство умножения относительно сложения гласит, что для того чтобы умножить сумму на число, можно умножить на это число

каждое слагаемое и сложить получившиеся произведения.

Распределительное свойство умножения относительно вычитания говорит, что

для того чтобы умножить разность на число, можно умножить на это число

уменьшаемое и вычитаемое и из первого произведения вычесть второе.

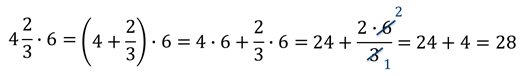
Мы применили распределительное свойство умножения относительно сложения и упростили себе вычисления.

Запишем правило:

Чтобы умножить смешанное число на натуральное число, можно:

1) умножить целую часть на натуральное число;

2) умножить дробную часть на это натуральное число;

3) сложить полученные произведения.

Пример

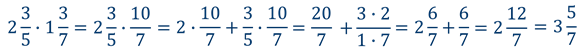
Правило умножения смешанных чисел:

Для того чтобы умножить смешанное число на смешанное число, можно:

1) перевести одно смешанное число в неправильную дробь;

2) умножить целую часть второго множителя на неправильную дробь;

3) умножить дробную часть второго множителя на неправильную дробь;

4) сложить полученные результаты.

Пример

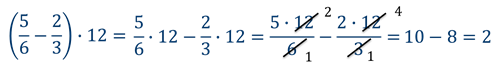
Задание

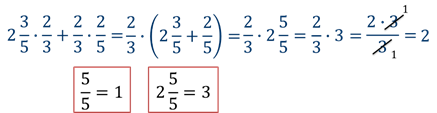
Используя распределительное свойство умножения можно упрощать и буквенные выражения.

Например

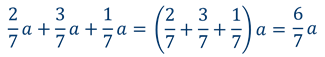
Выбранный для просмотра документ опорн консп решение уравнений 6 кл.docx

Решение уравнений

Уравнение – это равенство, содержащее переменную, значение которой надо найти.

Значение переменной, при котором из уравнения получается верное числовое равенство, называют корнем уравнения.

Решить уравнение – значит найти все его корни, или убедиться, что уравнение не имеет корней.

Вывод:

Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число.

Вывод:

Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.

И решим ещё одно уравнение:

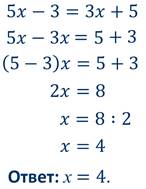
Чтобы решить уравнение, содержащее подобные слагаемые нужно:

1) слагаемые, содержащие переменную, перенести в левую часть уравнения, а числа – в его правую часть, не забывая при переносе менять знаки на противоположные;

2) привести подобные слагаемые в левой и правой частях уравнения;

3) разделить число в правой части на коэффициент при переменной.

Во всех рассмотренных нами примерах мы уравнения приводили к виду:

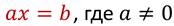
Определение

Уравнение, которое можно привести к такому виду с помощью переноса слагаемых и приведения подобных слагаемых, называют линейным уравнением с одним неизвестным.

Выбранный для просмотра документ опорн консп слож и выч смешан чисел 6 кл.docx

Выбранный для просмотра документ опорн консп слож отр чисел 6 кл.docx

Выбранный для просмотра документ опорн консп срав слож выч дробей с разн знам 6кл.docx

Выбранный для просмотра документ опорн консп сравнениечисел 6 кл.docx

Выбранный для просмотра документ опорн консп умн пол и отр чисел 6 кл.docx

Выбранный для просмотра документ опорн конспект вз обр числа 6 кл.docx

Взаимно обратные числа

Определение

Два числа, произведение которых равно единице, называют взаимно обратными.

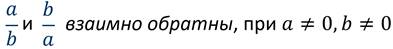
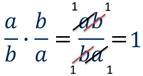
Если одно из двух взаимно обратных чисел – правильная дробь, то другое обязательно неправильная дробь.

Число 1 взаимно обратно самому себе, а число 0 не имеет обратного себе числа.

Значит, чтобы выяснить, являются ли два числа взаимно обратными, их надо перемножить.

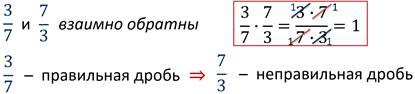
Если ответ равен единице, то числа – взаимно обратные.

Запомним несколько полезных правил:

Чтобы найти число взаимно обратное данному, надо:

1) Если число натуральное нужно представить его в виде дроби и перевернуть (поменять местами числитель и знаменатель).

2) Если число обыкновенная дробь нужно дробь перевернуть, а затем выделить целую часть.

3) Если число смешанное нужно представить его в виде неправильной дроби, затем перевернуть.

4) Если число десятичная дробь нужно представить его в виде дроби, затем перевернуть и выделить целую часть.

Конспект урока математики в 6 классе по теме «Составление формул»

Конспект урока математики в 6 классе

по теме : «Составление формул»

Тип урока: закрепление нового материала (2 урок из 3), интегрированный.

Цели :

Обучающая — продолжить формирование навыка у учащихся составлять формулы и работать с ними, применить полученные формулы в практической работе;

Развивающая – развивать умение выделять главное в изучаемом материале;
развивать самостоятельность учащихся; стимулировать интерес учащихся к математике;

Воспитывающая – воспитывать ответственное отношение к учебному труду; умение преодолевать учебные трудности; умение работать в коллективе, воспитывать дружеские отношения в классе методом групповой организации выполнения заданий.

Ход урока.

Организационный момент.

Здравствуйте ребята! Сегодня у нас урок-закрепление новой темы. Тема урока записана в лабиринте на доске. Попрошу вас прочитать ее.

Правильно. Составление формул на уроке математики. Именно, на уроке математики ,т.к. формулы встречаются и по другим предметам. Вы подготовили такие сообщения и чуть позже расскажете о формулах, которые встречаются на уроке физики, географии, химии, информатики, биологии. Сегодня мы продолжим учиться составлять формулы.

Открыли тетради и записали тему урока.

2)Проверка домашней работы. Устная проверка №1105 и №1106 (учебник под редакцией Г.В.Дорофеева, И.Ф.Шарыгина. 6 класс.)

3)Устный счет. А сейчас послушайте интересную информацию, чтобы потом отгадать слово.

Со времени первых славянских памятников и до начала XVIII века для обозначения чисел употреблялись буквы. Над буквами, применяемыми для обозначения чисел, ставились специальные знаки-титла. Чтобы отделить такие буквы-числа от текста, спереди и сзади ставились точки. Этот способ обозначения цифр был заимствован славянами из греческого языка. Поэтому цифры обозначались только теми буквами, для которых есть соответствия в греческом алфавите.

Очень любопытны названия больших чисел. Вот как они именуются в прописи, написанной в 1643году: “Десять тысяч – тьма, десять тем – легион, десять легионов – леор, десять леоров – ворон, десять воронов – колода.”

Конечно, неудобство такого способа обозначения чисел очевидна. Поэтому Петр I и ввел в России, привычные нам, десять цифр. Если вы верно вычислите примеры и выберете правильные ответы, то узнаете, как назывался способ обозначения цифр с помощью букв.

(Писать в тетради только ответ и букву, стоящую рядом с ним, чтобы потом прочитать слово. Поставлю оценку тому, кто первый скажет слово.)

1) –1/5 ^__ 1/10

Г.3/10 К.1/10 Ч.—1/10 Ц.—3/10

2) 1,5 (^__1+3)

А.1,5 И.3 У.6 Е.—3

3) 2 : 1/4

К.1/8 Н.1/2 Ф.8 Ш.2

4) 0,2 (—8)

А.1,6 И.—1,6 Р.16 Т.—0,16

5) 1—3/5

Р.2/5 С.3/5 Т.8/5 Ч.—2/5

6) (— 1/4)²

^{А.2/8 И.—1/16 У. 1/8 Ь. 1/16}

ОТВЕТ: ЦИФИРЬ.

4)Повторение нового материала.

Давайте повторим формулы, которые изучили на предыдущем уроке.(Показываю карточки с формулами и прошу назвать эту формулу.)

P=a+b+c

P=2(a+b)=2a+2b

V=a b c

S=a b

Сформулируйте алгоритм составления формул.

Алгоритм:

Чтобы составить формулу, нужно:

обозначить буквами все величины, которые будут в нее входить;
выявить зависимость между этими величинами, записав ее в виде математического выражения;
приравнять полученное выражение к той величине, для которой составляется формула.

А теперь вернемся к тому, чтобы поговорить о формулах по другим предметам. Для этого вызываю к доске тех ребят, которые подготовили сообщения.

Формулы по физике.

F=mg — формула силы тяжести, где m – масса тела,

g – ускорение свободного падения.

I=U/R –закон Ома для участка цепи, где R – сопротивление,

U – разность потенциалов(напряжение).

F=m_*a – второй закон Ньютона, где a – ускорение тела,

m – масса тела,

F – сила.

Формулы по географии.

Р=З:Д – формула ресурсообеспеченности страны (района), где З – запасы страны, Д – добыча за год.

АП=4Н₁-4Н₀ – формула абсолютного прироста населения,

где 4Н₁— численность населения за данный год, 4Н₀– численность населения за предыдущий год.

Формулы по химии.

M=m/V – формула молярной массы, где m – масса вещества,

V – количество вещества.

А=Z+N – формула массового числа атома, где Z – число протонов,

N – число нейтронов.

4P+5O₂=2P₂O₅– реакция соединения.

Формулы по информатике.

I=log₂N—формула количества информации, если события равновероятны, где N – количество возможных событий.

A=m_*qⁿ—формула записи числа в формате с плавающей запятой,

где m – мантисса числа,

q –основание систем счисления,

n – порядок числа.

Формулы по биологии.

_{энергия света}

6CO₂+6H₂O —- C₆H₁₂O₆+6O₂! – уравнение фотосинтеза, где

СО₂ – углекислый газ,

H₂О – вода,

О₂ – кислород.

C₆H₁₂O₆ + 6O₂ —— CO₂+ 6H₂O + энергия ! –уравнение процесса дыхания, где СО₂ – углекислый газ,

H₂О – вода,

О₂ – кислород.

5)Закрепление нового материала. Показываю ребятам фигуры и прошу записать формулу периметра для этой фигуры. (Тетрадь двух учеников проверяю тут же.)

Далее решаем № 1107.Одного ученика вызываю к доске.

6)Самостоятельная работа. Сейчас небольшая самостоятельная работа, но прежде вспомним о математическом выражении, математическом предложении, математической формуле. Приведите свои примеры.

(Предлагаются карточки, где надо дописать слова : выражение, предложение, формула. Работа проводится по 4 вариантам в парах. )

1 вариант 2 вариант

а) k+6 — это … а) 7+d — это …

б) 4-3=1 — это … б) а=в+3 – это …

в) p=3ав — это … в) 7 а-чет.число – это …

г) 4-x <5 — это … г) k=4 а в – это …

д) V=а в с — это … д) с 10 – это …

3 вариант 4 вариант

а) P=2(а+в) — это … а) S=v t — это …

б) d-8 — это … б) D=8 а в – это …

в) W=7 c h — это … в) 7+3=10– это …

г) 5+y >10 — это … г) 7 с – это …

д) 4+5=9 — это … д) 10 < 12 – это …

7)Физкультминутка. Каждому ученику раздаю одну карточку с формулой и начинаю опрос. У кого формула периметра треугольника, поднимите карточку вверх, а затем сделайте приседание 3 раза. Теперь все вместе приседаем. У кого формула объема параллелепипеда, поднимите карточку вверх, а затем сделайте наклоны вперед 3 раза. Теперь все вместе делаем.

8)Закрепление нового материала. Выполняем №1109(а).Я на доске показываю как оформлять задачу. Решение №1109(б), № 1110, №1111.Вызываю ребят к доске.

9) Итог урока. Что сегодня делали на уроке? Что такое формула? Сформулируйте алгоритм составления формул.

Ребята, вы поработали хорошо. Я поставила оценки и ,в заключении, отгадайте такую загадку.

Ее «гранит» грызет студент

И школьник тоже спору нет,

И жизнь ей ученый посвятил

Сейчас о чем я говорил. (НАУКА.)

В любой науке встречаются формулы. Мы с вами только начали изучать формулы, как они составляются, и еще не один урок посвятим этому.

10) Домашнее задание. №1108, №1113.

Конспект урока математики для 6 класса по теме «Формула длины окружности. Урок -практикум»

Конспект урока математики.

Учитель: Балунова Инна Григорьевна.

ОУ: ГБОУ школа №5 Центрального района Санкт-Петербурга.

Класс: 6.

Тема: «Формула длины окружности. Урок практикум»

Цели урока: изучить формулу длины окружности и показать ее применение при решении задач.

Задачи:

Образовательные:

составление формулы, выражающей зависимость между величинами (вывод формулы длины окружности) ;
вычисление по формулам;
совершенствование вычислительных навыков;
обучение решению задач практического содержания
знакомство с историей возникновения новых понятий;
приобретение навыков исследовательской работы.

Воспитательные:

воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии;
воспитание ответственности, самостоятельности, умения работать в коллективе;
показать математику как интересную науку, превратить занятие в необычный урок, где может проявить себя каждый ученик.

Коррекционно-развивающие:

развитие и коррекция представлений об окружающем мире;
расширение и обогащение словаря учащихся через ведение новых слов и понятий;
формирование целенаправленных видов деятельности;
развитие приёмов умственной деятельности, памяти, внимания, умения сопоставлять, анализировать, делать выводы;
повышение информационной культуры учащихся, интереса к предмету;
формирование опыта работы в малых группах;
развитие познавательной активности, положительной мотивации к предмету.

Тип урока: интегрированный.

Формы обучения: индивидуальная, групповая.

Методы обучения: словесные, практические, наглядные.

Оборудование: компьютер, мультимедиа проектор, инструменты для измерения и построения (линейка, угольник, карандаш, ластик), карточки с заданиями, наборы для детского конструирования «Конструктор», верёвка.

ЦОР: презентация «Формула длины окружности. Урок-практикум»

Ход урока.

I. Организационный момент.

А знаете ли вы, что наша планета Земля имеет всего один спутник, который именуется Луна, что диаметр Земли почти в 13 раз больше диаметра ее спутника – Луны?! А знаете ли вы, какие научные орбитальные станции были запущены в космос для его освоения?!

Ответить сегодня на эти вопросы мы можем вместе.

Сегодня у нас урок – практикум по теме «Длина окружности» (слайд №1). Мы посвятим его освоению человеком космоса. Назовем урок «космическим», так как задачи, которые мы будем решать, тем или иным образом связаны с темой освоения космоса. Это будут задачи практического содержания, при решении их используются ваши знания по изученной теме (слайд №2).

II. Устный счёт.

Заполни «солнышко» (слайд №2)

III. Объяснение нового материала.

Актуализация ранее изученного материала.

Повторение теоретического материала по теме «Окружность».

Слайд №3. Задание учащимся. Найдите соответствие между понятием и определением.

Ответы:

Окружность – множество точек плоскости равноудалённых от некоторой точки.

Радиус окружности – отрезок, соединяющий точку окружности с её центром.

Диаметр окружности – отрезок, соединяющий две точки окружности и проходящий через её центр.

Круг – часть плоскости, ограниченная окружностью.

Приближённая формула для вычисления длины окружности.

Учащиеся выполняют работу в парах по плану. Для измерений используются деревянные цилиндры из набора для детского конструирования «Конструктор». Цилиндры имеют разный диаметр.

Учитель. Если опоясать цилиндр ниткой, а затем измерить её длину, то она приближённо будет равна длине окружности банки. Перед вами стоит задача – выполнить необходимые измерения и сделать выводы. Работу проделываем по плану.

Практическая работа в парах (слайд №4)

План работы.

1. Обернуть цилиндр ниткой.

2. Измерить длину нитки.

3. Измерить диаметр цилиндра.

4. Найти отношение длины окружности С к длине диаметра d, округлив число до сотых.

5. После измерений внести полученные данные в таблицу.

После выполнения измерений представитель от каждой пары выходит к доске и заносит полученные данные в таблицу (учитель вставляет данные прямо в таблицу презентации) (слайд №5)

Когда таблица будет заполнена, учащимся предлагается сделать вывод об отношении длины окружности к её диаметру (слайд №4).

Число π.

Сообщение о числе ПИ проводится с использованием слайдов №6 — №16

Слайд №6. Великий древнегреческий ученый Архимед, выполнив множество измерений установил, что длина окружности примерно в три целых одну седьмую раза больше диаметра окружности.

В трактате «Измерение круга» Архимед предлагает метод определения числа π , который использовался до конца 17 в., и указывает две удивительно точные границы числа π : 310/71< π < 31/7. Число π называют Архимедово число

Слайд №7. Обозначение π происходит от первой буквы греческого слова περιφέρεια «окружность». Впервые обозначение π появилось у английского математика Уильяма Джонса (1706г)

Слайд №8. Немного истории.

Изучением числа π занимались многие математики всех времен и народов, т.к. это число играет важную роль в математике, физике, астрономии, технике и т.д. Можно даже утверждать, что по характеру и полноте знаний о числе π возможно судить о научно техническом уровне развития данного общества.

Слайд. 9. Из древнеегипетских и вавилонских источников известно, что потребности того времени вполне удовлетворяло число, равное трем. Позже римляне принимали π равное 3,12.

В Древнем Египте π считали равным 256/81=3,1604…

В истории математики известно, что первое вычисление на основе строгих теоретических рассуждений было выполнено выдающимся математиком древности Архимедом.

Дальнейшая история числа связана с его вычислением.

Китаец Цзу Чунчжи в 5 веке нашел восемь правильных знаков.

В 15 веке иранский математик ал-Каши нашёл значение «ПИ» с 16 верными знаками

Слайд №10. Французский математик Франсуа Виет вычислил в 1579 году «ПИ » с 9 знаками.

Голландский математик Лудольф Ван Цейлен в 1596 году публикует результат своего десятилетнего труда – число ПИ, вычисленное с 35 знаками.

Леонард Эйлер в 1736 году опубликовал работу, в которой было вычислено 153 цифры числа «ПИ»

Слайд №11. Постепенно увеличивая точность значений…

При помощи суперкомпьютера число ПИ в наши дни вычислили с точностью до 2 триллионов 699 миллионов 990 тысяч знаков, а мы знаем всего первые три…

Слайд №12. 14 марта в мире отмечается один из самых необычных праздников — Международный день числа «Пи». Впервые День был отмечен в 1988 году в научно-популярном музее Эксплораториум в Сан-Франциско.

Слайд 13. Памятники числу ПИ.

Учитель предлагает учащимся несколько различных способов запоминая величины числа ПИ.

Способ 1. Слайд №14.

«ЧТО Я ЗНАЮ О КРУГЕ» (количество букв в каждом слове указывает на цифру в составе числа ПИ)

Способ 2. Слайд№15.

Чтобы нам не ошибаться,

Надо правильно прочесть:

Три, четырнадцать, пятнадцать,

Девяносто два и шесть.

Ну и дальше надо знать,

Если мы вас спросим —

Это будет пять, три, пять,

Восемь, девять, восемь.

Способ 3. Слайд №16. В учебнике Магницкого для закрепления в памяти этого выражения приведена рифмованная шутка:

Двадцать две совы скучали

На больших сухих суках.

Двадцать две совы мечтали

О семи больших мышах,

О мышах довольно юрких,

В аккуратных серых шкурках.

Слюнки капали с усов

У огромных серых сов

Вывод формулы длины окружности.

Слайд №17. Формулы длины окружности. C = 2 π r C = π d

Слайд №18. Физкультминутка.

IV. Формирование умений и навыков.

Решение задач на вычисление длины окружности.

Слайд №19.

Задача 1. Диаметр Солнца равен 1392000км. Найдите длину солнечного экватора (с точностью до тысяч километров).

Решение:

С=πd; С=3,14×1392000≈4370880≈4371000 км

Ответ: 4371000 км.

Слайд №20.

Задача 2. Диаметр Луны приблизительно равен 3476км. Найдите длину лунного экватора (с точностью до сотен километров).

Решение:

С=πd; С=3,14×3476≈10914,64≈10900 км

Ответ: 10900 км.

Слайд №21.

Задача 3. Длина земного экватора приблизительно 40 тыс.км. Найдите диаметр и радиус земного экватора (с точностью до сотен километров).

Решение:

С=πd, отсюда d=C/π=40000/3,14≈12738,85≈12700км.

Значит r=d/2≈12700/2≈6350км.

Ответ: 12700км и 6350км.

Справка (учитель): Луна – это спутник Земли, ее ближайший сосед в космосе. Она представляет собой каменистый шар размером с четверть Земли и является самым большим небесным телом в нашем ночном небе. Солнце – центр нашей Солнечной системы, огромный массивный шар, представляющий собой сгусток раскаленного газа. Солнце – мощный источник излучения света и теплоты. Земля – это единственная известная нам обитаемая планета. Земной шар имеет послойное строение. Внешний слой – оболочку – представляет земная кора.

Решение задач на вычисление диаметра и радиуса окружности.

Слайд №22.

Задача 4. Длина орбиты автоматической станции «Салют – 2» равна 41500км. Считая орбиту станции круговой, вычислите радиус орбиты.

Решение. Если считать орбиту круговой, то ее длину можно вычислить по формуле С=2πrорбиты, откуда rорбиты=С/2π=41500/6,28≈6608км.

Ответ: 6608км.

Справка (учитель после решенной и продемонстрированной задачи): Третья орбитальная космическая станция (ОКС) «Салют – 2» массой 18,5т была выведена на орбиту ракетой – носителем «Протон – К» 4 апреля 1973 года с космодрома Байконур. Перигей (минимальное удаление от Земли) орбиты составлял 216км, апогей (максимальное удаление от Земли) – 248км, наклонение – 51,6°. На 13-е сутки произошла разгерметизация отсеков ОКС, а 25 апреля перестала поступать телеметрическая информация. Станция, пробыв на орбите 54 дня, закончила свою работу и 28 мая 1973 года в результате естественного торможения в верхних слоях атмосферы упала в океан около Австралии. 28 мая сообщили, что «программа полета завершена» (не сказав «успешно»). Анализ причин аварии позволил предположить нештатную работу двигательной установки, что привело к прогоранию корпуса станции.

Тестовая работа на закрепление изученного материала.

Если интернет в классе работает бесперебойно, тестирование можно проводить в режиме онлайн. Тест выводится на экран, учащиеся отвечают на вопросы в тетради (слайд №23)

Если есть опасения, что будут технические неполадки, можно предложить модифицированный вариант теста (слайды №24 – №27).

V. Итоги урока.

Вопросы учащимся:

Чему примерно равно отношение длины окружности к её радиусу?
Назовите точную формулу длины окружности
Является ли π рациональным числом?
Каким рациональным числом может быть приближённо выражено число π ?
Назовите, чему равно число π с точностью до сотых, до десятитысячных.
Как найти радиус окружности, если известна её длина?

Выставление отметок.

Домашнее задание. Выучить формулы для вычисления длины окружности, диаметра и радиуса окружности. Стр. 256 № 1134, № 1135, стр.257 №1141.

Презентация по математике 6 класс по теме » Составление формул»

Инфоурок
›

Математика
›Презентации›Презентация по математике 6 класс по теме » Составление формул»

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

Составление формул –математика 6 класс. Учитель математики : Ткачук Наталья Петровна.

2 слайд

Описание слайда:

Актуализация знаний Х+15=31 а+в =31 2m=11 В:2=1,5 В-с>3 5· х<у

3 слайд

Описание слайда:

4 слайд

Описание слайда:

Пусть стороны треугольника обозначены буквами :а ,в, с. Составь буквенное выражение для подсчета периметра треугольника. ( Р) а в с Р=а +в +с Кто знает как можно назвать на математическом языке это буквенное выражение?

5 слайд

Описание слайда:

Постановка темы и цели урока. Какой математический термин вы услышали сегодня при составлении буквенного выражения для вычисления периметра треугольника? Какая тема нашего урока? Какие цели?

6 слайд

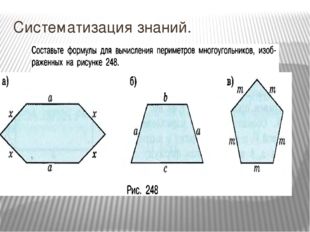
Описание слайда:

Систематизация знаний.

7 слайд

Описание слайда:

Систематизация знаний

8 слайд

Описание слайда:

Итоги урока. -Сегодня на уроке я узнал… -сегодня на уроке я научился… -Мне было трудно…

Курс профессиональной переподготовки

Учитель математики

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс:
Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник:
Все учебники

Выберите тему:
Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала:

ДБ-195724

Рабочая программа по математике для 6 класса

Математика.

Натуральные числа. Дроби. Рациональные числа

• понимать особенности десятичной системы счисления;

• оперировать понятиями, связанными с делимостью натуральных чисел;

• выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;

• сравнивать и упорядочивать рациональные числа;

• выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применение калькулятора;

• использовать понятия и умения, связанные с пропорциональностью величин, процентами, в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчёты.

• познакомиться с позиционными системами счисления с основаниями, отличными от 10;

• углубить и развить представления о натуральных числах и свойствах делимости;

• научиться использовать приёмы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.

• использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин.

• понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными.

• решать основные виды рациональных уравнений с одной переменной

• понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;

• овладеть специальными приёмами решения уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;

• вычислять длину окружности, площадь круга,

3. Содержание учебного предмета

Сложение и вычитание дробей с разными знаменателями

Сложение и вычитание положительных и отрицательных чисел

Умножение и деление положительных и отрицательных чисел

Итоговое повторение курса математики 6 класса

5. Календарно-тематическое планирование

урока

п/п

Тема урока

Повторение изученного материала в 5 классе(5 часов)

Повторение темы «Дроби. Арифметические действия с дробями»

Повторение темы «Решение уравнений»

Повторение темы «Проценты»

Диагностическая работа

Анализ контрольной работы

Делимость чисел (20ч)

Делители и кратные

Признаки делимости на 10, на 5 и на 2.

Признаки делимости на 9 и на 3

Простые и составные числа

Разложение на простые множители

Наибольший общий делитель. Взаимно простые числа

Наименьшее общее кратное

Контрольная работа №1 «НОД и НОК чисел»

Анализ контрольной работы

Сложение и вычитание дробей с разными знаменателями (22ч)

Основное свойство дроби

Сокращение дробей

Приведение дробей к общему знаменателю

Сравнение дробей с разными знаменателями

Сложение и вычитание дробей с разными знаменателями

Контрольная работа №2 «Сокращение, сложение и вычитание обыкновенных дробей»

Анализ контрольной работы

Сложение и вычитание смешанных чисел

Контрольная работа №3 «Сложение и вычитание смешанных чисел»

Анализ контрольной работы

Умножение и деление обыкновенных дробей (32ч)

Умножение дробей

Нахождение дроби от числа

Применение распределительного свойства умножения

Контрольная работа №4 «Умножение обыкновенных дробей»

Анализ контрольной работы

Взаимно обратные числа

Деление

Контрольная работа №5 «Деление дробей»

Анализ контрольной работы

Нахождение числа по его дроби

Дробные выражения

Контрольная работа №6 «Дробные выражения»

Анализ контрольной работы

Отношения и пропорции (20ч)

Отношения

Пропорции

Прямая и обратная пропорциональность

Контрольная работа №7»Отношения и пропорции»

Анализ контрольной работы

Масштаб

Длина окружности и площадь круга

Шар

Контрольная работа №8 «Окружность и круг»

Анализ контрольной работы

Рациональные числа. Положительные и отрицательные числа (12ч)

Координаты на прямой

Противоположные числа

Модуль числа

Сравнение чисел

Изменение величин

Контрольная работа №9 «Противоположные числа»

Анализ контрольной работы

Сложение и вычитание положительных и отрицательных чисел (12ч)

Сложение чисел с помощью координатной прямой

Сложение отрицательных чисел

Сложение чисел с разными знаками

Вычитание

Контрольная работа №10 «Сложение и вычитание положительных и отрицательных чисел»

Анализ контрольной работы

Умножение и деление положительных и отрицательных чисел (13ч)

Умножение

Деление

Рациональные числа

Свойства действий с рациональными числами

Контрольная работа №11 «Умножение и деление рациональных чисел»

Анализ контрольной работы

Решение уравнений (15ч)

Раскрытие скобок

Коэффициент

Подобные слагаемые

Контрольная работа №12 «Раскрытие скобок»

Анализ контрольной работы

Решение уравнений

Контрольная работа №13 «Решение уравнений»

Анализ контрольной работы

Координатная плоскость (12ч)

Перпендикулярные прямые

Параллельные прямые

Координатная плоскость

Столбчатые диаграммы

Графики

Контрольная работа №14 «Координатная плоскость»

Анализ контрольной работы

Итоговое повторение (11ч)

Признаки делимости. НОД и НОК

Арифметические действия с обыкновенными дробями

Отношения и пропорции

Сравнение, сложение и вычитание рациональных чисел

Умножение и деление рациональных чисел

Решение уравнений

Решение задач с помощью уравнения

Координатная плоскость

Итоговая контрольная работа

Анализ контрольной работы

Обобщающий урок

Формулы для 6 класса по математике: Основные правила математики. 6 класс – Формулы по математике за 6 класс

Основные правила математики. 6 класс

Основные правила математики. 6 класс

Содержание

Делимость натуральных чисел

Простые и составные числа

Признаки делимости натуральных чисел

Основное свойство дроби

Сокращение дробей

Приведение дробей к наименьшему общему знаменателю

Целые числа. Рациональные числа

Модуль числа

Сложение и вычитание дробей

Сложение и вычитание рациональных чисел

Чтобы сложить два числа с разными знаками, надо:

Чтобы сложить два отрицательных числа, надо:

Чтобы найти разность двух чисел можно

Умножение. Свойства умножения

Умножение обыкновенных дробей

Умножение рациональных чисел

Деление обыкновенных дробей

Деление рациональных чисел

Нахождение дроби от числа

Нахождение числа по его дроби

Степень числа

Числовые и буквенные выражения

Раскрытие скобок

Приведение подобных слагаемых

Свойства уравнений

Отношения

Пропорции

Основное свойство пропорции

Процентное отношение двух чисел

Прямая пропорциональная зависимость

Данная информация взята из УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир

Формулы по математике за 6 класс

Опорные конспекты по математике 6 класс

Конспект урока математики в 6 классе по теме «Составление формул»

Конспект урока математики для 6 класса по теме «Формула длины окружности. Урок -практикум»

Презентация по математике 6 класс по теме » Составление формул»

Рабочая программа по математике для 6 класса

Добавить комментарий Отменить ответ

Рубрики