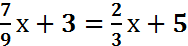Легкие уравнения 6 класс: Решение уравнений — урок. Математика, 6 класс. – Решение линейных уравнений. 6-й класс

как решать уравнения 6 класс

При решении уравнений необходимо помнить и в при необходимости использовать следующие правила:

1. Можно умножить или разделить обе части уравнения на одно и то же число, которое не равно нулю, при этом корни данного уравнения останутся неизменными.

Например:

Найдем корни данного уравнения:

Попробуем умножить левую и правую часть уравнения на число 9:

Теперь найдем корни полученного уравнения:

1. При решении уравнения его слагаемые можно перенести из одной части уравнения в другую, при этом изменяя их знак на противоположный. В таком случае корни уравнения не меняются.

Например:
Рассмотрим уравнение .
Чтобы его решить, перенесем число —13 в правую часть уравнения, изменяя его знак на противоположный (на +):

Проверим правильность найденного корня, подставив его значение в исходное уравнение:

Корень найден правильно.

1. Если в уравнении есть подобные слагаемые, то нужно все слагаемые с переменной перенести в одну часть уравнения (обычно в левую), а постоянные — в другую часть уравнения (в правую).}

Например:

Решение уравнений 6класс

Решение уравнений

Урок систематизации знаний учащихся 6класс

Вопросы на повторение.

1 Как называется равенство , содержащее букву?

2 Как называется значение неизвестного, при котором уравнение обращается в верное равенство?

3 Что значит решить уравнение?

Выполним устные упражнения:

1. Решите уравнение х+8=14 с помощью правила нахождения неизвестного слагаемого

2.Решите уравнение 7+х=15. 3. Решите уравнение 10х=80 с помощью правила нахождения неизвестного множителя?

4. Решите уравнение У:8=12.

5.Решить задачу с помощью уравнения. В классе 28 человек. 12 девочек . Сколько мальчиков в классе ?

Повторим свойства уравнений

1.Если к обоим частям данного уравнения прибавить (или вычесть)одно и тоже число , то получим уравнение , имеющее те же корни, что и данное. 2.Если какое-нибудь слагаемое перенести из одной части уравнения в другую , изменив при этом знак на противоположный , то получим уравнение , имеющее те же корни, что и данное. 3.Если обе части уравнения умножить( или разделить)на одно и тоже число , отличное от нуля число , то получим уравнение , имеющее те же корни, что и данное

1.Если к обоим частям данного уравнения прибавить (или вычесть)одно и тоже число , то получим уравнение , имеющее те же корни, что и данное.

Решим уравнение х+2=5. К обеим его частям прибавим число -2.Получим: х+2-2=5+(-2). Отсюда х=5-2 х=3 Ответ:3 Решите самостоятельно 11х=36-х, 32-5х=24 3х=28-х

2.Если какое-нибудь слагаемое перенести из одной части уравнения в другую , изменив при этом знак на противоположный , то получим уравнение , имеющее те же корни, что и данное.

Решим уравнение 3х+1=29-х Решение 3х+х=29-1 4х=28 х=28:4 х=7 Ответ:7

Решите самостоятельно

1) 5х+12=8х+30 2)4+9х=-2х+48 3)6х-17=-10-х

4)0,7-0,2х=0,3х-1,8 5)0,1х+9=0,2 х-4

Проверим ответы

1)-6 2) 4 3)1 4)5 5)130

Решим уравнение

2х-4=2х+6 2х-2х=6+4 0х=10 Ответ: решений нет

Решите уравнение

2х-10=2х-10 2х-2х=10-10 0х=0 Ответ : х-любое число

3.Если обе части уравнения умножить( или разделить)на одно и тоже число , отличное от нуля число , то получим уравнение , имеющее те же корни, что и данное

1)Решим уравнение 12х=48

2)Решим уравнение 4(х+5)=-28 Решение: х+5=-7 х=-7-5 х =-12 Ответ:-12 3)Решим уравнение 0,5у=0,24 Решение: 0,5ух2=0,24х2 х=0,48 Ответ:0,48

Решите самостоятельно

1)0,8(4х+4)=-3,2 2)-2,4(-7-9у)=-48 3)2,5х=62,5

Ответы1)-2, 2)- 3 ,3)25

Презентация по теме «Решение уравнений» в 6 классе презентацию подготовила учитель математики Мельник Наталья Николаевна МБОУ ЛИЦЕЙ №27им.И.Д.Смолькина город Новокузнецк 2018

Решение уравнений 6класс — Математика

Открытый урок

по математике по теме: «Решение уравнений»

6класс

Провела: Паль О.В.

2016 год

Открытый урок по математике в 6 классе

Тема урока: «Решение уравнений»(слайд1)

Цели:

Образовательные:

• закрепить знания, умения, навыки решения уравнений;

• закрепить понятие корня уравнения, правило переноса слагаемого из одной части уравнения в другую, правила умножения или деления обеих частей уравнения на одно и то же число, отличное от нуля.

Развивающие:

• развитие интеллектуальных умений: анализа алгоритма решения уравнения, условия задачи, логического мышления при построении алгоритма решения уравнения, вариативности выбора способа решения, систематизации уравнений по способам решения;

• развитие качеств личности – трудолюбия, аккуратности, настойчивости в достижении дел;

• развитие гибкости мышления, памяти, внимания и сообразительности;

• развитие математической речи;

• развитие зрительной памяти.

Воспитательные:

• воспитание познавательной активности;

• формирование навыков самоконтроля и самооценки;

• привитие математической грамотности;

• воспитание чувства товарищества, вежливости, дисциплинированности, ответственности, умения осуществлять совместную деятельность;

• формирование честности, ответственности.

Задачи урока:

1. Научить переносить знания от одного предмета к другому.

2. Снять монотонность урока и перегрузку учащихся, повысить интерес к математике, используя для этого различные методы проведения урока на разных его этапах.

3. Закрепить навыки действий с рациональными числами.

4. Закрепить навыки раскрытия скобок.

5. Закрепить навыки приведения подобных слагаемых

6.Закрепить навыки решения уравнений.

Тип урока: комбинированный

Оборудование: доска; мультимедийный проектор; презентация к уроку для демонстрации через проектор «Решение уравнений. pps»

Ход урока:

I.Организационный момент.

Здравствуйте ребята и уважаемые гости!

Прозвенел уже звонок

Начинается урок

Мы сегодня не одни

Гости на урок пришли!

2.Сообщение темы и целей урока (слайд 2)

—

Альберт Эйнштейн

Альберт Эйнштейн, один из основателей современной физики, сказал: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения (предлагается ученикам продолжить мысль учёного)
будут существовать вечно».

Вот сегодня мы и будем с вами заниматься вечным – решать уравнения. На предыдущих уроках вы решали уравнения и сегодня мы продолжаем отрабатывать умение решать уравнения, повторяем теоретический материал по теме «Решение уравнений» тем самым готовимся к контрольной работе.

III. Устная работа. «Разминка».

Теоретическое повторение: за правильный ответ дается жетон.

1. Что называется уравнением?

2. Что называется корнем уравнения?

3. Что значит « решить уравнение»?

4. Сколько корней может иметь уравнение?

Алгоритм решения уравнений:

Ребята, разминка закончилась, давайте подведем итоги устной работы. Учащиеся подсчитывают полученные жетоны. Оценивание своей работы.

IV. Закрепление

У каждого ученика листочек для внесения ответов.

1.Упростить выражение из правой таблицы
и поставить ему в соответствие выражение из левой таблицы

2.Найти уравнение, равносильное уравнению
2x — 6 = 5 – 7x

3.Найти уравнение, равносильное уравнению
-2x + 5 = 3 – 4x

4.Найти выражение,
равное выражению
-2( -3x + 2y -4)

5.Работа в парах

Ребята, а вы помните, когда первый раз решали уравнения?

А вы знаете, кто и когда придумал первое уравнение?

Ответить на этот вопрос невозможно. Ещё за 3-4 тысячи лет до н.э египтяне и вавилоняне умели решать простейшие уравнения. Греки унаследовали знания египтян, и пошли дальше. Наибольших успехов в развитии учения об уравнениях достиг греческий учёный Диофант (3 век), о котором писали:

Он уйму всяких разрешил проблем.

И запахи предсказывал, и ливни

Поистине, его познанья дивны.

В дальнейшем многие математики занимались проблемами уравнений. Одним из них был французский математик, фамилию, которого вы узнаете, если выполните задания, предложенные вам для работы в парах.

Каждому корню уравнения соответствует буква из таблицы.

Решите уравнение:

1) 6х – 12 = 5х

2) -2х + 3 = 5х – 4

3) 7у – 7 = 5у + 3

4) -4а + 8 = -5а + 4

Ответ: Виет

Учащиеся обмениваются тетрадями, проверяют по эталону на слайде.

Проверка

Ответ: Виет

Франсуа Виет (1540-1603)

Замечательный французский математик, положивший начало алгебре как науке о преобразовании выражений, о решении уравнений в общем виде, создатель буквенного исчисления.

Физкультминутка:

Быстро встали, улыбнулись,

выше-выше потянулись!

Вправо, влево повернулись,

рук коленями коснулись.

На носки, затем на пятки.

Лень отбросить и опять

Сесть за парту, взять тетрадку уравнения решать!

6.«Ромашка»

Учащимся предлагается решить уравнения, которые записаны на лепестках ромашки. Ответ зашифрован буквой. Расшифруйте.

1) 3х + 45 = 2х + 15, х=-30

2) – 8х = — 8, х=1

3) 2х – 3 = 5, х=4

4) 3х + 1 = х + 3, х=1

5) 3х = — 18, х=-6

6) 5х + 4 = х – 12, х=-4

7) 7х + 3 = 3х + 11, х=2

8) – 7х = 21, х=-3

9) 3х – 8 = 2х – 1, х=7

10) 32х = — 16, х=-0,5

11)4х-50=6-3х, х=8

12) 9х – 5 = х – 5, х=0

13) 10х — 25 = 7х + 5, х=10

14) 4х + 7 = 11, х=1

15) 8х + 7 = 5х + 4, х=-1

16) 8х – 5 = 10х + 3, х=-4

17) 2у – 3 = 3у – 1, х=-2

18) 7у + 9 = 3у – 7, у=-4

19) 2у + 4 = у + 6, у=2

20) 16х = — 48, х=-3

Торопись – да не ошибись. Ребята открывают ответы и составляют пословицу. Хором читают мудрую мысль.

V. Домашнее задание.

Повторить правила п.30,31

№849 стр.181

Подготовиться к контрольной работе.

Итог урока.

Спасибо за работу.

Решение уравнений в 6 классе

Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа № 6

СЕКЦИЯ МАТЕМАТИКИ

Проектно-исследовательская работа на тему:

«Решение уравнений в 6 классе»

Исследователь : Жугина Анна

6 «Б» класс

Руководитель: Никитенко Ольга

Николаевна

Учитель математики

г.Красный Сулин

2017 г.

Оглавление

стр.

Введение…………………………………………………………………3

Историческая справка…………………………………………………..5

Методы решения уравнений……………………………………………7

Заключение………………………………………………………………13

Список использованных ресурсов……………………………………..14

Введение.

Как известно математика — это наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов. 

В школьном курсе математика представлена таким разделом как: арифметика, алгебра, геометрия, тригонометрия и начала анализа. Большую часть школьной математики занимает алгебра. Ее элементы начинают изучать уже в начальной школе (равенства, простейшие уравнения, неравенства) и продолжаются до 11 класса до логарифмических, показательных и дифференциальных уравнений.

Самый большой материал, который рассматривают на протяжении всех лет изучения алгебры – это различные уравнения и способы их решения. Уравнения уже сами по себе представляет интерес для изучения, так как в известном смысле именно с их помощью на символическом языке записываются важнейшие задачи, связанные с познанием реальной действительности, очевидно, что роль уравнений в естествознании определяет и их роль в школьном курсе математики. Большое значение в алгебре играет метод уравнений в решении задач жизненного содержания: это задачи, связанные с основами современного производства, экономика народного хозяйства, задач в смежных дисциплинах (физики, химии, биомеханики, астрономии и т.д.) Целью являются изучение истории возникновения уравнений, понятия решения уравнений и виды их упрощения, а также рассмотрение способов решения ряда занимательных задач с помощью уравнений.

Актуальность: чтобы перейти к исследованию данной темы, нам необходимо было ответить на вопрос: «Зачем нужно изучать уравнения?», и познакомить учащихся 6 класса с новой темой — перенос слагаемых из одной части уравнения в другую и свойства уравнений. Этот материал в курсе математики -6 рассматривается позже .

Проблема: углубить представления об уравнениях. Ответить на вопрос: «Как решить уравнения: 4х – 8 = 6 — 3х , (х — 3) : 4 = 6 и дробными коэффициентами?» Показать где, когда и какие уравнения приходится решать современному человеку.

Данная работа является попыткой обобщить и систематизировать изученный материал и изучить новый. В проект включены уравнения с переносом слагаемых из одной части уравнения в другую и с применением свойства уравнений, так же задачи, решаемые уравнением и дополнительный материал.

Математика… выявляет порядок,

симметрию и определенность,

а это – важнейшие виды прекрасного.

Аристотель.

Историческая справка

Представим, что в очень легком – практически невесомом – кошельке содержится какое-то количество монет одинакового достоинства. Как узнать, сколько монет в кошельке, не заглядывая внутрь? Есть очень простой способ: положим кошелек на одну чашу рычажных весов и уравновесим его монетками на другой чаше. Сколько монет для этого потребуется – столько же их и в кошельке.

В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. «Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37…», — поучал во II тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.

Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.

Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого трактата – «Китаб аль-джебер валь-мукабала» («Книга о восстановлении и противопоставлении») – со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.

Методы решения уравнений

Что такое уравнение?

Существуют уравнение в правах, уравнение времени (перевод истинного солнечного времени в среднее солнечное время, принятое в общежитии и в науке; астр.) и т.д..

В математике – это математическое равенство, содержащее одну или несколько неизвестных величин и сохраняющее свою силу только при определенных значениях этих неизвестных величин.

В уравнениях с одной переменной неизвестное обычно обозначают буквой «х».

Уравнения бывают разных видов:

Существуют такие способы решения уравнений как: алгебраический, арифметический и геометрический. Рассмотрим алгебраический способ.

Решить уравнение — это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное равенство или доказать, что решений нет. Решение уравнений, пусть это и сложно, захватывает нас. Ведь это, действительно, удивительно, когда от одного неизвестного числа зависит целый поток чисел.

В уравнениях для нахождения неизвестного надо преобразовать и упростить исходное выражение. Причем так, чтобы при смене внешнего вида суть выражения не менялась. Такие преобразования называются тождественными или равносильными. Сейчас мы с вами рассмотрим решение уравнения из учебника для 6 класса из раздела повторения уравнений за 5 класс. Задание 206, уравнение «а».

(х + 36,1) ^. 5,1 = 245,82

х + 361= 245,82 : 5,1

х + 36,1= 48,2

х = 48,2 – 36,1

х = 12,1

_____________________

Ответ: х = 12,1

Значение переменной, обращающее уравнение в верное равенство называется корнем уравнения.

Выполнив проверку получим:

(12,1 + 36,1) ^. 5,1 = 245,82

12,1 + 36,1 = 48,2

48,2 · 5,1 = 245,82

245,82 = 245,82

Значит 12,1 – корень уравнения.

Таким способом решают уравнения учащиеся до 6-ого класса. А в 6-ом классе они знакомятся с новым способом решения уравнении, таким как перенос слагаемых из одной части уравнения в другую. При этом знак слагаемых меняется на противоположный и применяют свойства уравнений – обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение. Рассмотрим решение уравнений с отрицательными числами. Возьмём пример №1341 «а»:

–20 · (х – 13) = – 220

[–20 · (х –13)] : [–20] = –220 : [– 20]

Х –13 = 11

Х = 11 + 13

Х = 24

Мир уравнений очень богат. При помощи них можно решить самые сложные задачи. С помощью уравнений в задачах мы находим связь между величинами, получаем опыт применения математики к решению практических задач.

Решение задач на проценты – в медицине, криминалистике, биохимии и т.д.

Бухгалтерские расчеты.

Решение уравнений применяется в строительстве (дороги, мосты и т.д.), архитектуре. При составлении прогноза погоды, геологии и т.д. В построении графика годового цикла состояния человека.

Рассмотрим некоторые из них, которые можно применить на уроках математики или на занятиях математического кружка.

Уравнение – это не только сухой математический термин, это язык алгебры!

«Чтобы решить вопрос, относящийся к числам или отвлеченным отношениям величин, нужно лишь перевести задачу с родного языка на язык алгебраический», — писал великий И. Ньютон в своем учебнике алгебры, который называется «Всеобщая арифметика». Под алгебраическим языком понимают язык уравнений и неравенств. Большинство текстовых задач решается именно этим способом. Посмотрим на примере, как выполняется такой перевод с родного языка на алгебраический.

Жизнь Диофанта.

В III—IV веках нашей эры жил в городе Александрии знаменитый греческий математик Диофант. До нас дошли шесть из тринадцати книг «Арифметики», написанных Диофантом. История сохранила нам мало черт биографии замечательного древнего математика Диофанта. Все, что известно о нем, почерпнуто из надписи на его гробнице — надписи, составленной в форме математической задачи. Эта надпись дает возможность определить продолжительность жизни математика, которого позднее назвали «отцом греческой алгебры». Надпись эта в переводе, подражающем древним стихам, такова:

Х

Часть шестую его представляло
прекрасное детство.

х

Двенадцатая часть протекла еще жизни –
покрылся пухом тогда подбородок.

х

Седьмую в бездетном браке
провел Диофант.

х

Прошло пятилетие;
он был осчастливлен рождением
прекрасного первенца сына.

5

Коему рок половину лишь
жизни прекрасной и светлой
дал на земле по сравненью с отцом.

х

И в печали глубокой
старец земного удела конец воспринял,
переживши года четыре
с тех пор, как сына лишился.

4

Скажи, сколько лет жизни достигнув,
смерть воспринял Диофант?»   

Приведем условие к уравнению. 
Вся жизнь принимается за х
Прекрасное детство:  х
Юность:  х
Бездетный брак:  х
Прошло пятилетие: 5
Половина жизни прекрасной:  х

Переживши года четыре: 4

Составим уравнение:

х + х + х + 5 + х + 4 = х

х + х + х + х – х = – 9

= – 9

– х = – 9

х = 84

Решив уравнение и найдя, что х=84, узнаем следующие черты биографии Диофанта; он женился в возрасте 21года, стал отцом на 38 году, потерял сына на 80 году и умер, достигнув возраста 84 лет.

Решение уравнений – зачастую дело нетрудное; составление уравнений по данным задачи затрудняет больше. Искусство составлять уравнения действительно сводится к умению переводить «с родного языка» на «алгебраический». Для примера рассмотрим задачу № 652 из учебника:

«Масса винограда в первом ящике составляет массы винограда во втором ящике. Сколько килограммов винограда было в двух ящиках, если в первом ящике был 21 кг винограда?»

Решение:

Пусть: х кг будет количество во 2-ом ящике.

х = кг количество в 1-ом ящике.

Всего 21 кг винограда.

Составим уравнение:

х + х = 21

1 х = 21

х =21 : 1

х =11

_________________

Ответ: 11 килограммов винограда было в двух ящиках.

Заключение

• При работе над проектом я узнала много нового и полезного из области математики.

• Познакомилась с биографией великих математиков.

• Узнала о том, где применяется решение уравнений в жизни современного человека.

Список используемых ресурсов:

1. Виленкин Н. Я. «Математика 6 класс». Издательство Мнемозина, Москва. 2013.

2. Бекаревич А.Н «Уравнения в школьном курсе математики» 1968.  Минск, Народная Асвета

3. Мордкович А. Г. «Школа абитуриента. Научись сам. Решаем уравнения» Шкала-Пресс, 1995

4. Я.И. Перельман «Занимательная алгебра». Москва «Наука» 1978 г

5. www.proshkolu.ru.

6. www.1september.ru

Свойства уравнений (6 класс)

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа № 55

г. Нижний Тагил Свердловской области

Конспект урока по математике в 6 классе

Решение уравнений

подготовила

учитель математики и информатики

Серебренникова Елена Владимировна

г. Нижний Тагил

2017

Решение уравнений

Предмет Математика

Класс 6В

Время 1 урок (40 мин)

Тип урока: формирование новых знаний.

Формы, методы, приѐмы работы: самостоятельная работа, фронтальная беседа, работа учащихся в группах с кейсом.

Тип кейса: обучающий.

Ресурсы: раздаточный материал – кейсы.

Цель: формирование умения у учащихся умение решать уравнения.

Задачи:

1. Формирование навыка решения уравнений.

2. Формирование умения осуществлять самоконтроль в процессе самостоятельной работы.

3. Развитие умения анализировать, систематизировать, интерпретировать полученные результаты.

4. Воспитание умения работать в команде; умения критически относиться к мнению одноклассников.

Для решения проблемы подготовлен кейс, в котором предложена информация о линейном уравнении, его свойствах, алгоритм решения. Учащиеся должны ознакомиться с предложенной информацией и, опираясь на нее, выполнить задание.

Работа с кейсом.

Обучающимся озвучивается тема занятия «Решение линейных уравнений» и проговаривается о том, что занятие будет проводиться в режиме кейс-метода.

Кейс предоставляется ученикам непосредственно на занятии. На его изучение, ознакомление с ним отводится около 10 минут времени занятия.

Затем организуется работа в группах по поиску решения поставленной проблемы. Учитель консультирует учеников, ученики в группах обсуждают варианты, объясняют непонятные моменты друг другу. Данный этап занятия длится около 10 минут.

На следующем этапе организуется обсуждение вариантов решений групп, что занимает по времени около 12 минут с учетом обсуждения предложенных решений.

Итоговая часть занятия занимает около 8 минут и посвящена подведению итогов, обобщению полученных результатов, заполнению карты самоанализа. Итоговую часть занятия проводит учитель, опираясь на презентованные группами варианты решений.

Кейс «РЕШЕНИЕ УРАВНЕНИЙ»

До сегодняшнего урока мы не умели решать уравнения, в которых неизвестное находилось слева и справа от знака равенства: 3x+7=x+15. Некоторые из вас постоянно забывают правила нахождения неизвестного слагаемого, уменьшаемого, вычитаемого. Сегодня мы постараемся разрешить эти затруднения.

Решить уравнение – значит найти все его корни (или убедиться, что это уравнение не имеет ни одного корня).

Уравнения обладают свойствами:

1. Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.

2. Корни уравнения не изменяются, если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.

Пример:

6х-12=4х+4

6х-4х=4+12

2х=16

2х:(2)=16:(2)

х=8

6*8-12=4*8+4

36=36

Ответ: х=8

Уравнение, которое можно привести к виду ax=b, где a и b − некоторые числа (a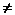0), называется линейным уравнением с одним неизвестным.

Задание для самостоятельной работы

Решить уравнения:

1. -9а+8=-10а-2

2. 7m+1=8m+9

3. 

Алгоритм решения линейного уравнения

Шаг 1

Раскрываем скобки (если нужно)

Шаг 2

Все члены содержащие неизвестное переносим в левую часть, а не содержащие неизвестное − в правую.

Шаг 3

Приводим подобные слагаемые.

Шаг 4

Делим обе части уравнения на коэффициент при неизвестном.

 Шаг 5

Записываем ответ.

Задание группам

Группа1

1. Составить алгоритм решения уравнений.

2. Решить уравнение:

0,5х+3=0,2х

3. Представить результаты работы.

Группа 2

1. Составить алгоритм решения уравнений.

2. Решить уравнение:

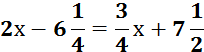
3. Представить результаты работы.

Группа 3

1. Составить алгоритм решения уравнений.

2. Решить уравнение:

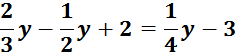
3. Представить результаты работы.

Группа 4

1. Составить алгоритм решения уравнений.

2. Решить уравнение:

4,7-8z=4,9-10z

3. Представить результаты работы.

Группа 5

1. Составить алгоритм решения уравнений.

2. Решить уравнение:

6,9-9n=-5n-33,1

3. Представить результаты работы.

Группа 6

1. Составить алгоритм решения уравнений.

2. Решить уравнение:

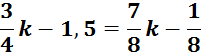
3. Представить результаты работы.

Вопросы для обсуждения по материалам кейсов.

1. Обсудите в группах результаты исследования.

2. В итоге каждая группа выступает с предложениями по решению задачи.

3. Обсуждение результатов исследования работы в группах.

Выработка рекомендаций по результатам работы.

Карточка для самооценки

Фамилия, имя учащегося____________________________________________________

Выполнил самостоятельно

Исправил

при работе в группе

Не выполнил

Уравнение 1

Уравнение 2

Уравнение 3

Оцените свою работу в группе (от 0 до 3 балла):

Участие в презентации деятельности группы (0-3 балла):

Список использованной литературы

1. Виленкин Н.Я. и др. Математика 6 класс – М.: «Мнемозина», 2012.

2. Выговская В.В. Поурочные разработки по математике – М.: «ВАКО», 2012.

Урок математики «Уравнения», 6 класс

 Огрызко Ирина Владимировна,

учитель математики, МБОУ СОШ №2 г. Донецка

Предмет: математика

Класс: 6

Тема урока: Уравнения

Базовый учебник: И.И. Зубарева, А.Г. Мордкович, Математика: 6 класс: учебник для учащихся общеобразовательных учреждений / М: Мнемозина, 2014 – 264 с.

Тип урока: урок «открытия» нового знания (45 минут)

Целевые установки на достижение планируемых результатов:

— личностные: умение слушать и вступать в диалог, участвовать в обсуждении проблем, содействовать формированию и развитию нравственных, трудовых, эстетических качеств личности учащихся (дисциплинированность, ответственность, аккуратность, радость и сопереживание их успехам), формировать коммуникативную компетенцию учащихся;

— метапредметные: способствовать развитию устной и письменной речи, изложению своих мыслей с применением математической терминологии, обогащению ее словарного запаса, самостоятельного мышления, навыка самооценки, самопроверки и ведения записей в собственной тетради;

— предметные: создать условия для понимания алгоритма решения уравнений и использования свойств уравнений.

Оборудование:

компьютер, экран, проектор, раздаточный материал, презентация.

ХОД УРОКА

 Приветствие учеников. Проверка готовности к уроку.

1) Продолжите предложения:

— коэффициентом называется….

— подобные слагаемые – это слагаемые, у которых …

— привести подобные слагаемые – это выполнить действия с коэффициентами ….

— чтобы число умножить на сумму (разность), нужно …

— если перед скобкой стоит знак минус, то ….

— если перед скобкой стоит знак плюс, то …

2) Установите соответствие между выражениями и заполните таблицу:

На доске в два столбика размещены выражения, ребята устанавливают соответствия между ними

Математический диктант (мультимедийное приложение к учебнику математики под редакцией И.И Зубаревой, п.18) с взаимопроверкой. По окончании ребята обмениваются тетрадями для проверки.

На слайде представлена таблица. На столе у обучающихся карточки с примерами и ответы.

Я предлагаю вам разгадать тему урока. Выполните вычисления в тетради, и в таблице напишите букву, соответствующую правильному ответу. Получившиеся слово – это тема урока. Я думаю, что вы справитесь с этим заданием за 4 минуты.

Раздаточный материал
 

Ребята по завершении времени называют буквы, соответствующие числам в таблице ( слайды 3 – 11).

Верно, мы получили слово «уравнение». Запишите в тетрадях тему урока: «Уравнения» (слайд 12).

5. Актуализация знаний.

1) С уравнениями вы знакомы с начальной школы. Давайте вспомним: (1 мин)

— что такое уравнение;

— что значит решить уравнение;

— что такое корень уравнения?

Звучат ответы обучающихся.

2) Историческая справка: (слайд 13) (2 мин)

Учитель знакомит учащихся с историей возникновения уравнений:

Первым руководством по решению задач с неизвестным, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда Бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого трактата — «Китаб аль-джебр Валь-мукабала» (» Книга о восстановлении и противопоставлении») — со временем превратилось знакомое всем слово «алгебра». А само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.

В сочинении аль-Хорезми неизвестные величины, так же как и все сопутствующие выкладки и преобразования уравнений, выражались словесно.

Такой стиль изложения, характерный для раннего этапа развития алгебры, историки науки называют риторическим (красноречивым).

Новый великий прорыв в алгебре связан с именем французского ученого XVI в. Франсуа Виета. Он первым из математиков ввел буквенные обозначения для коэффициентов уравнения и неизвестных величин. А традицией обозначать неизвестные величины последними буквами латинского алфавита (х, y или z) мы обязаны соотечественнику Виета — Рене Декарту.

3) Внимание на слайд! (слайд 14) (2 мин)

Перед вами уравнения. Выпишите в тетрадь те уравнения, которые вы не знаете, как решить. Что, именно, в выписанных уравнениях, вызывает у вас затруднение? Как решить остальные уравнения?

Обучающиеся выписывают уравнения №№2, 3, 5

4) Работа с алгоритмом.

Предлагаю вам познакомиться с алгоритмом решения таких уравнений. У вас на столе лежат карточки-консультанты, в которых представлен алгоритм решения уравнений и решенные примеры. Я предлагаю вам прочитать алгоритм и рассмотреть решенные примеры. На эту работу я отвожу вам 2 минуты. А теперь попробуем вместе решить уравнение.

Учитель у доски, ребята в тетрадях. С места, фронтально, пошагово читается алгоритм и проговаривается решение (ученики), а учитель записывает на доске. (3 мин)

Ребята, вы обратили внимание, что новое для вас правило (свойство уравнения) содержится в п.3 алгоритма. Чтобы вам было легче его запомнить предлагаю вам мнемонический прием:

• — При переносе слагаемых из одной части уравнения в другую, нужно поменять знаки тех слагаемых, которые мы переносим – когда мы идем в гости – мы переодеваемся.

  — Сначала записываем слагаемые, которые были в этой части уравнения (это – хозяин) – гости могут прийти, если хозяин дома (переодеваются только гости).

5. Первичное закрепление. (слайд 15) (15 мин)

Фронтально. Ученики по желанию у доски решают уравнения с использованием алгоритма.

а) 3 – 4х = 4х – 5;

б) 9(х + 7) = – х;

в) 10 – 3(1 – 7х) = –4х – 8.

г)

6. Рефлексия. (слайд 16) (5 мин)

Синквейн:

1-я строка – одно ключевое слово, определяющее содержание синквейна; (УРАВНЕНИЕ)

2-я строка – два прилагательных, характеризующих данное понятие; (ЛИНЕЙНОЕ, АЛГЕБРАИЧЕСКОЕ)

3-я строка – три глагола, обозначающих действие в рамках заданной темы; (РЕШАТЬ, УПРОЩАТЬ, ПЕРЕНОСИТЬ)

4-я строка – короткое предложение, раскрывающее суть темы или отношение к ней; (РЕШАТЬ УРАВНЕНИЕ ПО АЛГОРИТМУ)

5-я строка – синоним ключевого слова (существительное). (РАВЕНСТВО)

7. Итоги урока. Домашнее задание. (слайд 17) (3 мин)

§19, №580 (в, г), №582 (а, в), №585 (в, г)

Творческое задание: найти информацию и подготовить сообщение о способе решений уравнений, предложенном Мухаммеда Бен Мусы аль-Хорезми.

Используемые источники:

И.И. Зубарева, А.Г. Мордкович, Математика: 6 класс: учебник для учащихся общеобразовательных учреждений / М: Мнемозина, 2014 – 264 с.

И.И. Зубарева, Математика: 6 класс: мультимедийное приложение, п.18.

Шаблон презентации: http://ppt.znanio.ru/buy-now/

История возникновения уравнений http://mydocx.ru/3-94807.html

http://knowledge.allbest.ru/mathematics/3c0a65635a3bd78a5c53a89421216d37_0.html

раздаточный материал
PDF / 300.2 Кб
карточка-консультант «Алгоритм решения уравнений»
PDF / 252.23 Кб
математический диктант
PPT / 64.5 Кб
презентация к уроку «Уравнения»
PPTX / 1.7 Мб
урок «Уравнения», 6 класс
PDF / 571.74 Кб

Линейные уравнения в 6 классе

После простейших рассмотрим следующие линейные уравнения, решаемые в 6 классе, — уравнения вида ax+b=cx+d.

Алгоритм (план) решения таких линейных уравнений:

неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки.

Рассмотрим примеры решения таких линейных уравнений в 6 классе.

1) 5x-11=2x+7

Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

5x-2x=7+11

(Чтобы лучше запомнить это правило, предлагаю следующую ассоциацию. Есть хозяин, к нему пришел гость. Хозяин у себя дома, в своих домашних тапочках. Гостю надо снять обувь, в которой он пришел — не будет же он ходить в доме в обуви, в которой ходил по улице.

В левой части «хозяин» — слагаемое с переменной, 5x. Оно «у себя дома», поэтому его знак не меняем.  «В гости» к нему приходит из правой части уравнения 2x. Его знак меняем на противоположный. В левой части 2x имело знак «+», при переносе знак изменяем на «-«.

Аналогично, «хозяин» правой части — 7.  Его знак не меняем, так как это слагаемое остается в правой части. К нему из левой части «приходит в гости»  -11.  Его знак меняем на противоположный — был «-«, при переносе меняем его на «+».)

3x=18

Это — простейшее линейное уравнение. Обе части уравнения делим на число, стоящее перед иксом:

x=18:3

x=6

Ответ: 6.

2) 12 — 7x=16x + 3

Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

-7x-16x=3-12

-23x=-9

обе части уравнения делим на число, стоящее перед иксом:

x=-9:(-23)

При делении чисел с одинаковыми знаками получается положительное число. Поскольку 9 на 23 не делится, ответ записываем в виде обыкновенной дроби:

Ответ: 9/23.

3) 15x+11=10x-7

Это — линейное уравнение. Неизвестные переносим в одну сторону, известные — в другую с противоположными знаками:

15x-10x=-7-11

5x=-18

Обе части уравнения делим на число, стоящее перед иксом:

x=-18:5

При делении чисел с разными знаками получаем отрицательное число. При делении на 5 ответ записываем в виде десятичной дроби.

x=-3,6

Ответ: -3.6.

4) 54-3y=4y+72

Это — линейное уравнение. Неизвестные переносим в одну сторону, известные — в другую, изменяя при переносе их знаки:

-3y-4y=72-54

-7y=18

Обе части уравнения делим на число, стоящее перед игреком:

y=18:(-7)

При делении чисел с разными знаками получаем отрицательное число. 18 на 7 не делится, поэтому ответ записываем в виде обыкновенной дроби:

Эта дробь — неправильная. Выделяем из нее целую часть:

Ответ:

Позже рассмотрим, как решать в 6 классе более сложные линейные уравнения, в которых требуется раскрыть скобки и привести подобные слагаемые.