Онлайн урок: Решение уравнений по предмету Математика 6 класс
Решить линейное уравнение с одним неизвестным вида a ∙ x = b — это значит найти все его корни или доказать, что корней нет.
Наличие и количество корней линейного уравнения зависит от значений коэффициента а и значения свободного члена уравнения b.
1. Линейное уравнение при a ≠ 0 и b — любое число, будет иметь один единственный корень; это значит, что неизвестная имеет единственное верное решение, при котором уравнение обращается в верное равенство.
Известно, что деление — это обратное действие умножению (т.е. по известному множителю и произведению можно определить неизвестный множитель).
Следовательно, решение уравнения a ∙ x = b, где a ≠ 0 выглядит так:
x = b ÷ a
или \(\mathbf{x = \frac{b}{a}}\) (это корень линейного уравнения).
2. Линейное уравнение при a = 0 и b ≠ 0 не имеет корней.
Если коэффициент а равен нулю, линейное уравнение запишется, как
0 ∙ x = b
Свойство умножения числа на нуль дает право утверждать, что при любом значении неизвестной х уравнение обращается в неверное равенство 0 = b.
Равенство 0 = b при b ≠ 0 неверно, а это значит, что в таком случае решения уравнения нет, т.е. уравнение не имеет корней.
3. Линейное уравнение при а = 0 и b = 0 имеет бесконечное множество корней, т.е. при любом значении неизвестной х уравнение обращается в верное равенство.
0 ∙ x = 0
0 = 0 (верное равенство)
Чтобы решить линейное уравнение необходимо выполнить ряд математических преобразований.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Линейные уравнения обладают свойствами, которые позволяют совершать равносильные преобразования с различными уравнениями и сводить их к линейному уравнению с одной неизвестной стандартного вида, решать которое мы уже умеем.
Известно, что уравнение — это математическое равенство.
Если это равенство верно при определенных значениях неизвестной, то уравнение имеет верное решение.
Попробуем провести аналогию между уравновешенными весами и уравнением ax = b.
Как нам известно, уравновешенные весы нам показывают, что на каждой чаше весов находятся грузы равной массы.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Если весы были уравновешены, то добавив груз на одну чашу весов, необходимо добавить такой же по массе груз на вторую чашу, чтобы равновесие весов не было нарушено.
Аналогично, если убрать часть груза с одной чаши весов, то такую же часть груза нужно убрать со второй чаши, чтобы весы оставались уравновешенными.
А сейчас представим, что левая чаша весов — это левая часть линейного уравнения (ах), правая чаша весов — свободный член этого уравнения (b).
В таком случае получается, что если к левой и правой части уравнения прибавим (отнимем) одно и тоже число, то верное равенство не нарушится — получается уравнение равносильное исходному.
Добавлять к исходному можно любые числа, но необходимо выбирать то, которое упростит уравнение.
Рассмотрим пример:
Дано линейное уравнение 5х + 12 = 37
Для того, чтобы привести данное уравнение к стандартному виду: ax = b, прибавим к левой и правой части равенства —12 (противоположное числу 12, которое находится в правой части равенства, чтобы избавится в правой части от свободного члена уравнения),
5х + 12 + (-12) = 37 + (-12)
5х + 12 — 12 = 37 — 12
5х = 37 — 12
Если посмотреть внимательно на решение, то можно заметить, что число +12 исчезло из левой части исходного уравнения и появилось в правой части полученного после преобразований, при этом сменило знак и стало равным —12.
5х = 25 получили уравнение вида ax = b, так как a ≠ 0 и b ≠ 0 уравнение имеет единственный корень, найдем его:
х = 25/5
х = 5
Ответ: х = 5
Первое свойство равносильного преобразования уравнения
Любое слагаемое можно перенести из одно части уравнения в другую, при этом сменив знак этого слагаемого на противоположный, в результате получится новое уравнение, равносильное исходному.
Обычно слагаемые с неизвестным переносят в левую часть уравнения, а все остальные слагаемые в правую часть.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Рассмотрим второе свойство равносильного преобразования уравнения.
Снова обратимся к аналогии с весами.
Для того, чтобы весы оставались в равновесии, увеличивая массу груза в 1,5 раза в одной из чаш, необходимо увеличить массу груза в 1,5 раза в другой чаше весов.
Увеличивая или уменьшая массу грузов на каждой чаше весов в одинаковое количество раз, равновесие весов будет сохраняться.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Так же происходит и с уравнением. Сформулируем второе свойство равносильного преобразования уравнения:
Разделив (или умножив) обе части на одно и тоже ненулевое число, равенство остается верным, получится уравнение равносильное исходному.
Рассмотрим пример
Дано уравнение 4 ∙ (2х — 1) = 16
Приведем данное уравнение к стандартному виду: ax =b
Раскрытие скобок только усложнит исходное уравнение.
Заметим, что левую и правую часть можем разделить на 4 (это наименьшее общее кратное чисел 4 и 16).
4 ∙ (2х — 1) = 16 |÷4
\(\mathbf{\frac{4 \cdot (2x — 1)}{4} = 16 \div 4}\)
2х — 1 = 4
Слагаемые с неизвестным оставляем в левой часть уравнения, а слагаемое -1 переносим в правую часть уравнения, сменив знак числа на противоположный, т.е. на «+».
2x = 4 + 1
2x = 5 получили уравнение вида ax = b
х = 5/2
x = 2,5
Ответ: х = 2,5
Решение линейных уравнений происходит с помощью нескольких преобразований, которые могут быть выполнены в любом порядке.
1. Освобождение от дробных членов уравнения (если такие есть) с помощью умножения левой и правой части уравнения на одно и тоже ненулевое число
2. Деление левой и правой части уравнения на одно и тоже ненулевое число
3. Раскрытие скобок (если они есть и это необходимо)
4. Перенос членов уравнения из одной части в другую со сменой их знаков на противоположные
5. Приведение подобных слагаемых
Завершая решение уравнения, стоит выполнить проверку, подставив в исходное уравнение найденное значение неизвестного. Если уравнение обратилось в верное равенство, значит, корень уравнения найден верно.
Итогом решения уравнения является ответ, в котором перечисляются все найденные корни уравнения.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Конспект урока по математике «Решение уравнений» (6-й класс)
Цели:
Образовательные:
- повторить правила, которыми пользуются при
решении уравнений; - ознакомить со свойствами уравнений и новым
способом решения уравнений; - выработка умений решать уравнения с
применением их свойств.
Развивающие:
- развитие интереса к предмету на базе получения
новой информации, грамотной математической речи,
творческих способностей.
Воспитательные:
- воспитание культуры общения.
Оборудование: доска, экран, проектор,
компьютер.
Дидактические средства:
- математика-6 (Н. Виленкин и др.) АО “Московские
учебники” Москва 2007 - рабочие листы.
- компьютерная презентация. Использованы
рекомендации по применению ЦОП к учебникам И.И.
Зубаревой, А.Г.Мордковича “Математика, 6 класс”
Тип урока: урок усвоения новых знаний.
Ход урока
I. Организационный момент
Обращаю внимание учащихся на тот факт, что у
каждого из них на столе лежит рабочий лист с
заданиями, выполнение которых будет проходить
поэтапно, в течение всего урока.
II. Сообщение темы урока
Тема записывается на доске и в тетрадях.
Краткая информация о значимости данной темы.
III. Изучение нового материала
Подготовительная работа.
- Умеем ли мы решать уравнения? (Да)
По какому правилу решаем уравнения? (По правилу
отыскания неизвестного множителя)
Как найти неизвестный множитель?
- Выполните задание № 1 рабочего листа. Можно
предложить несколько вариантов рабочих листов.
- Проверим по вариантам задание под буквой б).
Есть ли ошибки? Оказывается, есть.
Выписываю на доске уравнение: -9 х = -3. Находили х
по правилу нахождения неизвестного множителя, х =
1/3. Нельзя ли придумать другое правило для
нахождения х? Попробуем. Умножим обе части
уравнения на – 1/9, получим – 1/9 (-9)х = -3(– 1/9), х = 1/3.
Результат тот же. Случайно ли это? Давайте
проверим.
Возвращаемся к уравнениям презентации и
несколько уравнений решаем предложенным
способом. Ответы получаем те же, но быстрее. Мы
умножали обе части на одно и то же число, не
равное нулю. А нельзя ли разделить? Оказывается,
можно.
Делаем вывод и формулируем первое свойство
уравнений. Читаем его по рабочему листу.
При решении уравнений важно уметь приводить
подобные слагаемые.
Выполним упражнение в тетрадях. Записываем
только ответы.
(Презентация), <Рисунок 3>
IV. Физкультминутка, совмещенная с игрой
Как вы заметили, в рабочем листе записано еще
одно свойство уравнений. Нам надо его изучить.
Проведем подготовительную работу. Объявляю игру
“ В каждой шутке есть доля правды”. Собираясь с
родителями за границу на отдых, вы прежде всего
позаботитесь о чем? (о заграничном паспорте).
Переехал границу – меняй паспорт.
На доске записаны три уравнения, знак = означает
“границу”. Некоторые слагаемые перенесены
через “границу”, но все ли сделано верно?
х – 7,2 = -7,3
х = – 7,3 – 7,21,8 – х = 1,9
1,8 – 1,9 = х12х – 13 = 8х – 9
12х – 8х = -13 – 9
Если переход через границу законный, наклоните
медленно головы вперед; если переход осуществлен
“без паспорта”, наклоните головы назад. (По
каждому уравнению спрашиваю учеников отдельно)
Хорошо. Шутки сейчас закончены, но доля правды
останется.
V. Продолжаем изучение темы
По учебнику решаем пример № 3: 5х = 2х + 6.
(Внимательно изучите рисунок). Весы находятся в
равновесии. Масса одного батона х кг, убираем по
два батона с каждой чашки, тогда уравнение
перепишем:
5х – 2х = 2х + 6 – 2х,
5х – 2х = 6, сравните полученное уравнение с
первоначальным: слагаемое 2х было в правой части
уравнения, а сейчас оно в левой части, но с
противоположным знаком.
3х = 6,
х = 2.
Вывод. Корни не изменяются, если какое-то
слагаемое перенести из одной части уравнения в
другую, поменяв при этом знак. Прочитали правило
по рабочему листу.
Самостоятельно выполнить № 2 рабочего листа.
Выполняем на доске и в тетрадях №№ 1316(а, б, в, г).
А сейчас решим уравнения, в которых применяются
оба свойства одновременно: № 1317 (а, г).
Проговорили алгоритм решения уравнений (Презентация),
<Рисунок 4 >
Выполнить № 1318 (а, в). Самостоятельно выполнить
№ 3 рабочего листа.
Выполняя задания, мы все уравнения сводили к
виду ах = в, где а ? 0. Такое уравнение называется
линейным уравнением.
Выполните № 4 рабочего листа.
VI. Итог урока
Что называется уравнения?
Что называется корнем уравнения?
Что значит решить уравнение?
Что нового было на уроке? (Свойства уравнений)
Сформулируйте свойства уравнений.
Выставление оценок за урок.
В завершение слова Альберта Эйнштейна: “Мне
приходится делить время между политикой и
уравнениями. Однако уравнения, по-моему, гораздо
важнее. Политика существует только для данного
момента, а уравнения будут существовать вечно”.
VII. Рефлексия
Если вы все поняли, вам было интересно,
изобразите в правом углу рабочего листа «сердечко»
Если материал усвоен плохо, есть проблемы, то
нарисуйте грустное личико.
Рабочий лист (образец) (См. Приложение
2)
Индивидуальное домашнее задание по математике на тему «Решение уравнений» (6 класс)
Индивидуальная работа по теме: «Решение уравнений».
1.
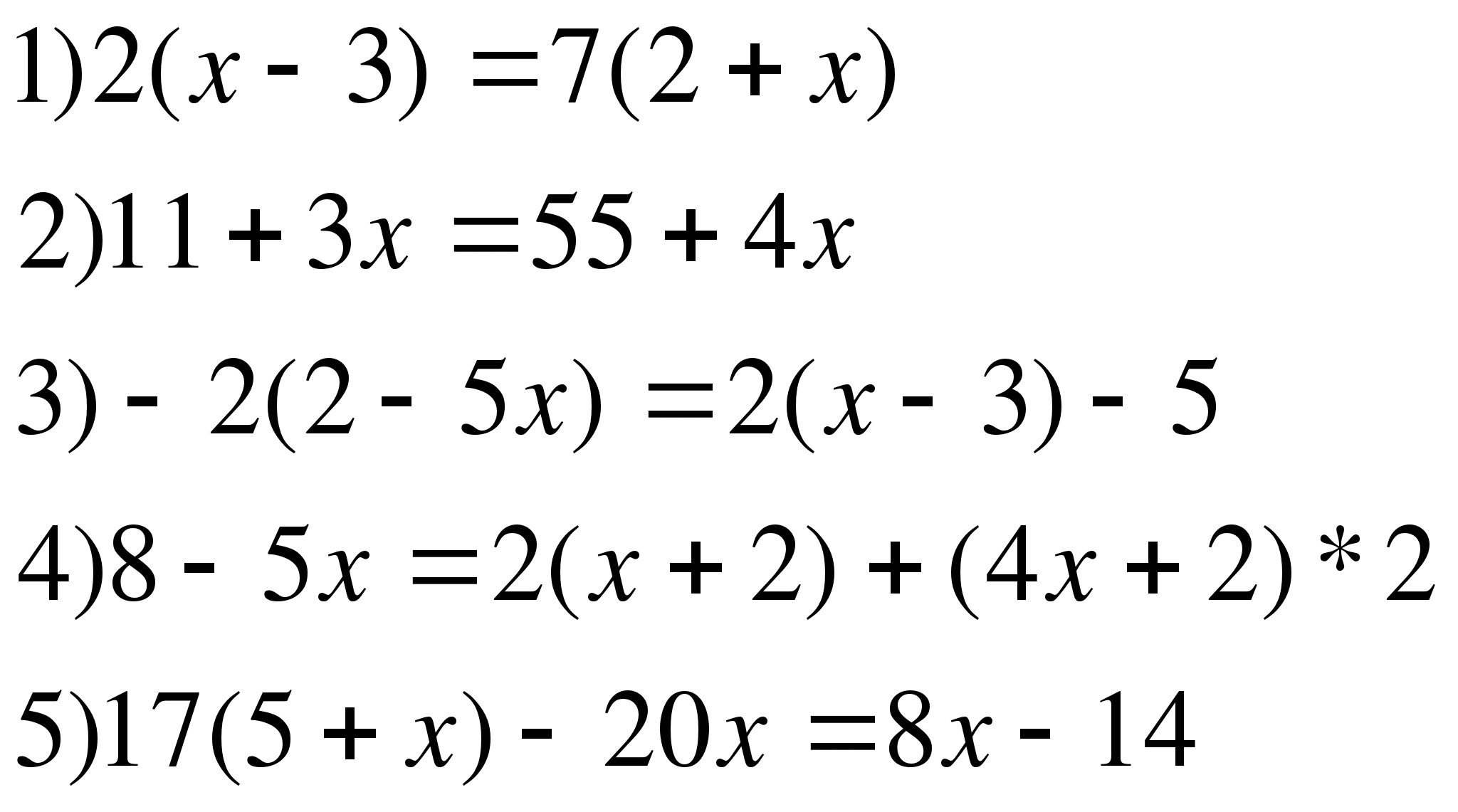
2.
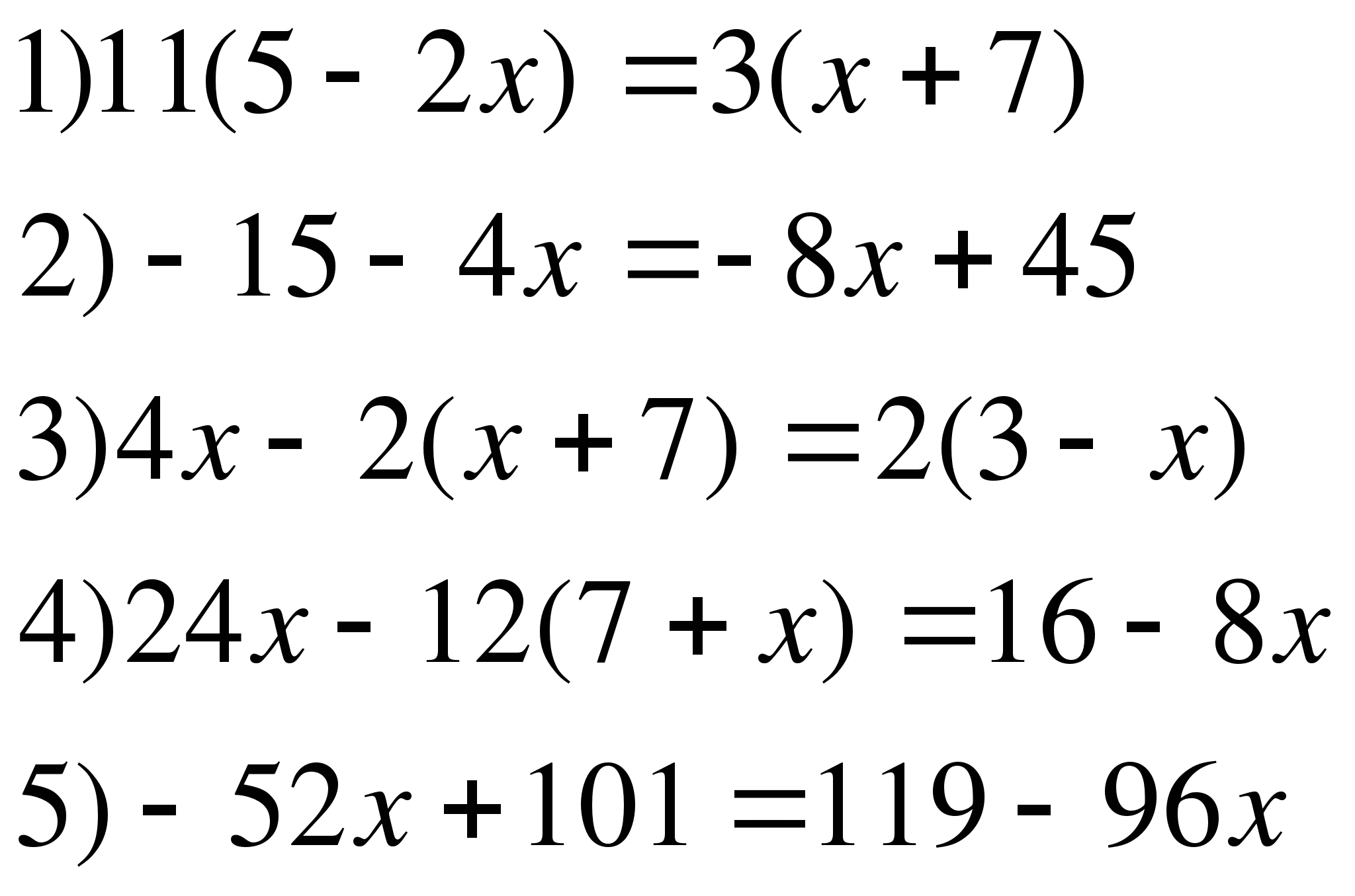
3.
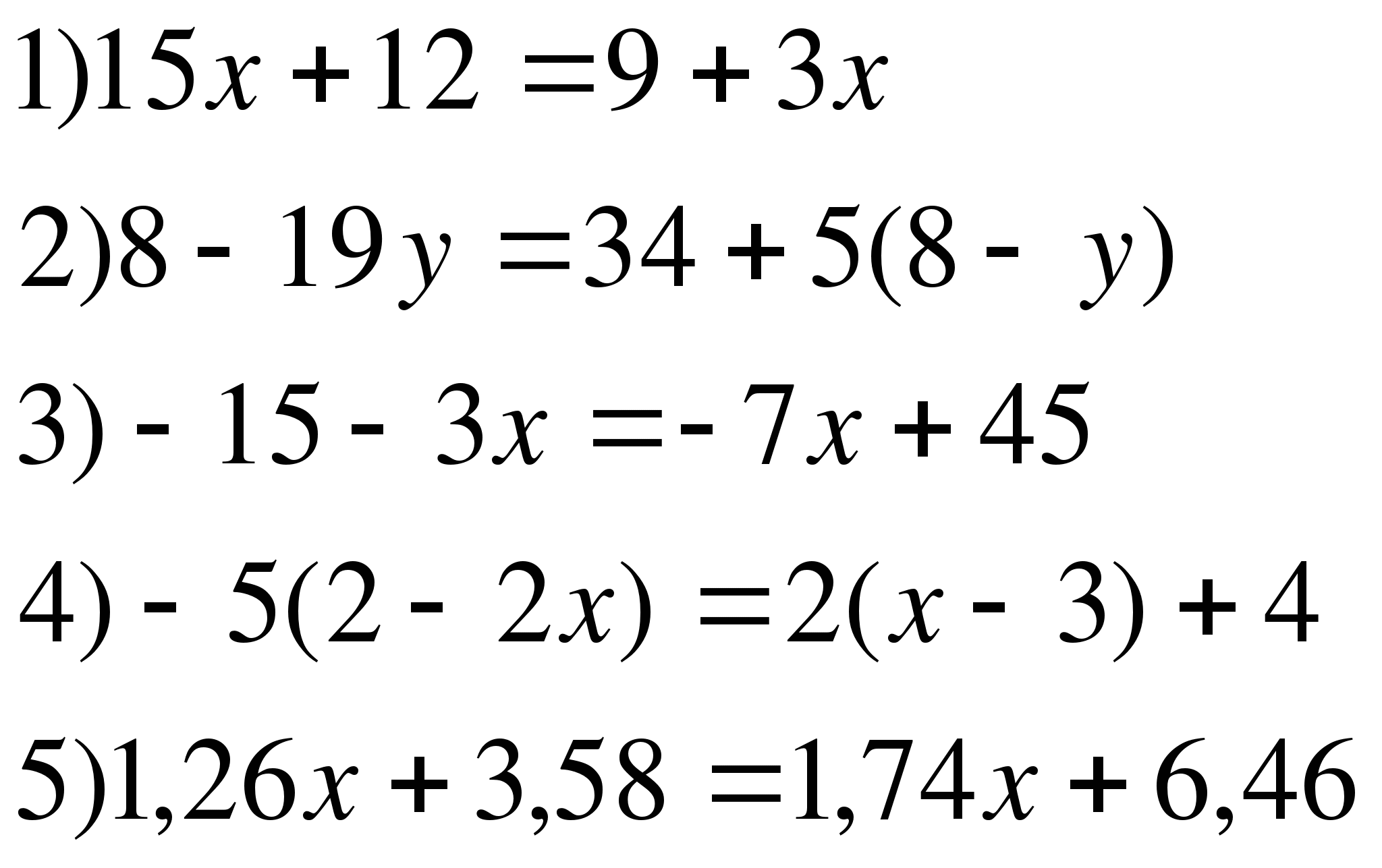
4.
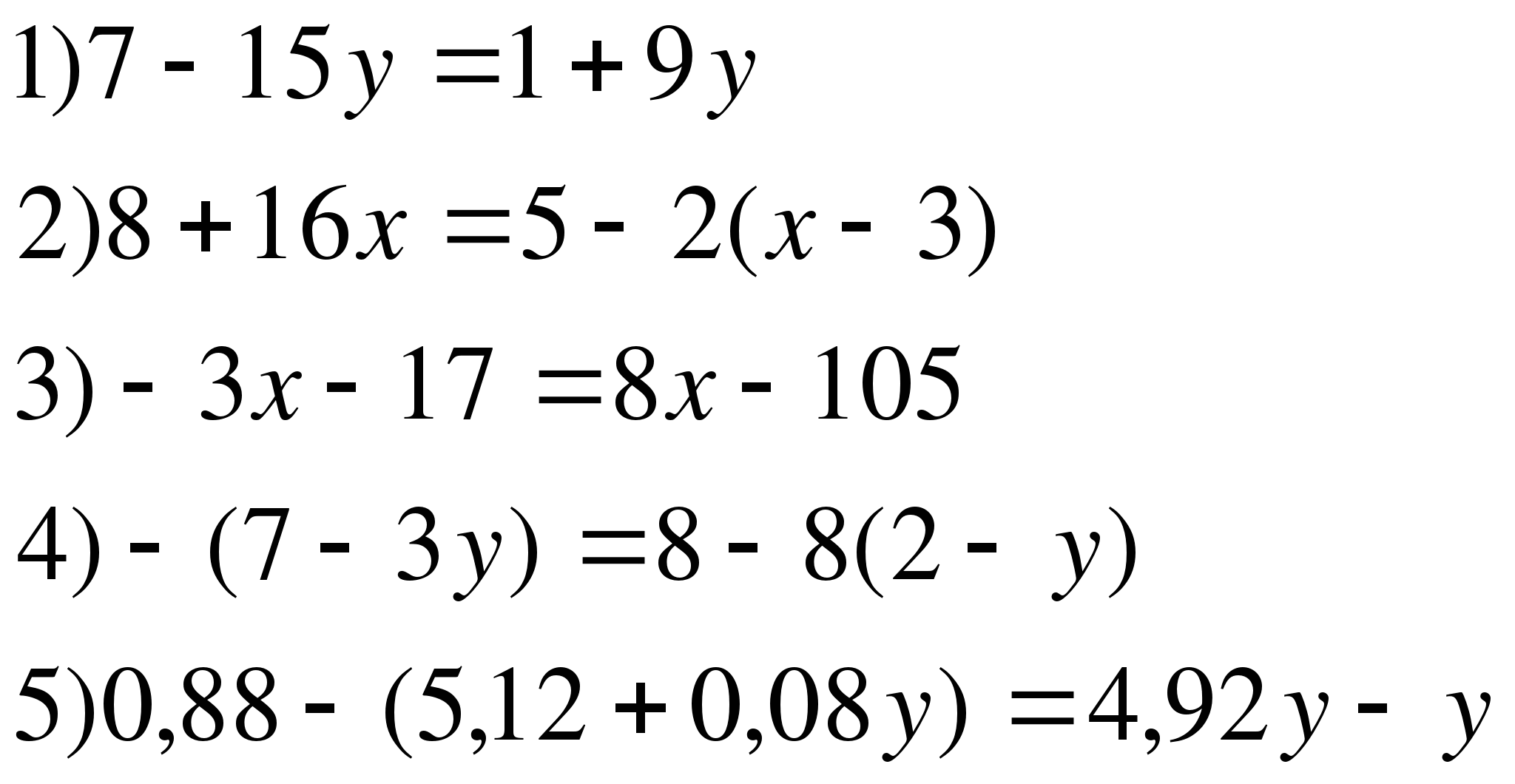
5.
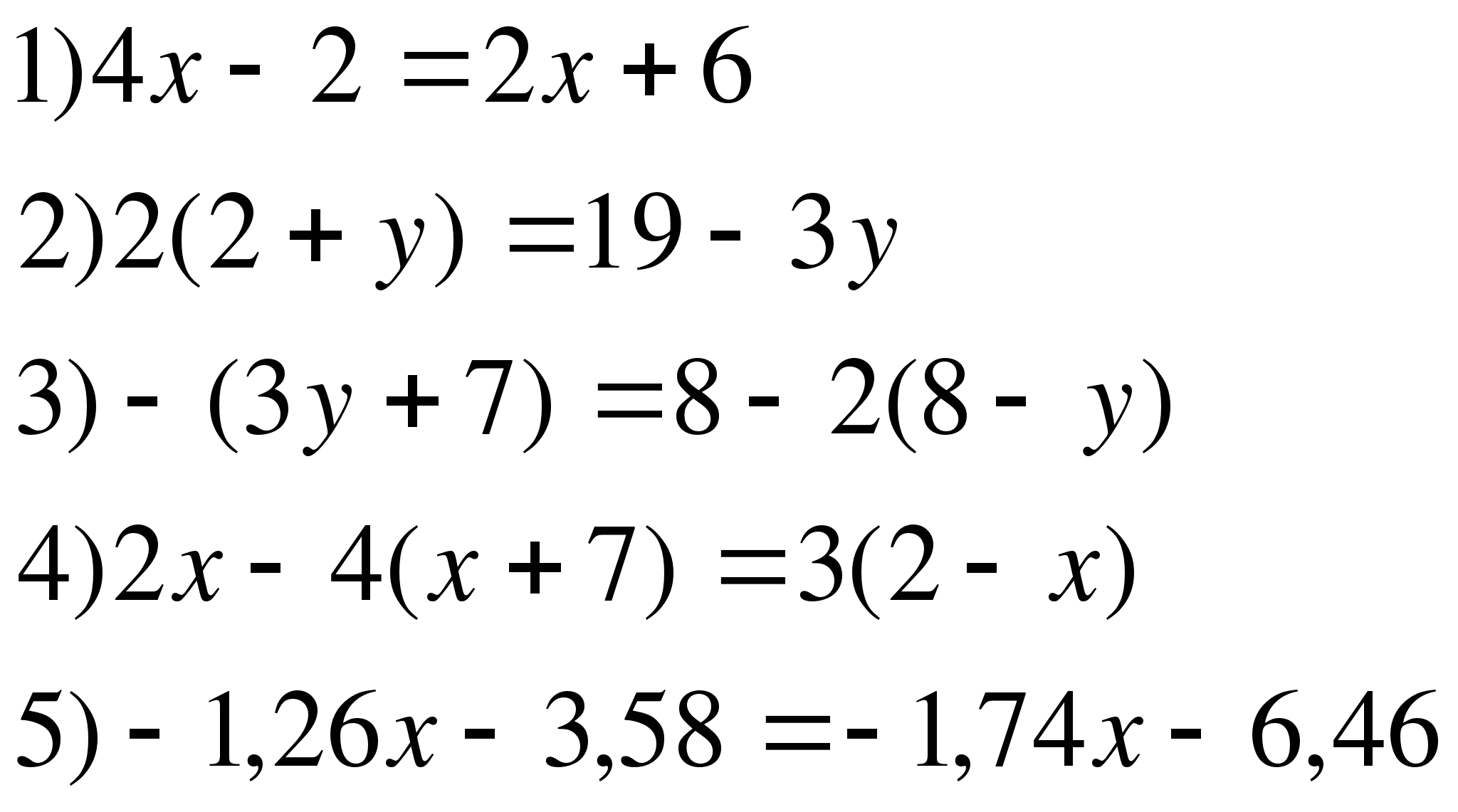
6.
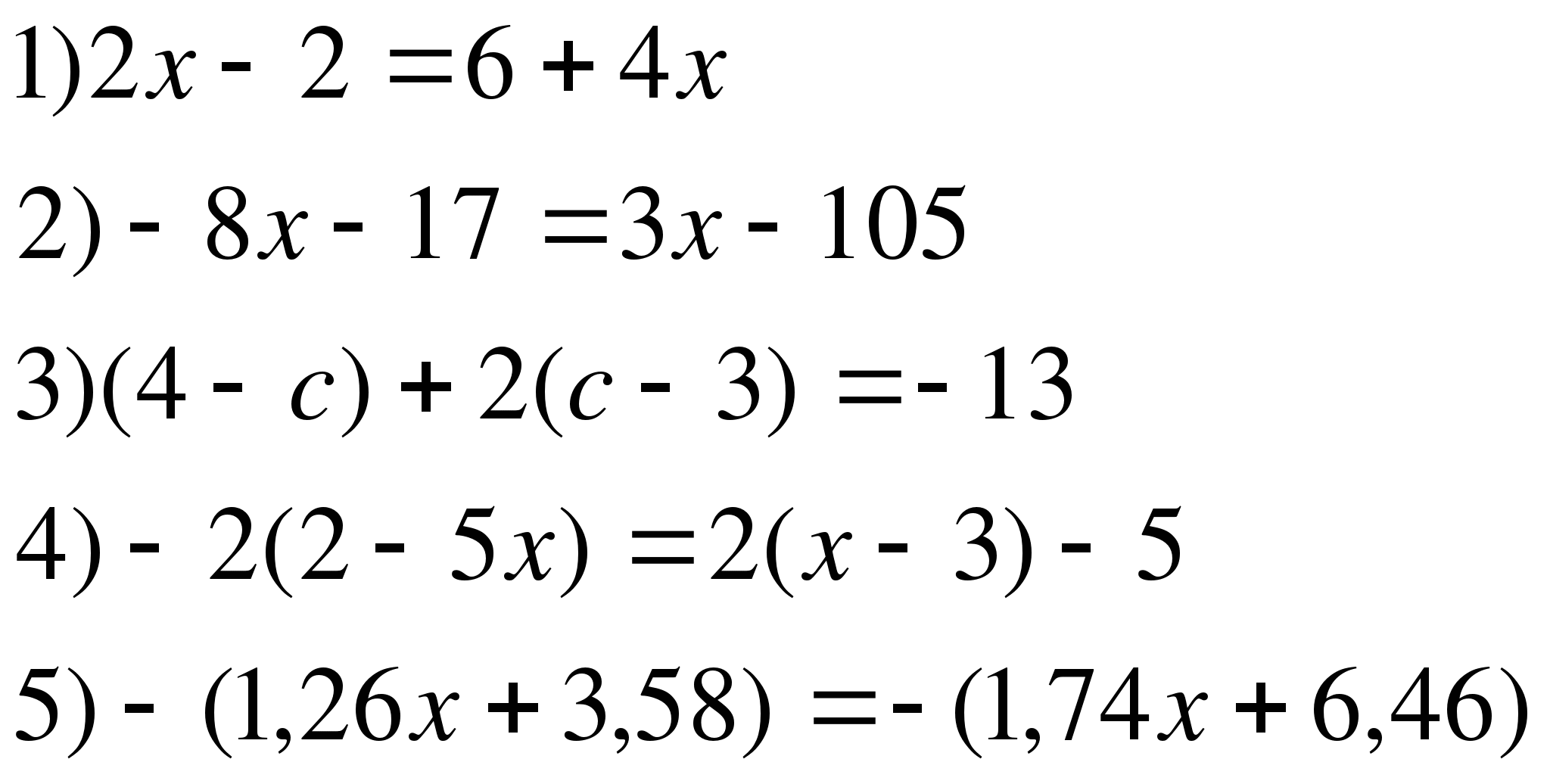
7.
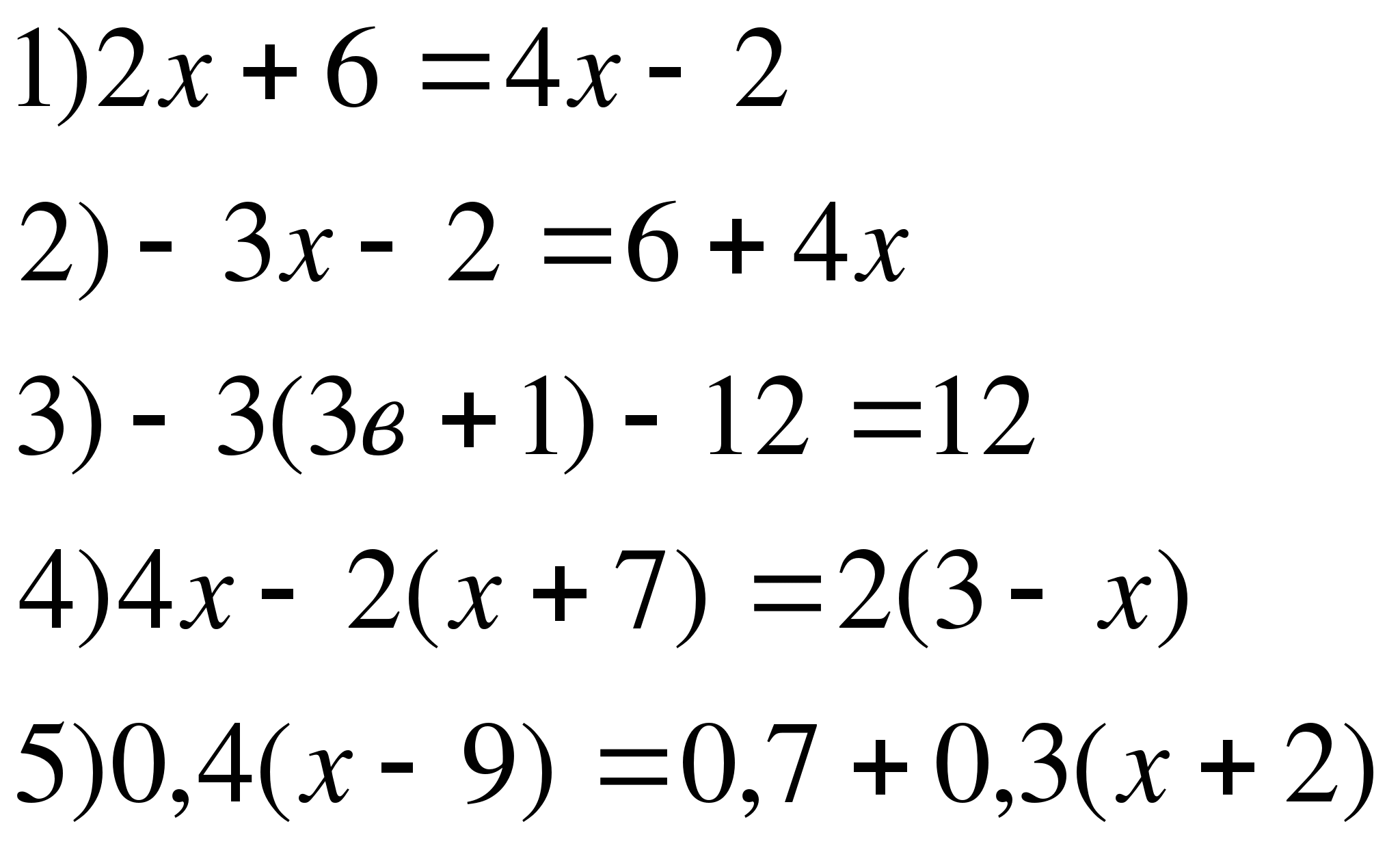
8.
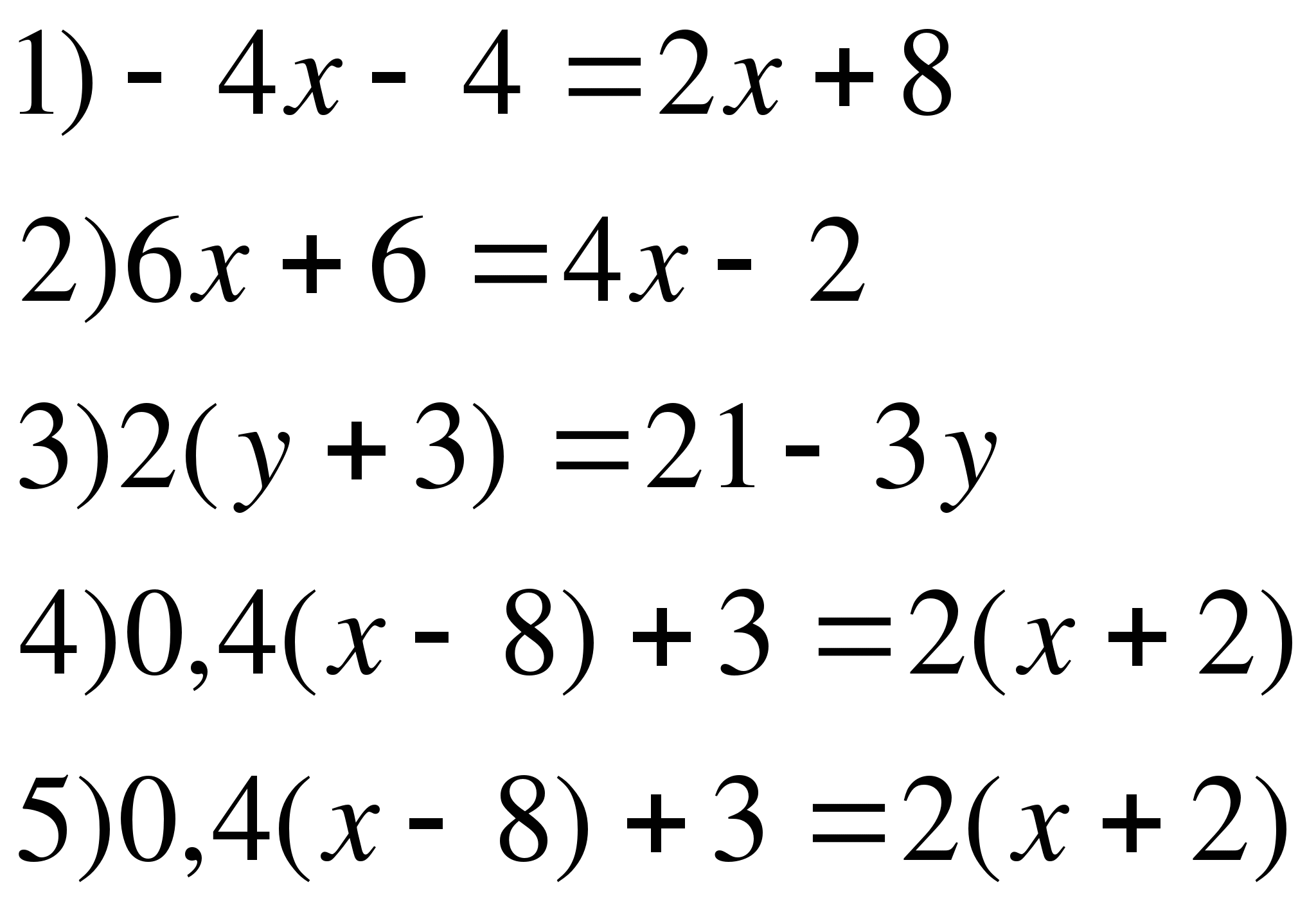
9.
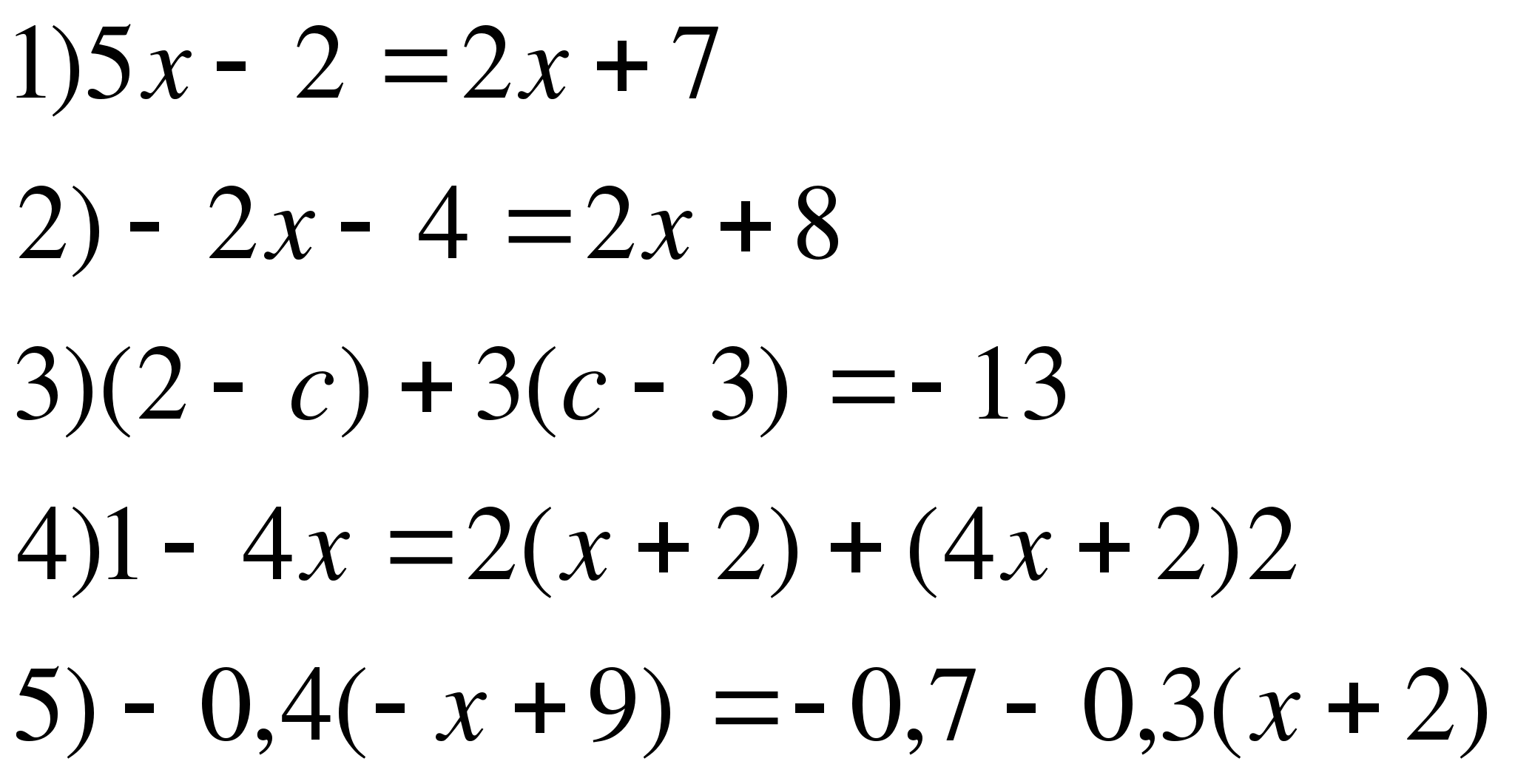
10.
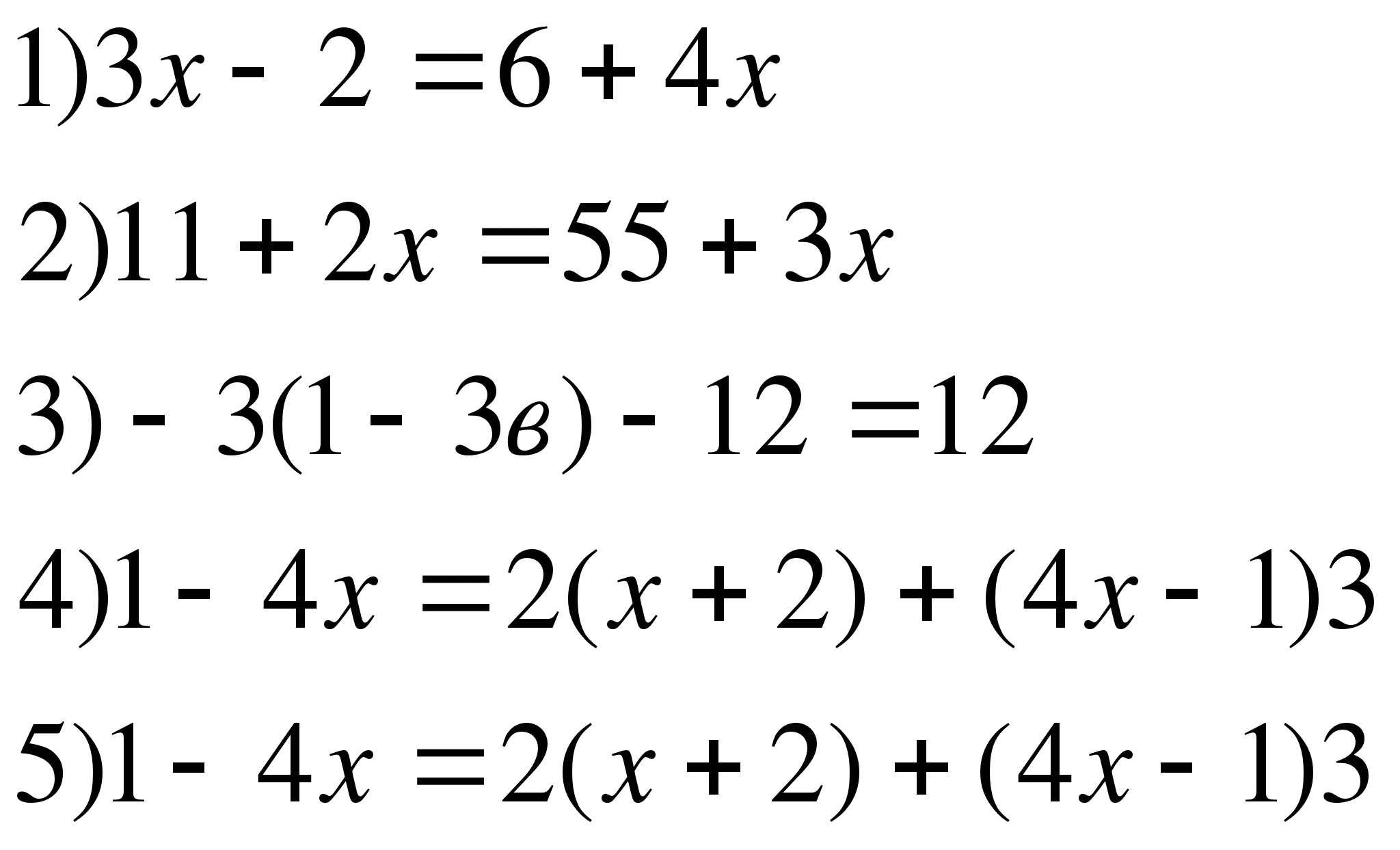
11.
1) 3х-5х= -13+3
2) 4х-7=2х+15
3) 7(2+у) – 3у=5у-6
4) 3(х-7)-(9-2х)=2(12-х)-(х-10)
5) 4(0,6х-0,3)-3(0,7х-0,1)=0
12.
1) -5у-17у=-50+6
2) 7х+12=10х-3
3) 4х-2(3+х)=9-х
4) 4(2-3х) – 2(9х-8)=15(1-х)+3(4-х)
5) 5(0,14-0,23х)+3(0,3х+0,1)=0
13.
1) -7х+12х=8-23
2) 33-5х=15-8х
3) 17+3(15-с)=(4-с)=(4-с)-2(с-5)
4) 7(3-х)-3(х-4)=5(3+2х)-2(-3-2х)
5) 0,6(х-1)-(х+1)=0
14.
1) 16х – 7х= -42 – 39
2) -24+3х=9х+18
3) -3(5а-1)+4а=2а+7(5-3а)
4) 4(х-16) – (8-х)=10(х+1)-2(15+8х)
5) 5(0,16х+0,33) – (3-х)=0
15.
1) у-12у=-6-27
2) -15х+31=-7+4х
3) 2(4-9а) – (2а+3)= -8(4-а)+3(1+2а)
4) (х+2)+х=9
5) 1,24х+3,46=1,76х+6,58
16.
1) -22у-18у=5*(-2)
2) 11-х=55+х
3) 5(2-3в)-4(6+2в)=28-(в-2)
4) 2(х-2)+3=0,4(х+8)
5) 5,96-1,8с=4,7-2,7с
17.
1) –х+6х= -45+15
2) 28-4х=19-х
3) -2(3х+4)+(6х+8)=4(5х-2)-(5х+8)
4) 2(5-3х)=6-5х
5) -4,92у-(0,08у+5,12)= — 0,88-у
18.
1) -27у-33у= — 12*(-5)
2) -35-2х=42+9х
3) 8(4-3у)-(7-2у)= -(6+3у)+8(у-2)
4) 11+2х=55+3х
5) -3(х-2)+4(1+2х)=10,3+20х
19.
1) х+(7+х)=11
2) (х+8)+(3-2х)=3
3) 10(у-2)=9(у-6)
4) 3(1-х)-5(х+2)=1-4х
5) -15-3х= — 7х+45
20.
1) х+2х-5=40
2) 3х-1-(х+2)=1
3) -5(5-3у)=16(у-3)
4) (2+х)2+(4х-1)3=10х-7
5) -4(1+2х)+3(х-2)= -18,3 – 20х
21.
1) х+(4+х)+х=16
2) (х-3)+(2х-4)= -1
3) 7(3у-5)= -10(3-2у)
4) (4+5х) – 3(2-х)=16х-0,4
5) 8(4-3у)-(7-2у)= -(6+3у)+8(у-2)
22.
1) 4х-3+(1-х)= -2
2) 14(3у-2)= -7(4-6у)
3) 2х+0,1 – 4(1-4х)=8х-4,4
4) 6х+6=4х-2
5) 2,44+2,3р=3,12+2,7р
23.
1) 3(х-2)=х+2
2) (х+2)+(4х-3)-(5-х)=1
3) 4х-3=2х+1
4) -2х-4=2х+8
5) 0,4(х-3)=0,5(4+х)-2,5
24.
1) 2(х-3)=7(2+х)
2) 3-(х+1)-(х-4)+(2х-1)=0
3) 2(1-х) – 4(2х+8)=8х+28
4) –(3у+7)=8-2(8-у)
5) 5,96-1,8с=4,7-2,7с
Урок математики по теме «Решение уравнений» для 6 класса — К уроку — Математика, алгебра, геометрия
Урок
по теме «Решение уравнений» в 6 классе
(Учебник:
Математика-6, И.И. Зубарева, А.Г. Мордкович)
Цели:
–
совершенствовать навык решения уравнений;
– ввести
понятия «переменная», «постоянная»;
– получить
алгоритм решения уравнений, содержащих
переменную в обеих частях равенства.
План
урока.
1.
Оргмомент
2.
Актуализация знаний
а)
Фронтальный опрос:
– сформулируйте
правило раскрытия
скобок;
– какие
слагаемые называются подобными?
– что
значит «привести
подобные»?
б)
Несколько учащихся работают по карточкам,
остальные выполняют тест по слайдам.
– Выберите
правильный ответ из предложенных, и
запишите соответствующую букву.
– Какое
слово вы получили? (Уравнение)
– У
кого получилось другое? (анализ ошибок)
3.
Постановка цели урока
Итак,
тема нашего урока «Решение уравнений»
(записывают в тетрадях).
– Что
называется уравнением? что значит решить
уравнение? что называется корнем
уравнения?
– Какой
алгоритм вы использовали при решении
уравнений?
– Есть
ли данных уравнений (Слайд 10), те которые
вы затрудняетесь решить?
– Чем
они отличаются от других? (неизвестная
величина в обеих частях равенства)
– Какова
же цель нашего урока? (научиться
решать уравнения, содержащие неизвестное
в обеих частях)
4.
Введение нового материала
Собрать
карточки.
– Какие
понятия вы получили? (переменная,
постоянная)
– Что
они означают?
Ввести
понятия «переменная» и «постоянная»
(Слайд 11).
– В
данных уравнениях (Слайд 12) назовите
слагаемые, содержащие переменную/слагаемые
без переменной.
Для
поиска алгоритма решения уравнений,
учащиеся делятся на группы.
Правила работы в группах:
каждый ряд решает 1 уравнение (Слайд 12)
в группе по 4 человека; группа сама
определяет, кто будет записывать решение,
а кто будет рассказывать решение у
доски; если группа не может найти решение,
то может воспользоваться вопросом-подсказкой;
оговаривается время работы (5-7 мин).
Решение записывают на маркерных досках
или бумаге (А3).
Вопросы-подсказки:
– когда
разность двух выражений равна нулю?
– чему
равна разность двух равных выражений?
– можно
ли к обеим частям равенства прибавить
одно и то же число?
Итог
работы в группах – получения алгоритма
решения уравнений, содержащих переменную
в обеих частях равенства (Слайд 13).
5.
Физкультминутка
6.
Закрепление
Работа
с учебником: № 580 (а, б), № 582 (а, б), доп. №
582 (г). Решение учащиеся записывают на
доске с проговариванием алгоритма.
7.
Первичная проверка знаний
Учащиеся
самостоятельно решают уравнения (Слайд
14). Сообщить время работы (7 мин). Для тех,
кто справится с решением быстрее
остальных, приготовить дополнительное
задание.
Самопроверка
(Слайды 15,16). Проговаривание алгоритма
решения.
– Поднимите
руку, кто решил все уравнения правильно.
Кто допустил одну ошибку? Кто не справился
с заданием?
8.
Подведение итогов урока
– Что
нового вы узнали сегодня на уроке? чему
научились?
Объявить
оценки за урок.
9.
Домашнее задание
§
19; № 579 – 581 (в, г), доп. № 592 (Слайд 17).