Напишите пожалуйста правила за 6 класс по математике
Делимость чисел
Делителем натурального числа «а» называют натуральное число , на которое «а» делится без остатка.
Кратным натурального числа «а» называют натуральное число , которое делится без остатка на «а» .
Любое натуральное число имеет бесконечно много кратных.
Признаки делимости на 10 , на 5 и на 2.
Если запись натурального числа оканчивается цифрой 0 , то это число делится без остатка на 10. Если запись натурального числа оканчивается другой цифрой , то оно не делится без остатка на 10.
Если запись натурального числа оканчивается цифрой 0 или 5 , то это число делится без остатка на 5. Если запись натурального числа оканчивается другой цифрой , то оно не делится без остатка на 5.
Если запись натурального числа оканчивается четной цифрой , то это число делится без остатка на 2. Если запись натурального числа оканчивается нечетной цифрой , то это число нечетно.
Признаки делимости на 3 на 9.
Если сумма цифр числа делится на 9 , то и число делится на 9 ; если сумма цифр числа не делится на 9 , то и число не делится на 9 ;
Если сумма цифр числа делится на 3 , то и число делится на 3 ; если сумма цифр числа не делится на 3 , то и число не делится на 3 ;
Простые и составные числа
Натуральное число называют простым , если оно имеет только два делителя : единицу и само это число.
Натуральное число называют составным , если оно имеет более двух делителей.
Число 1 имеет только один делитель : само это число .Поэтому его не относят ни к составным , ни кпростым.
Всякое составное число можно разложить на множители. При любом способе получается одно и то же разложение , если не учитывать порядка записи множителей.
Наибольший общий делитель . Взаимно простые числа.
Наибольшее натуральное число , на которое делятся без остатка числа а и б , называют наибольшим общим делителем этих чисел.
Натуральные числа называют взаимно простыми , если их наибольший общий делитель равен 1.
Чтобы найти НОД нескольких натуральных чисел, надо: 1) состав разложения одного из этих чисел, вычеркнуть те , которые не входят в разложение других чисел; 3) найти произведение оставшихся множителей.
Наименьшее общее кратное (НОК)
Наименьшим общим кратным натуральных чисел а и б называют наименьшее натуральное число, которое кратно и а и б.
Чтобы найти НОК нескольких натуральных чисел , надо: 1) разложить их на простые множители; 2) выписать множители , входящие в разложение одного из чисел; 3) добавить к ним недостающие множители из разложений остальных чисел; 4) найти произведение получившихся множителей.
Сложение и вычитание дробей с разными знаменателями.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число , то получится равная ей дробь.
Деление числителя и знаменателя на их обший делитель , отличный от единицы , называют сокращение дроби.
Наибольшее число , на которое можно сократить дробь , — это НОД ее числителя и знаменателя.
Дробь называется несократимой – если числитель и знаменатель являются взаимно простыми числами.
Чтобы привести дроби к наименьшему общему знаменателю , надо: 1) найти НОК знаменателей этих дробей, оно и будет их наименьшим общим знаменателем; 2) разделить НОЗ на знаменатели данных дробей , т.е. найти для каждой дроби дополнительный множитель; 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Чтобы сравнить ( сложить , вычесть) дроби с разными знаменателями , надо: 1) привести данные дроби к НОЗ; 2) сравнить ( сложить , вычесть ) полученные дроби.
Чтобы сложить смешанные числа , надо: 1) привести дробные части этих чисел к НОЗ; 2) отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части.
Чтобы выполнить вычитание смешанных чисел , надо: 1) привести дробные части этих чисел к НОЗ; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь , уменьшив на единицу целую часть;2) отдельно выполнить вычитание целых частей и отдельно дробных частей.
Умножение и деление обыкновенных дробей.
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число , а знаменатель оставить без изменения.
Чтобы умножить смешанное число на натуральное число , можно: 1) умножить целую часть на натуральное число; 2) умножить дробную часть на это натуральное число; 3) сложить полученные результаты.
Чтобы умножить дробь на дробь ,надо: 1) найти произведение числителей и произведение знаменателей этих дробей; 2) первое произведение записать числителем , а второе – знаменателем.
Для того чтобы выполнить умножение смешанных чисел , надо их записать в виде неправильных дробей , а затем воспользоваться правилом умножения дробей.
Нахождение дроби от числа.
Чтобы найти дробь от числа , нужно умножить число на эту дробь.
Нахождение числа по его дроби.
Чтобы найти число по данному значению его дроби , надо это значение разделить на дробь.
Взаимно обратные числа.
Два числа , произведение которых равно единице , называют взаимно обратными.
Деление.
1) Чтобы разделить одну дробь на другую , надо делимое умножить на число , обратное делителю.
Дробные выражения.
Частное двух чисел или выражений , в котором знак деления обозначен чертой , называют дробным выражением. Выражение , стоящее над чертой , называют числителем , а выражение стоящее под чертой – знаменателем дробного выражения.
Отношения и пропорции.
Частное двух чисел называют отношением этих чисел. Отношение показывает , во сколько раз первое число больше второго , или какую часть первое число составляет от второго.
Равенство двух отношений называют пропорцией.
В пропорции а/в=с/д числа а и д называют крайними членами пропорции , числа в и с –средними членами пропорции.
В верной пропорции произведение крайних членов равно произведению средних .
Если произведение крайних членов пропорции равно произведению средних членов пропорции , то пропорция верна. Это свойство называют основным свойством пропорции.
Две величины называют прямо пропорциональными , если при увеличении ( уменьшении ) одной из них в несколько раз другая увеличивается ( уменьшается ) во столько же раз.
Две величины называют обратно пропорциональными , если при увеличении ( уменьшении ) одной из них в несколько раз другая уменьшается ( увеличивается ) во столько же раз.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
Длина окружности и площадь круга.
Замкнутая линия все точки которой лежат на одинаковом расстоянии от одной точки «О»,называется окружностью.
Ту часть плоскости , которая лежит внутри окружности ( вместе с самой окружностью), называют кругом.
Точку «О» называют центром окружности и круга.
Отрезок соединяющий точку окружности с центром называют радиусом. Все радиусы одной окружности равны.
Отрезок соединяющий две точки окружности и проходящий через центр окружности называется диаметром. Диаметр состоит из двух радиусов , поэтому диаметр окружности в 2 раза длиннее ее радиуса.
Диаметр делит круг на 2 полукруга , а окружность – на 2 полуокружности.
Часть окружности между двумя точками называют дугой окружности.
Длина окружности прямо пропорциональна длине её диаметра. Поэтому для всех окружностей отношение длины окружности к длине её диаметра является одним и тем же числом. Его обозначают греческой буквой П- пи . Формула длины окружности: С=п d или C=2пr. П= 3,1416…..
Все точки поверхности шара одинаково удалены от центра шара.
Отрезок, соединяющий точку поверхности шара с центром ,называют радиусом шара.
Отрезок , соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара.
Диаметр шара равен двум радиусам.
Поверхность шара называют сферой.
Рациональные числа.
Положительные и отрицательные числа.
Числа со знаком + называют положительными.
Числа со знаком – называют отрицательными.
Прямую с выбранными на ней началом отсчета , единичным отрезком и направлением называют координатной прямой.
Число, показывающее положение точки на прямой , называют координатой этой точки.
Два числа , отличающиеся друг от друга только знаками, называют противоположными числами.
Натуральные числа , противоположные числа и нуль называют целыми числами.
Модулем числа а называют расстояние ( в единичных отрезках) от начала координат до точки А(а).
Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу.
Противоположные числа имеют равные модули.
Сравнение чисел.
Любое отрицательное число меньше любого положительного числа.
Из двух отрицательных чисел меньше то, модуль которого больше.
Нуль больше любого отрицательного числа , но меньше любого положительного числа.
На горизонтальной координатной прямой точка с большей координатой лежит правее точки с меньшей координатой.
Сложение и вычитание положительных и отрицательных чисел.
Любое число от прибавления положительного числа увеличивается , а от прибавления отрицательного числа уменьшается.
Сумма двух противоположных чисел равна нулю.
Чтобы сложить два отрицательных числа , надо: а)сложить их модули; б) поставить перед полученным числом знак — .
Чтобы сложить два числа с разными знаками, надо: а) из большего модуля слагаемых вычесть меньший; б) поставить перед полученным числом знак того слагаемого , модуль которого больше.
Чтобы из данного вычесть другое ,надо к уменьшаемому прибавить число , противоположное вычитаемому: а-б=а+(-б)
Любое выражение содержащее лишь знаки сложения и вычитания , можно рассматривать как сумму.
Чтобы найти длину отрезка на координатной прямой ,надо из координаты его правого конца вычесть координату его левого конца.
Умножение и деление положительных и отрицательных чисел.
Чтобы перемножить два числа с разными знаками , надо перемножить модули этих чисел и поставить перед полученным числом знак — .
Чтобы перемножить два отрицательных числа , надо перемножить их модули.
Чтобы разделить отрицательное число на отрицательное , надо разделить модуль делимого на модуль делителя.
При делении чисел с разными знаками , надо: а) разделить модуль делимого на модуль делителя; б) поставить перед полученным числом знак — .
Рациональные числа.
Число , которое можно записать в виде отношения а/н , где а-целое число , а н-натуральное число , называют рациональным числом.
Любое целое число является рациональным.
Сумма , разность и произведение рациональных чисел тоже рациональные числа.
Если делитель отличен от нуля , то частное двух рациональных чисел тоже рациональное число.
Любое рациональное число можно записать либо в сиде десятичной дроби ( в частности целого числа ) , либо в виде периодической дроби.
Сложение рациональных чисел обладает переместительным и сочетательным свойствами.
Умножение рациональных чисел тоже обладает переместительным и сочетательным свойствами.
Произведение может быть равно нулю лишь в том случае , когда хотя бы один из множителей равен нулю.
Умножение рациональных чисел обладает распределительным свойством относительно сложения.
Решение уравнений.
Если перед скобками стоит знак + , то можно опустить скобки и этот знак + , сохранив знаки слагаемых , стоящих в скобках.Если первое слагаемое записано без знака , то его надо записать со знаком + .
Чтобы раскрыть скобки перед которыми стоит знак — , надо заменить этот знак на + , поменяв знаки всех слагаемых в скобках на противоположные , а потом раскрыть скобки.
Подобные слагаемые.
Если выражение является произведением числа и одной или нескольких букв , то это число называют числовым коэффициентом ( или просто коэффициентом ).
Слагаемые , имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Чтобы сложить ( или говорят : привести ) подобные слагаемые , надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Решение уравнений.
Корни уравнения не изменяются , если обе части уравнения умножить или разделить на одно и то же число , не равное нулю.
Корни уравнения не изменяются , если какое –нибудь слагаемое перенести из одной части уравнения в другую , изменив при этом его знак.
Уравнение , которое можно привести к виду ах=в с помощью переноса слагаемых и приведения подобных , называют линейным уравнением с одним неизвестным.
Координаты на плоскости.
Две прямые , образующие при пересечении прямые углы , называют перпендикулярными.
Отрезки ( или лучи) , лежащие на перпендикулярных прямых , называют перпендикулярными отрезками ( или лучами).
Две непересекающиеся прямые на плоскости называют параллельными.
Если две прямые в плоскости перпендикулярны третьей , то они параллельны.
Через каждую точку плоскости , не лежащую на данной прямой , можно провести только одну прямую , параллельную данной прямой.
Отрезки ( или лучи) , лежащие на параллельных прямых , называют параллельными отрезками ( или лучами).
Системой координат на плоскости называют две перпендикулярные координатные прямые- х и у , которые пересекаются в начале отсчета – точке О. Тока О называется началом координат.
Плоскость на которой выбрана система координат , называют координатной плоскостью.
Координатную прямую х называют осью абсцисс , а у – осью ординат.
Онлайн уроки по математике за 6 класс

Какое число называется делителем (кратным) данного числа? Какое число является делителем любого натурального числа? Чему равен самый маленький (большой) делитель числа а? Чему равно самое маленькое кратное числа а?


Как по записи числа определить, делится ли оно на 2; 5; 10 без остатка? Что такое четное (нечетное) число?


Как по записи числа определить, делится ли оно на 3; 9? Как по записи числа определить, делится ли оно на 6; 18; 15?


На этом уроке мы познакомимся с вами с двумя видами чисел, которые различаются количеством делителей.


Существует ли составное число, которое нельзя разложить на простые множители? Чем могут отличаться два разложения одного и того же числа на простые множители?


Какое число называется наибольшим общим делителем (НОД) двух натуральных чисел? Всегда ли он существует? Какие числа называются взаимно простыми? Как найти НОД двух (трех) натуральных чисел?


Какое число называется наименьшим общим кратным (НОК) чисел а и b? Всегда ли оно существует? Как найти НОК двух (трех) чисел?


В чем состоит основное свойство дроби?


Что значит сократить дробь? Какая дробь называется несократимой?


Какое число может служить общим знаменателем двух дробей? Какое число называется дополнительным множителем?


Какие правила сравнения дробей мы изучили? Как сравнить две дроби с разными знаменателями?


Как сложить (вычесть) дроби с разными знаменателями? Как сложить (вычесть) обыкновенную и десятичную дроби?


Как сложить два смешанных числа? Как выполнить вычитание смешанных чисел? Как сложить (вычесть) десятичную дробь и смешанное число?


Как умножить дробь на натуральное число? Как умножить дробь на дробь? В чем состоит алгоритм умножения смешанных чисел?


Как найти дробь от числа? Как найти несколько процентов от числа? Как применяется нахождение дроби от числа для решения задач?


Как умножить смешанное число на натуральное? Как применяется распределительное свойство умножения для рационализации вычислений с обыкновенными дробями и смешанными числами?


Какие числа называются взаимно обратными? Какое число является обратным самому себе?


Как разделить дробь на натуральное число? Как разделить дробь на дробь? Как выполняется деление смешанных чисел?


Как найти число по заданному значению его дроби? Как найти число по заданному значению его процентов?


Какое выражение называется дробным? Что называется числителем, знаменателем дробного выражения? Как найти значение дробного выражения?


Что называется отношением двух чисел? Что показывает отношение двух чисел? Как найти, какую часть число а составляет от числа b?


Что называется пропорцией? Какие члены пропорции называются средними, а какие крайними? Как составить верную пропорцию?


Какие величины называются прямо пропорциональными (обратно пропорциональными)? Что можно сказать об отношениях соответствующих значений прямо пропорциональных (обратно пропорциональных) величин?


Что называется масштабом карты, плана, чертежа? Какие виды масштабов бывают? Как применяется понятие «масштаб» для решения задач?


Что называется окружностью, радиусом, диаметром окружности? Как найти длину окружности, зная ее радиус? Как найти площадь круга, зная радиус ограничивающей его окружности?


Что называется радиусом шара, его диаметром? Что называется сферой?


Какие числа называются положительными, отрицательными? Является ли нуль положительным, отрицательным числом? Какая прямая называется координатной прямой?


Какие числа называются противоположными? Какое число противоположно самому себе? Сколько противоположных чисел есть у каждого числа?


Что называется модулем числа? Как обозначается модуль числа? Чему равен модуль положительного (отрицательного) числа, нуля?


Как сравнить два числа с разными (одинаковыми) знаками? Какие правила сравнения чисел с нулем вы знаете? Как сравнить число и его модуль?


Что означает положительное (отрицательное) перемещение точки на координатной прямой? Где в реальной жизни мы сталкиваемся с изменениями величин?


Что значит прибавить к числу а число b? Как изменится число а, если b положительное (отрицательное) число?


Как сложить два отрицательных числа? Может ли при сложении двух отрицательных чисел получиться нуль, положительное число?


Как сложить два числа с разными знаками? Может ли сумма двух чисел с разными знаками быть положительным (отрицательным) числом, нулем?


Что означает вычесть из числа а число d? Может ли разность двух чисел быть числом положительным, нулем, отрицательным?


Как перемножить два числа с разными знаками? Как перемножить два отрицательных числа? Как возвести в квадрат положительное, отрицательное число? Какое число получается в результате?


Как разделить отрицательное число на отрицательное? Как разделить числа с разными знаками?


Какие числа называются рациональными? Существуют ли числа, не являющиеся рациональными?


Какими свойствами обладает сложение (умножение) рациональных чисел? Как применяются свойства действий с рациональными числами для упрощения выражений, нахождения значения выражений?


Как раскрыть скобки, перед которыми стоит знак «+», «—»? Как записать сумму (разность) двух выражений и упростить ее?


Что называется коэффициентом выражения? Как определить знак коэффициента в выражении?


Какие слагаемые называются подобными? Чем могут отличаться подобные слагаемые? Что значит привести подобные слагаемые?


Изменятся ли корни уравнения, если обе части уравнения умножить на ненулевое число? На нуль? Как перенести слагаемое из одной части уравнения в другую?


Какие прямые называются перпендикулярными? Какие отрезки, лучи называются перпендикулярными? Как построить перпендикулярные прямые?


Как расположены на плоскости две прямые, перпендикулярные третьей прямой?


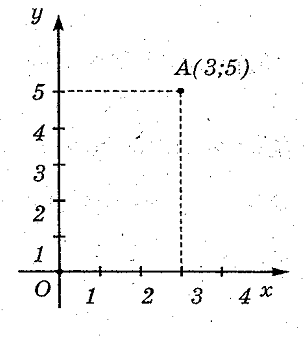
Как называют пару чисел, определяющих положение точки на координатной плоскости? Как называется первая (вторая) координата точки? Как построить точку с заданными координатами в прямоугольной системе координат?


В чем отличие столбчатой диаграммы от круговой? Как построить столбчатую диаграмму по данным задачи?


Как по графику зависимости величин определять соответствующие значения этих величин? Как построить график зависимости величин по данным задачи?


Условия Пакетного предложения можно узнать, раскрыв этот блок

Лэйдл предлагает пройти онлайн-уроки по математике за 6 класс. Все занятия проходят в режиме онлайн и позволяют значительно повысить знания ребенка по данной дисциплине, разобраться с нюансами школьной программы и улучшить оценки по предмету.
В 6 классе у многих школьников возникают сложности с дробями и операциями деления – именно эти темы являются основными. При помощи грамотно структурированных уроков ребенок научится выполнять простейшие подсчеты без многочасового изучения материала. Лэйдл делает упор на логику и интуитивное понимание математики.
3 причины изучать математику вместе с Лэйдл
- Структурированная программа.
Над разработкой уроков работали профессиональные преподаватели, которые смогли выделить самую важную информацию о дробях и представить ее в четко структурированной форме. Это значительно облегчило процесс обучения и сделало его максимально простым и понятным. - Мультимедиа.
Чтобы упростить восприятие теории, мы снабдили каждый урок мультимедийными материалами. - Практика.
Кроме теоретической основы, Лэйдл дает множество практических примеров и заданий. Решая задачи и уравнения онлайн, ребенок учится применять полученные знания в реальной жизни.
Чтобы дроби больше не пугали вашего ребенка, зарегистрируйтесь на Лэйдл и пройдите пробный урок по математике бесплатно!
Конспект «Математика 6 класс. Краткий курс»
«Математика 6 класс. Краткий курс» — это сжатое, но полное изложение школьного курса по математике в 6 классе по учебным программам Белоруссии, представленное в виде логических схем и информационных таблиц. Наглядное, четкое и схематичное изложение материала позволяет быстро усвоить или повторить большой объем информации, облегчить понимание трудных тем, сложных понятий и определений, обобщить и систематизировать знания. Содержание данного курса соответствует учебному пособию «Герасимов, В.Д., Пирютко, О.Н. Математика / Матэматыка 6 класс. Адукацыя і выхаванне, 2018». Обращаем Ваше внимание на различие учебных программ России и Белоруссии! Содержание учебного предмета «Математика 6 класс в Белоруссии» указано в конце настоящей статьи (см. внизу).
Глава 1. ДЕСЯТИЧНЫЕ ДРОБИ
1.1. Числа и величины

1.2. Десятичная дробь
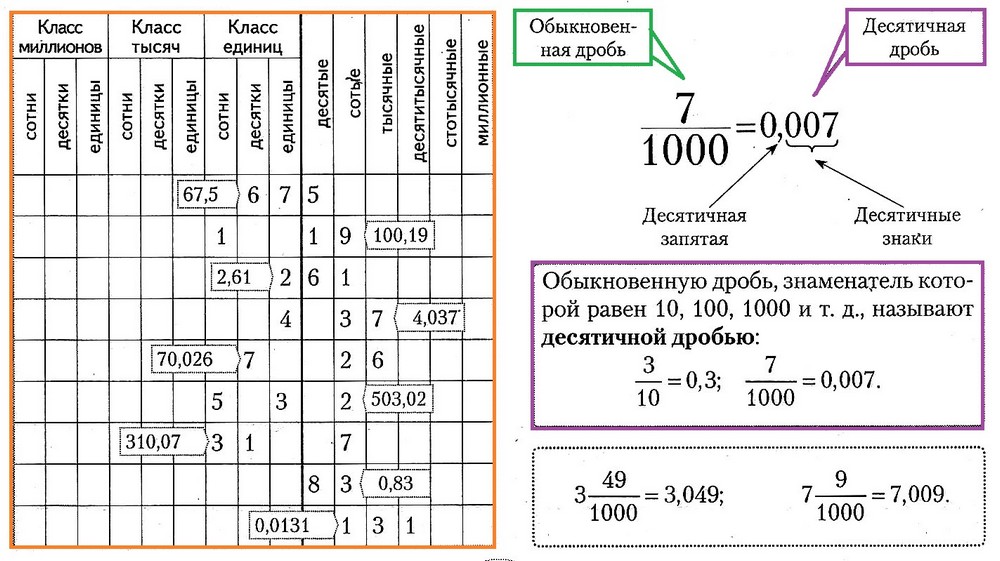
1.3. Сравнение десятичных дробей

1.4. Округление десятичных дробей

1.5. Сложение и вычитание десятичных дробей

1.6. Умножение и деление десятичных дробей на разрядную единицу

1.7. Умножение десятичных дробей

1.8. Деление десятичных дробей

1.9. Преобразование десятичных дробей в обыкновенные
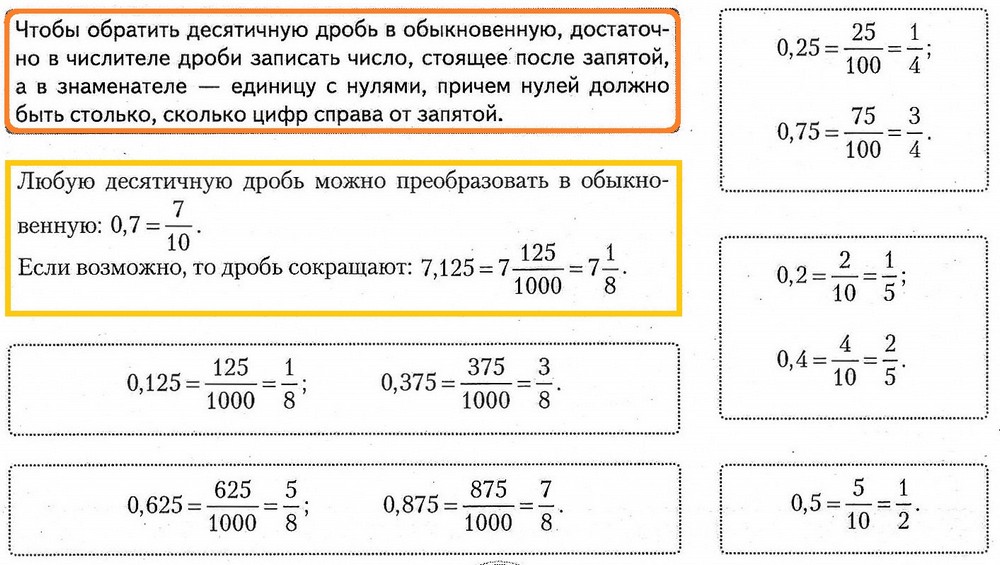
1.10. Преобразование обыкновенных дробей в десятичные
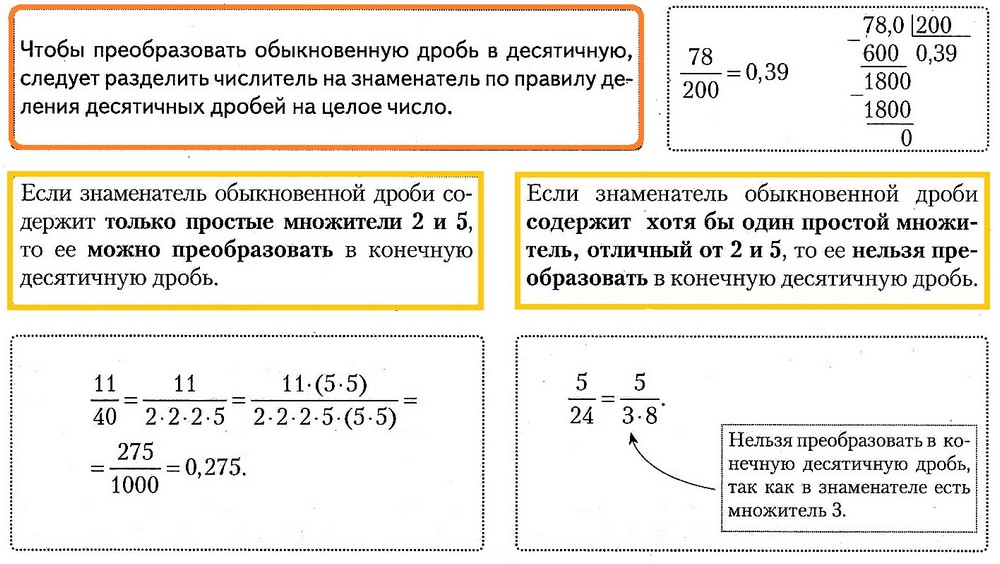
Глава 2. ПРОЦЕНТЫ И ПРОПОРЦИИ
2.1. Отношения чисел и величин

2.2. Проценты

2.3. Ключевые задачи на проценты
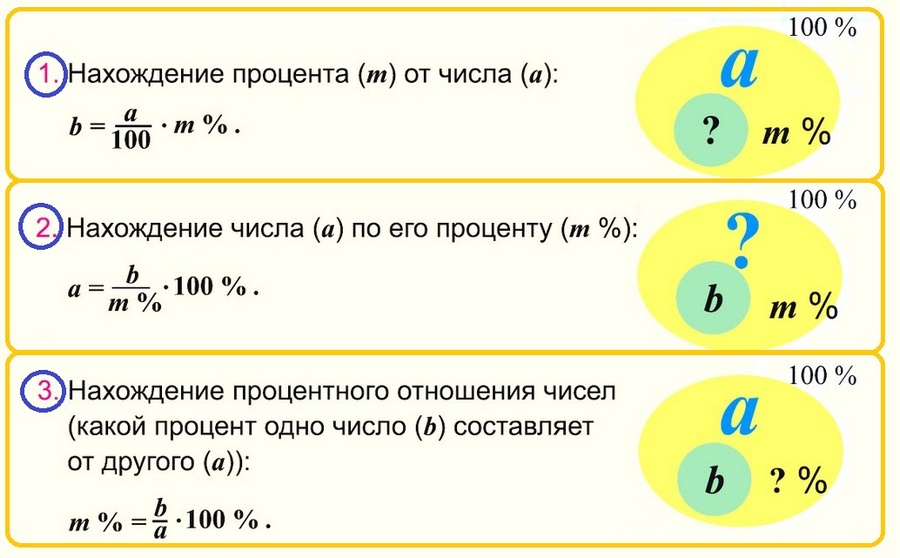
2.4. Алгоритм определения типа задачи на проценты

2.5. Пропорция и ее свойства

2.6. Вычисление неизвестных членов пропорции

2.7. Прямая пропорциональная зависимость
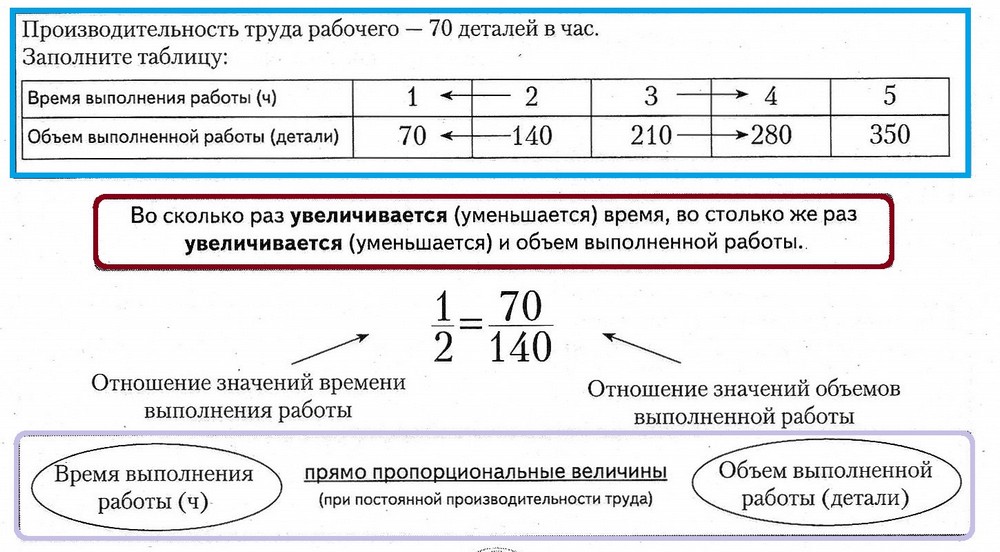
2.8. Обратная пропорциональная зависимость
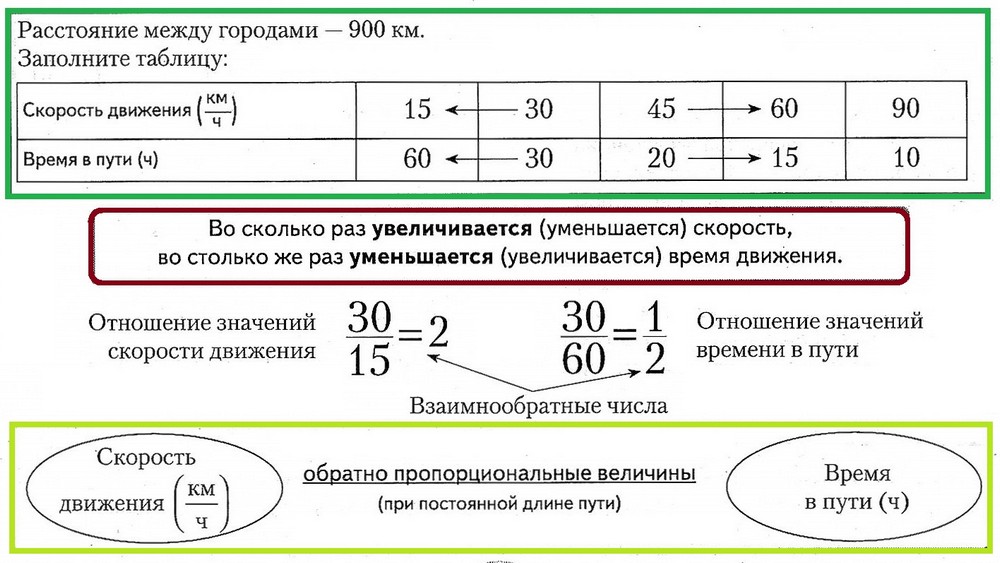
2.9. Круговые диаграммы

2.10. Масштаб

Подробнее про масштаб в Конспекте урока по Географии «Масштаб. Определение расстояний»
Глава 3. МНОЖЕСТВО
3.1 Множество и его элементы

3.2. Способы задания множеств

3.3. Подмножество

3.4. Пересечение множеств

3.5. Разность множеств

3.6. Объединение множеств

3.7. Законы операций над множествами

Глава 4. РАЦИОНАЛЬНЫЕ ЧИСЛА
4.1. Рациональные числа
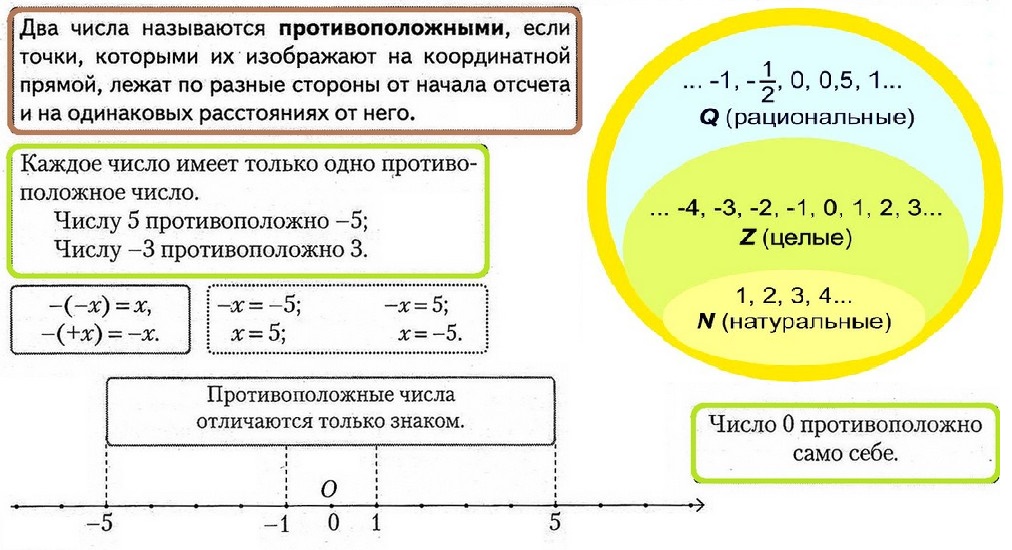
4.2 Координатная прямая
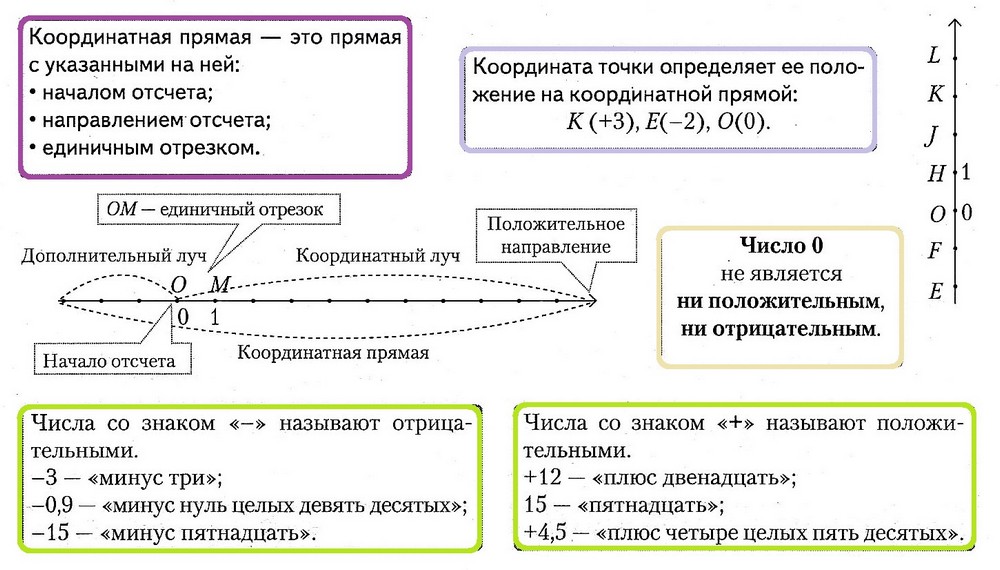
4.3 Модуль числа и его геометрический смысл

4.4. Сравнение рациональных чисел

4.5. Сложение рациональных чисел

4.6. Вычитание рациональных чисел

4.7. Умножение рациональных чисел
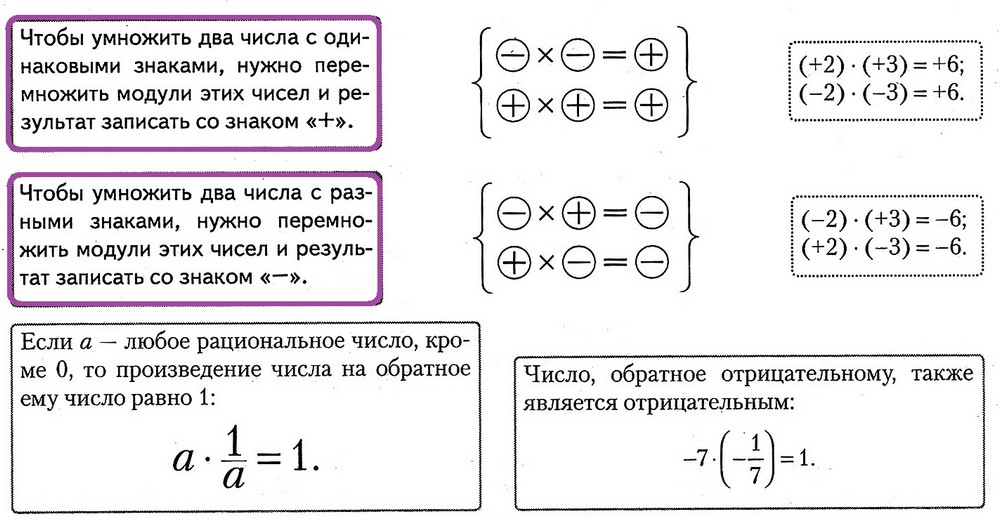
4.8. Деление рациональных чисел

Глава 5. КООРДИНАТНАЯ ПЛОСКОСТЬ
5.1. Длина окружности

5.2. Площадь круга

5.3. Биссектриса угла
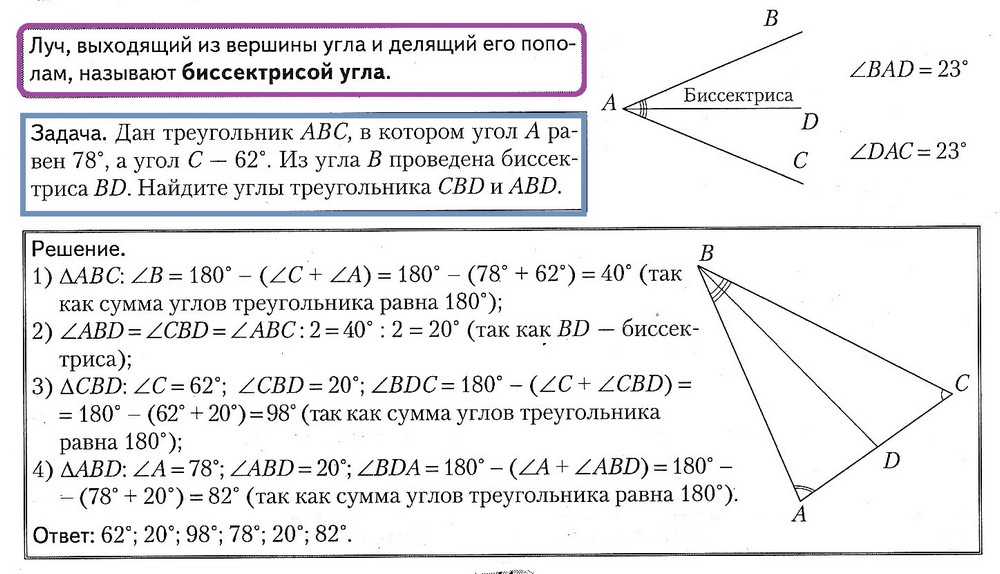
5.4. Виды треугольников
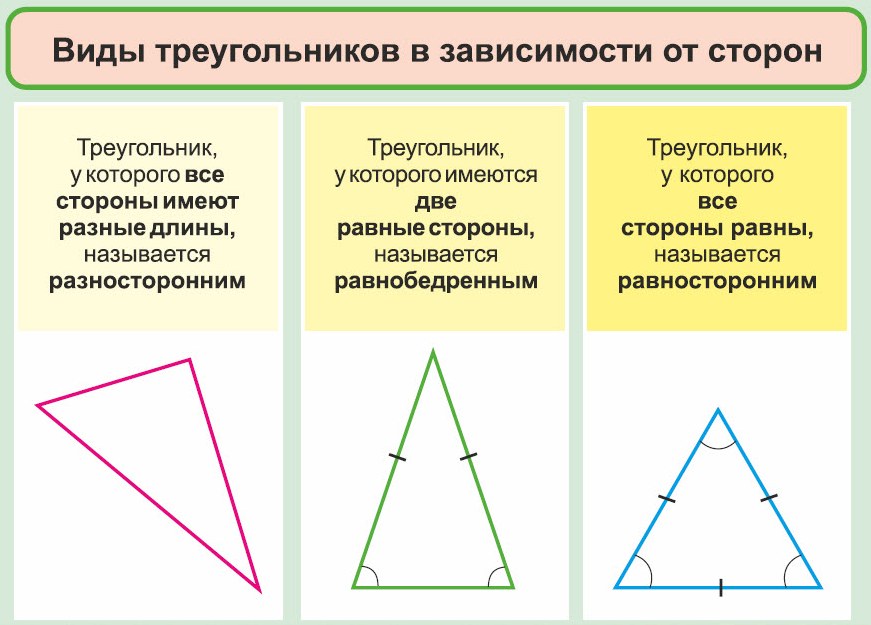

5.5. Свойство углов равнобедренного треугольника
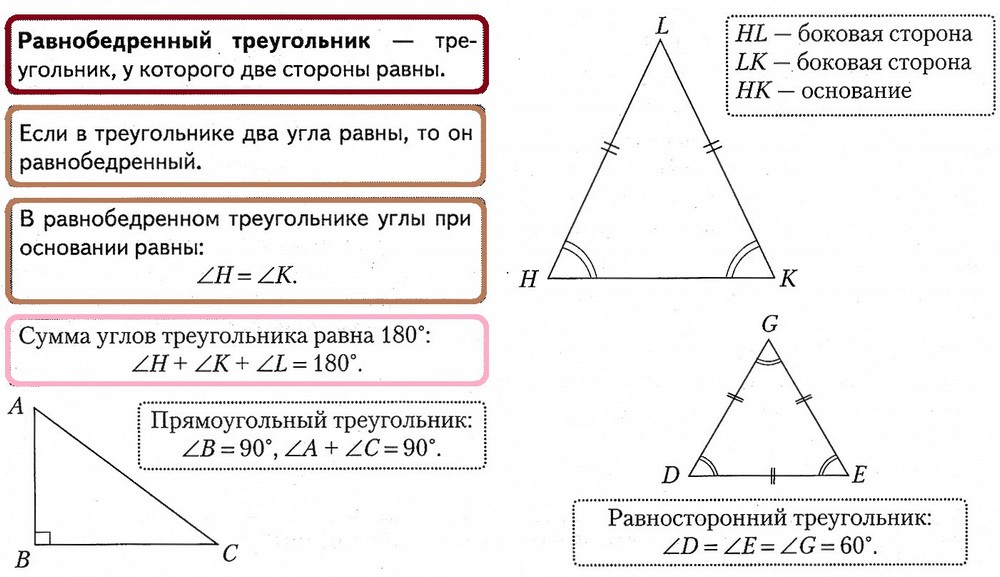
5.6. Симметрия относительно точки
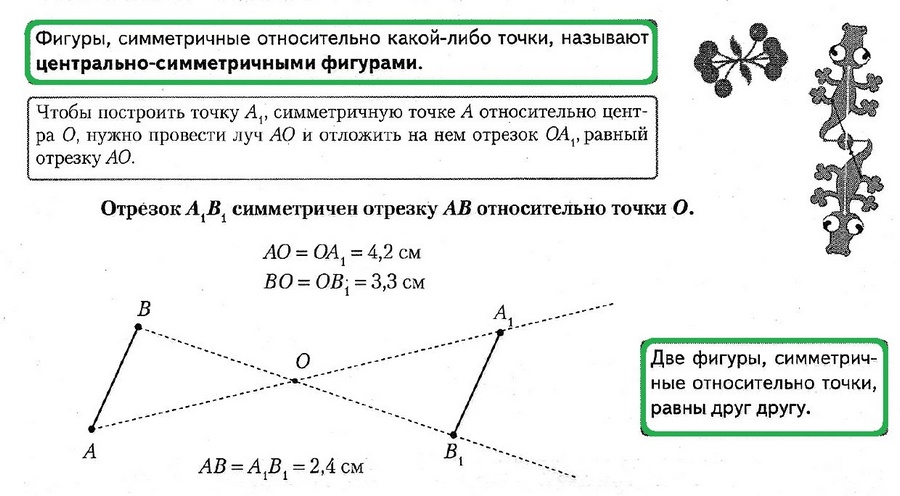
5.7. Симметрия относительно прямой
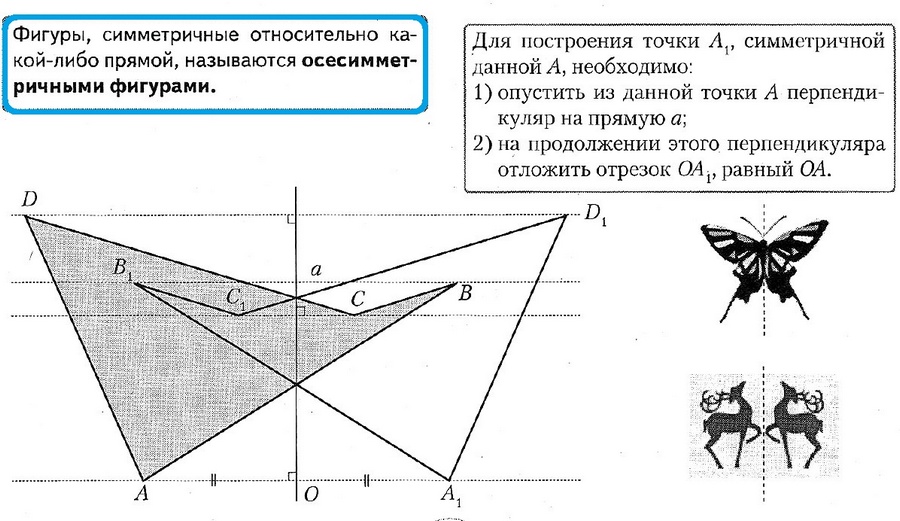
Содержание учебного предмета «Математика 6 класс в Белоруссии»
Десятичные дроби
Десятичные дроби. Сравнение десятичных дробей. Округление десятичных дробей. Конечная и бесконечная десятичные дроби. Сложение, вычитание, умножение и деление десятичных дробей. Умножение и деление десятичной дроби на разрядную единицу. Преобразования числовых выражений с обыкновенными и десятичными дробями.
Проценты и пропорции
Проценты. Основные задачи на проценты. Пропорция и ее свойства. Прямая пропорциональная зависимость. Обратная пропорциональная зависимость. Зависимости между величинами в процессах: скоростью, временем, результатом процесса; стоимостью, ценой, количеством и т.д. Задачи на применение пропорций (задачи на части, пропорциональное деление) и их решение. *Сложные проценты. Круговые диаграммы. Масштаб. Практико-ориентированные задачи, задачи с межпредметным содержанием и их решение.
Множество
Множество. Элементы множества. Способы задания множеств. Пустое множество. Подмножество. Операции над множествами (пересечение, объединение). Задачи на нахождение общих элементов и всех элементов заданных множеств. * Разность, дополнение множеств. * Круги Эйлера. Решение задач с помощью кругов Эйлера.
Рациональные числа
Множество натуральных чисел. Множество целых чисел. Множество рациональных чисел. Модуль числа. Сравнение рациональных чисел. Координатная прямая. Координаты точек на координатной прямой. Изображение точки на координатной прямой по ее координате. Нахождение координаты точки на координатной прямой. Геометрическая интерпретация модуля числа. Действия над рациональными числами. * Нахождение значений выражений, содержащих знак модуля. Практико-ориентированные задачи, задачи с межпредметным содержанием и их решение.
Координатная плоскость
Прямоугольная (декартова) система координат на плоскости. Координаты точки. Построение точки по ее координатам. Определение координат точки на координатной плоскости. Графики зависимостей между величинами. Графики реальных процессов: изменение суточной температуры воздуха, изменение пути в зависимости от скорости и времени движения, иных процессов. График прямой пропорциональности. График обратной пропорциональности. Практико-ориентированные задачи, задачи с межпредметным содержанием и их решение.
Наглядная геометрия
Наглядные представления тел в пространстве, примеры разверток. Окружность (центр, радиус, хорда, диаметр. Круг. Формулы длины окружности и площади круга. * Круг и его части (сегмент, сектор, кольцо). Виды треугольников (произвольный треугольник, равнобедренный треугольник, равносторонний треугольник, остроугольный треугольник, прямоугольный треугольник, тупоугольный треугольник).
Симметрия относительно точки. Фигуры, симметричные относительно точки. Центрально-симметричные фигуры. Центр симметрии. Фигуры в реальной жизни, имеющие центр симметрии. Фигуры, симметричные относительно прямой. Ось симметрии. Фигуры в реальной жизни, имеющие ось симметрии. Практико-ориентированные задачи, задачи с межпредметным содержанием и их решение.
* Познавательные и развивающие задачи с геометрическими фигурами.
Конец конспекта «Математика 6 класс. Краткий курс». Выберите следующие действия:
Вернуться к Списку конспектов
. Проверить знания по Математике
Определения и формулы математика 6 класс.
Делимость чисел
Делителем натурального числа «а» называют натуральное число , на которое «а» делится без остатка.
Кратным натурального числа «а» называют натуральное число , которое делится без остатка на «а» .
Любое натуральное число имеет бесконечно много кратных.
Признаки делимости на 10 , на 5 и на 2.
Если запись натурального числа оканчивается цифрой 0 , то это число делится без остатка на 10. Если запись натурального числа оканчивается другой цифрой , то оно не делится без остатка на 10.
Если запись натурального числа оканчивается цифрой 0 или 5 , то это число делится без остатка на 5. Если запись натурального числа оканчивается другой цифрой , то оно не делится без остатка на 5.
Если запись натурального числа оканчивается четной цифрой , то это число делится без остатка на 2. Если запись натурального числа оканчивается нечетной цифрой , то это число нечетно.
Признаки делимости на 3 на 9.
Если сумма цифр числа делится на 9 , то и число делится на 9 ; если сумма цифр числа не делится на 9 , то и число не делится на 9 ;
Если сумма цифр числа делится на 3 , то и число делится на 3 ; если сумма цифр числа не делится на 3 , то и число не делится на 3 ;
Простые и составные числа
Натуральное число называют простым , если оно имеет только два делителя : единицу и само это число.
Натуральное число называют составным , если оно имеет более двух делителей.
Число 1 имеет только один делитель : само это число .Поэтому его не относят ни к составным , ни кпростым.
Всякое составное число можно разложить на множители. При любом способе получается одно и то же разложение , если не учитывать порядка записи множителей.
Наибольший общий делитель . Взаимно простые числа.
Наибольшее натуральное число , на которое делятся без остатка числа а и б , называют наибольшим общим делителем этих чисел.
Натуральные числа называют взаимно простыми , если их наибольший общий делитель равен 1.
Чтобы найти НОД нескольких натуральных чисел, надо: 1) состав разложения одного из этих чисел, вычеркнуть те , которые не входят в разложение других чисел; 3) найти произведение оставшихся множителей.
Наименьшее общее кратное (НОК)
Наименьшим общим кратным натуральных чисел а и б называют наименьшее натуральное число, которое кратно и а и б.
Чтобы найти НОК нескольких натуральных чисел , надо: 1) разложить их на простые множители; 2) выписать множители , входящие в разложение одного из чисел; 3) добавить к ним недостающие множители из разложений остальных чисел; 4) найти произведение получившихся множителей.
Сложение и вычитание дробей с разными знаменателями.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число , то получится равная ей дробь.
Деление числителя и знаменателя на их обший делитель , отличный от единицы , называют сокращение дроби.
Наибольшее число , на которое можно сократить дробь , — это НОД ее числителя и знаменателя.
Дробь называется несократимой – если числитель и знаменатель являются взаимно простыми числами.
Чтобы привести дроби к наименьшему общему знаменателю , надо: 1) найти НОК знаменателей этих дробей, оно и будет их наименьшим общим знаменателем; 2) разделить НОЗ на знаменатели данных дробей , т.е. найти для каждой дроби дополнительный множитель; 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Чтобы сравнить ( сложить , вычесть) дроби с разными знаменателями , надо: 1) привести данные дроби к НОЗ; 2) сравнить ( сложить , вычесть ) полученные дроби.
Чтобы сложить смешанные числа , надо: 1) привести дробные части этих чисел к НОЗ; 2) отдельно выполнить сложение целых частей и отдельно дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части.
Чтобы выполнить вычитание смешанных чисел , надо: 1) привести дробные части этих чисел к НОЗ; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь , уменьшив на единицу целую часть;2) отдельно выполнить вычитание целых частей и отдельно дробных частей.
Умножение и деление обыкновенных дробей.
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число , а знаменатель оставить без изменения.
Чтобы умножить смешанное число на натуральное число , можно: 1) умножить целую часть на натуральное число; 2) умножить дробную часть на это натуральное число; 3) сложить полученные результаты.
Чтобы умножить дробь на дробь ,надо: 1) найти произведение числителей и произведение знаменателей этих дробей; 2) первое произведение записать числителем , а второе – знаменателем.
Для того чтобы выполнить умножение смешанных чисел , надо их записать в виде неправильных дробей , а затем воспользоваться правилом умножения дробей.
Нахождение дроби от числа.
Чтобы найти дробь от числа , нужно умножить число на эту дробь.
Нахождение числа по его дроби.
Чтобы найти число по данному значению его дроби , надо это значение разделить на дробь.
Взаимно обратные числа.
Два числа , произведение которых равно единице , называют взаимно обратными.
Деление.
1) Чтобы разделить одну дробь на другую , надо делимое умножить на число , обратное делителю.
Дробные выражения.
Частное двух чисел или выражений , в котором знак деления обозначен чертой , называют дробным выражением. Выражение , стоящее над чертой , называют числителем , а выражение стоящее под чертой – знаменателем дробного выражения.
Отношения и пропорции.
Частное двух чисел называют отношением этих чисел. Отношение показывает , во сколько раз первое число больше второго , или какую часть первое число составляет от второго.
Равенство двух отношений называют пропорцией.
В пропорции а/в=с/д числа а и д называют крайними членами пропорции , числа в и с –средними членами пропорции.
В верной пропорции произведение крайних членов равно произведению средних .
Если произведение крайних членов пропорции равно произведению средних членов пропорции , то пропорция верна. Это свойство называют основным свойством пропорции.
Две величины называют прямо пропорциональными , если при увеличении ( уменьшении ) одной из них в несколько раз другая увеличивается ( уменьшается ) во столько же раз.
Две величины называют обратно пропорциональными , если при увеличении ( уменьшении ) одной из них в несколько раз другая уменьшается ( увеличивается ) во столько же раз.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
Длина окружности и площадь круга.
Замкнутая линия все точки которой лежат на одинаковом расстоянии от одной точки «О»,называется окружностью.
Ту часть плоскости , которая лежит внутри окружности ( вместе с самой окружностью), называют кругом.
Точку «О» называют центром окружности и круга.
Отрезок соединяющий точку окружности с центром называют радиусом. Все радиусы одной окружности равны.
Отрезок соединяющий две точки окружности и проходящий через центр окружности называется диаметром. Диаметр состоит из двух радиусов , поэтому диаметр окружности в 2 раза длиннее ее радиуса.
Диаметр делит круг на 2 полукруга , а окружность – на 2 полуокружности.
Часть окружности между двумя точками называют дугой окружности.
Длина окружности прямо пропорциональна длине её диаметра. Поэтому для всех окружностей отношение длины окружности к длине её диаметра является одним и тем же числом. Его обозначают греческой буквой П— пи . Формула длины окружности: С=п d или C=2пr. П= 3,1416…..
Все точки поверхности шара одинаково удалены от центра шара.
Отрезок, соединяющий точку поверхности шара с центром ,называют радиусом шара.
Отрезок , соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара.
Диаметр шара равен двум радиусам.
Поверхность шара называют сферой.
Рациональные числа.
Положительные и отрицательные числа.
Числа со знаком + называют положительными.
Числа со знаком – называют отрицательными.
Прямую с выбранными на ней началом отсчета , единичным отрезком и направлением называют координатной прямой.
Число, показывающее положение точки на прямой , называют координатой этой точки.
Два числа , отличающиеся друг от друга только знаками, называют противоположными числами.
Натуральные числа , противоположные числа и нуль называют целыми числами.
Модулем числа а называют расстояние ( в единичных отрезках) от начала координат до точки А(а).
Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу.
Противоположные числа имеют равные модули.
Сравнение чисел.
Любое отрицательное число меньше любого положительного числа.
Из двух отрицательных чисел меньше то, модуль которого больше.
Нуль больше любого отрицательного числа , но меньше любого положительного числа.
На горизонтальной координатной прямой точка с большей координатой лежит правее точки с меньшей координатой.
Сложение и вычитание положительных и отрицательных чисел.
Любое число от прибавления положительного числа увеличивается , а от прибавления отрицательного числа уменьшается.
Сумма двух противоположных чисел равна нулю.
Чтобы сложить два отрицательных числа , надо: а)сложить их модули; б) поставить перед полученным числом знак — .
Чтобы сложить два числа с разными знаками, надо: а) из большего модуля слагаемых вычесть меньший; б) поставить перед полученным числом знак того слагаемого , модуль которого больше.
Чтобы из данного вычесть другое ,надо к уменьшаемому прибавить число , противоположное вычитаемому: а-б=а+(-б)
Любое выражение содержащее лишь знаки сложения и вычитания , можно рассматривать как сумму.
Чтобы найти длину отрезка на координатной прямой ,надо из координаты его правого конца вычесть координату его левого конца.
Умножение и деление положительных и отрицательных чисел.
Чтобы перемножить два числа с разными знаками , надо перемножить модули этих чисел и поставить перед полученным числом знак — .
Чтобы перемножить два отрицательных числа , надо перемножить их модули.
Чтобы разделить отрицательное число на отрицательное , надо разделить модуль делимого на модуль делителя.
При делении чисел с разными знаками , надо: а) разделить модуль делимого на модуль делителя; б) поставить перед полученным числом знак — .
Рациональные числа.
Число , которое можно записать в виде отношения а/н , где а-целое число , а н-натуральное число , называют рациональным числом.
Любое целое число является рациональным.
Сумма , разность и произведение рациональных чисел тоже рациональные числа.
Если делитель отличен от нуля , то частное двух рациональных чисел тоже рациональное число.
Любое рациональное число можно записать либо в сиде десятичной дроби ( в частности целого числа ) , либо в виде периодической дроби.
Сложение рациональных чисел обладает переместительным и сочетательным свойствами.
Умножение рациональных чисел тоже обладает переместительным и сочетательным свойствами.
Произведение может быть равно нулю лишь в том случае , когда хотя бы один из множителей равен нулю.
Умножение рациональных чисел обладает распределительным свойством относительно сложения.
Решение уравнений.
Если перед скобками стоит знак + , то можно опустить скобки и этот знак + , сохранив знаки слагаемых , стоящих в скобках.Если первое слагаемое записано без знака , то его надо записать со знаком + .
Чтобы раскрыть скобки перед которыми стоит знак — , надо заменить этот знак на + , поменяв знаки всех слагаемых в скобках на противоположные , а потом раскрыть скобки.
Подобные слагаемые.
Если выражение является произведением числа и одной или нескольких букв , то это число называют числовым коэффициентом ( или просто коэффициентом ).
Слагаемые , имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Чтобы сложить ( или говорят : привести ) подобные слагаемые , надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Решение уравнений.
Корни уравнения не изменяются , если обе части уравнения умножить или разделить на одно и то же число , не равное нулю.
Корни уравнения не изменяются , если какое –нибудь слагаемое перенести из одной части уравнения в другую , изменив при этом его знак.
Уравнение , которое можно привести к виду ах=в с помощью переноса слагаемых и приведения подобных , называют линейным уравнением с одним неизвестным.
Координаты на плоскости.
Две прямые , образующие при пересечении прямые углы , называют перпендикулярными.
Отрезки ( или лучи) , лежащие на перпендикулярных прямых , называют перпендикулярными отрезками ( или лучами).
Две непересекающиеся прямые на плоскости называют параллельными.
Если две прямые в плоскости перпендикулярны третьей , то они параллельны.
Через каждую точку плоскости , не лежащую на данной прямой , можно провести только одну прямую , параллельную данной прямой.
Отрезки ( или лучи) , лежащие на параллельных прямых , называют параллельными отрезками ( или лучами).
Системой координат на плоскости называют две перпендикулярные координатные прямые- х и у , которые пересекаются в начале отсчета – точке О. Тока О называется началом координат.
Плоскость на которой выбрана система координат , называют координатной плоскостью.
Координатную прямую х называют осью абсцисс , а у – осью ординат.
Делителем Число 12 имеет шесть | |
Кратным Первые пять чисел, | |
Признаки делимости На Если На Если На Если На Если На Если запись натурального | |
Число, Число, имеющее более | |
Наибольшее Чтобы 1.)Разложить 2.)Из 3.)Найти Натуральные числа | |
Наименьшим Чтобы 1.)Разложить 2.)Выписать 3.)Добавить 4.)Найти произведение | |
| Основное Если числитель и |
| Деление числителя |
60 = 2 168 = 2 Наименьший 2 · 2
| Чтобы 1.)Найти 2.)Разделить 3.)Умножить числитель |
Чтобы 1.)Привести 2.)Сравнить (сложить, | |
5 | Чтобы 1.)Привести 2.)Отдельно выполнить |
3 | Чтобы 1.)Привести 2.)Отдельно выполнить |
| Чтобы Чтобы 1.)Найти 2.)Первое Чтобы выполнить |
| Чтобы найти дробь |
| Два числа, произведение |
| Чтобы разделить |
| Чтобы найти число |
| Частное двух чисел |
a:b=c:d a·d=b·c | Равенство Числа В Если произведение |
4 : 2 = 7 : 21 5 : 25 = 7 : 35 | Две Если две величины |
Две Если две величины | |
Отношение 1 : 100000 = | |
C = 2·π·r | Длина r – π = 3,14 |
S = π·r2 | Площадь r – π = 3,14 |
| Прямую, Число, показывающее |
2,6 и
| Два Натуральные числа, |
| Модулем числа a |
– 8,7 + (– 3,5) = – (8,7 + | Чтобы 1.)Сложить 2.)Поставить перед |
6,1 + или 6,1 + (– 4,2) = 6,1 – 4,2 = | Чтобы 1.)Из 2.)Поставить перед |
Если A(9) | Чтобы найти длину |
(–1,2)·0,3 = | Чтобы перемножить |
(–3,2)·( –9) = | Чтобы перемножить |
(–12) : ( –4) = 12 : 4 = 3 | Чтобы разделить |
3,6 : (–3) = –(3,6:3) = –1,2 | При 1.)Разделить 2.)Поставить перед |
x = | Число x, которое можно |
16–(10–18+12) = | Чтобы раскрыть |
0,3a·(–0,7b) | Если выражение |
2m – 7m + 3m | Слагаемые, Чтобы сложить (или |
Свойства 1.)Корни 2.)Корни уравнения | |
| Две прямые, образующие |
| Две Если Через каждую точку |
|
О – (3;5) – |
Справочный материал «Математика 6 класс»
С переходом в 6 класс учащиеся сталкиваются с большим объёмом информации по всем предметам, что, конечно, пугает и настораживает детей. В такие моменты очень важно помочь ученикам быть готовыми к усвоению новых тем и при этом не забывать уже пройденный материал. Ведь всем понятно, к чему приводят пробелы, даже малейшие, в знаниях. Что может быть лучше, чем чётко структурированный и компактно собранный материал по всему курсу? Именно такой материал мы подготовили вам в помощь.

Справочный материал «Математика 6 класс» содержит основные определения, свойства и правила за курс математики в 6 классе. Его можно использовать в качестве раздаточного материала для закрепления темы, а также как памятку с основными моментами, которую учащиеся могут распечатать для себя.
Весь материал собран в том порядке, в котором он даётся для изучения по программе. Здесь вы увидите:
- материал, собранный по разделу «Делимость чисел»;

- информацию по разделу «Обыкновенные дроби и действия с ними»;

- материал, связанный с разделом «Отношения и пропорции»;

- информацию по разделу «Рациональные числа и действия с ними»;

- необходимые начальные сведения по геометрии.

Презентация по математике на тему:»правила по математике 5 и 6 класс»
Инфоурок
›
Математика
›Презентации›Презентация по математике на тему:»правила по математике 5 и 6 класс»
Описание презентации по отдельным слайдам:
1 слайд

Описание слайда:
Основные правила по математике 5 и 6 класс
2 слайд

Описание слайда:
Сложение и вычитание десятичных дробей 1) Чтобы сложить (вычесть) десятичные дроби надо: 2) Записать их столбиком запятая под запятой; 3) Уравнять количество знаков после запятой; 4) Сложить (вычесть) числа, не обращая внимания на запятую; 5)В ответе поставить запятую под запятой в данных дробях. 3,700 64,340 2,651 5,425 6,351 58,915
3 слайд

Описание слайда:
Умножение десятичных дробей 1) Чтобы перемножить две десятичные дроби надо: 2) Записать их столбиком не обращая внимания на запятые; 3) Выполнить умножение, не обращая внимания на запятые; 4) В ответе отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителей вместе. 0,2 5 4 3,1 4 0,0 3 2,5 0,0 0 7 6 2 1 5 7 0 6 2 8 7,8 5 0
4 слайд

Описание слайда:
Деление десятичной дроби на натуральное число. 1) Чтобы разделить десятичную дробь на натуральное число надо: 2) Сначала выполнить деление целой части; 3) Поставить в частном запятую , когда закончится деление целой части, 4) Выполнить деление, при необходимости дописать нули. 7, 5 0 6 0,3 2 8 6 1, 2 5 0 0, 0 4 1 5 0 3 1 2 0 3 0 3 2 3 0 3 2 0
5 слайд

Описание слайда:
Деление на десятичную дробь. 1) Чтобы разделить число на десятичную дробь надо: 2) В делимом и в делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе; 3)После этого выполнить деление на натуральное число. 1 2, 0 9 6 : 2, 2 4 = 1 2 0 9, 6 : 2 2 4 = 5, 4 1 2 0 9, 6 2 2 4 1 1 2 0 5, 4 8 9 6 8 9 6 0
6 слайд

Описание слайда:
7 слайд

Описание слайда:
Правило решения уравнения 1) Раскрыть скобки. 2) Перенести слагаемые с буквой в левую часть уравнения, без буквы – в правую часть 3) Привести подобные слагаемые. 4) Разделить левую и правую части уравнения на множитель перед буквой. Образец а) 8 – 5х = 13 – 3х б) 2(х+3) – 5 = 4 – (х-9) — 5х + 3х = 13 — 8 2х + 6 — 5 = 4 – х +9 — 2х = 5 2х + х = 4 + 9 – 6 + 5 х = 5 : (-2) 3х = 12 х = — 2,5 х = 12 : 3 х = 4
8 слайд

Описание слайда:
Сумма чисел Чтобы сложить два числа с ОДИНАКОВЫМИ знаками надо: 1) Поставить знак слагаемых, 2) Сложить их модули. Чтобы сложить два числа с РАЗНЫМИ знаками надо: 1)Поставить знак того слагаемого, модуль которого больше, 2) Из большего модуля слагаемых вычесть меньший
9 слайд

Описание слайда:
Умножение и деление чисел Чтобы умножить или разделить два числа с ОДИНАКОВЫМИ знаками надо: 1) Поставить знак плюс, 2) Умножить или разделить их модули. Чтобы умножить или разделить два числа с РАЗНЫМИ знаками надо: 1) Поставить знак минус, 2) Умножить или разделить их модули.
10 слайд

Описание слайда:
Действия с относительными числами (план ответа) Вопросы 1) Какое действие? 2) каких чисел? 3) Какой знак в ответе? 4) Каким действием найти модуль? Ответы на вопросы на 1) сумма, умножение или деление, На 2) одинаковых знаков или разных знаков, На 3) плюс или минус На 4) сложением, вычитанием, умножением или делением.

Курс профессиональной переподготовки
Учитель математики

Курс повышения квалификации
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс:
Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник:
Все учебники
Выберите тему:
Все темы
также Вы можете выбрать тип материала:

Краткое описание документа:
Есть только два направления изменения человека – развитие либо деградация. Поэтому, если образование не способствует развитию, то оно служит деградации.
В последние года аттестация учащихся девятых классов идет в форме ОГЭ. Результаты неутешительные. Одной из основных причин плохой сдачи экзамена является плохой навык в выполнении действий. В курсе математики начальной школы, я считаю, учащиеся должны идеально знать таблицу умножения, должно уже появиться «чувство числа». В курсе математики в основном правила удобно строить в виде алгоритма по выполнению (первое, второе, и т.д. ). Это способствует более быстрому овладению счетом. Немаловажную роль играет также и образец выполнения примеров и заданий.
Общая информация
Номер материала:
461314
Похожие материалы
Оставьте свой комментарий

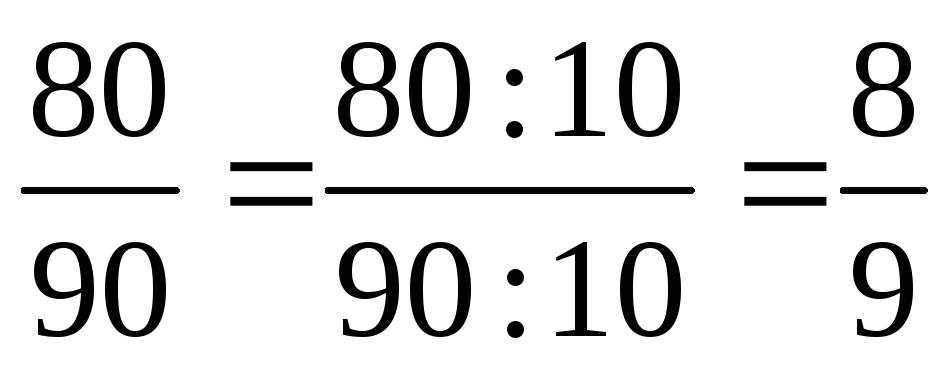




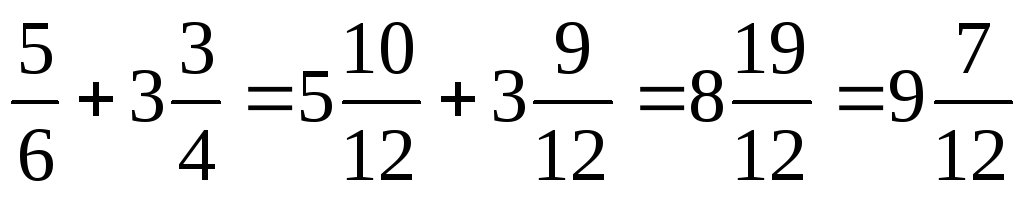










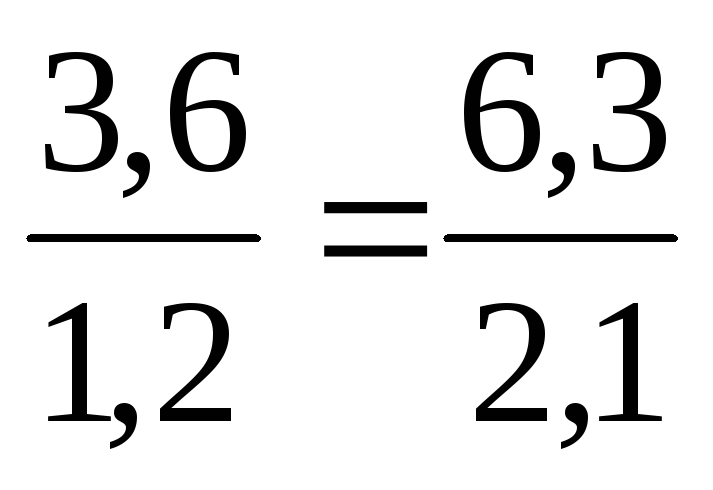
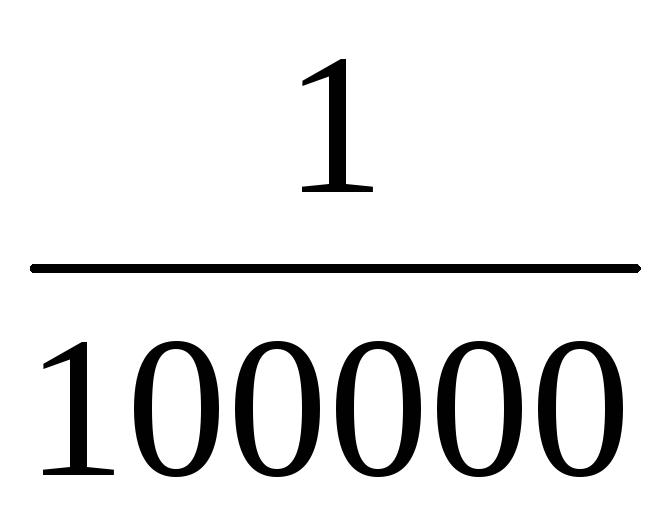



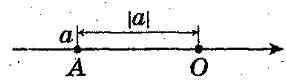
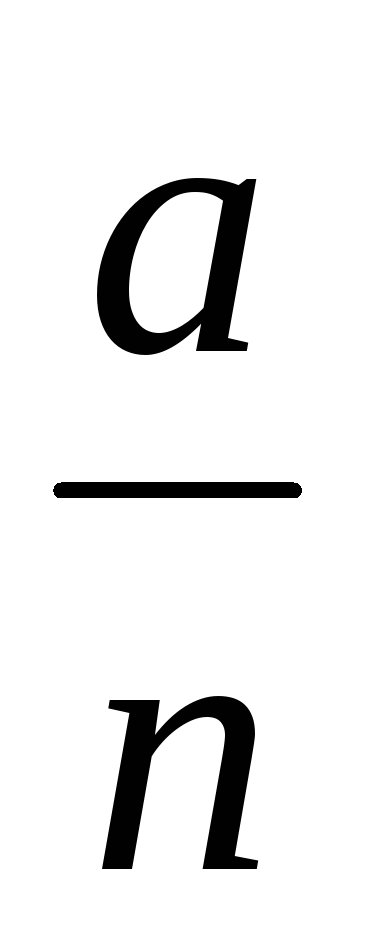
 ,
,
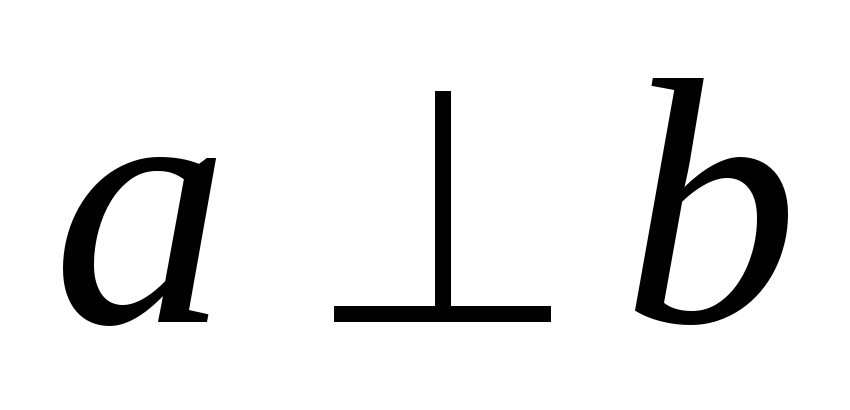 ).
).
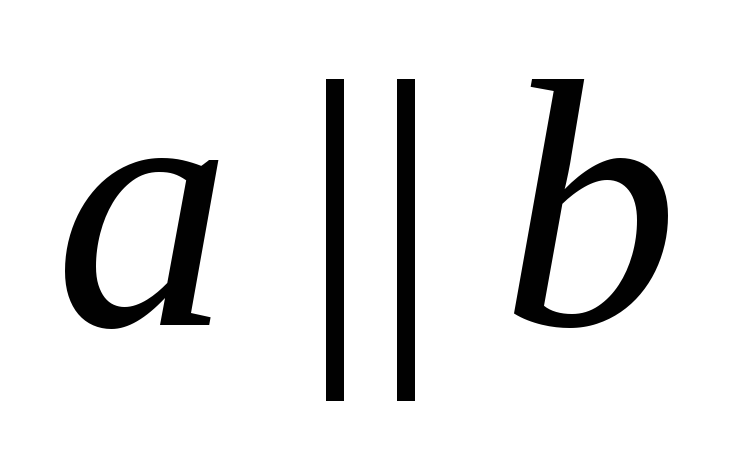 ).
).