Олимпиадные задачи с решением для учащихся 5-6 классов
Текст этой презентации
Слайд 1

Презентацию подготовила учитель математики МБОУ «Федоровская СОШ №2 с углублённым изучением отдельных предметов» Вдовенко Ирина Викентьевна
Осенняя сессия
5-6 классы
Слайд 2

М А Т Е М А Т И Ч Е С К И Е И Г Р Ы
Задача 1. Двое по очереди берут из кучи камни. Разрешается брать любую степень двойки (1, 2, 4…). Взявший последний камень выигрывает. Кто победит в этой игре?
Слайд 3
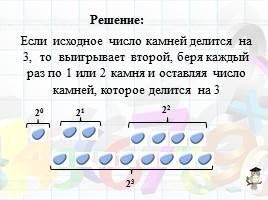
Если исходное число камней делится на 3, то выигрывает второй, беря каждый раз по 1 или 2 камня и оставляя число камней, которое делится на 3
Решение:
20
22
21
23
Слайд 4

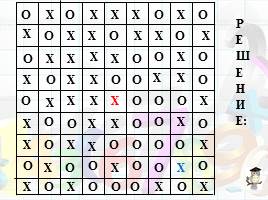
Задача 2. Двое играют, поочередно выставляя крестики и нолики на квадратном поле 9х9. В конце каждый получает очко за каждую строку и столбец, в которых его знаков больше. Сможет ли первый игрок выиграть?
Слайд 5
Х
О
Х
О
Х
О
О
О
О
О
О
О
О
О
О
Х
Х
Х
Х
Х
Х
Х
Х
Х
Х
О
О
О
О
О
О
О
О
О
О
Х
Х
Х
Х
Х
Х
Х
Х
Х
Х
О
О
О
О
О
О
О
О
О
О
Х
Х
Х
Х
Х
Х
Х
Х
Х
Х
Х
Х
Х
Х
Х
Х
Х
Х
О
О
О
О
О
О
О
О
Р
Е
Ш
Е
Н
И
Е:
Слайд 6

Задача 3. Двое играющих по очереди красят полоску из 150 клеток: первый всегда красит две клетки подряд, а второй — три. Проигрывает тот, кто не может сделать ход. Кто должен выиграть при правильной игре?
Слайд 7

Решение:
Первый. В какой-то момент (можно на первом ходу) он оставляет незакрашенный просвет в две клетки и не трогает его, пока есть не менее трёх незакрашенных клеток подряд.
Слайд 8

Ч И С Л О В Ы Е З А Д А Ч И
Требуется расшифровать запись арифметического равенства, в котором цифры заменены буквами, причем разные цифры заменены разными буквами, одинаковые — одинаковыми. Предполагается, что исходное равенство верно и записано по обычным правилам арифметики. В частности, в записи числа первая слева цифра не является цифрой 0; используется десятичная система счисления.
Слайд 9

№1 Животноводческий ребус.
Б + Б Е Е Е = М У У У
Так как при сложении данных чисел цифра Е в разряде десятков поменялась на цифру У, то суммой однозначных чисел Б и Е является двузначное число, начинающееся с единицы. Так как помимо увеличения на единицу цифры в разряде десятков также изменилась и цифра в разряде сотен, то Е = 9, Б = 1, У = 0. Ответ.1 + 1999 = 2000.
Слайд 10

№2 Нитки и ткань.
НИТКА + НИТКА ТКАНЬ
Ответ: 15306 + 15306 = 30612.
Слайд 11

№3 Вагоны.
ВАГОН + ВАГОН = СОСТАВ
Ответ: 85679 + 85679 = 171358.
Слайд 12

№4 Собака и кошки.
КОШКА + КОШКА + КОШКА = СОБАКА
Ответ: Первый вариант: 56350 +56350 + 56350 = 169050 Второй: 57350 + 57350 + 57350 = 172050
Слайд 13

№5. Ищем зеркальную пару чисел.
Два числа называются зеркальной парой чисел, если порядок цифр в одном из них слева направо такой же самый, как порядок цифр другого числа справа налево.
Произведение какой зеркальной пары чисел равно 92565?
Ответ: 165 и 561
Слайд 14

Решение: Ясно, что числа зеркальной пары будут трехзначными: abc · cba=92565 Первый вывод: a=5 (последняя цифра произведения =5), с-должно быть нечетное и меньше 3, иначе 5b3 · b5 > 92565 следовательно с=1. Получим: 1b5 5b1 1b5 ??b*5 ?b* 55 9 2 5 6 5 Из суммы второго столбца b+(b*5)=?6 или 6*b=?6, следовательно b=1 или 6. Получим либо 115 и 511, либо 165 и 561, перемножив находим , что подходит 165 и 561.
Слайд 15

Принцип Дирихле
Запишем принцип Дирихле: если по N разложить предметы, число которых M больше N, то найдется ящик, в котором будет находится больше одного предмета.
На первый взгляд непонятно, почему это совершенно очевидное предложение, тем не менее, является мощным математическим методом решения задач, причем, самых разнообразных. Дело в том, что в каждой конкретной задаче нелегко понять, что же здесь выступает в роли «предметов», а что – в роли «ящиков».
П Р И Н Ц И П Д Е Р И Х Л Е
Слайд 16

1тип задач «Сколько нужно взять?..»
1. В мешке лежат шарики двух разных цветов. Какое наименьшее число шариков нужно вынуть из мешка, чтобы среди ни обязательно оказались два шарика одного цвета?
Решение:
Здесь роль предметов играют шарики (М=?), роль ящиков — цвета (N=2).Чтобы M>N, т.е. в одном ящике оказалось два предмета, их должно быть больше двух, т.е. М=3
1тип задач «Сколько нужно взять?..»
Слайд 17

2. В коробке лежат карандаши: 7 красных и 5 синих. В темноте берут карандаши. Сколько карандашей надо взять, чтобы среди них было не менее 2 красных и не менее 3 синих?
Решение: Если предположить, что сначала будут попадаться только красные карандаши, то для того, чтобы было 3 синих, нужно взять 7(красные)+3(N)=10. Это «худший» вариант развития событий, т.к. красных карандашей больше.
Слайд 18

2 тип задач «Докажите, что найдутся двое…»
1. При каком наименьшем количестве учеников школы среди них обязательно найдутся двое, у которых день и месяц рождения совпадают?
Решение: Дней в году N=365 или 366,то принципу Дирихле М= 366 или 367.
2 тип задач «Докажите, что найдутся двое…»
Слайд 19

2 тип задач «Докажите, что найдутся двое…»
2. В лесу растет миллион елок. Известно, что на каждой из них не более 600 000 иголок. Докажите, что в лесу найдутся хотя бы две елки с одинаковым числом иголок.
Решение: Если предположить, что у всех елок разное количество иголок, то таких елок 600 000 (это ящики, N= 600 000), а по условию елок 1000 000=М, то М>N,по принципу Дирихле найдутся хотя бы две елки «в одном ящике», т.е. с одинаковым количеством иголок.
Слайд 20

3 тип задач. Обобщенный принцип Дирихле:
1. В магазин привезли 25 ящиков с яблоками трех сортов, причем в каждом ящике лежали яблоки какого-то одного сорта. Можно ли найти 9 ящиков с яблоками одного сорта?
Решение. 25:3=8 (ост.1). 25=8*3+1. к=3, N=8, M>N, то принципу Дирихле найдутся хотя бы один ящик, в котором находятся более, чем к=3 предметов, т.е. 4 предмета.
3 тип задач. Обобщенный принцип Дирихле:
Слайд 21

3 тип задач. Обобщенный принцип Дирихле:
2. На площадке 20 собак восьми разных пород. Докажите, что среди них есть не менее трех собак одной породы.
Решение: 20:8=2(ост. 4), 20=8*2+4. к=2,N=8, М>N, то по принципу Дирихле найдутся хотя бы три собаки одной породы.
Слайд 22

Принцип Дирихле
вывод:
Таким образом, применяя данный метод, необходимо:
1)Определить, что удобно в задаче принять за «предметы», а что за «ящики».
2)Получить «ящики».Чаще всего, их должно быть больше, чем предметов.
3)Выбрать для решения требуемую формулировку принципа Дирихле.
Слайд 23

Задача 1. Три клоуна Бим, Бам и Бом вышли на арену в красной, зеленой и синей рубашках. Их туфли были тех же цветов. У Бима цвета рубашки и туфель совпадали. У Бома ни туфли, ни рубашка не были красными. Бам был в зеленых туфлях, а в рубашке другого цвета. Как были одеты клоуны?
Л О Г И Ч Е С К И Е З А Д А Ч И
Слайд 24

Ответ: Бим одет в красную рубашку и красные туфли, Бам в синей рубашке и зеленых туфлях, Бом в зеленой рубашке и туфлях синего цвета.
Решение:
Слайд 25

Задача 2. Три курицы снесли за три дня три яйца. Сколько яиц снесут двенадцать кур за двенадцать кур за двенадцать дней?
Слайд 26

Три курицы снесли за 3 дня 3 яйца, следовательно, 3 крицы снесут за 12 дней в 4 раза больше яиц, а 12 кур за 12 дней еще в 4 раза больше, т.е. 48 яиц. Решение задачи удобно записать в виде таблицы: Количество кур Количество дней Количество яиц 3 3 3 3 12 3х4=12 12 12 12х4=48
Решение:
Слайд 27

Задача 3. Когда отцу было 27 лет, сыну было 3 года. Сейчас сыну в три раза меньше лет, чем отцу. Сколько лет каждому из них?
Решение:
Разница в возрасте между отцом и сыном неизменна и равна 24 годам. Сыну в три раза меньше лет, чем отцу, поэтому 24 года — это удвоенный возраст сына. Следовательно, сыну сейчас 12 лет, а отцу 36 лет.
Слайд 28

З А Д А Ч И Н А П Р О Ц Е Н Т Ы
Задача 1. Собрали 100 кг грибов. Оказалось, что их влажность 99%. Когда грибы подсушили, влажность снизилась до 98%. Какой стала масса этих грибов после подсушивания?
Решение:
В 100 кг грибов содержится, по условию, 99 кг воды и 1 кг сухого вещества. После подсушивания сухое вещество стало составлять 2% .Но если 2% составляют 1 кг, то вся масса грибов равна 50 кг.
Слайд 29

Задача 2. Возраст брата составляет 40% от возраста сестры. Сколько процентов составляет возраст сестры от возраста брата?
Решение:
Примем возраст сестры за 100%.Возраст брата составит 40%.
Процентное отношение возраста сестры к возрасту брата равно: (100/40) · 100% = 250%.
Слайд 30

Задача 3. В начале года число мужчин, работавших на заводе, составляло 40% от общей численности работников завода. После того, как были приняты на работу еще 6 мужчин, а 5 женщин уволилось, число мужчин и женщин на заводе сравнялось.Сколько человек работало на заводе в начале года?
Слайд 31

Решение: Число мужчин, работавших на заводе в начале года, было на 11 меньше числа работавших там женщин. Процентная разность между числом женщин и числом мужчин составляла в начале года 20%. Общая численность работавших на заводе в это время — 11:0,2 = 55 человек.
Слайд 32

З А Д А Ч И Н А Д Е Л И М О С Т Ь
Задача 1. Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18. На какое число делили?
Решение:
Из условия следует, что 100-4=96 делится на искомое число. Также 90-18=72 делится на искомое число.Их разность также делится на искомое число: 96-72=24. Следовательно, искомое число — 24, так как на него делится и 96, и 72.
Слайд 33

Задача 2. На каждой кочке в маленьком болотце сидят не меньше , чем по 3 лягушки, а всего лягушек — 145 .Тогда число кочек в этом болотце не может равняться:
( A )1; (B) 23; (C) 31; ( D ) 44; ( E ) 55;
Решение:
Разделим 145 на 3 и узнаем максимальное количество кочек в болотце, когда на каждой из них разместится не меньше 3 лягушек и получим 48.Перебирая ответы , остановимся на ответе (Е), как на единственном (55 больше 48).Ответ: 55.
Слайд 34

Задача 3. У двузначного числа «n» цифра десятков в два раза больше, чем цифра единиц. Тогда число «n» обязательно:
( A ) четное; (B) нечетное(C) меньше 20;
( D ) делится на 3; ( E ) делится на 6.
Решение:
Ищем число «n» среди ряда чисел: 10 — 99.По условию, у всех подозреваемых чисел — десятки четны (2,4,6,8), а единицы — в два раза меньше (1,2,3,4,).Перечислим все эти числа: 21, 42, 63, 84. Все они делятся на 3.Следовательно верен ответ (D).
Слайд 35

З А Д А Ч И С Г Е О М Е Т Р И Ч Е С К И М
С О Д Е Р Ж А Н И Е М
Задача 1. Сколько углов образуют 5 различных лучей, направленных из одной точки?
Решение:
Принцип решения следующий:
n – количество лучей, но каждый последующий луч образует еще один угол, следовательно искомое количество углов ищем по формуле
Ответ: 20 углов
Слайд 36
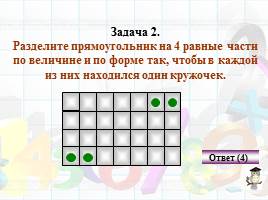
Задача 2. Разделите прямоугольник на 4 равные части по величине и по форме так, чтобы в каждой
из них находился один кружочек.
Ответ (4)
Слайд 37

Задача 3. Преуспевающий торговец
недвижимостью купил 16 акров
земли. Он решил разбить площадь
на 16 одноакровых участков под жилые
дома так, чтобы все участки были одного
размера и той же формы, что и основной
участок. Как это сделать?
Ответ
Слайд 38
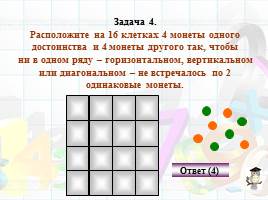
Задача 4. Расположите на 16 клетках 4 монеты одного
достоинства и 4 монеты другого так, чтобы
ни в одном ряду – горизонтальном, вертикальном
или диагональном – не встречалось по 2 одинаковые монеты.
Ответ (4)
Слайд 39

Задача 5. Разделите прямоугольный треугольник
на четыре равных треугольника.
Ответ
Слайд 40
Делаем вывод
Слайд 41

Задача 6. Разделите произвольный треугольник
на девять равных треугольника.
Ответ
Слайд 42

Задача 7. Не отрывая карандаша от бумаги и не
проводя по линии дважды, нарисуйте
фигуру, изображённую на рисунке.
Например
Слайд 43

Олимпиадные задания по математике (5, 6 класс): Задания для школьного этапа Всероссийской олимпиады школьников по математике для 5-6 классов
Задания школьного этапа Всероссийской олимпиады школьников
Пятый класс
1. Расшифруйте ребус, в котором одинаковым буквам соответствуют одинаковые цифры.
А Б В
+ В В
А А Б
2. В деревне Простоквашино на скамейке перед домом сидит дядя Федор, кот Матроскин, пес Шарик и почтальон Печкин. Если Шарик, сидящий крайним слева, сядет между Матроскиным и Федором, то Федор окажется крайним слева. Кто где сидит?
3.Три подруги вышли погулять. Одна из них была в красном, другая – в желтом, а третья — в синем платье. Их сумочки из тех же цветов. Известно, что только у Лизы цвет платья и сумочки совпадают. Ни платье, ни сумочка Олеси не были красными, Полина была с желтой сумочкой. Определи цвет платья и сумочки каждой девочки.
Платье | Сумка | |||||
Красное | Желтое | Синее | Красная | Синяя | Желтая | |
Лиза | ||||||
Олеся | ||||||
Полина | ||||||
4. Автор сказки «Красная шапочка» француз Шарль Перро родился в 1628 году, автор «Сказки о рыбаке и рыбке» А.С.Пушкин родился на 171 год позже, а автор сказки «Три медведя» Л.Н.Толстой родился на 29 лет позже А.С.Пушкина. Сколько лет прошло со дня рождения авторов любимых детских сказок до наших дней?
5. Взять четыре спички так, чтобы получилось (осталось) 5 квадратов.
О Т В Е Т Ы
ШКОЛЬНОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
5 класс
1.(6 баллов) Расшифруйте ребус, в котором одинаковым буквам соответствуют одинаковые цифры.
А Б В
+ В В
А А Б
Ответ. Вариантов ответов несколько, например 321 + 11 = 332. А = 3, Б = 2, В = 1 или 642+22=664( 6 баллов за каждый вариант)
2. (6 баллов) В деревне Простоквашино на скамейке перед домом сидит дядя
Федор, кот Матроскин,пес Шарик и почтальон Печкин. Если Шарик, сидящий крайним слева,сядет между Матроскиным и Федором, то Федор окажется крайним слева. Кто где сидит?
Ответ. Слева направо сидят: Шарик,Федор,Матроскин,Печкин
3.(6 баллов) Три подруги вышли погулять. Одна из них была в красном, другая – в желтом, а третья — в синем платье. Их сумочки из тех же цветов. Известно, что только у Лизы цвет платья и сумочки совпадают. Ни платье, ни сумочка Олеси не были красными, Полины была с желтой сумочкой. Определи цвет платья и сумочки каждой девочки.
Ответ. У Лизы — красное платье и красная сумочка; у Олеси — желтое платье и синяя сумочка; у Полины– синее платье и желтая сумочка.
Решение. Представим в виде таблицы решение задачи.
Полина была с желтой сумочкой. Значит, у неё не было красной и синей сумочек. А у Лизы и Олеси не было желтой сумочки.
Платье | Сумка | |||||
Красное | Желтое | Синее | Красная | Синяя | Желтая | |
Лиза | — | |||||
Олеся | — | |||||
Полина | — | — | + | |||
Ни платье, ни сумочка Олеси не были красными
Платье | Сумка | |||||
Красное | Желтое | Синее | Красная | Синяя | Желтая | |
Лиза | — | |||||
Олеся | — | — | — | |||
Полина | — | — | + | |||
Значит красная сумочка у Лизы. И красное платье у Лизы.
Платье | Сумка | |||||
Красное | Желтое | Синее | Красная | Синяя | Желтая | |
Лиза | + | — | — | + | — | — |
Олеся | — | — | + | — | ||
Полина | — | — | — | + | ||
Платье | Сумка | |
Лиза | Красное | Красная |
Олеся | Желтое | Синяя |
Полина | Синее | Желтая |
4.(6 баллов) Автор сказки «Красная шапочка» француз Шарль Перро родился в 1628 году, автор «Сказки о рыбаке и рыбке» А.С.Пушкин родился на 171 год позже, а автор сказки «Три медведя» Л.Н.Толстой родился на 29 лет позже А.С.Пушкина. Сколько лет прошло со дня рождения авторов любимых детских сказок до наших дней?
Ответ. 386,215,186 лет
Решение.
Перро-1628
Пушкин -1628+171=1799
Толстой -1628+171+29=1828
2014-1628=386лет прошло со дня рождения Ш.Перро
2014-1799=215 лет прошло со дня рождения А.С.Пушкина
2014-1828=186 лет прошло со дня рождения Л.Н.Толстого
5.( 6 баллов) Взять четыре спички так, чтобы получилось (осталось) 5 квадратов.
Ответ.
6. (6 баллов)
Решение. Волку надо бежать до домика Наф-Нафа 4+6:2=7(мин), а поросятам 6 мин. 6меньше 7, значит поросята успеют добежать до домика Наф-Нафа.
Ответ.Успеют
Шестой класс
1.В записи (88888888) нужно поставить знаки сложения таким образом, чтобы получилась сумма, которая будет равна 1000.
2. Малыш, Алиса, Кай и Женя заняли первые четыре места в соревнованиях, причем никто из них не делил между собой какие-нибудь места. Известно:
- Малыш не был ни первым, ни четвертым.
- Алиса заняла второе место.
- Кай не был последним.
Какое место занял каждый?
3. Мама дала Зое денег ,чтобы она в школьном буфете купила завтрак.
Когда Зоя вер вернулась из школы, то перед мамой отчиталась так: «1/2 всех денег я истратила на бумагу,1/5 -на чай, а 3/10 -на конфеты». Мама догадалась, что дочь истратила все деньги. Как она узнала ?
4. «Змей Горыныч побежден!»-такая молва дошла до Микулы Селяниновича. Он знал, что мог это сделать либо Илья Муромец, либо Алеша Попович, либо Добрыня Никитич. Вскоре Микуле сообщили:
1)Змея Горыныча победил не Илья Муромец;
2)Змея Горыныча победил Алеша Попович.
Спустя некоторое время выяснилось, что одно их этих сообщений неверное, а другое верное. Догадайтесь, кто из трех богатырей победил Змея Горыныча.
5.Трое рыбаков поймали 75 карасей. Стали варить уху. Когда один дал 8 карасей, а другой 12, а третий-7, то карасей у них стало поровну. Сколько карасей поймал каждый рыбак?
6. Имеется 8 палочек длиной в 1см, 8 палочек длиной в 2см и 7 палочек длиной в 5 см.
Можно ли из всех палочек этого набора сложить прямоугольник?
Разламывать палочки нельзя.
.
О Т В Е Т Ы И РЕШЕНИЯ
ШКОЛЬНОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
6 класс
1. (6 баллов) В записи (88888888) нужно поставить знаки сложения таким образом, чтобы получилась сумма, которая будет равна 1000.
Решение:
Способ 1: 88+8+8+8+888=1000
Способ 2: 8+8+888+88+8=1000.
2. (6 баллов) Малыш, Алиса, Кай и Женя заняли первые четыре места в соревнованиях, причем никто из них не делил между собой какие-нибудь места. Известно:
- Малыш не был ни первым, ни четвертым.
- Алиса заняла второе место.
- Кай не был последним.
Какое место занял каждый?
Ответ: Малыш-3, Алиса-2, Кай-1, Женя-4 место.
3. (6 баллов) Мама дала Зое денег ,чтобы она в школьном буфете купила завтрак. Когда Зоя вер вернулась из школы, то перед мамой отчиталась так: «1/2 всех денег я истратила на бумагу,1/5 -на чай, а 3/10 -на конфеты». Мама догадалась, что дочь истратила все деньги. Как она узнала?
Решение: 1/2+1/5+3/10=1, т.е. все деньги
4. (6 баллов) «Змей Горыныч побежден!»-такая молва дошла до Микулы Селяниновича. Он знал, что мог это сделать либо Илья Муромец, либо Алеша Попович, либо Добрыня Никитич. Вскоре Микуле сообщили:
1)Змея Горыныча победил не Илья Муромец;
2)Змея Горыныча победил Алеша Попович. Спустя некоторое время выяснилось, что одно их этих сообщений неверное, а другое верное. Догадайтесь, кто из трех богатырей победил Змея Горыныча.
Ответ. Добрыня Никитич.
Решение. Предположим, что Змея Горыныча победил Илья Муромец. Тогда оба сообщения неверные-результат не соответствует условию задачи. Предположим, что Змея Горыныча победил Алеша Попович.Тогда оба сообщения верные. И этот результат не соответствует условию задачи.
Предположим, что Змея Горыныча победил Добрыня Никитич.Тогда первое сообщение верное, а второе- неверное. Результат соответствует условию задачи
5. (6 баллов) Трое рыбаков поймали 75 карасей. Стали варить уху. Когда один дал 8 карасей , а другой 12, а третий-7, то карасей у них стало поровну. Сколько карасей поймал каждый рыбак?
Решение. 75-8-12-7=48(осталось всего окуней)
48 окуней на 3 рыбака.48:3=16
У каждого рыбака осталось по 16 окуней
16+ 8 = 24 — поймал 1 рыбак
16 + 12 = 28 — поймал 2 рыбак
16 + 7 = 23 — поймал 3 рыбак
Ответ: 24, 28, 23.
6. (6 баллов) Имеется 8 палочек длиной в 1см, 8 палочек длиной в 2см и 7 палочек длиной в 5 см. Можно ли из всех палочек этого набора сложить прямоугольник? Разламывать палочки нельзя.
Решение.
Если a и b – длины сторон прямоугольника, периметр P = 2(a+b), т. е. P – четное число в случае целых a и b.
8*1+8*2+7*5=8+16+35=59 (см) – нечетное число.
Поэтому из всех палочек данного набора прямоугольник сложить нельзя.
Ответ: нельзя
Олимпиадные задания по алгебре (6 класс) по теме: Олимпиады по математике в 5-6 классах, с содержанием задач на олимпийскую тематику.
Задания для 5 класса.
Каждая задача оценивается в 5 баллов.
- Найдите цифры, вместо которых стоят звездочки:
* 8 *
4 * 2
——-
7 * 0
* * *
* * * *
—————
* * * * 2 *
- На одной чаше весов лежат шесть одинаковых пачек чая и гиря массой 50г., а на другой – одна пачка чая и две гири массой 100 и 200 г. Весы находятся в равновесии. Определите, сколько граммов весит одна пачка чая?
- В олимпийской команде по конному спорту пять голов и четырнадцать ног. Сколько из них людей, а сколько лошадей?
- Разрежьте циферблат часов на три части так, чтобы сумма цифр
в каждой части была одинаковой.
- Талисманы олимпийских игр в Сочив 2014 году — Зайка, Белый Мишка и Леопард – после изнурительных тренировок сели пить чай. Белый Мишка и Зайка выпили вдвоём 11 чашек, Леопард и Белый Мишка — 15, а Зайка и Леопард — 14. Сколько чашек чая выпили все Зайка, Белый Мишка и Леопард вместе?
Решение.
- Указание: Усмотреть, что последняя цифра в первом числе – это 0 или 5, а первая цифра – 3, а затем перебрать несколько вариантов.
Ответ: 385·412=158620. - Решение: 1)100+200=300 грамм на одних весах.
2)300-50=250 грамм чая
3)250:(6-1)=50
Ответ: 50 г. - Ответ. 3 человека и 2 лошади.
Решение. Предположим сначала, что все пятеро – люди. Это 5 голов и 10 ног. Замена одного человека на лошадь дает +2 ноги. У нас пока что недостает 4 ноги. Значит, нужно 2 человека заменить лошадьми.
- Решение: Сумма всех цифр на циферблате равна 1+2+3+…+9+1+0+1+1+1+2=51. Значит, на каждой из частей сумма цифр должна быть равна 51:3=17.
- Ответ: 20 чашек
Решение:
Зайка + Белый Мишка =11 — по условию задачи
Леопард + Белый Мишка =15 — по условию задачи
Зайка + Леопард + 2 Белый Мишка =26,
Зайка + Леопард =14- по условию задачи
14+2Белый Мишка =26
2Белый Мишка =12
Белый Мишка =6
Зайка =5
Леопард =9
Белый Мишка + Зайка + Леопард =20
Олимпиадные задания по математике (5, 6 класс) на тему: Задания для школьной олимпиады (5-6 класс)
5 класс
Задача1.На скамейке сидит Маша, ее мама, бабушка и кукла. Бабушка сидит рядом с внучкой, но не рядом с куклой. Кукла не сидит рядом с мамой. Кто сидит рядом с мамой Маши?
(A) Маша; (B) бабушка; (C) Маша и бабушка; (D)Маша и кукла;
(E) бабушка и кукла
Задача 2. Сколько существует флагов, составленных из трех горизонтальных полос одинаковой ширины и различных цветов – белого, зеленого, красного и синего?
Задача3. Как из водопроводного крана, имея лишь два сосуда емкостью 3 и 5 литров набрать 4 литра воды?
Задача4. Восстановите отмеченные звездочками отсутствующие цифры
56*
*4
**72
*13*
1363*
Задача5. За три часа работы один экскаватор вынул 555 м3 земли. Сколько кубических метров земли вынет второй экскаватор за 4 часа, если в час он вынимает на 15 м3 больше, чем первый?
6 класс
Задача1. Четверо ребят обсуждали ответ к задаче. Коля сказал: «Это число 9». Роман: «Это простое число». Катя: «Это четное число». А Наташа сказала, что это число 15. Назовите это число, если одна девочка и один мальчик ошиблись ровно по одному разу.
( A )1; (B) 2; (C) 3; ( D ) 9; ( E ) 15;
Задача 2. Сколько существует флагов, составленных из трех горизонтальных полос одинаковой ширины и различных цветов – белого, зеленого, красного, синего и желтого?
Задача3. Как отмерить 15 минут, необходимых для варки
яиц при помощи песочных часов, отмеряющих 7 минут и 11 минут?
Задача4. С автовокзала вышел автобус со скоростью 60 км/ч. Через 0,5ч. вслед за ним вышла легковая автомашина со скоростью 75 км/ч. Через сколько часов после своего выезда легковая автомашина будет впереди автобуса на 45 км.?
Задача5. Отрезок, равный 28 см., разделен на три неравных отрезка. Расстояние между серединами крайних отрезков равно 16 см. Найдите длину среднего отрезка.
Олимпиада по математике. Геометрические задачи, ч. 1. 5-6 класс.
Олимпиады по математике. 5-6 класс. Геометрические задачи. Часть 1
Часть 1. Самые простые задачи.
Многие из них можно предложить и ученикам начальной школы, которые увлекаются математикой.
Задача 1.
В какой из изображённых в ответах фигур закрашена ровно половина площади?
Варианты ответа:
А: 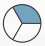 ; Б:
; Б: 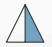 ; В:
; В:  ; Г:
; Г: 
Решение
Легко видеть, что ровно половина площади закрашена в ответе Б. В ответе А закрашена одна третья часть. В ответе Б — одна вторая, в ответе В — три четверти, в ответе Г — одна четверть.
Правильный ответ: Б
Задача 2
Разрежьте квадрат на 2 неравные части и сложите из них треугольник .
Решение:
Отрезать от квадрата треугольник, одна из сторон которого равна стороне квадрата, а другая-половине стороны квадрата. Из полученных треугольника и трапеции сложить треугольник.
Задача 3.
Миша разрисовал 9 квадратиков белым, серым и чёрным цветами так, как показано на рисунке. Какое наименьшее количество квадратиков надо перекрасить, чтобы никакие два квадратика, у которых общая сторона, не были одного цвета?

Решение
В правом верхнем углу есть 2 смежных серых квадратика. Чтобы выполнялось требование задачи, нужно перекрасить правый верхний квадратик в чёрный цвет, а в группе трёх чёрных квадратиков нужно нижний левый перекрасить в серый цвет. Итого 2 квадратика .
Задача 4
Квадрат со стороной 5 см разрезали на 25 равных квадратов. Составьте из них 2 квадрата.
Решение:
Один квадрат можно составить из 9 квадратов, а другой из 16.
Задача 5. Зелёная линия .
На рисунке изображена часть клетчатой доски. Площадь каждой клетки на ней равна 4 см2. Чему равна длина толстой зеленой линии?

Решение
Если площадь квадрата равна 4 см2, то его сторона равна 2 см (так как 2х2 = 4). Внимательно подсчитаем, через сколько сторон квадратиков пройдёт зелёная линия. Она проходит через 9 сторон. Значит, её длина равна 9х2 = 18 см.
Задача 6
Можно ли шахматную доску разрезать на равные фигуры, состоящие из трех клеточек, образующих «уголок»?
Решение:
Нельзя.
Шахматная доска состоит из 64 клеток. 64:3=21 ( ост 1). Одна клетка лишняя.
Задача 7.
Летела стая гусей. Впереди вожак, затем 2 гуся, затем 3 гуся и т. д. ( Построение стаи напоминало треугольник). Вечером гуси остьановились на ночлегш. Их расположение напоминало квадрат. В каждом ряду одинаковое количество гусей, причем число гусей в каждом ряду равно числу рядов. Гусей в стае меньше 50. Сколько гусей в стае?
Ответ:
36 гусей.
Использованы задачи из различных сборников олимпиадных заданий:
Евдокимов М.А. От задачек к задачам. М.: МЦНМО, 2004
Игнатьев Е.И. В царстве смекалки. М.: «Наука», 1987
Русанов В. Н. Математические олимпиады младших школьников.
Материалы международного конкурса «КЕНГУРУ»
Олимпиадные задания по математике (школьный этап 6 класс)
Олимпиадные задания
по математике для проведения школьного этапа
Всероссийской олимпиады школьников в 2017 — 2018 учебном году.
( 6 класс)
Задание №1
Вася может получить число 100, используя десять троек, скобки и знаки арифметических действий:
100 = (33 : 3 — 3 : 3) · (33 : 3 — 3 : 3). Улучшите его результат: используйте меньшее число троек и получите число 100.
Задание №2.
Малыш, Алиса, Кай и Женя заняли первые четыре места в соревнованиях, причем никто из них не делил между собой какие-нибудь места. Известно:
Малыш не был ни первым, ни четвертым.
Алиса заняла второе место.
Кай не был последним.
Какое место занял каждый?
Задание №3.
Прямоугольное поле ABCD состоит из четырех меньших прямоугольных полей (см. рисунок), три из которых имеют площади 10, 20, 30. Чему равна площадь поля ABCD?
- 30
Задание №4
Какова масса рыбы, если масса ее головы и туловища вместе 10 кг, туловища и хвоста – 8 кг, а головы и хвоста – 6 кг?
Задание №5
Отец старше сына в 4 раза, при этом суммарный их возраст составляет 50 лет. Через сколько лет отец станет старше сына в 3 раза?
Общие положения о проверке работ
Приведённые ниже решения задач не являются единственно возможными. Участники, вероятно, найдут и другие верные решения. При проверке и оценке решения учитывается только его верность и полнота. Приведённые ниже критерии по проверке задач также носят рекомендательный характер и могут быть уточнены и дополнены школьным жюри олимпиады в соответствии с особенностями решений школьников данной школы. Каждая задача оценивается целым числом баллов от 0 до 7. Итог подводится по сумме баллов, набранных участником.
Основные принципы оценивания задач :
7 баллов — Полное верное решение.
6-7 баллов Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение
5-6 баллов Решение в целом верное. Однако оно содержит ряд ошибок, либо не рассмотрение отдельных случаев, но может стать правильным после небольших исправлений или дополнений.
4 балла Верно рассмотрен один из двух (более сложный) существенных случаев.
2-3 балла Доказаны вспомогательные утверждения, помогающие в решении задачи.
1 балл Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).
0 баллов Решение неверное, продвижения отсутствуют.
0 баллов Решение отсутствует.
Олимпиадная работа не является контрольной работой участника, поэтому любые исправления в работе, в том числе зачеркивание ранее написанного текста, не являются основанием для снятия баллов; недопустимо снятие баллов в работе за неаккуратность записи решений при ее выполнении. Баллы не выставляются «за старание участника», в том числе за запись в работе большого по объему текста, но не содержащего продвижений в решении задачи. Победителем в параллели считается участник, набравший наибольший суммарный балл и решивший не менее половины задач (не менее трех задач). Победителей в параллели может быть несколько. Призерами рекомендуется считать участников, решивших не менее половины задач, но набравших меньше баллов, чем победитель. Если ни один участник в данной параллели не решил более двух задач, жюри может принять решение считать призерами участников, решивших две задачи, однако победителей в этом случае не будет.
ОТВЕТЫ
Решение задания №1.
Один из вариантов, не самый короткий, предусматривает использование 8 троек:
(33 — 3) : 3 · (33 — 3) : 3 = 100
Аналогично: (333 — 33) : 3 = 100.
Ответ №2: Малыш-3, Алиса-2, Кай-1, Женя-4 место.
Ответ№3: ? = 15, а общая площадь равна 75.
Решение задания №4.
Масса рыбы 12 кг. Г + Т = 10, Т + Х = 8, Г + Х = 6, 2( Г + Т + Х)= 24, Г + Т + Х =12.
Решение задания №5.
Пусть сыну сейчас x лет, отцу — 4x лет, тогда x+4x=50 . Сыну сейчас 10 лет, а через y лет будет 10+y лет, а отцу 40+y лет 3(10+y) = 40+y; y=5
Ответ: через 5 лет
Олимпиадные задачи по математике, 6 класс.
Олимпиадные задачи по математике, 6 класс.
1.На некотором острове необычайно регулярный климат: по понедельникам и средам идут дожди, по субботам – туман, зато в остальные дни – солнечно. Утром какого дня недели нужно начать свой отдых группе туристов, если они хотят пробыть там 44 дня и захватить при этом как можно больше солнечных дней? ( 3 балла )
А- в понедельник, В- в среду, С- в четверг, Д- в пятницу, Е – во вторник.
2.Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18. На какое число делили? ( 3 балла )
А – 18, В – 32, С – 24, Д – 36, Е – 48.
3.Если кенгуру научится прыгать в 1,5 раза дальше, чем умеет, ему понадобится ровно 6 прыжков, чтобы добраться до тенистого дерева. За сколько прыжков кенгуру может это сделать сейчас? ( 3 балла )
А – 3, В -4, С – 6, Д – 9, Е – невозможно определить.
4.На каждой кочке в маленьком болотце сидят не меньше, чем по 3 лягушки, а всего лягушек 145. Тогда число кочек в этом болотце не может равняться: ( 3 балла )
А – 1, В – 23, С – 31, Д – 44, Е – 55.
5.Выполните действия рациональным способом
354 * 73 + 23 *25 + 354 * 27 +17 * 25 ; ( 5 баллов )
6.На одной чашке весов лежат шесть одинаковых пачек чая и гиря массой 50 г, а на другой – одна пачка чая и две гири массой 100 г и 200 г. Весы находятся в равновесии. Определите, сколько граммов весит одна пачка чая? ( 6 баллов )
7.Из 40 учащихся 6 класса 32 ходят на кружок «Умелые руки», 21 посещают спортивную секцию, 15 учащихся ходят и на кружок и на секцию. Сколько учащихся не ходят на этот кружок, ни на эту секцию? ( 6 баллов )
Ответы. 1.- С; 2.- С; 3.- Д; 4.- Е; 5.-36400; 6.-50 г; 7.- 2 уч.
Олимпиадные задачи по математике, 6 класс, 2 тур.
1.Гусеница ползёт по стволу яблони. За первый час она поднялась на 10 см, за второй час опустилась на 4 см, за третий час вновь поднялась на 10см, а за четвёртый опустилась на 4 см. Так она продолжала подниматься и опускаться в течение нескольких часов. На сколько сантиметров поднимется гусеница за 11 ч? (5 баллов)
2.Решите уравнение |2x|*|-3,5|=|-28|. (3 балла)
3.В детский летний лагерь приехали три друга: Миша, Володя, Петя. Известно. Что каждый из них имеет одну из фамилий: Иванов, Семёнов, Герасимов. Миша не Герасимов. Отец Володи инженер. Володя учится в 6 классе. Ребёнок с фамилией Герасимов учится в 5 классе. Отец с фамилией Иванов – слесарь. Какая фамилия у каждого из друзей? (4 балла)
4.Запиши число 100 девятью различными цифрами, соединёнными знаками действий. (4 балла)
5.У фермера было несколько одинакового веса поросят и несколько ягнят также одинакового веса. Мальчик спросил фермера, сколько весит один поросёнок и один ягнёнок. Фермер ответил, что 3 поросёнка и 2 ягнёнка весят 22 кг, а 2 поросёнка и 3 ягнёнка весят 23 кг. Как узнать, сколько весит один поросёнок и сколько весит один ягнёнок? (5 баллов)