Сборник олимпиадных задач по математике 5-6 классов
Подготовка к олимпиадам
Сборник х задач для учащихся 5-6 классов
Введение
Если бы спросить всех школьников, какой предмет нравится им больше других, то вряд ли большинство из них назовет математику. Обычно ее скорее уважают, чем любят.
Математика — одна из самых древних и важных наук. Многими математическими знаниями люди пользовались еще в глубокой древности – тысячи лет назад. И в наши дни ни одному человеку не обойтись в жизни без хорошего знания математики. Основа хорошего понимания математики — умение считать, думать, рассуждать, находить удачные решения задач. Все эти навыки и способности можно выработать, если быть настойчивым, трудолюбивым и внимательным на уроках, быть самостоятельным и с интересом заниматься дома. А вот решение олимпиадных задач существенно отличается от решения школьных, даже очень сложных, задач!
Олимпиадные задачи, как правило, являются нестандартными, т.е. требующими использования всех знаний в нестандартных ситуациях, но в школьном курсе математики этому вопросу внимания практически не уделяется. Не смотря на это, роль олимпиад становится все более значимой. Многочисленные олимпиады дают их победителям и призёрам право поступления в высшие учебные заведения. При сдаче ЕГЭ по математике в некоторых заданиях, предлагаются олимпиадные задачи.
Актуальность решения олимпиадных задач заключается в предоставлении учащимся ещё одной возможности поступить по результатам олимпиад, повысить уровень математической грамотности, даёт шанс стать победителем!
Чем раньше начать подготовку к участию в различных олимпиадах, тем больше шансов стать победителем.
Краткая характеристика олимпиад по математике.
Математические олимпиады школьников являются одной из важных форм внеклассной работы по предмету. Они не только помогают выявить одаренных, способных учащихся, но и стимулируют углубленное изучение предмета, служат развитию интереса к математической науке. Кроме того, олимпиады способствуют созданию необходимых условий для поддержки одаренных, способных детей.
Прообразом первой математической олимпиады было Этвешское соревнование, которое проводилось в Венгрии в 1986 году. А вот в Москве олимпиады по математике проводиться стали с 1935 года и возраст участников был 16-20лет. В последние годы в России стало проводиться много различных математических олимпиад.
Структура математических олимпиад
Основными целями и задачами математических олимпиад являются:
— пропаганда научных знаний и развитие у обучающихся интереса к научной деятельности;
— создание необходимых условий для выявления одаренных детей;
— организация работы факультативных занятий, кружков.
Привлекательными являются условия нестандартных задач, предлагаемых на олимпиадах, заметно отличающиеся от обязательных, при изучении школьного материала заданий, направленных на отработку выполнения стандартных алгоритмов. Олимпиадные задачи, как правило, это задачи повышенной сложности, нестандартные как по формулировке, так и по методу решения. Среди них встречаются и особенные задачи, в решении которых требуются специальные методы и необычные идеи, а более стандартные задачи могут быть решены оригинальным методом.
Особенности олимпиадных задач
Олимпиадная математика школьников развивает математическое мышление, повышает качество общей математической подготовки, создает базу для успешного выступления учащихся на математических олимпиадах и конкурсах различного уровня.
Олимпиадные задачи по математике 5 класса из разных источников.
Олимпиадные задачи школьного этапа Всероссийской олимпиады школьников в городе Саров.
2018-2019 учебный год.
Задача:
Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо
сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки.
Без Мышки все остальные не могут вытащить репку, а вместе с Мышкой – могут.
Сколько мышек надо собрать вместе, чтобы эти мышки смогли вытащить репку
сами?
Решение:
Кошка = 6 мышек; жучка = 5 кошек = 30 мышек; внучка = 4 жучки = 120
мышек; бабка = 3 внучки = 360 мышек; дедка = 2 бабки = 720 мышек. Все вместе
дедка + бабка + внучка + жучка + кошка + мышка =
= 720+360+120+30+6+1=1237 мышек.
2017-2018 учебный год.
5.1. Замените буквы цифрами так, чтобы все равенства стали верными:
А . Р = И – Ф = М : Е = Т – И = К : А . Одинаковым буквам соответствуют одинаковые цифры, разным буквам – разные цифры.
Решение: 2.1=7-5=6:3=9-7=4:2
А-2;Р-1;К-4;И-7;Ф-5;Т-9;М-6;Е-3.
5.2. В прошлом году в школьной математической олимпиаде участвовали 58 пятиклассников. Сумма их возрастов составляла 641 год. А чему будет равна сумма их возрастов ровно через два года?
Решение: Возраст каждого из учеников увеличится на 2. Значит, сумма возрастов вырастет на 58.2=116 лет. Поэтому вместе им будет 641+116=757 лет
5.3. Вася и Петя, поссорившись, разбежались с одинаковыми скоростями в противоположных направлениях. Через 5 минут Вася спохватился, повернул назад, и, увеличив скорость, побежал догонять Петю. Во сколько раз увеличил скорость Вася, если он догнал Петю через 5 минут после того как повернул назад?
Решение:

Пусть О – место ссоры, В и Р точки, в которых соответственно находились Вася и Петя через 5 минут после ссоры.
За следующие 5 минут Петя пробежал расстояние равное ОР и оказался в точке К. Значит, Вася должен был за это же время пробежать расстояние ВК, которое в три раза больше, чем РК. Следовательно, его скорость должна быть в три раза больше, чем у Пети.
2016-2017 учебный год.
5.1. На уроке физкультуры мальчики построились в шеренгу. Потом между каждыми двумя мальчиками встала девочка. Всего в шеренге оказалось 25 детей. Сколько мальчиков стояло в шеренге?
Решение: Уберем самого правого мальчика. Тогда мальчиков и девочек будет поровну, то есть по 12. Значит, в шеренге стояло 12+1=13 мальчиков.
5.2. Может ли быть верным равенство К·О·Т = У·Ч·Е·Н·Ы·Й, если в него вместо букв подставить цифры от 1 до 9? Разным буквам соответствуют разные цифры. Ответ обоснуйте.
Решение: Одной из букв обязательно должна соответствовать цифра 7 и тогда та часть равенства, в которую входит эта буква, будет делиться на 7, а другая – не будет.
5.3. Из 16 одинаковых квадратов со стороной 1 см сложите прямоугольник:
а) наибольшего периметра; б) наибольшей площади. Ответ обоснуйте.
Решение:
а) Прямоугольник 1×16 имеет наибольший периметр, равный 34 см. б) Любой прямоугольник, сложенный из 16 квадратов, имеет площадь 16 см2.
5.4. Из Простоквашино в Печкино на лыжах вышли Шарик и Матроскин. Шарик дошел до Печкино за 30 минут, развернулся, и через 5 минут на обратном пути встретил отстающего Матроскина. Сколько минут после этого Шарик должен идти по направлению к Простоквашино, чтобы, развернувшись обратно, он пришёл в Печкино одновременно с Матроскиным?
Решение: Путь от Простоквашино до места встречи, который Матроскин проделал за 30+5=35 минут, Шарик проделал за 30-5=25 минут. Следовательно, путь от места встречи до Печкино, который Шарик проделал за 5 минут, в 5 раз меньше пути от от Простоквашино до места встречи. Поэтому Матроскин проделает путь от места встречи до Печкино за 7 минут. Значит, Шарику остаются 2 минуты, и он должен поделить их поровну между дорогой от места встречи в сторону Простоквашино, и обратной дорогой до места встречи.
5.5. Разбейте данный квадрат по сторонам клеток так, чтобы все части были одинакового размера и формы, чтобы каждая содержала по одному кружку и звездочке.

2015-2016 учебный год.
5.1. Парусник отправляется в плавание в понедельник в полдень. Плавание будет продолжаться 100 часов. Назовите день и час его возвращения в порт.
Решение: В сутках 24 часа, поэтому 100 ч. = 4×24 ч. + 4 ч. = 4 сут. + 4 ч.. Тогда, парусник вернётся в пятницу в 16 часов.
5.2. Возраст старика Хоттабыча записывается числом с различными цифрами. Об этом числе известно следующее:
— если первую и последнюю цифры зачеркнуть, то получится двузначное число, которое при сумме цифр, равной 13, является наибольшим;
— первая цифра больше последней в 4 раза. Сколько лет старику Хоттабычу?
Решение: Так как после зачёркивания получается наибольшее число с суммой цифр 13, то вторая и третья цифры равны 9 и 4. Так как первая цифра больше последней в 4 раза и все цифры различны, то первая цифра будет 8, а последняя – 2. В результате получилось число 8942. старику Хоттабычу 8942 года.
5.3. Разгадайте ребус, в котором одинаковые цифры обозначены одинаковыми буквами, а разные цифры разными буквами: УДАР + УДАР = ДРАКА.
Решение: Из разрядов сотен видно, что А=2, или А=3, но из разрядов единиц видно, что А-четно, значит, А=2. Из разрядов единиц Р=1 или Р=6, но Д=1, значит, Р=6. У и К находятся просто У+У=16, К=2+2.
Ответ. 8126+8126=16252.
5.4. Двузначное число при делении на 2 даёт остаток 1, при делении на 3 – остаток 2, при делении на 4 – остаток 3, при делении на 5 – остаток 4. Что это за число?
Решение: Прибавив к искомому числу единицу, мы получим число, делящееся без остатка и на 2, и на 3, и на 4, и на 5, то есть число, делящееся на 60. Это могут быть числа 60,120,180 и т.д. Значит, задуманное число 59.
5.5. На сколько частей могут разделить треугольник три пересекающие его прямые?
Решение: На 4, на 5, на 6 или на 7 частей.
Олимпиадные задачи по математике 6 класса из разных источников.
Олимпиадные задачи школьного этапа Всероссийской олимпиады школьников в городе Саров.
2018-2019 учебный год
Задача:
Мышь, мышонок и сыр вместе весят 180г. Мышь весит на 100г больше, чем
мышонок и сыр вместе взятые. Сыр весит в три раза меньше, чем мышонок. Сколько
весит каждый из них? Ответ нужно подтвердить вычислениями.
Решение:
Мышь-140г, сыр-10г, мышонок-30г
Из условия следует, что удвоенный вес мыши 180+100=280г. Поэтому вес мыши равен
140г. Тогда мышонок и мышь вместе весят 180-140=40г. А вес сыра, согласно
условию, в 4 раза меньше, т.е. 10г.
2017-2018 учебный год
Задача:
Арбуз весил 20 кг и содержал 99% воды, когда он немного усох, то стал
содержать 98% воды. Сколько теперь весит арбуз?
Решение:
Вес «сухого вещества» в арбузе составляет 100 — 99 = 1 (%) или
0,01, т. е. 200,01 =0,2 (кг).
После «усыхания» арбуза вес «сухого вещества» составляет 100 — 98 = 2 (%) или
0,2 : 0,02 = 10 (кг).
Ответ: 10 кг.
2016-2017 учебный год
Задача:
Однажды в вагоне Таня стала зашифровывать слова, заменяя буквы их
номерами в алфавите. Когда она зашифровала пункты прибытия и
отправления поезда, то с удивлением обнаружила, что они записываются с
помощью лишь двух цифр 211221 – 21221. Откуда и куда идёт поезд?
Решение:
2 – Б; 1 – А; 12 – К; 21 – У;
21 – У; 22 – Ф; 1 – А.
Ответ. БАКУ – УФА.
2015-2016 учебный год
Задача:
Девочка по чётным числам всегда говорит правду, а по нечётным всегда врет. Как-то её три сентябрьских дня подряд спрашивали: «Как тебя зовут?». На первый день она ответила: «Ольга», на второй: «Лена», на третий: «Маша». Как зовут девочку? Объясните, как вы рассуждали.
Решение:
Девочку зовут – Лена.
Так как девочка дала три разных ответа, она хотя бы два раза соврала. Поэтому два дня из трех, когда девочке задавали вопросы, пришлись на нечётные числа. Поскольку чётные и нечётные числа чередуются, это должны были быть первый и третий дни. Значит, второй день пришёлся на чётное число. В этот день девочка и назвала своё настоящее имя.
Олимпиадные задачи на страницах учебников математики 5-6 классов.
Математика. 5 класс: учеб.для общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд.
Интеллектуальные задачи в данном учебнике обозначаются так:

№ 596. Сумма пяти натуральных чисел равна произведению этих чисел. Какие это числа?
Решение: 1+1+2+2+2+2=1×1×2×2×2=8
№ 865. Представьте себе, что один куб с ребром 1 дм разрезали на кубики с ребром 1 см и из этих маленьких кубиков сложили башню, поставив их один на другой. Второй куб с ребром 1 дм разрезали на кубики с ребром 1 мм и из этих кубиков так же сложили башню. Какая из этих башен выше? Во сколько раз?
Решение: Куб с а= 1дм
V= а³=1дм=1000см³=1000000мм³
Высота башни из кубиков с а=1 см равна 1×1000000=1000000мм
1000000:10000=100 раз, вторая башня выше первой.
1 случай: 1000 кубиков=высота башни 1000см=10м
2 случай: 1000000 кубиков=высота башни 1000000мм=1000м
1000:10=100 (раз) вторая выше
№ 1132. Пошёл дождь. Под водосточную трубу поставили пустую бочку. В неё вливалось каждую минуту 8 л воды, а через щель в бочке выливалось 3 л воды в минуту. Сколько литров воды будет в бочке через 1 мин; 2 мин; 3 мин? Успеет ли бочка наполниться, если её объём 400 л, а дождь шёл 1 ч 10 мин?
Решение: 1) 8-3=5 (л)-в бочке через 1 мин.
2) 5×2=10 (л)-через 2 мин.
3) 5×3=15 (л)-через 3 мин.
4) 5×70=350 (л)-через 1ч 10мин
350л < 400л. Ответ: Бочка не успеет наполниться.
Математика. 5 класс. 1,2 часть-Г.В. Дорофеева, Л.Г.Петерсон.
Данный учебник содержит в каждом параграфе задачи на смекалку, для них характерно следующее обозначение:

№ 714 (часть 1). Может ли быть верным равенство: К×О×Т=У×Ч×Ё×Н×Ы×Й. Если в него вместо букв поставить цифры от 1 до 9 (разным буквам соответствуют разные цифры)?
Решение: Равенство неверное т.к. в него входят все цифры от 1 до 9 по одному разу. Это значит, что в одну из частей входит цифра 7, а в другую нет т.е. одна из частей делится на 7, а другая нет.
№820 (часть 1). Спросил некто учителя: сколько у тебя в классе учеников, так как хочу дать к тебе в учение своего сына? Учитель ответил: если придёт ещё учеников столько же, сколько имею, и полстолько и четвёртая часть и твой сын, тогда будет у меня учеников 100. Спрашивается: сколько было у учителя учеников?
Решение:
Первый способ.
Пусть х учеников – у учителя.
х + х + х/2 + х/4 + 1=100
х + х + х/2 + х/4=99
х × 4+4+2+1/4=99
х × 11/4=99
х=99:11/4=99×4/11=36 (учеников) Второй способ.
Пусть х четвёртая часть 2х-полстолько, 4х-столько
4х+4х+2х+х+1=100
11х=99
х=9
4х=36 (учеников)
№ 183 (часть 2). В сказочной стране Перра-Терра среди прочих обитателей проживают Карабасы и Барабасы. Каждый Карабас знаком с девятью Барабасами, а каждый Барабас знаком с десятью Карабасами. Кого в этой стране больше-Карабасов или Барабасов?
Решение: Карабасов больше, т.к. их минимальное кол-во 10, а Барабасов-9.
Математика: 5 класс: учебник для учащихся общеобразовательных организаций/ А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
В данном учебнике каждый параграф заканчивается особой задачей, которую авторы назвали «Задачи от мудрой совы».

№ 43. В этом году день рождения отца был в воскресенье. В какой день недели праздновала свой день рождения мать, если она на 62 дня моложе отца?
Решение: Поскольку мать младше отца, то 62 дня надо прибавить к дате дня рождения отца. Дни. Номера которых делятся нацело на 7, будут приходиться на воскресенье. Следовательно, шестьдесят второй день-суббота.
№ 358. Каждый учащийся гимназии изучает по крайне мере один из двух иностранных языков. Английский язык изучают 328 учеников, французский язык-246 учеников, а английский и французский одновременно -109 учеников. Сколько всего учеников учится в гимназии?
Решение: В гимназии 328+246-109=465 (учеников).
№ 757. В коробке лежало 4 белых, 5 чёрных и 6 красных шариков. Какое наименьшее количество шариков надо вынуть из коробки, чтобы среди них обязательно оказались:
1) 3 шарика одного цвета; 2) шарики всех трёх цветов?
Решение: 1) Семь шариков. Шести шариков недостаточно. В этом случае может оказаться, что вынули по два шарика каждого из трёх цветов.
2) Двенадцать шариков. Если вынуть только 11 шариков, то возможен будет такой вариант: 5 чёрных и 6 красных.
№ 1091. Как поделить поровну 7 яблок между 12 друзьями, если каждое яблоко можно разрезать не более чем на 4 части?
Решение: Четыре из семи яблок надо разделить на 3 равные части каждое, а три оставшихся яблока — на 4 равные части каждое.
Математика. 6 класс: учеб.для общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд.
Интеллектуальные задачи в данном учебнике обозначаются так:

Задача:

Решение:
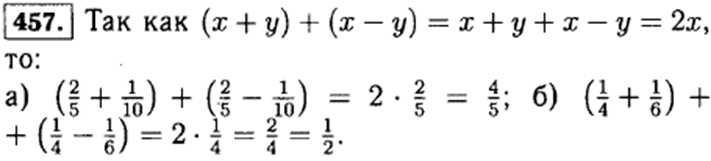
Математика. 6 класс. 1,2 часть-Г.В. Дорофеева, Л.Г.Петерсон.
Данный учебник содержит в каждом параграфе задачи на смекалку, для них характерно следующее обозначение:

Задача:

Решение:

Математика: 6 класс: учебник для учащихся общеобразовательных организаций/ А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
В данном учебнике каждый параграф заканчивается особой задачей, которую авторы назвали «Задачи от мудрой совы».

Задача:

Решение:
За 7 стирок все стороны (высота ,ширина и длинна) уменьшились вдвое, а объем его уменьшается в 8 раз.
Допустим весь кусок разделили на 8 равных частей, а после 7 стирок он уменьшился на 7/8 (за 1 стирку уменьшался на 1 часть)
Осталось 1/8=то есть оставшегося куска мыла хватит на одну стирку
Задачи из дистанционных олимпиад.
В этом году я принимала участия во многих дистанционных олимпиадах по математике на сайтах: МетаШкола, Фоксфорд, Uchi.Ru, Prodlenka.
Наиболее интересные задачи представлены ниже:
МетаШкола:
Задача: В темной комнате в коробке лежали 5 зелёных и 6 синих карандаша. Сколько нужно достать карандашей, чтобы убедиться, что попался хотя бы один зелёный карандаш?
Решение: нужно взять 7 карандашей, тогда у нас будет 6 синих и один зелёный.
Фоксфорд:
Задача: Буратино купил папе Карло куртку. Если к стоимости куртки прибавить сумму, которая была у Буратино изначально, и сумму, которая осталась после покупки, то получится 12 сольдо. Сколько сольдо было у Буратино изначально?
Решение: Пусть x сольдо было у Буратино изначально, y — стоимость куртки, (x-y) — столько сольдо осталось после покупки куртки
Составим уравнение по условию задачи y+x+(x-y) = 12
2x=12
x=6
Ответ: 6 сольдо было у Буратино изначально.
Uchi.Ru:
Задача: Аня съедает 900г. варенья за 9 минут. Лёша делает это вдвое быстрее. За сколько минут они вместе съедят 1кг 800г. варенья?
Решение: 1) 900:9= 100 (гр)- Аня съедает за минуту
2) 100×2=200 (гр) – съедает за минуту Леша.
Вместе за минуту они съедят 300(гр)
1800:300=6 за 6 минут
Prodlenka:
Задача: Лестничный марш содержит 9 ступенек высотой по 0,18 м каждая. Между соседними этажами здания два лестничных марша. На какую примерно высоту поднялась кошка, если она бежала с первого этажа до пятого? Ответ округлен до метров.
Решение: 1) 9×2=18 -столько ступенек бежала кошка
2) 18×0,18=3,24м -высота всех ступенек на одном этаже
3)с первого по 5 этажи всего четыре пролета
значит 3,24×4=12,96м≈13 м.
Полезные советы самоподготовки к олимпиаде по математике.
1. Тщательно ознакомьтесь с заданиями, которые были на олимпиаде в прошлом году. Если вы участвовали в ней, вспомните свои ошибки, решите эти задания еще раз, разберитесь, почему вы были не правы. Добейтесь понимания своих ошибок и прочитайте дополнительный материал по сложным для вас темам не только в учебнике, но и в энциклопедиях или книгах для углубленного изучения.
2. Пролистайте свой учебник по математике, чтобы освежить в памяти список тем, которые будут освещены заданиями на олимпиаде. Выпишите на отдельный листок основные формулы и всю базовую математическую информацию, которая дает ключ к решению задач.
3. Порешайте задания отмеченные звездочкой. Они являются немного более сложными по сравнению с остальными, зато обычные однотипные задачи вы будете после этого решать гораздо легче.
4. Решите несколько особых «заданий на логику», которые развивают мышление. Это позволит вам при решении математических задач лучше понять их суть, логичнее рассуждать и быстрее прийти к правильному ответу.
5. Составьте список вопросов, ответы на которые вам так и не удалось получить самостоятельно. Занесите в этот список сложные и непонятные для вас темы.
6. Попросите вашего преподавателя по математике об индивидуальном занятии после уроков. Учитель, заинтересованный в победах своих учеников, обязательно уделит вам время. Задайте все вопросы из составленного списка, расскажите учителю о всех трудностях, которые возникли у вас во время самостоятельной работы с учебниками. Возможно, кроме объяснений, преподаватель даст вам несколько дополнительных полезных советов.
Олимпиадные задания по математике (5, 6 класс) по теме: Школьный этап Всероссийской Олимпиады по математике в 5 и 6 классах
Задания школьного этапа Всероссийской олимпиады школьников
Шестой класс
1.В записи (88888888) нужно поставить знаки сложения таким образом, чтобы получилась сумма, которая будет равна 1000.
2. Малыш, Алиса, Кай и Женя заняли первые четыре места в соревнованиях, причем никто из них не делил между собой какие-нибудь места. Известно:
- Малыш не был ни первым, ни четвертым.
- Алиса заняла второе место.
- Кай не был последним.
Какое место занял каждый?
3. Мама дала Зое денег ,чтобы она в школьном буфете купила завтрак.
Когда Зоя вер вернулась из школы, то перед мамой отчиталась так: «1/2 всех денег я истратила на бумагу,1/5 -на чай, а 3/10 -на конфеты». Мама догадалась, что дочь истратила все деньги. Как она узнала ?
4. «Змей Горыныч побежден!»-такая молва дошла до Микулы Селяниновича. Он знал, что мог это сделать либо Илья Муромец, либо Алеша Попович, либо Добрыня Никитич. Вскоре Микуле сообщили:
1)Змея Горыныча победил не Илья Муромец;
2)Змея Горыныча победил Алеша Попович.
Спустя некоторое время выяснилось, что одно их этих сообщений неверное, а другое верное. Догадайтесь, кто из трех богатырей победил Змея Горыныча.
5.Трое рыбаков поймали 75 карасей. Стали варить уху. Когда один дал 8 карасей, а другой 12, а третий-7, то карасей у них стало поровну. Сколько карасей поймал каждый рыбак?
6. Имеется 8 палочек длиной в 1см, 8 палочек длиной в 2см и 7 палочек длиной в 5 см.
Можно ли из всех палочек этого набора сложить прямоугольник?
Разламывать палочки нельзя.
.
О Т В Е Т Ы И РЕШЕНИЯ
ШКОЛЬНОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
6 класс
1. (6 баллов) В записи (88888888) нужно поставить знаки сложения таким образом, чтобы получилась сумма, которая будет равна 1000.
Решение:
Способ 1: 88+8+8+8+888=1000
Способ 2: 8+8+888+88+8=1000.
2. (6 баллов) Малыш, Алиса, Кай и Женя заняли первые четыре места в соревнованиях, причем никто из них не делил между собой какие-нибудь места. Известно:
- Малыш не был ни первым, ни четвертым.
- Алиса заняла второе место.
- Кай не был последним.
Какое место занял каждый?
Ответ: Малыш-3, Алиса-2, Кай-1, Женя-4 место.
3. (6 баллов) Мама дала Зое денег ,чтобы она в школьном буфете купила завтрак. Когда Зоя вер вернулась из школы, то перед мамой отчиталась так: «1/2 всех денег я истратила на бумагу,1/5 -на чай, а 3/10 -на конфеты». Мама догадалась, что дочь истратила все деньги. Как она узнала?
Решение: 1/2+1/5+3/10=1, т.е. все деньги
4. (6 баллов) «Змей Горыныч побежден!»-такая молва дошла до Микулы Селяниновича. Он знал, что мог это сделать либо Илья Муромец, либо Алеша Попович, либо Добрыня Никитич. Вскоре Микуле сообщили:
1)Змея Горыныча победил не Илья Муромец;
2)Змея Горыныча победил Алеша Попович. Спустя некоторое время выяснилось, что одно их этих сообщений неверное, а другое верное. Догадайтесь, кто из трех богатырей победил Змея Горыныча.
Ответ. Добрыня Никитич.
Решение. Предположим, что Змея Горыныча победил Илья Муромец. Тогда оба сообщения неверные-результат не соответствует условию задачи. Предположим, что Змея Горыныча победил Алеша Попович.Тогда оба сообщения верные. И этот результат не соответствует условию задачи.
Предположим, что Змея Горыныча победил Добрыня Никитич.Тогда первое сообщение верное, а второе- неверное. Результат соответствует условию задачи
5. (6 баллов) Трое рыбаков поймали 75 карасей. Стали варить уху. Когда один дал 8 карасей , а другой 12, а третий-7, то карасей у них стало поровну. Сколько карасей поймал каждый рыбак?
Решение. 75-8-12-7=48(осталось всего окуней)
48 окуней на 3 рыбака.48:3=16
У каждого рыбака осталось по 16 окуней
16+ 8 = 24 — поймал 1 рыбак
16 + 12 = 28 — поймал 2 рыбак
16 + 7 = 23 — поймал 3 рыбак
Ответ: 24, 28, 23.
6. (6 баллов) Имеется 8 палочек длиной в 1см, 8 палочек длиной в 2см и 7 палочек длиной в 5 см. Можно ли из всех палочек этого набора сложить прямоугольник? Разламывать палочки нельзя.
Решение.
Если a и b – длины сторон прямоугольника, периметр P = 2(a+b), т. е. P – четное число в случае целых a и b.
8*1+8*2+7*5=8+16+35=59 (см) – нечетное число.
Поэтому из всех палочек данного набора прямоугольник сложить нельзя.
Ответ: нельзя
Муниципальная олимпиада по математике 5-6 класс
Олимпиада муниципального уровня.
Олимпиада по математике для учащихся 5 класса
Найдите цифры, вместо которых стоят звездочки: (5 баллов)
* 8 *
4 * 2
——-
7 * 0
* * *
* * * *
—————
* * * * 2 *
На одной чаше весов лежат шесть одинаковых пачек чая и гиря массой 50г., а на другой – одна пачка чая и две гири массой 100 и 200 г. Весы находятся в равновесии. Определите, сколько граммов весит одна пачка чая? (5 баллов)
Определите недостающую фигуру и нарисуйте на чистовике: (6 баллов)

В олимпийской команде по конному спорту пять голов и четырнадцать ног. Сколько из них людей, а сколько лошадей? (6 баллов)
Клоуны БАМ, БИМ и БОМ вышли на арену в красной, синей и зелёной рубашках. Их туфли тоже были тех же разных цветов. Туфли и рубашка БИМА были одного цвета. На БОМЕ не было ничего красного. Туфли БАМА были зелёными, а рубашка – нет. Каких цветов были туфли и рубашка у БОМА и БИМА? (7 баллов)
Когда у рыбака спросили, как велика пойманная им щука он сказал: « Я думаю, что хвост её – 1 кг, голова – столько, сколько хвост и половина туловища, а туловище – сколько голова и хвост вместе. Сколько весит щука? (7 баллов)
Ответы и решения олимпиады по математике 5 класс
Указание: Усмотреть, что последняя цифра в первом числе – это 0 или 5, а первая цифра – 3, а затем перебрать несколько вариантов.
Ответ: 385·412=158620.Решение: 1)100+200=300 грамм на одних весах.
2)300-50=250 грамм чая
3)250:(6-1)=50
Ответ: 50 г.Указание: оценить задание на 6 баллов
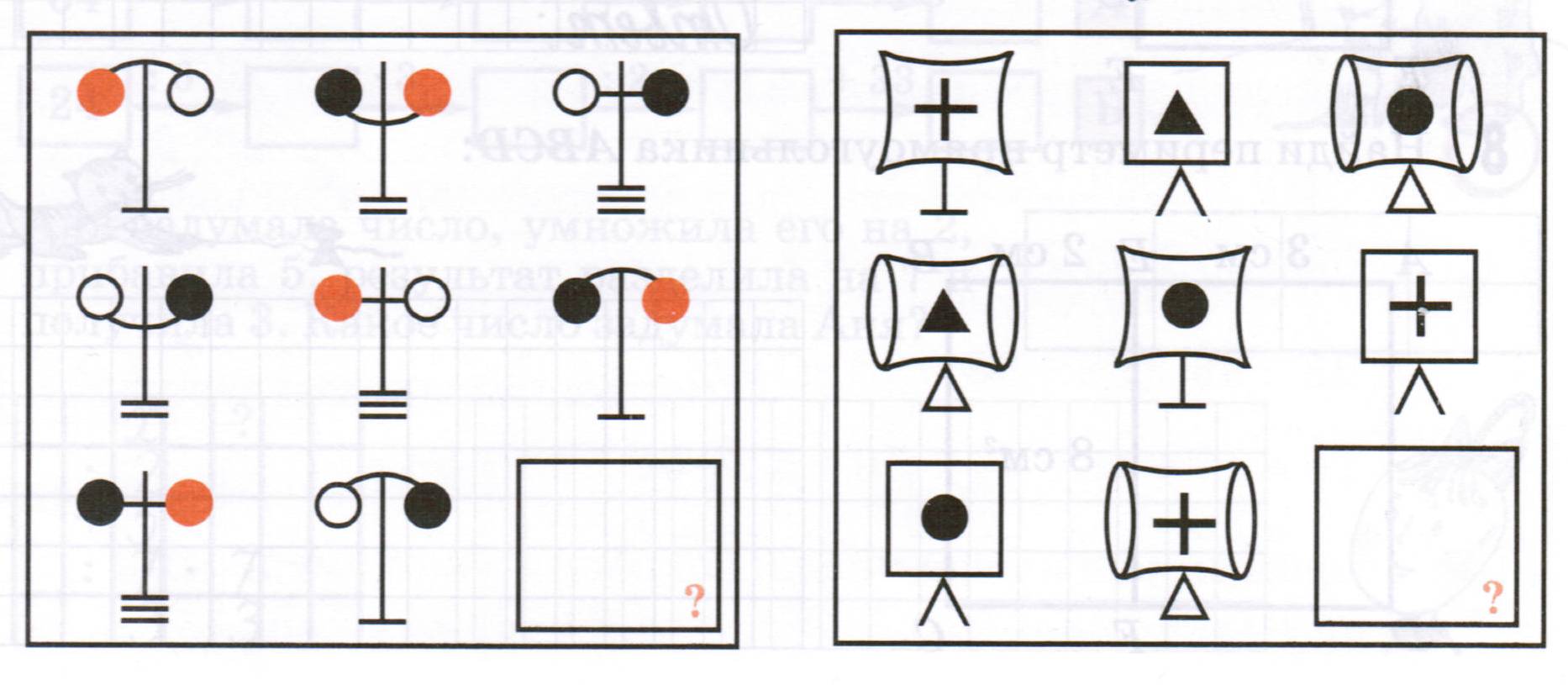
Ответ. 3 человека и 2 лошади.
Решение. Предположим сначала, что все пятеро – люди. Это 5 голов и 10 ног. Замена одного человека на лошадь дает +2 ноги. У нас пока что недостает 4 ноги. Значит, нужно 2 человека заменить лошадьми.
5.Решение:
На Баме были зелёные туфли, а на Боме туфли не могли быть зелёными и не могли быть красными. Значит, на Боме туфли синие, поэтому на Биме туфли, а потом и рубашка красные. На Баме рубашка синего цвета, а на Боме – зелёного.
Ответ: туфли Бома – синие туфли Бима – красные, рубашка Бима – красная , а рубашка Бома – зелёная.
6. Решение:
Пусть 2х кг весит туловище щуки, тогда голова будет весить (х+1) кг. Из условия, что туловище весит столько же, сколько голова и хвост вместе получим уравнение: 2х = х + 1 + 1. Откуда х = 2, а вся щука будет весить 8 кг.
Ответ: щука весит 8 кг.
Основные принципы оценивания приведены в таблице.
в целом верно и может стать полностью правильным после небольших
исправлений или дополнений.
4
Верно рассмотрен один из двух (более сложный) существенных случаев.
2-3
Доказаны вспомогательные утверждения, помогающие в решении задачи.
1
Рассмотрены отдельные важные случаи при отсутствии решения (или при
ошибочном решении).
0
Решение неверное, продвижения отсутствуют.
0
Решение отсутствует.
Олимпиада по математике для 6 класса
1. Вычислите : (5 баллов)
.
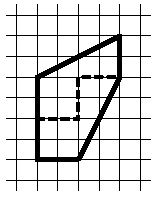
2. Разрежьте изображённый на рисунке пятиугольник на две одинаковые (совпадающие при наложении) части. (5 баллов)
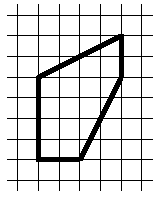
3. Пять спортсменов: футболист, велосипедист, пловец, гимнаст и боксёр, из разных стран: Германии, Франции, Италии, Украины и России встретились на Олимпийских играх.
Спортсмены из Франции и Украины никогда не играли в футбол. Спортсмены из Германии и Украины не любят ездить на велосипеде. Француз и немец обменялись адресами с гимнастом. Немец и итальянец посетили выступления пловца и футболиста. Велосипедист не француз.
Определите какой спортсмен из какой страны. (6 баллов)
4. В ряд выписано 12 девяток 999999999999. Поставьте между ними знаки:
+ , — , : , . , скобки, так чтобы получилось 2014 – год Олимпийских игр в Сочи. (6 баллов)
5. Три купчихи — Сосипатра Титовна, Олимпиада Карповна и Поликсена Уваровна — сели пить чай. Олимпиада Карповна и Сосипатра Титовна выпили вдвоём 11 чашек, Поликсена Уваровна и Олимпиада Карповна — 15, а Сосипатра Титовна и Поликсена Уваровна — 14. Сколько чашек чая выпили все три купчихи вместе? (7 баллов)
6. В рисе содержится 75% крахмала, а в ячмене – 60%. Сколько надо взять ячменя, чтобы в нем содержалось бы столько крахмала, сколько его содержится в 9 кг риса? (7 баллов)
Ответы и решения олимпиады по математике 6 класс
1. =
==111111.111111-111111.111111=0.
2. Ответ 
3. Решим задачу с помощью таблицы.
Ответ: футболист из Росии, велосипедист из Италии, пловец из Франции, гимнаст из Украины, боксёр из Германии.
4. Возможны варианты:
а) 999 + 999 + 9 + 9 — 9 : 9 — 9 : 9 .
5. Ответ: 20 чашек
Решение:
СТ+ОК=11 — по условию задачи
ПУ+ОК=15 — по условию задачи
СТ+ПУ+2ОК=26,
СТ+ПУ=14- по условию задачи
14+2ОК=26
2ОК=12
ОК=6
СТ=5
ПУ=9
ОК+СТ+ПУ=20
6.
9 . 0,75 = 6,75(кг)- содержится крахмала в 9 кг риса;
6,75 : 0,6 = 11,25(кг) – надо взять ячменя.
Основные принципы оценивания приведены в таблице.
в целом верно и может стать полностью правильным после небольших
исправлений или дополнений.
4
Верно рассмотрен один из двух (более сложный) существенных случаев.
2-3
Доказаны вспомогательные утверждения, помогающие в решении задачи.
1
Рассмотрены отдельные важные случаи при отсутствии решения (или при
ошибочном решении).
0
Решение неверное, продвижения отсутствуют.
0
Решение отсутствует.
Олимпиадные задачи для 5-6 классов по математике
Олимпиадные задачи для 5-6 классов |
Шаманова Любовь Сергеевна |
Цели:1) повышение интереса к математике как к учебному предмету;
2) воспитание в будущих математиках таких качеств как творческий подход, нетривиальное мышление и умение изучить проблему с разных сторон.
Задачи: 1. Стимулирование продуктивной деятельности учащихся 5-6 классов, ориентированной на личностную и творческую самореализацию.
2.Задания олимпиады направлены на проверку внимания и логического мышления.
Задачи на переливание:
1) Имеются шестилитровая банка сока и две пустые банки: трех- и четырехлитровая. Как налить 1 литр сока в трехлитровую банку?
Банки
6 л
4 л
3 л
До переливания
6
0
0
После 1-го переливания
2
4
0
После 2-го переливания
2
1
3
После 3-го переливания
5
1
0
После 4-го переливания
5
0
1
2) Имеются два сосуда: один объемом 4 литра, а другой объемом 9 литров. Получится ли с их помощью налить из озера ровно 6 литров воды? Разрешается переливать всю воду из одного сосуда в другой и выливать воду из любого из них обратно в озеро.
3) Богатырь подошел к реке с двумя ведрами, вмещающими 15 литров и 16 литров. Удастся ли ему налить (отмерить) при помощи этих ведер ровно 8 литров воды?
4) Отлейте из бочки ровно 13 литра кваса при помощи двух бидонов: один емкостью 17 литров, а другой емкостью 5 литров.
5) Бочка вмещает 12 ведер воды. Для полива с вечера ее наполнили до верху. Имеются две пустые бочки, вмещающие 5 ведер и 8 ведер воды. Разлейте содержимое бочки поровну.
6) В канистре не менее 10 литров керосина. Можно ли отлить из нее 6 литров керосина, используя девятилитровую и пятилитровую канистру?
7) В бочке не менее 13 ведер воды. Можно ли из нее отлить ровно 8 ведер, если имеются две пустые бочки, вмещающие 9 и 5 ведер?
8) Имеется два полных бидона яблочного сока по 10 литров в каждом. Как налить из них в две пустые кастрюли объемами 4 литра и 5 литров по 2 литра молока?
9) Бидон емкостью 10 литров наполнен квасом. Требуется перелить из него 5 литров в семилитровый бидон, при помощи еще одного трехлитрового бидона. Как это сделать?
Задачи на города, дороги и графы
1) В шахматном турнире принимали участие 7 школьников. Известно, что Павел сыграл шесть партий, Марина – пять, Лена и Федя – по три Игорь и Денис — по две, Алиса – одну. С кем из участников турнира играла Лена?
Решение. Лучше проводить решение с помощью построения графа:
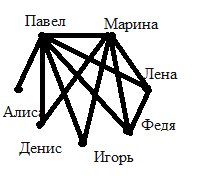 По построенному графу видно, что Лена играла с Мариной, Павлом и Федей.
По построенному графу видно, что Лена играла с Мариной, Павлом и Федей.
2) Победитель олимпиады по математике Антон отметил на доске 6 точек и соединил каждую из них ровно с четырьмя другими точками так, что все отрезки оказались непересекающимися. Вовочка случайно стер с доски все 6 точек. Сможете ли Вы повторить рисунок юного математика?.
3) Программистам компьютерного центра поставили задачу соединить имеющиеся 2013 компьютеров проводами так, чтобы каждый компьютер соединялся ровно с пятью другими. Смогут ли программисты осуществить этот план?
4) В стране «Цифрандия» построены девять городов с названиями 1,2,3,4,5,6,7,8,9. Путешествуя по стране, математик Антон заметил, что два города имеют железнодорожное сообщение в том случае, когда двузначное число, составленное из их цифр-названий, делится на 3. Можно ли поехать из города с названием 1 в город с названием 9?
5) Вовочка вернулся из путешествия по стране Врунляндия и рассказал учителю математики, что в ней есть озера и соединяющие их реки. Из каждого озера вытекают ровно 3 реки, но каждое озеро по 4 реки. Учитель математики без труда определил, что Вовочка сказал неправду. Как он до этого догадался?
6) Можно ли провести на листе бумаге 9 отрезков, чтобы каждый нарисованный отрезок пересекался ровно с тремя другими отрезками?
7) В сказочном новогоднем лесу 1000 деревьев, причем от каждого дерева отходит по 4 гирлянды к каким-то другим деревьям. Найдите количество гирлянд в этом лесу.
8) Репетитор по математике поставил ученику Диме задачу изобразить в тетради несколько точек и соединить их ровно 55-ю отрезками. Дима быстро нашел решение и оно оказалось правильным. Сколько точек он нарисовал репетитору по математике?
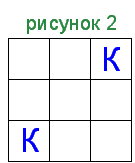
9) На миниатюрной шахматной доске расположены два коня, как показано на рисунке 1:
Можно ли за какое-нибудь количество ходов расположить этих коней так, как показано на рисунке 2?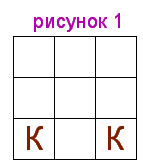
Задачи со спичками:
1) Переставьте три спички так, чтобы рыбка поплыла в обратном направлении. Другими словами, нужно повернуть рыбу на 180 градусов по горизонтали.

Решение: Для решения задачи будем передвигать спички, которые составляют нижнюю часть хвоста и туловища, а также нижний плавник нашей рыбы. Переместим 2 спички наверх, а одну вправо, как показано на схеме. Теперь рыбка плывет не вправо, а влево.
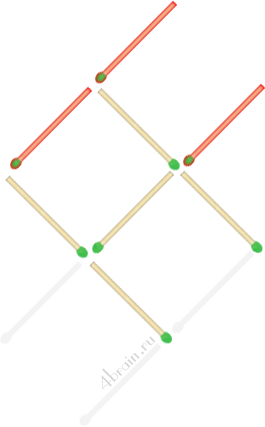
2) Перед Вами девять маленьких квадратов, образованных двадцатью четырьмя спичками. Уберите 8 спичек, не трогая остальных, чтобы осталось всего лишь 2 квадрата.

3) Переложите 2 спички так, чтобы образовать 7 квадратов.

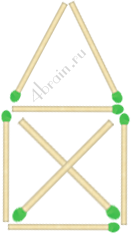
4) Передвиньте 2 спички так, чтобы вместо 9 треугольников остался только один.
Задачи на переправы и разъезды
1)Отряд солдат подходит к реке, через которую надо переправиться. Но мост сломан, а река глубока. Вдруг командир замечает двух мальчиков, которые катаются на лодке недалеко от берега. Но лодка так мала, что может выдержать только одного солдата или только двух мальчиков — не больше! Однако все солдаты переправились через реку именно на этой лодке. Как это было сделано?
Решение: Дети переехали реку. Один из мальчиков остался на берегу, а другой пригнал лодку к солдатам и вылез. После этого в лодку сел солдат и переправился на другой берег. Мальчик, оставшийся там, пригнал лодку обратно к солдатам, взял своего товарища, отвёз на другой берег и снова доставил лодку обратно, после чего вылез, а в неё сел другой солдат и переправился через реку. Таким образом, после каждых двух перегонов лодки через реку и обратно переправлялся один солдат. Так повторялось столько раз, сколько было солдат.
2) Крестьянину надо перевести через реку волка, козу и капусту. Но в лодке может поместиться только крестьянин, а с ним или только волк, или только коза, или только капуста. Но если оставить волка с козой, то волк съест козу, а если оставить козу с капустой, то коза съест капусту. Как перевёз свой груз крестьянин?
3) По каналу один за другим идут три парохода: А, Б, В. Навстречу им показались ещё три парохода, которые тоже идут один за другим: Г, Д, Е. Канал такой ширины, что два парохода в нём разъехаться не могут, но в канале с одной стороны есть залив, в котором может поместиться только один пароход. Могут ли пароходы разъехаться так, чтобы продолжать свой путь по-прежнему
4) К берегу реки подошли 3 контрабандиста с двумя мешками золота каждый. У берега нашлась трехместная лодка в которую помещались любые три мешка, или контрабандист + 2 мешка, или 2 контрабандиста + 1 мешок или 3 контрабандиста. Каждый из преступников не может оставить ни один из своих мешков наедине с другими преступниками, но может их оставить на безлюдном берегу. Могут ли все они переправиться через реку?
5) Семья (папа, мама, сын и бабушка) ночью подошла к мосту, способному выдержать только двух человек одновременно. По мосту можно двигаться только с фонариком. Известно, что папа может перейти мост в одну сторону за минуту, мама — за две, сын — за пять и бабушка — за десять минут. Фонарик у них один. Светить издали нельзя. Носить друг друга на руках тоже. Если по мосту идут двое, время перехода определяется наиболее медлительным членом семьи. Как семье переправиться за 17 минут?
Задачи на разрезание:
1) Существует ли 10-угольник, который можно разрезать на 5 треугольников?
Решение: Существует
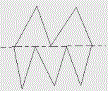
2) Попробуйте разрезать изображенную на рисунке фигуру на 3 равные по форме части:
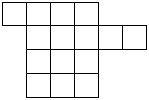
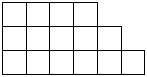
3) Разрежьте данную фигуру на 5 равных по форме частей:
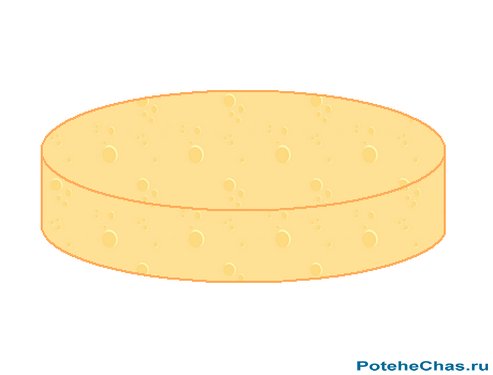
4) Попробуйте тремя движениями ножа разрезать сыр на восемь равных кусков.
5) Каким образом необходимо разрезать данный крест, чтобы из полученных кусков можно было собрать квадрат с пустотой внутри него в виде такого же по форме и размерам креста.
Задачи с числами.
1)Напишите подряд семь цифр от 1 до 7: 1 2 3 4 5 6 7.Необходимо соединить их знаками плюс и минус так, чтобы получилось 40.
Решение: 12+34-5+6-7=40
2) Напишите подряд девять цифр от 1 до 9: 1 2 3 4 5 6 7 8 9.Необходимо соединить их знаками плюс и минус так, чтобы получилось 100.
3) Выразите единицу, употребив все 10 цифр.
4) Можно ли пятью двойками выразить число 28?
5) Можно ли записать пятью тройками и знаками действий число 10?
6) Можно ли выразить 1000 восемью одинаковыми цифрами и знаками действий?
7) Какие три целых числа, если их перемножить дают столько же, сколько получается от их сложения?
8) Напишите наибольшее девятизначное число, в котором нет повторяющихся цифр и которое делится без остатка на 11
9)Расшифруйте запись примера на сложение.
А Б В Д
+ А Б Г Д
В Д Г А Д
Литература: 1) Эдуард Балаян: 700 лучших олимпиадных и занимательных задач по математике. 5-6 классы
2) http://4brain.ru
3) http://math.all-tests.ru
Олимпиадные задачи по математкие 5-6 класс — Колпаков Александр Николаевич
В последнее время увеличился поток писем от посетителей сайта с просьбами о помощи в решении олимпиадных задач для самых маленьких (5 — 6 класс). Это приятно, ибо работать с талантливыми и целеустремленными детьми одно удовольствие. Кто обычно пишет репетитору по математике? Как правило, это родители учеников, решающих сложные задачи для собственного удовлетворения и развития. Чуть меньше писем от самих участников математических олимпиад и конкурсов «Кенгуру». Последние присылают задачи, оказавшиеся им не по зубам на школьном или на районном туре. Репетитор по математике он-лайн в таких случаях является хорошим источником проверки правильности решения, а иногда и единственной надеждой узнать его вообще. Не каждому родителю удается справиться с олимпиадной задачей (и тем более объяснить ее в 5 классе), а возможности придти после олимпиады домой и посмотреть решение задачи в учебнике нет. Именно для таких посетителей я решил открыть новую узкоспециализированную страницу: олимпиадные задачи по математике для 5 — 6 класса.
К сожалению, не всегда удается найти время на полное оформление задач в том объеме, в котором ни приходят ко мне по e-mail. Не забывайте, что я реальный репетитор по математике, а не виртуальный. Поэтому заранее прошу прощения, если в силу своей занятости не смогу ответить Вам оперативно. Оформление каждого решения (особенно если нужны рисунки и схемы) отнимает много времени и отвлекает репетитора от самого главного — от реальных занятий. Но мне интересно развитие сайта, интересно расширение базы занимательных задач (дефицит которых испытывает каждый репетитор по математике), поэтому в свободное время с удовольствием работаю с Вашими письмами. Пишите, присылайте интересные и сложные задачки (для 5 класса, для 6 класса !!!), присылайте все что Вам показалось занимательным и необычным, сложным, тонким или противоречивым.
Олимпиадные задачи для 5 — 6 класса. Ответы на Ваши вопросы.
Вопрос репетитору по математике от Валентины
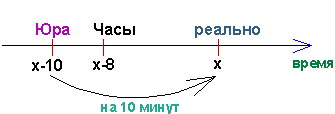
Часы Юры отстают на 8 минут, но он считает, что часы спешат на 2 минуты. Часы Коли спешат на 2 минуты, однако он думает, что они отстают на 8 минут. Друзья договорились, что встретиться в 5 часов вечера. Кто раньше окажется у места встречи и на сколько минут?
Решение репетитора (Колпаков А.Н.)
Отметим, что мальчики приходят в точку встречи по своему «внутреннему» таймеру (который рассчитывают), а не по реальному. Поэтому надо узнать, каково реальное время в момент прихода каждого. Найдем разницу между реальным временем и тем временем, которое представляет себе Юра. Пусть точное время x минут, тогда на часах Юры x-8 минут. Так как он думает, что они спешат, значит считает, что сейчас x-8-2 минут. Поэтому значение реального времени больше того, которое представляет себе Юра на 10 минут. Это означает, что к моменту прихода Юры в точку встречи реальное время составит 17 ч 10 мин.
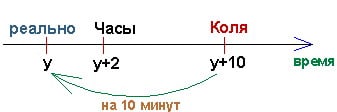
 Аналогично рассуждая можно получить расклад по Коле. Пусть y (мин) — реальное время. Тогда часы Коли в этот момент показывают y+2 (мин). Так как он думает, что часы отстают на 8 минут, значит считает, что в этот момент y+2+8 минут.
Аналогично рассуждая можно получить расклад по Коле. Пусть y (мин) — реальное время. Тогда часы Коли в этот момент показывают y+2 (мин). Так как он думает, что часы отстают на 8 минут, значит считает, что в этот момент y+2+8 минут.
Поэтому значение реального времени меньше представляемого Колей на 10 минут. Это значит, что к моменту прихода Коли реально 16 ч 50 мин. Поэтому Коля пришел раньше Юры на 20 минут. 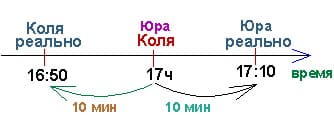
Задача репетитору по математике от Катерины.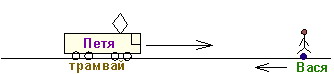 Доброе утро, ребёнку в школе задали решить задачу с олимпиады, ну ни как не получается! Задача: Петя в трамвае заметил Васю, который поравнялся с трамваем следуя вдоль трамвайных путей в противоположном направлении. Через минуту Петя вышел и побежал вдогонку за Васей вдвое быстрее его, но в 4 раза медленнее трамвая. Через какое время Петя догонит Васю? Помогите.
Доброе утро, ребёнку в школе задали решить задачу с олимпиады, ну ни как не получается! Задача: Петя в трамвае заметил Васю, который поравнялся с трамваем следуя вдоль трамвайных путей в противоположном направлении. Через минуту Петя вышел и побежал вдогонку за Васей вдвое быстрее его, но в 4 раза медленнее трамвая. Через какое время Петя догонит Васю? Помогите.
Решение (А.Н.Колпаков) Прежде всего, нужно понять, что означает «в два раза быстрее». Это значит, что скорость больше в два раза. А поэтому в два раза больше будет пройденное расстояние (не важно, за какое время). Тогда, если Петя идет в два раза быстрее Васи и в 4 раза медленнее трамвая, то Вася проходит за минуту в 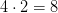 раз меньшее расстояние, чем трамвай.
раз меньшее расстояние, чем трамвай.
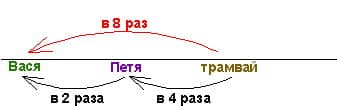 Поэтому если за одну минуту Вася проходит какой-то отрезок пути, то трамвай проезжает 8 таких отрезков. Поэтому расстояние между мальчиками в момент выхода Пети составляет 9 отрезков. За ту же минуту Петя проходит 2 отрезка (раз его скорость в 2 раза больше). Введем единицу измерения длины, равную этому же отрезку. Тогда мы имеем стандартные начальные данные для самой обычной задачи на скорость сближения. Скорости мальчиков известны – это 1 (отрезок/мин) и 2 (отрезка/мин), а расстояние для сближения составляет 9 отрезков.
Поэтому если за одну минуту Вася проходит какой-то отрезок пути, то трамвай проезжает 8 таких отрезков. Поэтому расстояние между мальчиками в момент выхода Пети составляет 9 отрезков. За ту же минуту Петя проходит 2 отрезка (раз его скорость в 2 раза больше). Введем единицу измерения длины, равную этому же отрезку. Тогда мы имеем стандартные начальные данные для самой обычной задачи на скорость сближения. Скорости мальчиков известны – это 1 (отрезок/мин) и 2 (отрезка/мин), а расстояние для сближения составляет 9 отрезков.
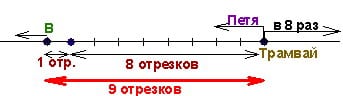 За каждую минуту оно сокращается на 2-1=1 отрезок (это и есть скорость сближения). А нам надо узнать, за какое время расстояние в 9 отрезков сократится до нуля, то есть надо узнать время сближения. Его можно найти, разделив путь сближения на скорость сближения. Поэтому 9 делим на 1 и получаем 9 минут. Ответ: 9 мин.
За каждую минуту оно сокращается на 2-1=1 отрезок (это и есть скорость сближения). А нам надо узнать, за какое время расстояние в 9 отрезков сократится до нуля, то есть надо узнать время сближения. Его можно найти, разделив путь сближения на скорость сближения. Поэтому 9 делим на 1 и получаем 9 минут. Ответ: 9 мин.
Вопрос репетитору по математике от Ибрагилава.
Как решить задачу? Свете втрое больше лет, чем было Максиму тогда, когда она была в его нынешнем возрасте. Когда Максим будет в возрасте Светы, то им вместе будет 28 лет. Сколько сейчас лет Максиму и сколько сейчас лет Свете?
Решение (Колпаков А.Н.)
Запутанные (олимпиадные) задачи на возраст удобно показывать на временной оси, на которой возраста представляются точками. Если у нас 2 человека и их возраста меняются, то изображающие их точки будут просто двигаться по оси. При этом расстояние между ними (разница в возрасте) будет сохраняться. Покажем нынешний возраст Светы и Максима точками С и М (верхний ряд букв на рисунке). В нижнем ряду поставим буквы С и М для того момента, когда «Света была в нынешнем возрасте Максима». 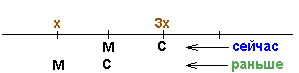 Получим равные отрезки, концы которых (нижняя М и верхняя С) согласно условию «в 3 раза» можно обозначить как х и 3х. Тогда нынешний возраст Максима (середина отрезка) будет иметь координату 2х, а значит разница в возрасте составит ровно х (лет). Теперь покажем, какими будут координаты возрастов в тот момент, когда Максим окажется в возрасте Светы. Эти буквы стоят в ряду «будущее».
Получим равные отрезки, концы которых (нижняя М и верхняя С) согласно условию «в 3 раза» можно обозначить как х и 3х. Тогда нынешний возраст Максима (середина отрезка) будет иметь координату 2х, а значит разница в возрасте составит ровно х (лет). Теперь покажем, какими будут координаты возрастов в тот момент, когда Максим окажется в возрасте Светы. Эти буквы стоят в ряду «будущее». 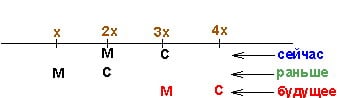 Длина их отрезка тоже равна х (лет) и поэтому возраст Светы в этот момент окажется равным 4х (лет). Так как в будущем им вместе будет 28 лет, то 3х+4х=28, откуда получаем, что х=4. Поэтому Максиму сейчас
Длина их отрезка тоже равна х (лет) и поэтому возраст Светы в этот момент окажется равным 4х (лет). Так как в будущем им вместе будет 28 лет, то 3х+4х=28, откуда получаем, что х=4. Поэтому Максиму сейчас 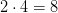 лет, а Свете сейчас
лет, а Свете сейчас 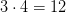 лет.
лет.
Вопрос репетитору по математике от Миши
Здравствуйте! Помогите решить олимпиадную задачку за 5 — 6 класс. Вася написал в тетради 4 числа. Сложил их по два всеми возможными способами получил шесть таких сумм: 2, 4, 9, 9, 14, 16. Какие числа записал Вася?
Решение (Колпаков А.Н.)
Пусть a, b, с, d – искомые числа, расположенные в порядке возрастания. Составим последовательность их суммы также в порядке возрастания используя неравенство a < b < c < d. Получим такой ряд:
1) a+b=2
2) a+c=4
3,4) b+c и a+d
5) b+d=14
6) c+d=16
Первые две суммы явно наименьшие и поэтому равны 2 и 4. Две последние явно наибольшие и равны соответственно 14 и 16. Осталось выяснить судьбу двух оставшихся: b+с и a+d. Но так на них приходятся две девятки, то каждая из них равна 9. По первым двум суммам делаем вывод, что с на 2 больше чем b. Поэтому c=b+2. Подставляя выражение для числа с в равенство b+c=9 получим, что b+b+2=9. Поэтому b=3,5 и значит c=3,5+2=5,5. Из первого равенства вытекает, что a=2-3,5=-1,5, а из последнего, что d=16-5,5=10,5
В итоге ответ оказывается таким: -1,5; 3,5; 5,5 и 10,5
Задача репетитору от Эльдара. Помогите решить: Всего 5555 человек, на 10 солдат приходится 1 капрал, на 5 капралов 1 офицер, на 9 офицеров 1 генерал. Решение: сколько всего было солдат?
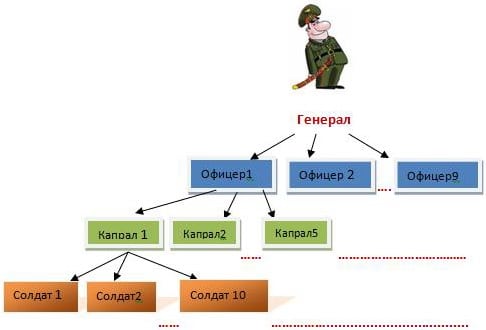
Репетитор по математике Ермакова Диана
Для начала определим, сколько человек в одном таком «наборе», состоящем из генерала, капралов, офицеров и солдат.
Один генерал и девять офицеров у нас уже есть. Так как на каждого офицера приходится 5 капралов, то на 9 офицеров приходится 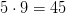 капралов.
капралов.
Так как на каждого капрала приходится 10 солдат, то на 45 капралов приходится 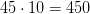 солдат.
солдат.
Всего человек в «наборе» 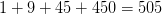
Так как всего в армии 5555 человек, то количество «наборов» равно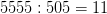 . В одном «наборе»
. В одном «наборе» 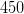 солдат, поэтому в 11 «наборах» будет
солдат, поэтому в 11 «наборах» будет 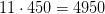 солдат.
солдат.
Ответ: 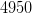 солдат.
солдат.
Иногда мне помогают оформлять решения другие репетиторы по математике. Я рассылаю условия тем, кто дал свое согласие на участие в виртуальной работе. Для репетитора по математике такая активность — хороший шанс обратить на себя внимание будущих учеников. Поэтому, если Вы регистрируетесь у меня на сайте как репетитор по математике — укажите при заполнении анкеты (в поле дополнительной информации) готовы ли Вы к такому сотрудничеству. Тот репетитор по математике, кто будет присылать решения для публикации регулярно, скорее всего, может рассчитывать на размещение еще и в рекомендованном списке репетиторов.
Pages: 1 2
Олимпиадные задания по математике (5, 6 класс): Задания по математике для школьного этапа олимпиады 5-6 КЛАССЫ.
Задания школьного этапа олимпиады
МАТЕМАТИКА
2017-2018 учебный год
5 класс.
1. 5. На прямой взяли четыре точки. Сколько всего получилось отрезков, концами которых являются эти точки?
2.5. Требуется распилить бревно на 6 частей. Каждый распил занимает 2 минуты. Сколько времени потребуется на эту работу?
3.5. С хозяйством попа справляются 10 работников. Каждый работник в день съедает каравай хлеба и другие продукты. Поп принял на работу Балду.
Живет Балда в поповом доме,
Спит себе на соломе,
Ест за четверых,
Работает за семерых.
Поп прогнал лишних работников. Сколько караваев хлеба экономил поп ежедневно?
4.5. Турист поднимался в гору 5 часов, проходя каждый час 3 км. На обратном пути он увеличил скорость на 2 км/ч. Сколько часов потребовалось туристу на обратный путь?
5.5. Винни-Пуху подарили в день рождения бочонок с мёдом массой 7кг. Когда Винни-Пух съел половину мёда, то бочонок с оставшимся мёдом стал иметь массу 4кг. Сколько килограммов мёда было первоначально в бочонке?
Задания школьного этапа олимпиады
МАТЕМАТИКА
2017-2018 учебный год
6 класс.
1.6. В школе 500 учеников. Почему среди них обязательно найдутся хотя бы двое, родившихся в один и тот же день года?
2.6. Расставьте скобки в выражении 7 – 6 – 5 – 4 – 3– 2 – 1 = 0 так, чтобы получилось верное равенство.
3.6. В пенале лежит 10 ручек. Известно, что, по крайней мере, одна из ручек красная. Также известно, что если из пенала взять любые две ручки, то среди них обязательно будет синяя. Сколько красных ручек может быть в пенале? Объясните свой ответ.
4.6. В ящике 23 кг гвоздей. Как с помощью чашечных весов и одной гири в 1 кг за два взвешивания отмерить 5 кг гвоздей?
5.6. Петя утверждает, что позавчера ему было 10 лет, а в будущем году исполнится 13. Возможно ли это? Свой ответ объясни.
Олимпиадные задания по математике 5,6,7,8,9,10 классы
Решение заданий олимпиады по математике (школьный тур)
5 класс
1. Сколько всего трехзначных чисел? Ответ. 900
Решение. Первое трехзначное число 100, последнее – 999. Всего
999 чисел от 1 до 999, из них нам не нужны 99 чисел – от 1 до 99. Поэтому нужных 999-99=900.
Комментарий. Можно было посчитать, использую комбинаторику:
для первой цифры 9 вариантов, для второй 10, для третьей 10, итого 9*10*10=900 комбинаций.
2. Календарь представляет собой два кубика, у каждого кубика на всех гранях написано по цифре. Дату (день месяца) составляют, используя один или два кубика. Придумайте, как написать цифры
на кубиках, чтобы можно было получить любую дату от 1 до 31. (В ответе напишите, какие цифры должны быть на одном кубике, а какие – на другом.)
Решение. Например, на одном кубике написаны цифры 0, 1, 2, 4, 5, 6 а на другом 1, 2, 3, 7, 8, 9. Замечание. Существуют и другие примеры. Для проверки правильности примера, достаточно проверить, что 1) в каждой группе по 6 цифр, 2) все цифры встречаются, 3) можно составить числа 11, 22 и 30 (т.е. в каждой группе есть цифры 1 и 2, а цифры 0 и 3 находятся в разных группах).
3. Разрежьте фигуру на рисунке справа на 4 равные части. 
4. Три математика ехали в разных вагонах одного поезда. Когда поезд подъезжал к станции, математики насчитали на перроне 7, 12 и 15 скамеек. А когда поезд отъезжал, один из них насчитал еще 2 скамейки. Сколько насчитали остальные?
Ответ. 5 и 10 скамеек. Решение. Очевидно, что тот, кто до остановки проехал большую часть перрона, насчитал большее число скамеек. Пусть первый насчитал 15 скамеек, второй 12, третий 7. Так как первый насчитал на 3 скамейки больше, чем второй, то, когда поезд будет отъезжать, второй увидит эти 3 скамейки, т.е. насчитает на 3 скамейки больше, чем первый. Аналогично третий насчитает на 8 скамеек больше, чем первый. Раз кто-то насчитал 2 скамейки, то это мог быть только первый. Значит, остальные насчитали 2+3=5 и 2+8=10 скамеек.
5. Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Без Мышки все остальные не могут вытащить репку, а вместе с Мышкой – могут. Сколько мышек надо собрать вместе, чтобы эти мышки смогли вытащить репку сами?
Ответ. 1237 мышек. Решение. Кошка = 6 мышек; жучка = 5 кошек = 30 мышек; внучка = 4 жучки = 120 мышек; бабка = 3 внучки = 360 мышек; дедка = 2 бабки = 720 мышек.
Все вместе дедка+бабка+внучка+жучка+кошка+мышка = 720+360+120+30+6+1=1237 мышек.
6. Мальчик Сережа увидел двоих двухголовых дракончиков, головы которых спутались. Драконы бывают либо правдивые, т.е. обе головы говорят только правду, либо лживые, т.е. обе головы
всегда лгут. Сережа решил помочь дракончикам распутать головы. Но для этого ему надо знать, где чья голова. Он спросил это у дракончиков, на что головы ответили:
первая: «я – правдивая голова»;
вторая: «третья голова – моя родная голова»;
третья: «вторая голова – не родная мне голова»;
четвертая: «третья голова – лживая».
Какие головы принадлежат каким дракончикам?
Ответ. Третья и первая головы от одного (правдивого) дракона, а вторая и четвертая – от другого (лживого).
Решение. Вторая и третья головы противоречат друг другу, значит, они не родные (родные головы либо обе скажут, что они родные, либо обе скажут, что они не родные). А значит, третья голова сказала правду (т.е. она правдивая), а вторая солгала (т.е. она лживая). Значит, четвертая голова солгала, сказав, что третья лживая, т.е. родная второй голове. А тогда третья родная первой.
Комментарии по проверке
Каждая задача оценивается из 7 баллов. Каждая оценка – целое число от 0 до 7. Ниже приведены некоторые указания к проверке. При оценке решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) – тогда решение
оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.
Задача 1. Правильный ответ без обоснования – 3 балла. Выражение 999-99=900 или 999100+1=900 является достаточным обоснованием. Выражение 1000-100=900 без дополнительных пояснений обоснованием не считается.
Задача 2. Правильное распределение – 7 баллов. Голый неправильный пример – 0 баллов. Сказано, что 1 и 2 должны быть на обоих кубиках, т.к. есть числа 11 и 22, а дальше пример
неправильный из-за того, что 0 и 3 поместили на один кубик – 2 балла.
Задача 3. Правильное разрезание – 7 баллов. Разрезание на равные по площади, но не равные части – 0 баллов.
Задача 4. Ответ без обоснования – 2 балла.
Задача 5. Есть идея все выражать в мышках, но не доведено до конца или неправильно доведено (например, посчитано, что дедка — это 720 мышек и в ответ записано 720 ) – 2 балла. Вычислительная ошибка – минус 1 балл (если вычислительных ошибок несколько, соответственно вычитается больше).
Задача 6. Правильный ответ 1 балл. Правильный ответ и проверка – все равно 1 балл. Неполный перебор, какие головы кому принадлежат, добавляет не больше 2 баллов.
6 класс
1. Календарь представляет собой два кубика, у каждого кубика на всех гранях написано по цифре. Дату (день месяца) составляют, используя один или два кубика. Придумайте, как написать цифры
на кубиках, чтобы можно было получить любую дату от 1 до 31. (В ответе напишите, какие цифры должны быть на одном кубике, а какие – на другом)
Решение. Например, на одном кубике написаны цифры 0, 1, 2, 4, 5, 6 а на другом 1, 2, 3, 7, 8, 9.
Замечание. Существуют и другие примеры. Для проверки правильности примера, достаточно проверить, что 1) в каждой группе по 6 цифр, 2) все цифры встречаются, 3) можно составить
числа 11, 22 и 30 (т.е. в каждой группе есть цифры 1 и 2, а цифры 0 и 3 находятся в разных группах).
2. Одной черепахе 300 лет, а другой 15 лет. Через сколько лет первая черепаха будет вдвое старше второй? Ответ. Через 270 лет.
Решение. Разница между черепахами всегда 300-15=285 лет. Одна будет вдвое старше другой, когда второй будет столько лет, какова разница, т.е. 285. А 285 лет второй черепахе исполнится через 285-15=270 лет.
3. Сад разбит на квадраты. Садовник начал обход с верхнего правого квадрата, обошел весь сад и
вернулся в тот же угловой квадрат. В закрашенных квадратиках он не был (там располагаются пруды). Во всех остальных квадратиках он побывал по одному разу, причем через вершины квадратов он не проходил. Начертите возможный путь садовника.
Ответ. Один из возможных примеров обхода приведен на рисунке 
(возможны и другие пути).
4. На некотором острове каждый житель либо всегда лжет, либо всегда говорит правду. Трое островитян А, Б, В сказали следующее:
А: «Б – лжец»; Б: «ровно один из А и В лжец»; В: «у меня есть крокодил». Есть ли у В крокодил?
Ответ. Да, есть. Решение. Первый способ. 1) Пусть А говорит правду. Тогда Б – лжец.
Тогда А и В оба лжецы или оба «правдивцы», но т.к. А –
«правдивец», то и В «правдивец», т.е. крокодил у него есть.
2) Пусть А – лжец. Тогда Б – «правдивец». Тогда ровно один из А
и В лжец, но т.к. А лжец, то В – «правдивец». Т.е. крокодил у него есть.
Таким образом, в обоих случаях получаем, что у В есть крокодил.
Второй способ. 1) Пусть Б «правдивец». Тогда ровно один из А и В лжец, но т.к. А говорит, что Б лжец, то А – лжец => В «правдивец» => крокодил у него есть.
2) Пусть Б лжец. Тогда оба А и В «правдивцы», или оба лжецы. Но А говорит, что Б лжец, т.е. говорят правду = > они оба (А и В) «правдивцы», т.е. у В есть крокодил.
5. Прямоугольник разрезали на три прямоугольника, два из которых имеют размеры 5×11 и 4×6. Какие размеры мог иметь третий прямоугольник? (Найдите все возможности.)
Ответ. 5×4, 7×6, 1×6, 1×11.
Решение. Посмотрим, как могут прилегать прямоугольники друг к другу.
Прямоугольник 4×6 может примыкать к стороне 5 или к стороне 11, при этом прилегать он может стороной 4 или стороной 6, т.е. всего 4 варианта: Из них получаем размеры третьего прямоугольника: 5×4, 7×6, 1×6, 1×11.
6. Винни-Пуху дали полную тарелку манной каши. Он съел половину и положил в тарелку еще столько же меда. Затем он съел треть содержимого тарелки (каши с медом) и снова доложил мед. Потом съел четверть содержимого и опять доложил медом, после чего с аппетитом все съел. Чего в итоге Винни-Пух съел больше: каши или меда?
Ответ. Меда он съел больше.
Решение. Видно, что Пух в итоге съел тарелку каши. Посчитаем, сколько он съел меда: 1/2+1/3+1/4 = 13/12>1.
Комментарии по проверке
Каждая задача оценивается из 7 баллов. Каждая оценка – целое число от 0 до 7.
При оценке решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) – тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.
Задача 1. Правильное распределение – 7 баллов. Только неправильный пример – 0 баллов. Сказано, что 1 и 2 должны быть на обоих кубиках т.к. есть числа 11 и 22, а дальше пример
неправильный из-за того, что 0 и 3 поместили на один кубик – 2 балла.
Задача 2. Только ответ без всяких пояснений – 2 балла.
Задача 3. Правильный пример – 7 баллов. Пример незамкнутого пути или пути не по всем клеткам – 0 баллов.
Задача 4. Голый ответ «Да, есть» – 0 баллов. Разобран только один случай, например, что А – «правдивец» – 1 балл.
Задача 5. Найдены все варианты (подтверждены картинками), но нет никаких объяснений, почему это именно ВСЕ варианты – 5 баллов.
Найдены только три из четырех вариантов – 2 балла. Найдено два
варианта – 1 балл. Найден только один вариант – 0 баллов.
Задача 6. Голый ответ 0 баллов.
7 класс
1. Замените буквы цифрами так, чтобы получилось верное равенство: О + Л + И + М + П + И + А = ДА (Одинаковые буквы надо заменять одинаковыми цифрами, разные – разными, ДА – двузначное число)
Ответ. Например, О=3, Л=4, И=0, М=5, П=8, Д=2, А=9.
Решение. Вычтем из обоих частей уравнения А, получим, что сумма цифр О+Л+И+М+П+И должна заканчиваться на ноль. Попробуем подобрать цифры так, чтобы например она была
равна 20 (т.е. Д=2). Это легко сделать, например 3+4+0+5+8+0 =20. т.е. О=3, Л=4, И=0, М=5, П=8, Д=2, А=9
Комментарий. Возможно много других решений. При этом Д может равняться 2, 3, 4.
2. На каждой перемене Робин-Бобин-Барабек съедает по конфете. За неделю (с понедельника по субботу) было 30 уроков. Сколько всего конфет съел Робин на переменах?
Ответ. 24 конфеты.
Решение. Если бы все эти уроки произошли в один день, то Робин съел бы 29 конфет (количество промежутков между 30 уроками). Но так как между последним уроком какого-то дня и первым
уроком следующего дня конфета не съедается, то нужно еще вычесть 5 конфет (по количеству промежутков между шестью днями), т.е. итого получается, что Робин съел 30 – 5=24 конфеты.
3. Из двух одинаковых железных проволок кузнец сковал по железной цепи. Первая содержит 80 звеньев, а вторая – 100. Каждое звено первой цепи на 5 граммов тяжелее каждого звена
второй цепи. Какова масса цепей?
Ответ. 2 кг.
Первое решение. Пусть x г – масса каждого звена второй цепи, тогда (x+5) г – масса каждого звена первой цепи. Тогда масса проволоки, с одной стороны, равна 100x, а с другой 80(x+5) г. Из
равенства 100x=80(x+5) следует, что x=20, а масса одной проволоки 100*20 г = 2 кг.
Второе решение. Т.к. массы цепей одинаковы, то, «забрав» у каждого звена первой цепи по 5 г, мы получим 80 кусочков по массе таких же, как звенья второй цепи, а из излишков должны
получиться оставшиеся 20 звеньев. Т.е. 20 звеньев весят 5*80=400 г, а одно звено второй цепи весит 400:20=20 г. Поэтому все 100 звеньев весят 100*20=2000 г, т.е. 2 кг.
4. Углы АОВ, ВОС и СОD равны между собой, а угол АОD втрое меньше каждого из них. Все лучи ОА, ОВ, ОС, ОD различны. Найдите величину угла AOD (перечислите все возможные варианты).
Ответ. 36, 45 градусов.
Решение. Углы АОВ, ВОС и СОD следуют друг за другом в одном направлении (т.к. никакие лучи не совпадают). При этом их сумма может быть меньше 360(см. рис 1) и больше 360 (см. рис. 2).
Обозначим величину угла АОD через x. Тогда каждый из углов АОВ, ВОС и СОD равен 3x. В первом случае получается, что 3x+3x+3x+x=360, откуда x=36. Во втором 3x+3x+3x-x=360, откуда x=45.
5. На некотором острове каждый житель либо всегда лжет, либо всегда говорит правду. Трое островитян А, Б, В сказали следующее: А: «Б – лжец»; Б: «ровно один из А и В лжец»;
В: «у меня есть крокодил». Есть ли у В крокодил?
Ответ. Да, есть.
Решение. Первый способ. 1) Пусть А говорит правду. Тогда Б – лжец. Тогда А и В оба лжецы или оба «правдивцы», но т.к. А – «правдивец», то и В «правдивец», т.е. крокодил у него есть.
2) Пусть А – лжец. Тогда Б – «правдивец». Тогда ровно один из А и В лжец, но т.к. А лжец, то В – «правдивец». Т.е. крокодил у него есть.
Таким образом, в обоих случаях получаем, что у В есть крокодил.
Второй способ. 1) Пусть Б «правдивец». Тогда ровно один из А и В лжец, но т.к. А говорит, что Б лжец, то А – лжец => В «правдивец» => крокодил у него есть.
2) Пусть Б лжец. Тогда оба А и В «правдивцы», или оба лжецы. Но А говорит, что Б лжец, т.е. говорят правду = > они оба (А и В) «правдивцы», т.е. у В есть крокодил.
6. Имеется 6 гирь: по паре зеленых, красных и белых. В каждой паре одна гиря тяжелая, а другая – легкая, причем все легкие весят одинаково и все тяжелые весят одинаково. Можно ли определить
3 тяжелые гири за два взвешивания на чашечных весах? (Чашечные весы показывают, равны ли веса грузов на чашках, а если не равны, то какая чашка тяжелее.)
Ответ. Да.
Решение. Обозначим зеленые гири З1 и З2, аналогично гири других цветов К1, К2, Б1, Б2. Первое взвешивание: (К1+Б1) =? (К2+З1) 1) (К1+Б1) = (К2+З1). Возможные варианты:
а) К1>К2 и Б1<З1; б) К1<К2 и Б1>З1. Вторым взвешиванием сравниваем Б1 и З1 и выясняем какая из них тяжелая, какая легкая и соответственно какая легкая, а какая тяжелая из К1 и К2.
2) (К1+Б1) < (К2+З1). В этом случае К1 должна быть легче К2, а Б1 и Б2 могут быть: а) равные и при этом обе легкие б) равные и при этом обе тяжелые, в) Б1 легкая, З1 – тяжелая. Вторым взвешиванием сравниваем Б1 и З2: Б1<З2 => Б1 – легкая, З1 – легкая; Б1=З2 => Б1 и З1 разные, т.е. Б1 легкая, т.е. легкие Б1 и З2; Б1>З2 => Б2, З2 – легкие. 3) (К1+Б1) > (К2+З1). Аналогично случаю 2)
Комментарии по проверке
Каждая задача оценивается из 7 баллов. Каждая оценка – целое число от 0 до 7. Ниже приведены некоторые указания к проверке. Естественно, всех случаев жюри предвидеть не может. При оценке решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) – тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.
Задача 1. Правильный пример – 7 баллов. Если есть идея подбирать сумму О+Л+И+М+П+И так, чтобы она заканчивалась на 0: 2 балла.
Задача 2. Только ответ – 1 балл. Ответ на примере – 2 балла. Далее в зависимости от полноты обоснований – от 3 до 7 баллов.
Задача 3. Только ответ – 1 балл. Верный ответ с проверкой (сказано, сколько должно весить каждое звено) – 3 балла. Верно составлено уравнение, которое затем решается подбором – не более 5 баллов.
Задача 4. За один из ответов 360 или 450, снабженный пояснениями (хотя бы в виде чертежей). – 3 балла. Только один из ответов без пояснений 1 балл. Оба ответа написаны, но нет никаких пояснений, – 3 балла.
Задача 5. Только ответ «Да» – 0 баллов. Разобран только один случай, например, что А – «правдивец»: 1 балл.
Задача 6. Приведены верные взвешивания, из которых делаются правильные выводы какие гирьки тяжелые/легкие – 7 баллов. Если хотя бы одно из взвешиваний неправильное (в итоге нельзя сделать однозначного вывода, какие гирьки какие) – 0 баллов. Приведена только верная последовательность взвешиваний, но никаких выводов и пояснений, почему она работает, нет – 4 балла.
8 класс
1. Числитель дроби увеличили на 5, а знаменатель – на 2 (числитель и знаменатель – целые положительные числа). При этом значение дроби уменьшилось. Приведите пример, как такое могло произойти. Ответ. Например, 10/3.
Комментарий. Подойдет любая дробь, большая чем 5/2.
2. Дано трехзначное число ABB. Если перемножить его цифры, то получится двузначное число АС, а если перемножить цифры АС, то получится С. Найдите исходное число.
Ответ. 144.
Решение. Так как А*С=С, то А=1 или С=0.
Первый случай: А=1. Тогда А*В*В=В2=1С, но есть только один квадрат между 10 и 20 – это 16, т.е. С=6. Откуда В=4. Т.е. исходное число 144: А=1, В=4, С=6.
Второй случай: С=0. Тогда А*В*В=А0=10А. Т.к. А – первая цифра, то А.0, можем сократить на А. Получим В2=10 – нет решения. Таким образом, ответ единственный.
3. Три математика ехали в разных вагонах одного поезда. Когда поезд подъезжал к станции, математики насчитали на перроне 7, 12 и 15 скамеек. Когда поезд отъезжал, каждый из них насчитал еще несколько скамеек, причем один из них насчитал в три раза больше, чем другой. А сколько насчитал третий?
Ответ. 7 скамеек.
Решение. Очевидно, что тот, кто до остановки проехал большую часть перрона, насчитал большее число скамеечек. Пусть первый насчитал 15 скамеек, второй 12, третий 7. Так как первый насчитал на 3 скамейки больше, чем второй, то, когда поезд будет отъезжать, второй увидит эти 3 скамейки, т.е. насчитает на 3 скамейки больше, чем первый. Аналогично третий насчитает на 8 скамеек больше, чем первый, и на 5 скамеек больше, чем второй. Раз кто-то насчитал в 3 раза больше, чем другой, то разница между насчитанными ими скамейками – четное
число (3x-x=2x). В нашем случае разность насчитанных скамеек четна только между первым и третьим и она равна 8. Значит, первый насчитал 8:2=4 скамейки, тогда второй 4+3=7 скамеек.
Замечание. Можно было обойтись и без четности. Пусть первый насчитал x скамеек. Тогда второй x+3, а третий x+8. А дальше составить всевозможные пары и решить получившиеся три уравнения (один насчитал в три раза больше, чем другой в паре): 3x=x+3, 3x=x+8, 3(x+5)=x+8. Только одно из них имеет целое решение.
4. В треугольнике АВС (см. рисунок) CD – биссектриса угла ACB, АВ=ВС, BD=BK, BL=CL. Докажите, что BF – биссектриса угла CBE. 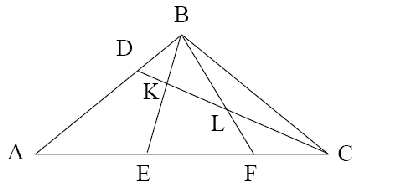
Решение. Обозначим (треугольник BDK – равнобедренный)
CBE.
5. Имеется 6 гирь: по паре зеленых, красных и белых. В каждой паре одна гиря тяжелая, а другая – легкая, причем все легкие весят одинаково и все тяжелые весят одинаково. Можно ли определить 3 тяжелые гири за два взвешивания на чашечных весах?
Ответ. Да.
Решение. Обозначим зеленые гири З1 и З2, аналогично гири других цветов К1, К2, Б1, Б2. Первое взвешивание: (К1+Б1) =? (К2+З1) 1) (К1+Б1) = (К2+З1). Возможные варианты:
а) К1>К2 и Б1<З1; б) К1<К2 и Б1>З1. Вторым взвешиванием сравниваем Б1 и З1 и выясняем какая из них тяжелая, какая легкая и соответственно какая легкая, а какая тяжелая из К1 и К2.
2) (К1+Б1) < (К2+З1). В этом случае К1 должна быть легче К2, а Б1 и Б2 могут быть: а) равные и при этом обе легкие б) равные и при этом обе тяжелые, в) Б1 легкая, З1 – тяжелая. Вторым взвешиванием сравниваем Б1 и З2: Б1<З2 => Б1 – легкая, З1 – легкая;
Б1=З2 => Б1 и З1 разные, т.е. Б1 легкая, т.е. легкие Б1 и З2; Б1>З2 => Б2, З2 – легкие
3) (К1+Б1) > (К2+З1). Аналогично случаю 2)
6. У каждого трехзначного числа нашли произведение его цифр. Получилось 900 произведений от 1*0*0 до 9*9*9 . Чему равна их сумма?
Ответ. 453=91125.
Решение. Достаточно заметить, что если мы раскроем скобки в произведении (1+2+…+9)·(0+1+2+…+9)·(0+1+2+…+9), то получим как раз 900 перечисленных в условии слагаемых, а все три суммы, стоящие в скобках, равны 45.
Комментарии по проверке
Каждая задача оценивается из 7 баллов. Каждая оценка – целое
число от 0 до 7. При оценке решения нужно исходить из того, является ли приведенное решение
в целом верным (хотя, может, и с недостатками) – тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.
Задача 1. Правильный пример дроби – 7 баллов.
Задача 2. Правильный ответ – 1 балл.
Верно разобран случай А=1, случай С=0 потерян – 3 балла.
Случай А разобран верно, в обосновании невозможности случая С=0 есть те или иные погрешности 4-6 баллов.
Задача 3. Голый ответ – 2 балла. Решение перебором по возможным парам (кто насчитал в три раза больше, чем другой), но какая-то пара из трех потеряна – не более 3 баллов.
Задача 5. Приведены верные взвешивания, из которых делаются правильные выводы какие гирьки тяжелые/легкие – 7 баллов. Если хотя бы одно из взвешиваний неправильное (в итоге нельзя сделать однозначного вывода, какие гирьки какие) – 0 баллов. Приведена
только верная последовательность взвешиваний, но никаких выводов и пояснений, почему она работает, нет – 4 балла.
Задача 6. За ответ без обоснования – 3 балла. С другой стороны, не надо требовать более подробного обоснования, чем в приведенном решении. Вычислять 453 не требуется.
9 класс
1. Придумайте такое нецелое число, что 15% и 33% от него – целые числа.
Ответ. Например, 100/3.
2. Туристам-байдарочникам нужны восемь одинаковых «сидушек» – мягких ковриков длиной не менее 35 см и шириной не менее 20 см. В спортивном магазине продаются большие коврики длиной 110 см и шириной 56 см. Хватит ли большого коврика на восемь «сидушек»?
Ответ. Да, хватит.
Решение. Разрежем большой коврик на два куска размерами 110×20 и 110×36. Из первого куска можно вырезать 3 «сидушки» размером 35×20 (и даже 36×20), а из второго куска – 5 «сидушек»
размером 35×20 (и даже 36×22).
Комментарий. Подсчет и сравнение площадей: 110*56=6160 – площадь большого ковра, 8*(35*20)=5600 – суммарная площадь маленьких, 6160>5600 – обоснованием не является. Например, большой ковер мог быть шириной 10 см, а длиной – километр.
Его площади хватило бы, однако ни одной «сидушки» из него вырезать нельзя.
3. Бумажный треугольник разрезали на два многоугольника прямолинейным разрезом, один из полученных многоугольников вновь разрезали на два и т. д. Какое наименьшее количество разрезов следует произвести, чтобы суммарное количество вершин у полученных многоугольников стало равно 400? Как это сделать?
Ответ. 100 разрезов.
Решение. Все получающиеся многоугольники выпуклые. Каждый разрез может идти:
а) из вершины в вершину;
б) из вершины к стороне;
в) от стороны к стороне.
В первом случае суммарное число вершин увеличивается на две, во втором – на три, в третьем – на 4. Таким образом, за один разрез общее число вершин может увеличиться максимум на 4.
Изначально у нас есть 3 вершины. Если разрезов было 99 или меньше, то общее число вершин будет 3+99*4=399<400. Таким образом, 99 разрезов не хватит. Чтобы получить 400 частей за 100 разрезов достаточно сделать 97 разрезов типа в – от стороны к стороне, и 3 разреза типа б – из вершины к стороне. Итого получится 3+97*4+3*3=400 частей.
Комментарий. Возможны и другие способы разрезания.
4. У разбойников есть 13 слитков золота. Имеются весы, с помощью которых можно узнать суммарный вес любых двух слитков. Придумайте, как за 8 взвешиваний выяснить суммарный вес всех слитков.
Решение. Возьмем три первых слитка и взвесим их попарно: С1+С2, С1+С3, С2+С3, затратив три взвешивания. Сложив результаты этих взвешиваний и поделив пополам, найдем суммарный вес этих трех слитков: ((С1+С2)+(С1+С3)+(С2+С3))/2 = С1+С2+С3. За оставшиеся пять взвешиваний найдем вес остальных 10 слитков: объединим их в 5 пар и взвесим каждую пару.
5. У каждого трехзначного числа нашли произведение его цифр. Получилось 900 произведений от 1*0*0 до 9*9*9 . Чему равна их сумма?
Ответ. 453=91125.
Решение. Достаточно заметить, что если мы раскроем скобки в произведении (1+2+…+9)·(0+1+2+…+9) ·(0+1+2+…+9), то получим как раз 900 перечисленных в условии слагаемых, а все три суммы, стоящие в скобках, равны 45.
6. Шестиугольник ABCDEF вписан в окружность. Докажите, что если AB||DE, AF||DC, то и BC||EF.
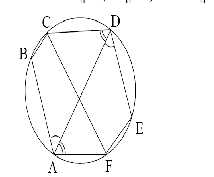
Решение. Так как АВ||DE, то
Так как четырехугольник ABCF – вписанный, то
Замечание. Можно было не использовать вписанные четырехугольники, а просто выразить оба угла BCF и CFE через дуги.
Комментарии по проверке
Каждая задача оценивается из 7 баллов. Каждая оценка – целое число от 0 до 7. При оценке
решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) – тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.
Задача 1. Правильный пример – 7 баллов.
Задача 2. Ответ без обоснования или с обоснованием, что площади хватает – 0 баллов. Ответ с объяснением, как резать – 7 баллов.
Задача 3. В задаче нужно сделать две вещи: 1) доказать оценку – что меньшим числом разрезаний не обойтись; 2) привести пример на данное число разрезаний. Если сделана только какая-то одна из этих двух вещей – 3 балла.
Только ответ «100 разрезаний» – 1 балл.
Задача 4. Правильные взвешивания и объяснение, как по их результатам узнать суммарный вес слитков – 7 баллов. Если используется запрещенное взвешивание (например, в какой-то момент взвешивается только один слиток) – 0 баллов.
Задача 5. За ответ без обоснования – 3 балла. С другой стороны, не надо требовать более подробного обоснования, чем в приведенном решении. Вычислять 453 не требуется.
10 класс
1. Придумайте такое нецелое число, что 15% и 33% от него – целые числа.
Ответ. Например, 100/3.
2. Найдите сумму: 1002–992+982–972+…+22–12.
Решение.
По формуле разности квадратов 1002–992 = 100+99; 982–972=98+97; …
Поэтому 1002–992+982–972+…+22–12 = 100+99+98+97+96+95+..+2+1=(100+1)*100/2=5050.
Комментарий. Возможны и другие способы подсчета.
3. Встретились несколько друзей. Каждый из них обменялся рукопожатием с каждым, кроме Федота Бурчеева, который, будучи не в духе, некоторым пожал руку, а некоторым – нет.
Всего было сделано 197 рукопожатий. Сколько рукопожатий сделал Федот?
Ответ. 7 рукопожатий.
Решение. Если каждый из n человек пожмет руки всем остальным, то все сделают по n-1 рукопожатий, а всего рукопожатий будет сделано n(n-1)/2, ибо в каждом из них
участвуют двое. Посмотрим, сколько могло быть людей, кроме Федота. Заметим, что если 20 человек пожмут руки друг другу, то всего будет сделано 190 рукопожатий. Т.е. Федоту останется сделать 7 рукопожатий. Если же без Федота было менее 20 человек, то они сделали без него не более 19*18/2=171 рукопожатие, т.е. на долю Федота осталось бы не менее 26 рукопожатий, а человек, кому он мог бы пожать руку – не более 19 – противоречие. Если же без Федота было больше 20 человек, то только они одни в сумме сделали бы больше 197 рукопожатий (21*20/2=210>197). Таким образом, ответ единственный – Федот сделал 7 рукопожатий.
4. На круглой арене цирка (но не в ее центре) стоит тумба, на которой сидит лев. По команде укротителя лев спрыгивает с тумбы и бежит по прямой. Добежав до бортика, он поворачивает на 90градусов, снова добегает до бортика, поворачивает на 90градусов и т.д. Докажите, что на арене (но не на тумбе) можно положить кусочек мяса так, что, независимо от первоначального направления движения, лев съест мясо. (Лев съедает мясо, если его путь проходит через точку, в которой оно лежит.)
Ответ. Мясо надо положить в точку, симметричную тумбе относительно центра окружности.
Решение. Пусть тумба находится в точке T. Тогда лев движется вдоль ломаной TABC (см. рисунок). Продолжим AT до пересечения с окружностью в точке D. Так как хорды ВС и АD перпендикулярны хорде АВ, они симметричны относительно центра окружности. (Действительно, АС – диаметр, т.к. он виден из точки В под прямым углом. Аналогично ВD диаметр. Значит, точка их пересечения – центр окружности и центр симметрии прямоугольника ABCD.) Следовательно, независимо от начального направления, лев пройдет через точку U, симметричную точке T относительно центра окружности.
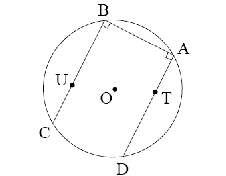
5. У каждого трехзначного числа нашли произведение его цифр. Получилось 900 произведений от 1*0*0 до 9*9*9 . Чему равна их сумма?
Ответ. 453=91125.
Решение. Достаточно заметить, что если мы раскроем скобки в произведении (1+2+…+9)·(0+1+2+…+9) ·(0+1+2+…+9), то получим как раз 900 перечисленных в условии слагаемых, а все три суммы, стоящие в скобках, равны 45.
6. Был квадратный трехчлен x2+10x+12. За один ход разрешается менять на единицу свободный член или коэффициент при x. После нескольких таких операций получили трехчлен x2+12x+10. Докажите, что в некоторый момент был трехчлен с целым корнем.
Решение. Заметим, что -1 является корнем квадратного трехчлена x2+(n+1)x+n, т.е. приведенного трехчлена, у которого коэффициент при x на 1 больше свободного члена. В изначальном трехчлене коэффициент при x меньше свободного члена, а в конечном – больше. А так как изменять мы можем только один из них на единицу, значит, в некоторый момент коэффициент при x был на 1 больше.
Комментарии по проверке
Каждая задача оценивается из 7 баллов. Каждая оценка – целое число от 0 до 7.
При оценке решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) – тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.
Задача 1. Правильный пример – 7 баллов.
Задача 2. Только ответ без обоснования, как он найден, – 2 балла. За представление выражения в виде суммы арифметической прогрессии – 2 балла. После этого арифметическая ошибка (но не
ошибка при подсчете количества слагаемых/пар и не ошибка в формуле, которые арифметическими не считаются) – 5 баллов.
Задача 3. Только ответ «7» без обоснования – 1 балл. Ответ с проверкой – 3 балла.
Задача 4. Ответ: «мясо нужно положить в точку, симметричную тумбе относительно центра арены», без достаточных обоснований, почему она годится – 3 балла.
Задача 5. За ответ без обоснования – 3 балла. С другой стороны, не надо требовать более подробного обоснования, чем в приведенном решении. Вычислять 453 не требуется, если такое вычисление есть и в нем допущена ошибка, оценка не снижается.
Задача 6. Сказано, что обязательно будет корень -1, но не сказано почему – 2 балла.
11 класс
1. Придумайте такое нецелое число, что 15% и 33% от него – целые числа.
Ответ. Например, 100/3.
2. Найдите сумму: 1002–992+982–972+…+22–12.
Решение.
По формуле разности квадратов 1002–992 = 100+99; 982–972=98+97; …
Поэтому 1002–992+982–972+…+22–12 = 100+99+98+97+96+95+..+2+1=(100+1)*100/2=5050.
Комментарий. Возможны и другие способы подсчета.
3. Встретились несколько друзей. Каждый из них обменялся рукопожатием с каждым, кроме Федота Бурчеева, который, будучи не в духе, некоторым пожал руку, а некоторым – нет.
Всего было сделано 197 рукопожатий. Сколько рукопожатий сделал Федот?
Ответ. 7 рукопожатий.
Решение. Если каждый из n человек пожмет руки всем остальным, то все сделают по n-1 рукопожатий, а всего рукопожатий будет сделано n(n-1)/2, ибо в каждом из них
участвуют двое. Посмотрим, сколько могло быть людей, кроме Федота. Заметим, что если 20 человек пожмут руки друг другу, то всего будет сделано 190 рукопожатий. Т.е. Федоту останется сделать 7 рукопожатий. Если же без Федота было менее 20 человек, то они сделали без него не более 19*18/2=171 рукопожатие, т.е. на долю Федота осталось бы не менее 26 рукопожатий, а человек, кому он мог бы пожать руку – не более 19 – противоречие. Если же без Федота было больше 20 человек, то только они одни в сумме сделали бы больше 197 рукопожатий (21*20/2=210>197). Таким образом, ответ единственный – Федот сделал 7 рукопожатий.
4. Докажите, что для любых x и y справедливо неравенство: sinxcosy+1≥sinx+cosy
Решение. Преобразуем: sinx(cosy-1)+1-cosy≥0. Последнее неравенство всегда верно, ибо cosy, sinx≤1.
5. В четырехугольнике АВСD углы А и С – прямые. Из точек В и D опустили перпендикуляры на диагональ АC и получили соответственно точки M и N. Докажите, что AM=CN.
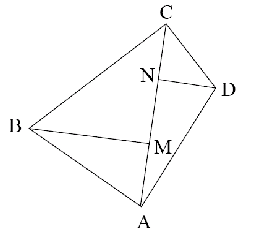
Решение. Треугольники BMC и CND – прямоугольные, при этом их острые углы BCN и DCN в сумме дают 90, следовательно
считая от точки А, а другая, считая от точки С. Значит, соответствующие отрезки AM и CN равны. Можно также вывести это явно: CM·NC =AN·MA => (AC-AM)NC=(AC-CN)MA =>
AC·NC =AC·MA =>NC=MA.
Второе решение. Обозначим середину отрезка NM через Q. Нетрудно видеть, что утверждение задачи равносильно тому, что Q – середина и отрезка AC. Заметим, что по теореме Фалеса точка Q есть основание перпендикуляра OQ, опущенного на CA из середины отрезка BD. Но, так как отрезок BD виден из точек A и C под прямыми углами, AC – хорда окружности с центром в точке O. А значит, OQ действительно делит отрезок AC пополам (как радиус, перпендикулярный хорде).
6. Существует ли одиннадцатигранник (не обязательно выпуклый), у которого каждая грань – многоугольник с четным числом сторон?
Ответ. Да, существует.
Решение.
Заметим, что если из куба вырезать кубик поменьше (оба куба имеют общий трехгранный угол) – см. рисунок 1, получится 9-гранник, у которого все грани – чётноугольники. А чтобы получился 11-гранник вместо большого куба возьмем шестиугольную призму – см. рисунок 2.
Другой пример. Рассмотрим многогранник в виде объемной буквы Т – см. рис.1. Срежем у него часть «ножки», как показано на рисунке 2. Получим 11-гранник, у которого нижняя грань
8-угольник, а остальные грани четырехугольные.
Комментарий. Кроме многогранников, изображенных на рис. 1.2 и 2.2 есть и другие примеры.
Комментарии по проверке
Каждая задача оценивается из 7 баллов. Каждая оценка – целое число от 0 до 7. При оценке
решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) – тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.
Задача 1. Правильный пример – 7 баллов.
Задача 2. Только ответ без обоснований, как он найден, – 2 балла.
За представление выражения в виде суммы арифметической прогрессии – 2 балла. После этого арифметическая ошибка (но не ошибка при подсчете количества слагаемых/пар или ошибка в
формуле, которые арифметическими не считаются) – 5 баллов.
Задача 3. Только ответ «7» без обоснования – 1 балл. Ответ с проверкой – 3 балла.
Задача 6. Ответ «Да» – 0 баллов. У многогранника могут быть грани, являющиеся «многоугольниками с дырками», оценка за это не снижается.