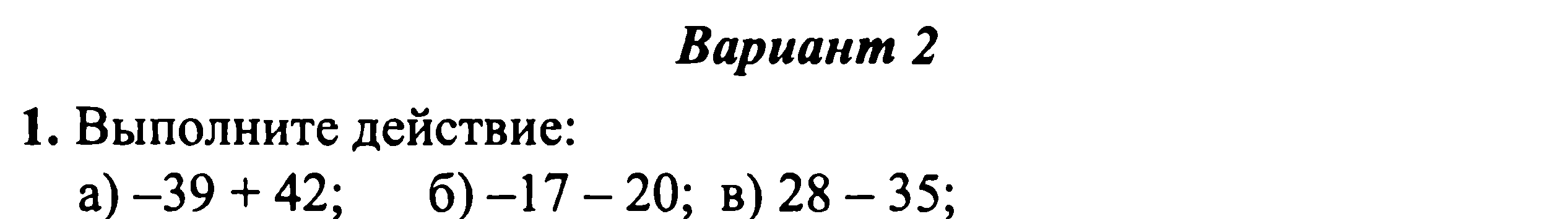Правила в таблицах по математике 6 класс: 5-6 – 19 photos | VK – Справочные таблицы по математике 6 класс скачать

Опорная таблица по курсу математики 6 класса.

Опорная таблица по курсу математики 6 класса.

Делителем натурального числа a называют натуральное число, на которое a делится без остатка.

Число 12 имеет шесть делителей: 1, 2, 3, 4, 6 и 12.

Кратным натурального числа a называют натуральное число, делится без остатка на a.

Первые пять чисел, кратных 8: 8, 16,24, 32, 40.

Признаки делимости

На 2

Если запись натурального числа оканчивается четной цифрой, то это число четно (делится без остатка на 2), а если запись числа оканчивается нечетной цифрой, то это число нечетно.

На 3

Если сумма цифр числа делится на 3, то и число делится на 3.

На 5

Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.

На 9

Если сумма цифр числа делится на 9, то и число делится на 9.

На 10

Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.

Число, делящееся только на 1 и само на себя – простое число.

Число, имеющее более двух делителей – составное число.

Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел (НОД).

Чтобы найти НОД нескольких натуральных чисел, надо:

1) Разложить их на простые множители;

2) Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;

3) Найти произведение оставшихся множителей.

Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.

Наименьшим общим кратным натуральных чисел a и b называют наименьшее натуральное число, которое кратно и a, и b (НОК).

Чтобы найти НОК нескольких натуральных чисел, надо:

1) Разложить их на простые множители;

2) Выписать множители, входящие в разложение одного из этих чисел;

3) Добавить к ним недостающие множители из разложений остальных чисел;

4) Найти произведение получившихся множителей.

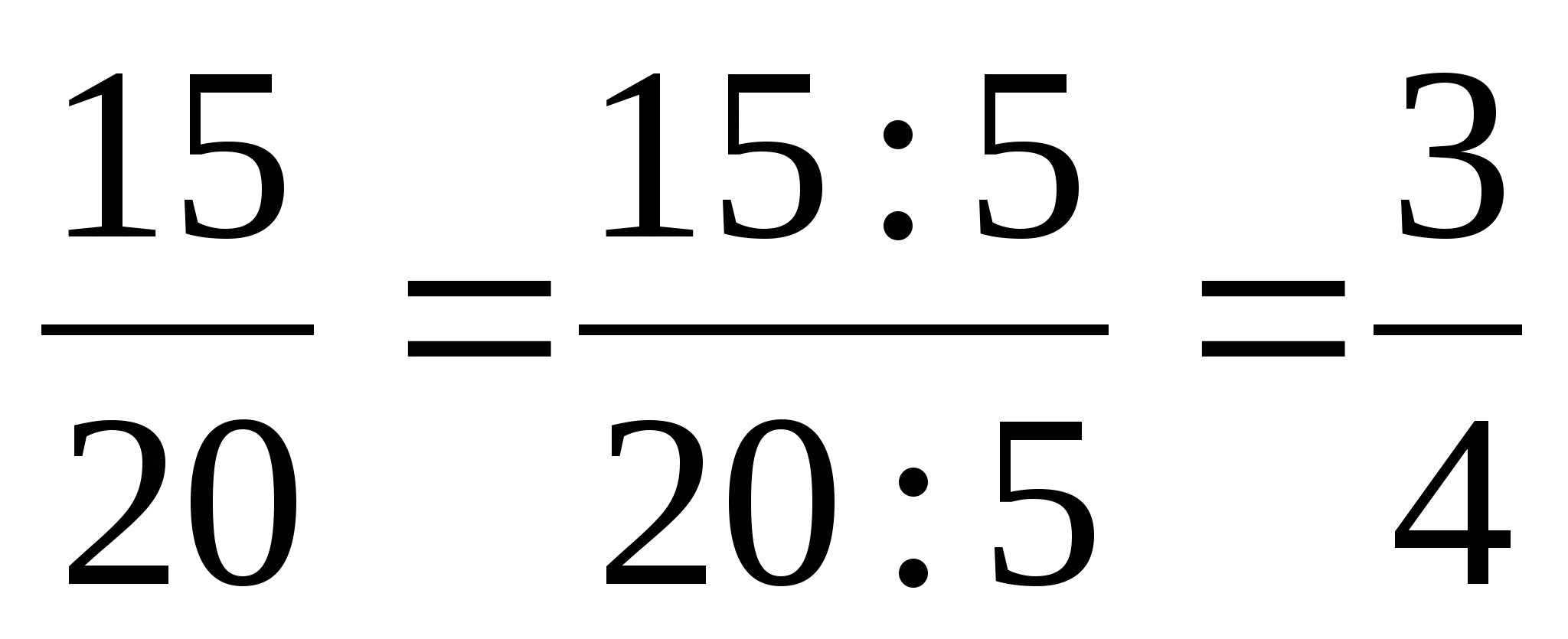
Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

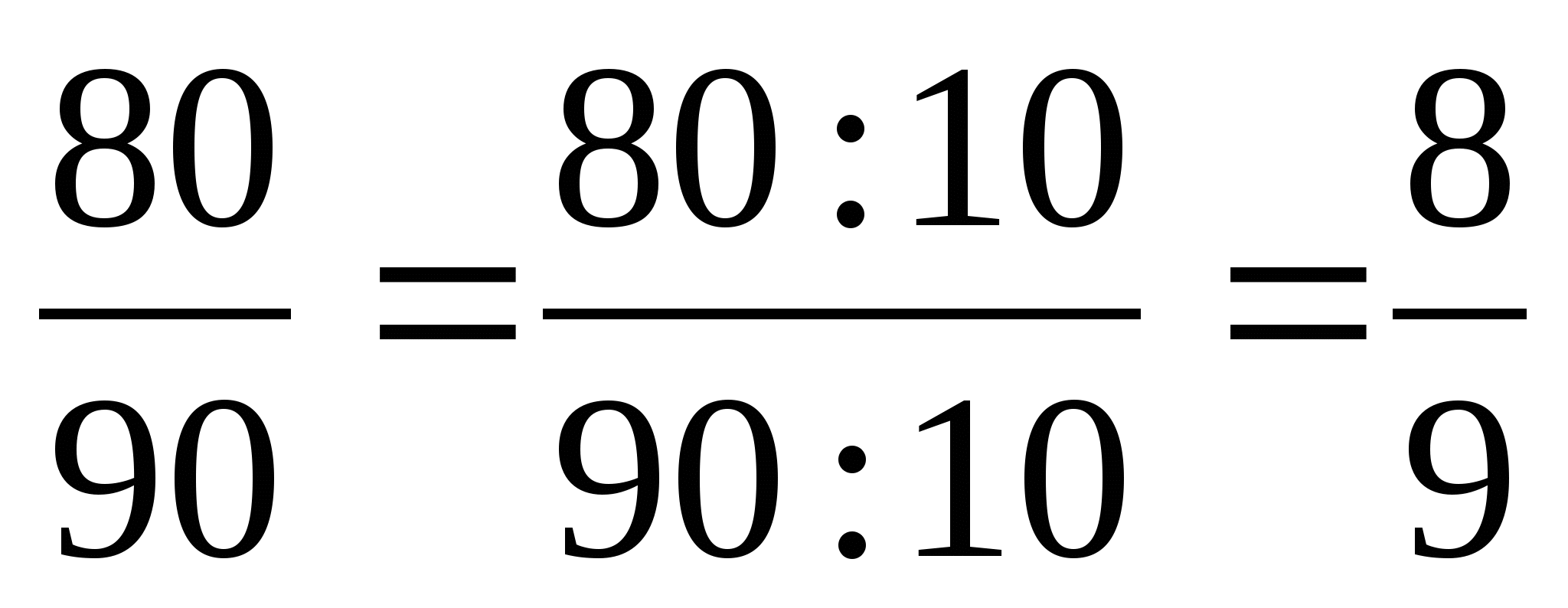
Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроб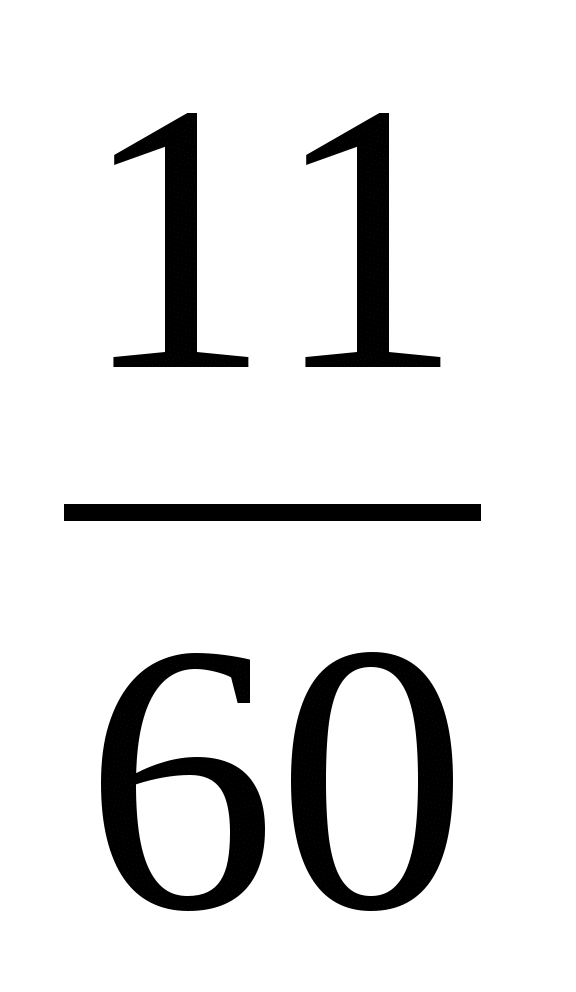и.

и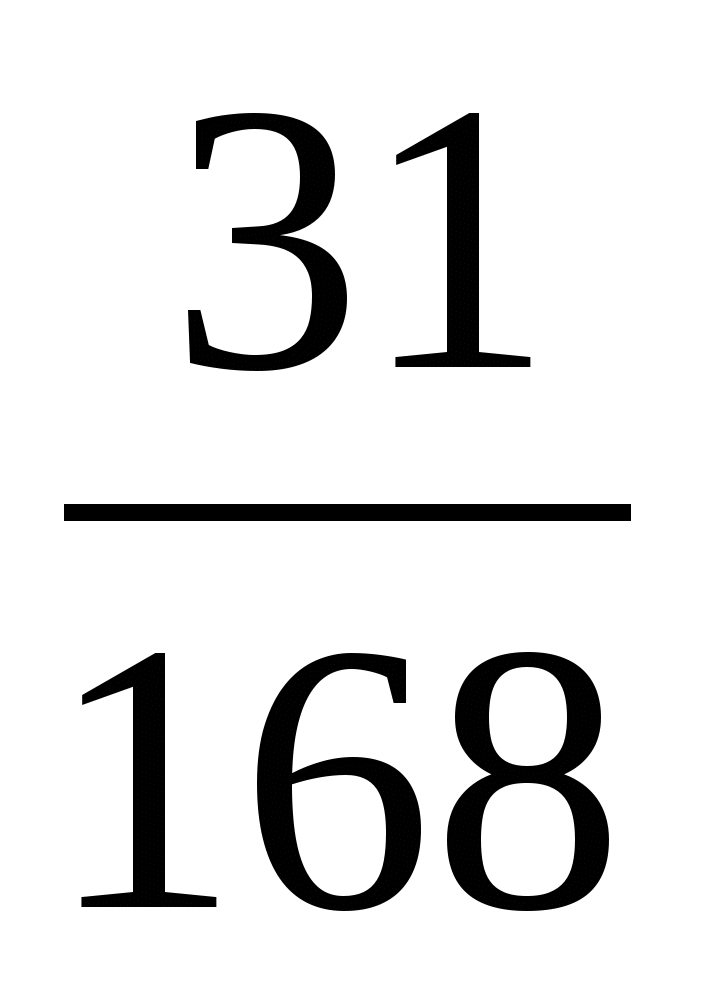

60 = 2 · 2 · 3 · 5

168 = 2 · 2 · 2 · 3 · 7

Наименьший общий знаменатель:

2 · 2 · 2 · 3 · ·5 · 7 = 840

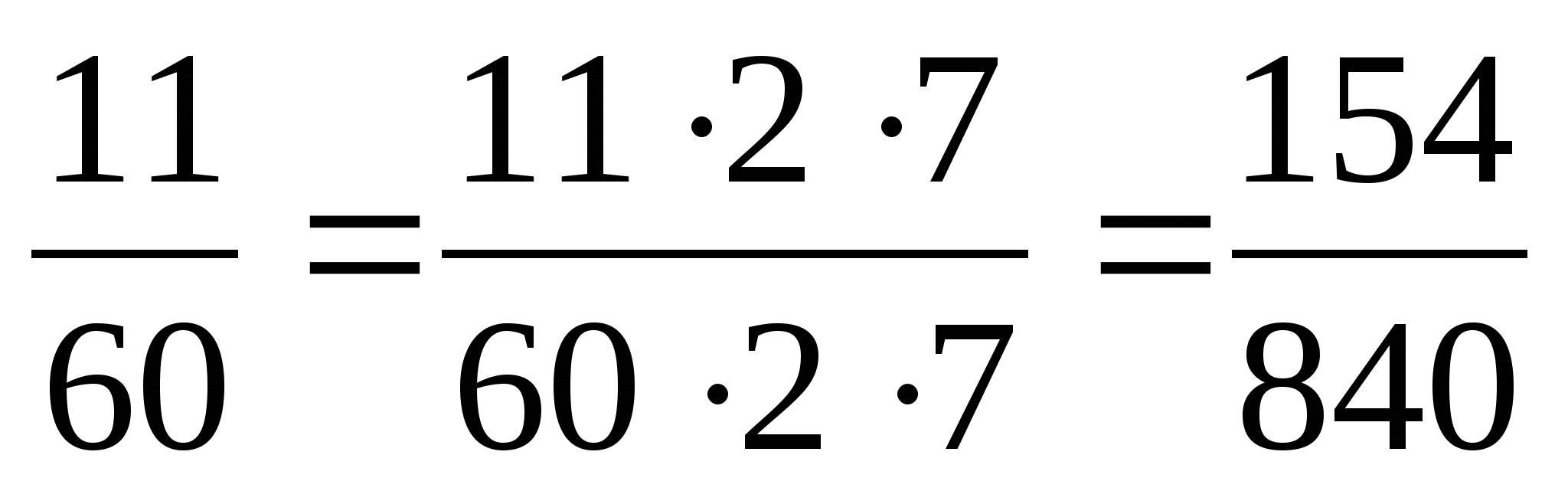
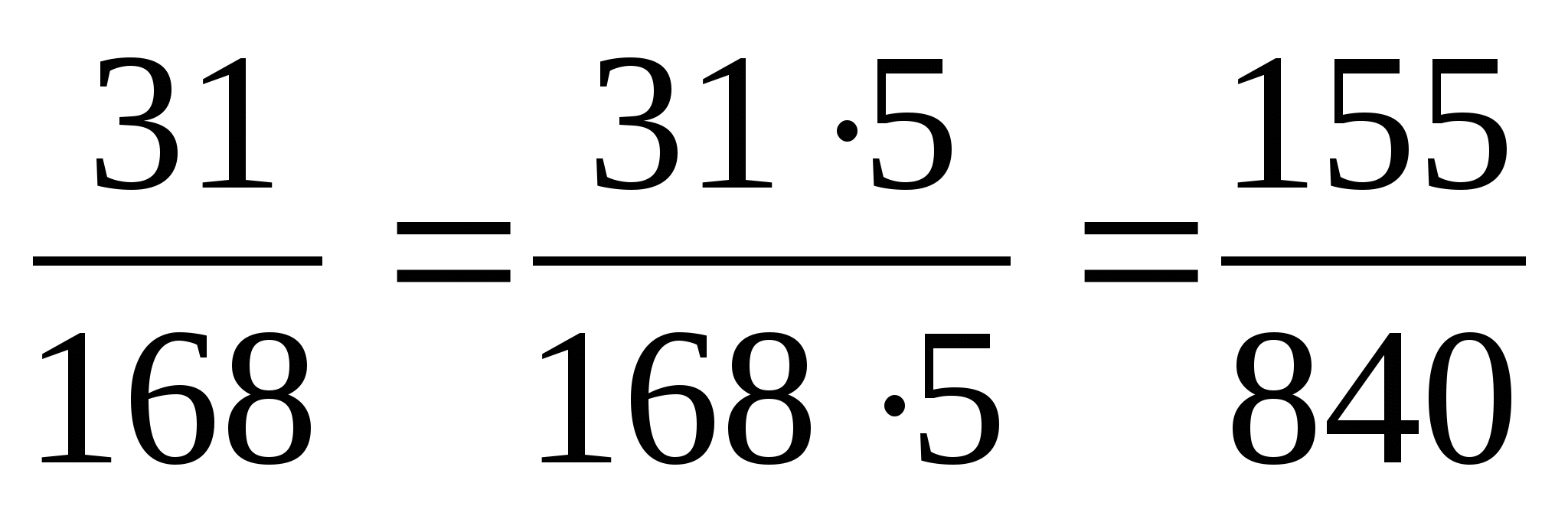
Чтобы привести дроби к наименьшему общему знаменателю, надо:

1) Найти НОК знаменателей этих дробей, оно и будет наименьшим общим знаменателем;

2) Разделить наименьший общий знаменатель на знаменатели этих дробей, т. е. найти для каждой дроби дополнительный множитель;

3) Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Чтобы сравнить (сложить, вычесть) дроби с разными знаменателями, надо:

1.) Привести данные дроби к наименьшему общему знаменателю;

2.) Сравнить (сложить, вычесть) полученные дроби.

5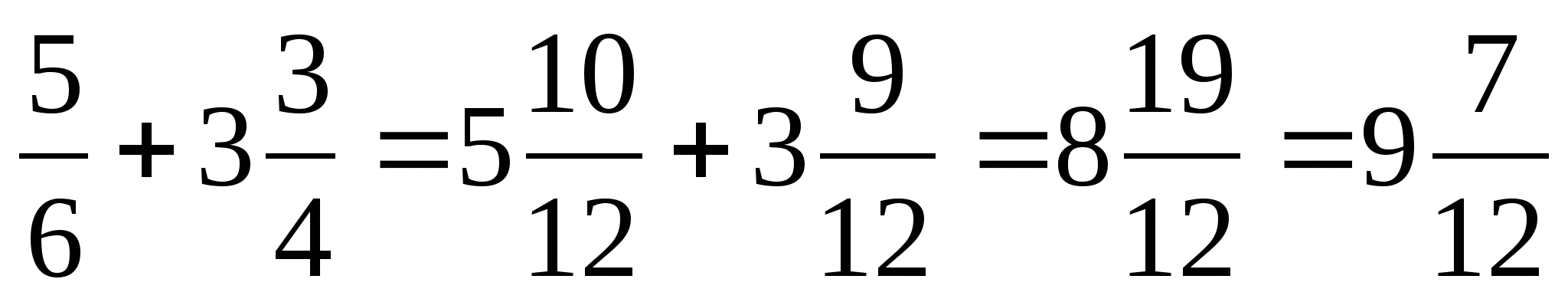

Чтобы сложить смешанные числа, надо:

1) Привести дробные части этих чисел к наименьшему общему знаменателю;

2) Отдельно выполнить сложение целых частей и отдельно – дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части.

3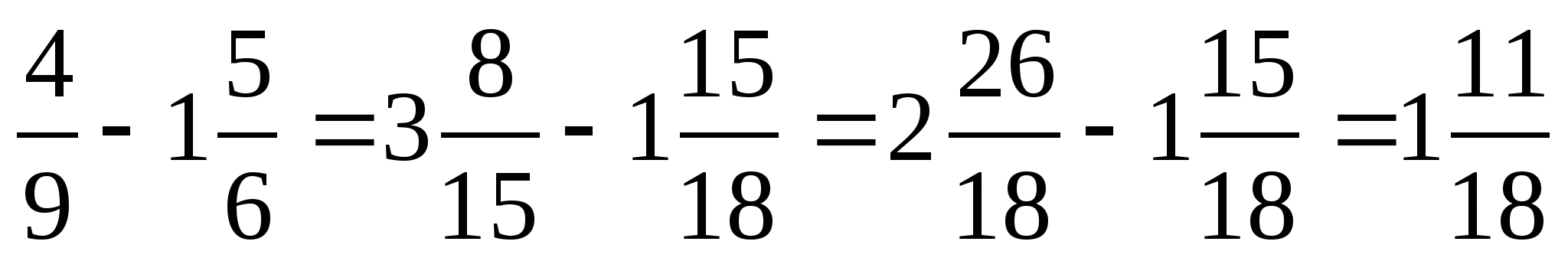

Чтобы выполнить вычитание смешанных чисел, надо:

1) Привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу целую часть;

2) Отдельно выполнить вычитание целых частей и отдельно дробных частей.

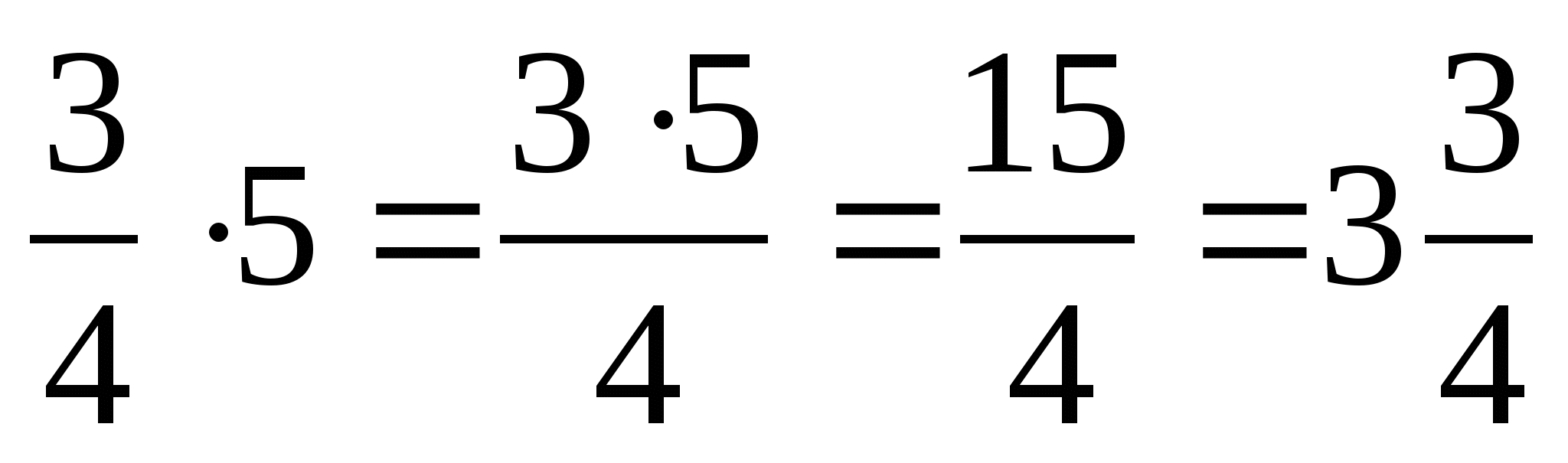
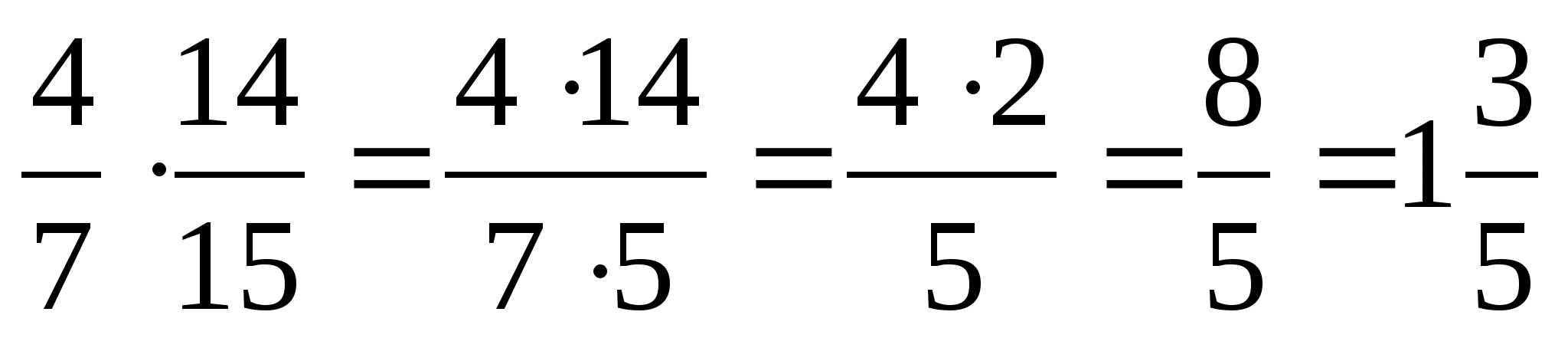
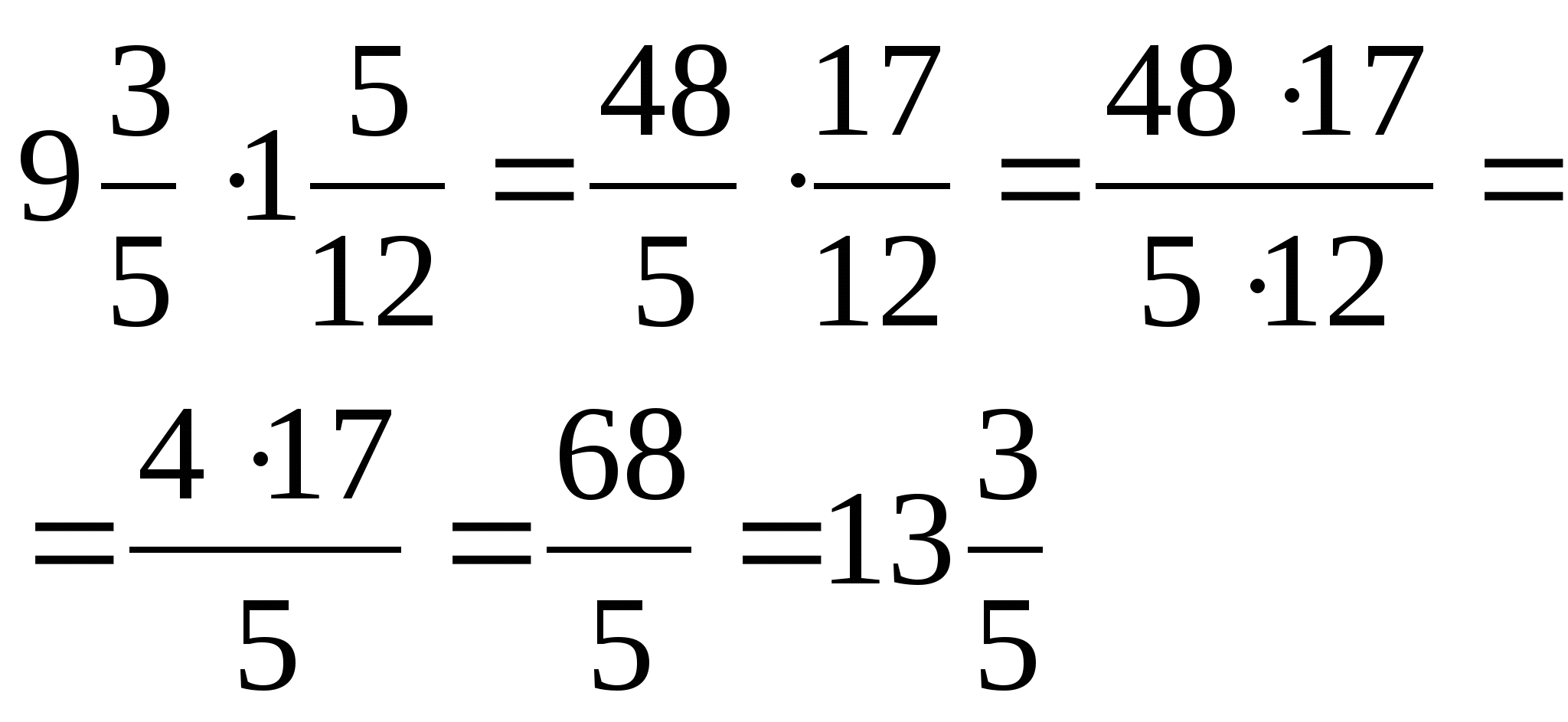
Чтобы умножить дробь на натуральное число, надо ее числитель умножить это число, а знаменатель оставить без изменения.

Чтобы умножить дробь на дробь, надо:

1) Найти произведение числителей и произведение знаменателей этих дробей;

2.) Первое произведение записать числителем, а второе – знаменателем.

Чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

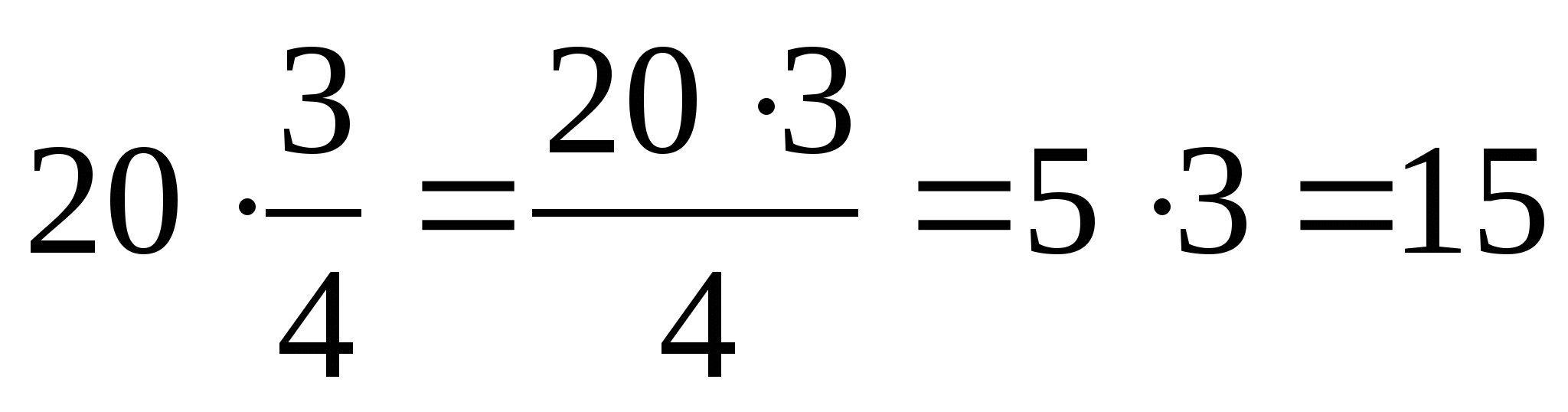
Чтобы найти дробь от числа, нужно умножить число на эту дробь.

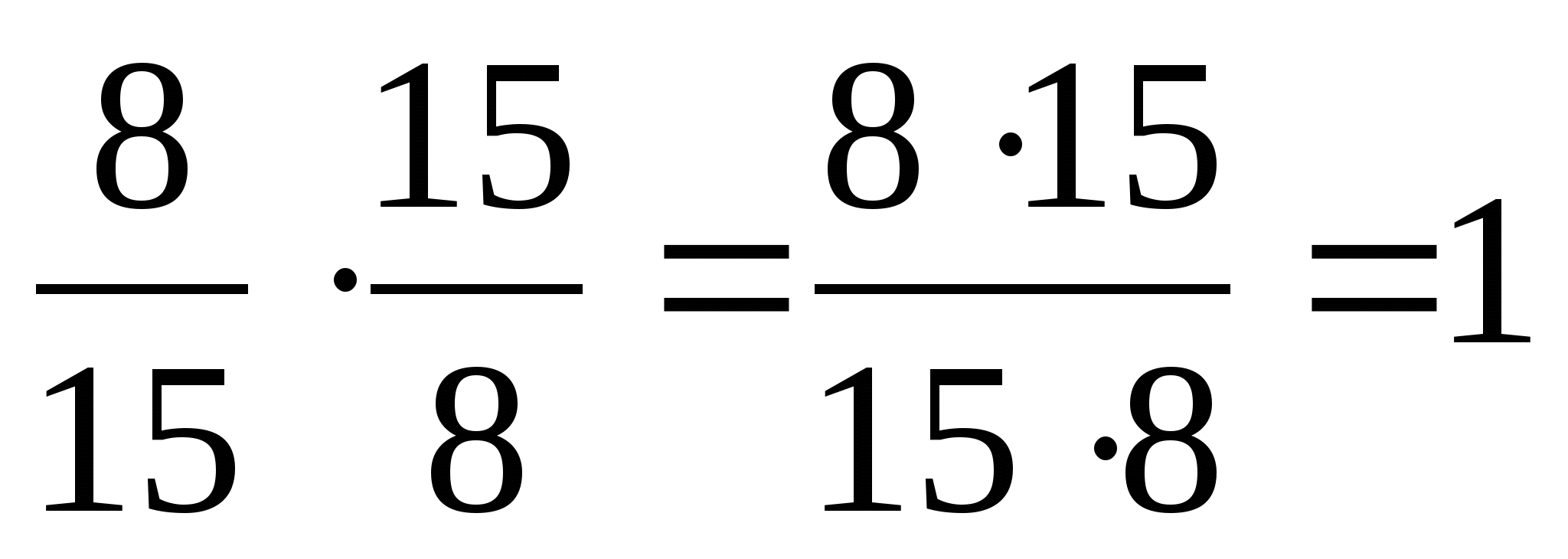
Два числа, произведение которых равно 1, называют взаимно обратными.

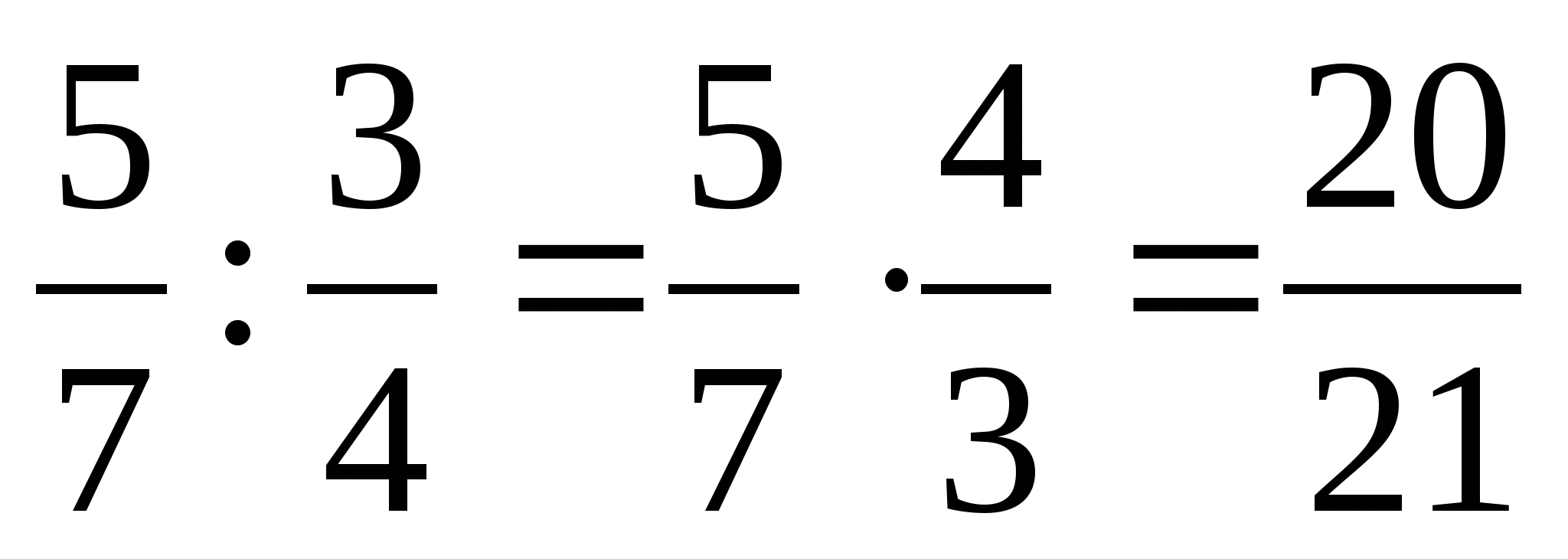
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.

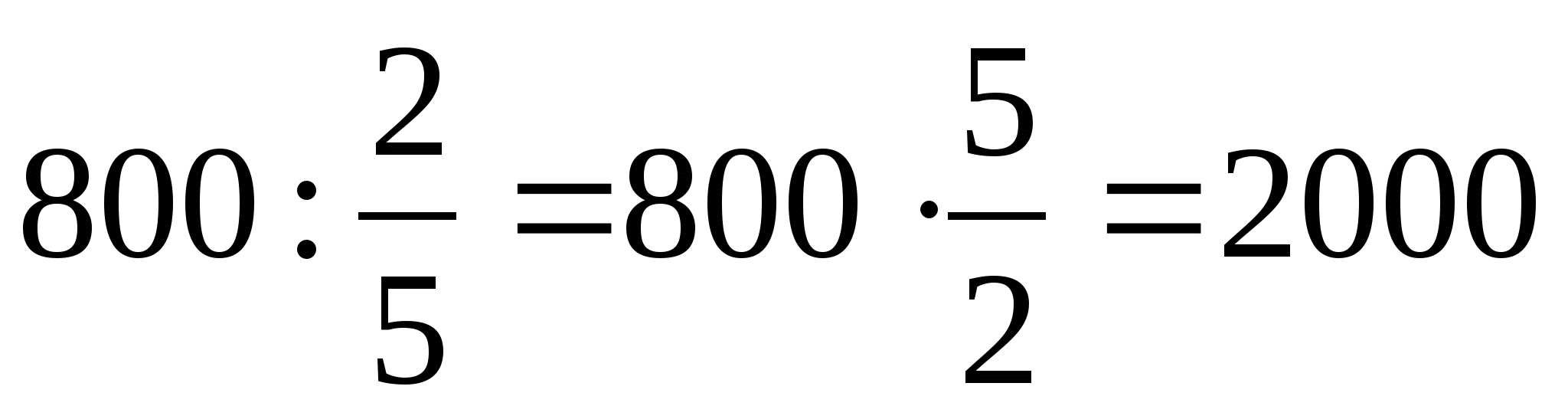
Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.

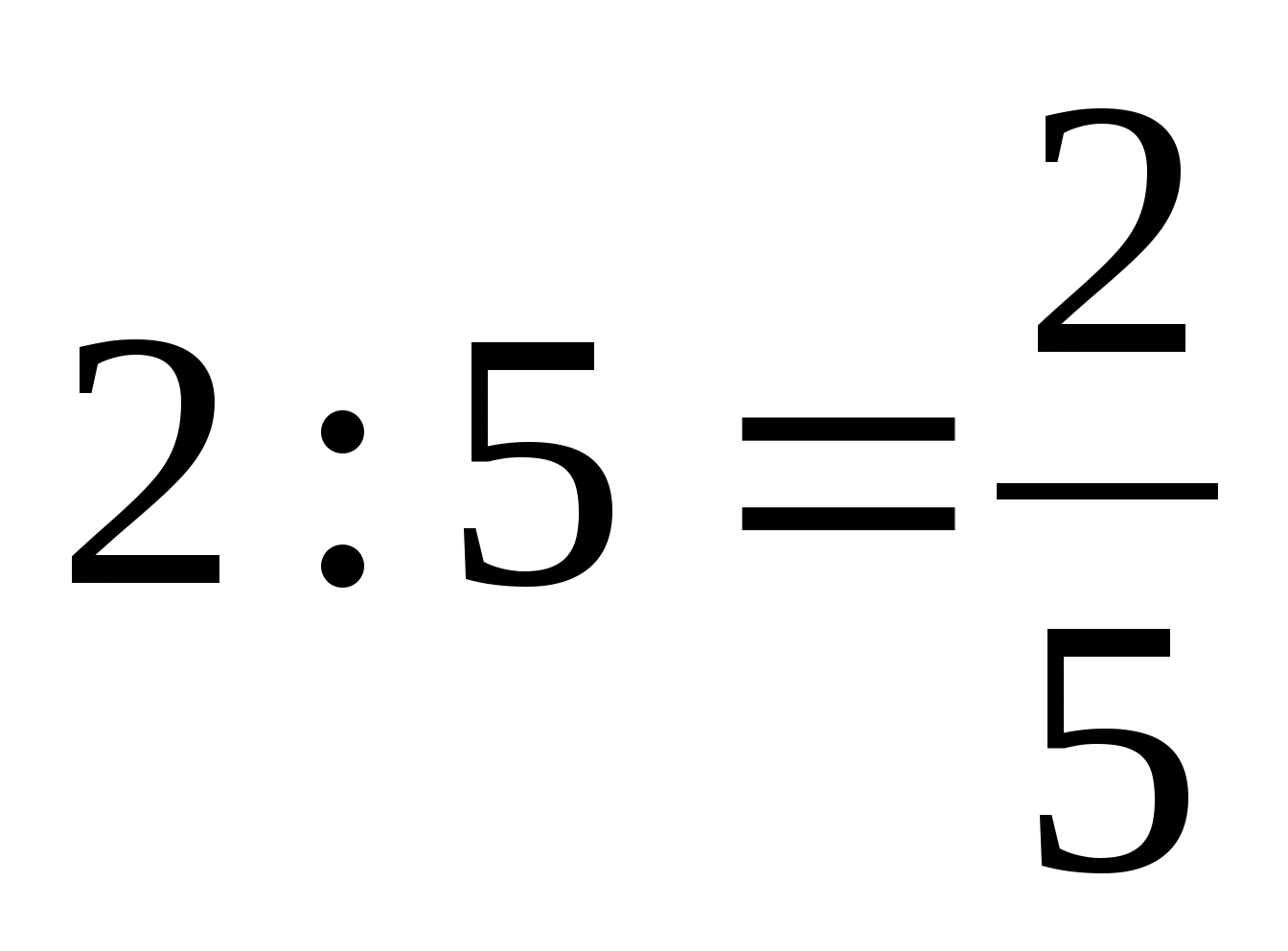
Частное двух чисел называют отношением этих чисел. Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.

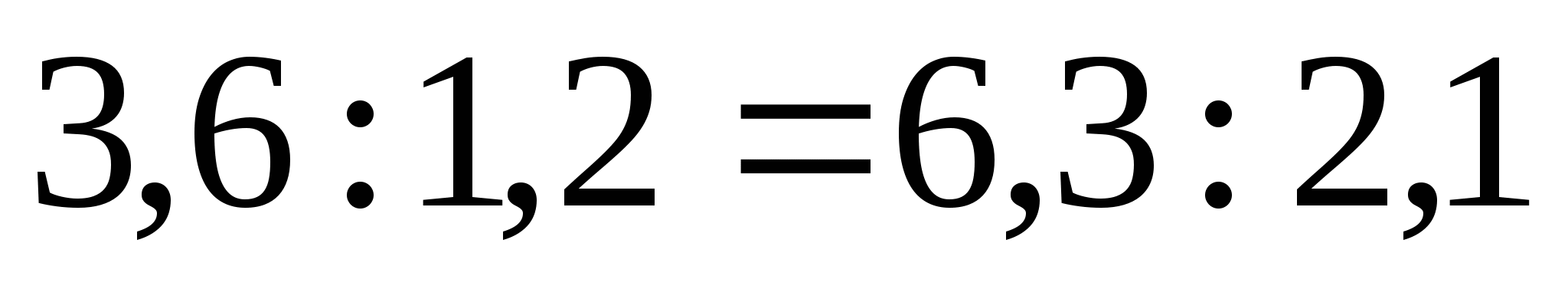или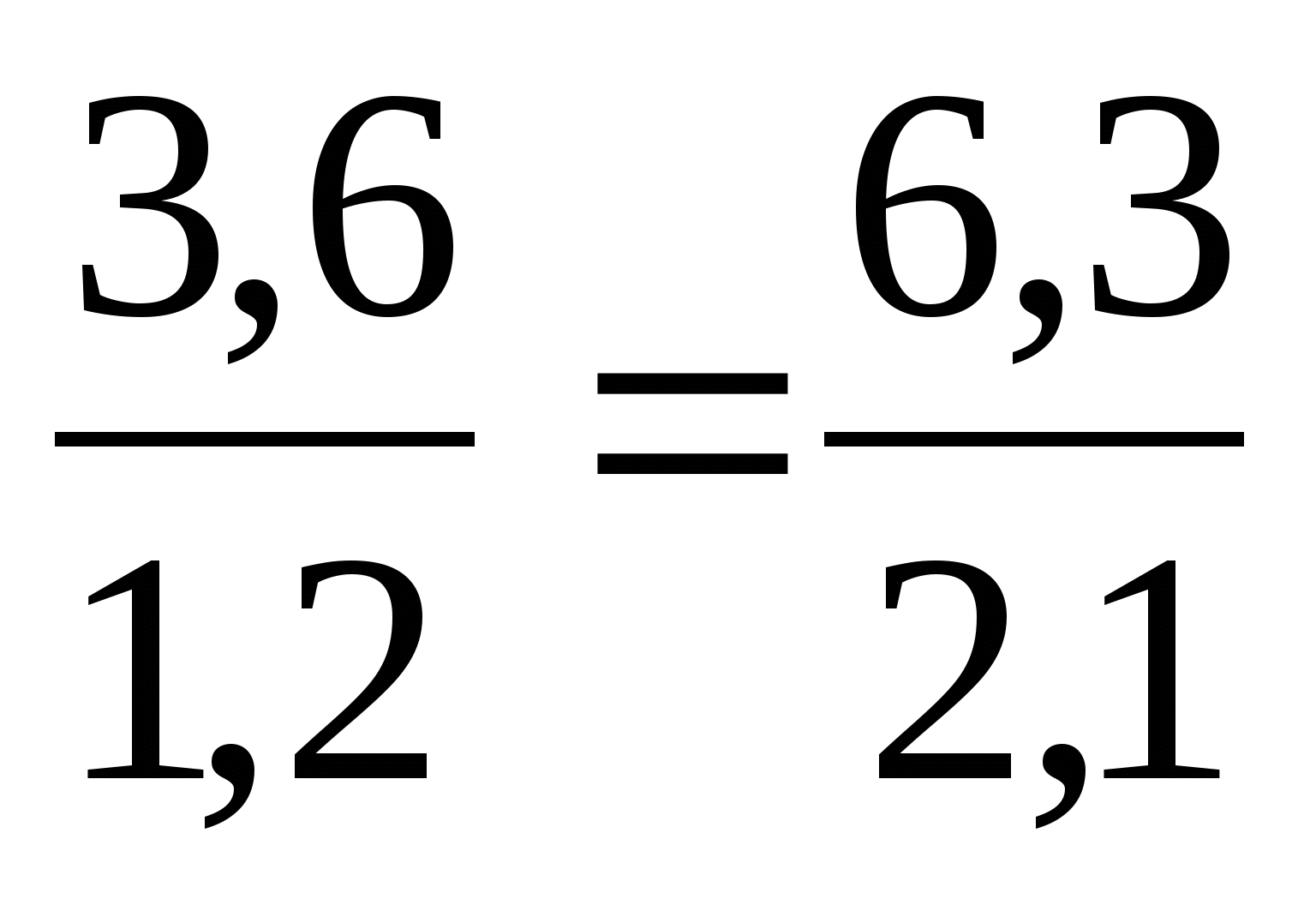

a:b=c:d

a·d=b·c

Равенство двух отношений называют пропорцией.

Числа a и d – крайние члены пропорции; b и с – средние

В верной пропорции произведение крайних членов равно произведению средних.

Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна.

4 : 2 = 56 : 28

7 : 21 = 15 : 45

5 : 25 = 7 : 35

Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.

Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.

Если две величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины.

Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.

1: 100000 = 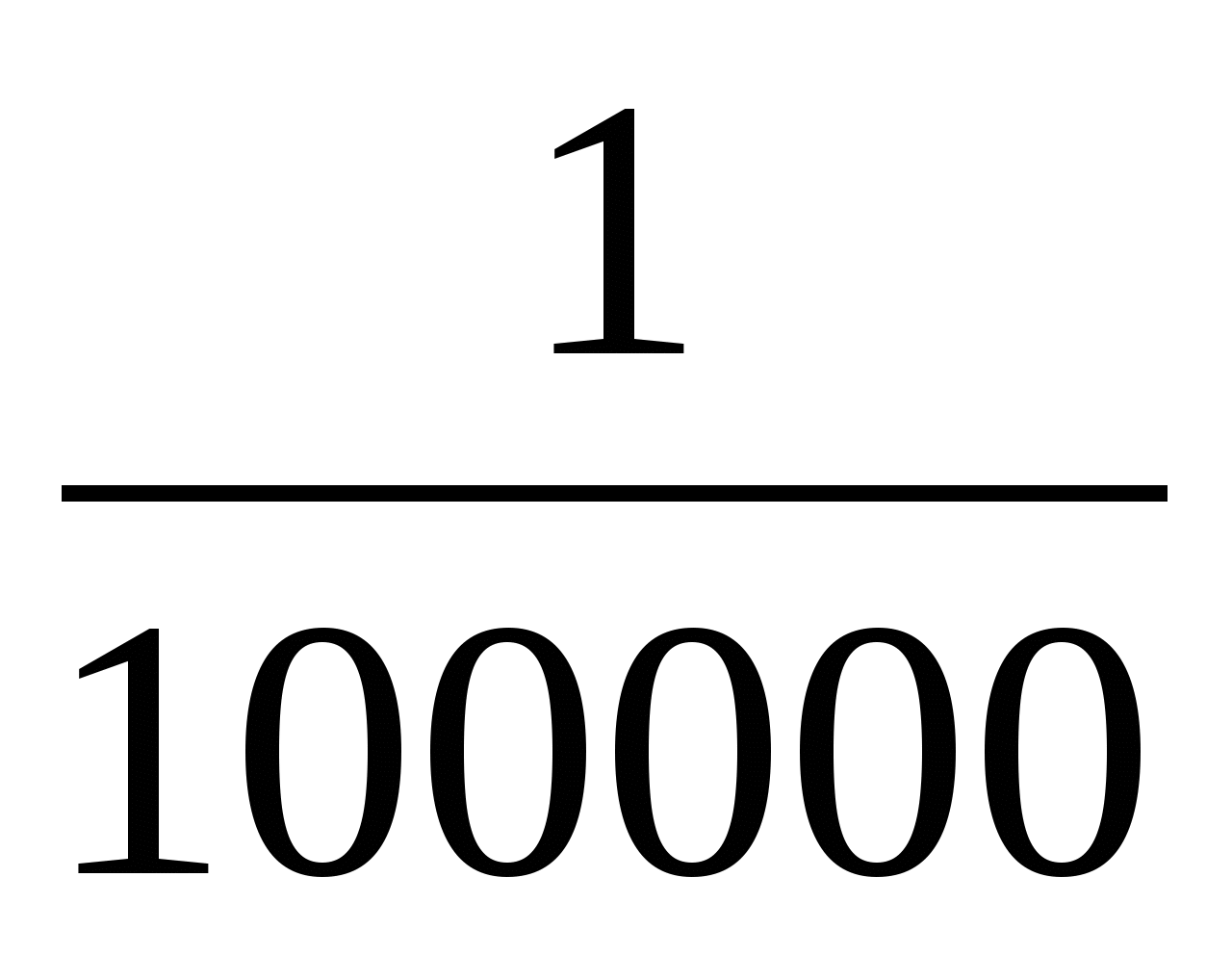– карта выполнена в масштабе одна стотысячная

C = 2·π·r

Длина окружности

r – радиус окружности

π = 3,14

S = π·r²

Площадь круга

r – радиус окружности

π = 3,14

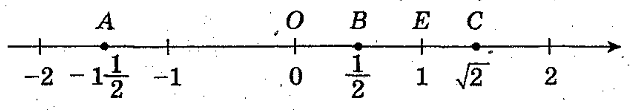
Прямую, с выбранными на ней началом отсчета, единичным отрезком и направлением называют координатной прямой.

Число, показывающее положение точки на прямой, называют координатой этой точки.

2,6 и -2,6

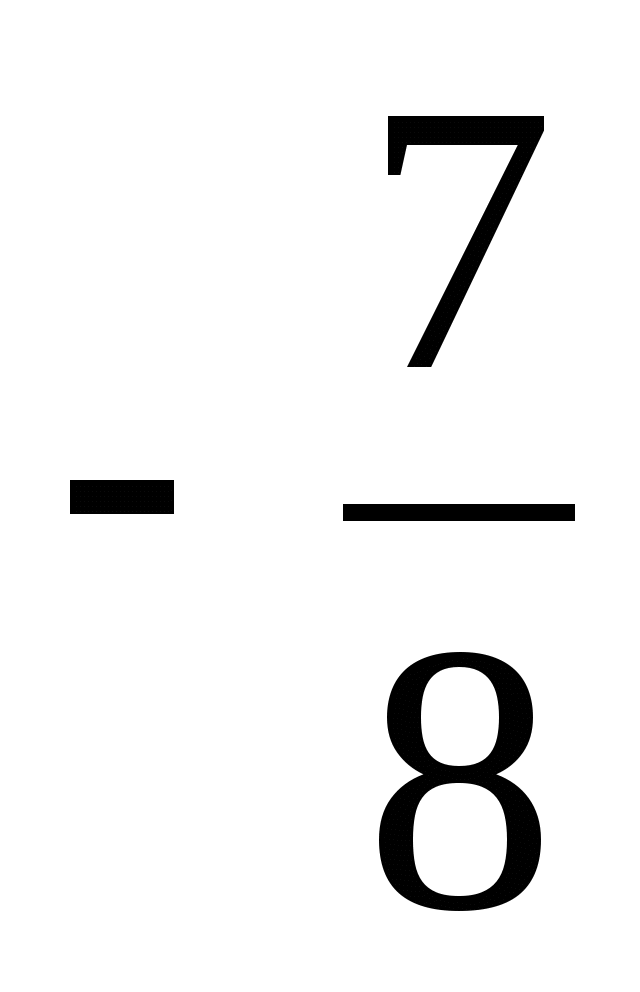и

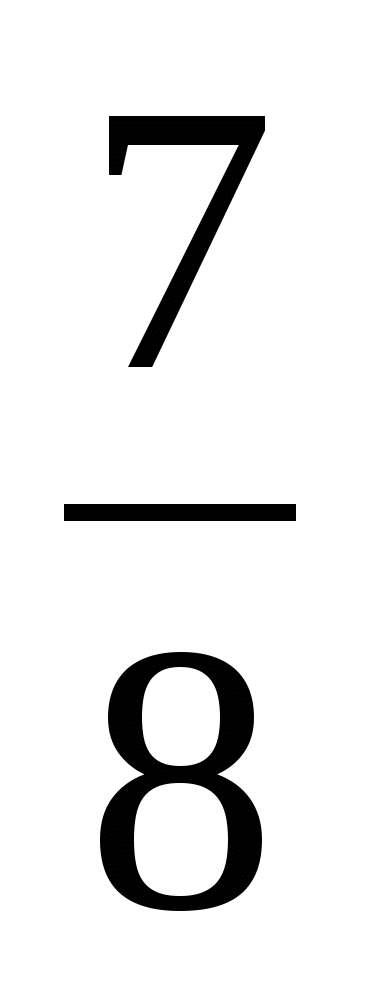
Два числа, отличающиеся друг от друга только знаками, называют противоположными числами.

Натуральные числа, противоположные им числа и нуль называют целыми числами.

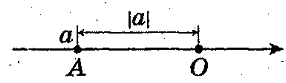
Модулем числа a (|a|) называют расстояние (в единичных отрезках) от начала координат до точки А (а).

– 8,7 + (– 3,5) = – (8,7 + 3,5) = – 12,2

Чтобы сложить два отрицательных числа, надо:

1) Сложить их модули;

2) Поставить перед полученным числом знак –.

6,1 + (– 4,2) = + (6,1 – 4,2) = 1,9

или

6,1 + (– 4,2) = 6,1 – 4,2 = 1,9

Чтобы сложить два числа с разными знаками, надо:

1) Из большего модуля слагаемых вычесть меньший;

2) Поставить перед полученным числом знак того слагаемого, модуль которого больше.

Если A(9) и В(– 5), то |AB|=9 – (– 5)= 14

Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.

(–1,2)·0,3 = –(1,2·0,3) = –0,36

Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным числом знак –.

(–3,2)·( –9) = |–3,2|·|–9|=3,2·9=28,8

Чтобы перемножить два отрицательных числа, надо перемножить их модули.

(–12) : ( –4) = 12 : 4 = 3

Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.

3,6 : (–3) = –(3,6:3) = –1,2

При деление чисел с разными знаками, надо:

1) Разделить модуль делимого на модуль делителя.

2) Поставить перед полученным числом знак.

x =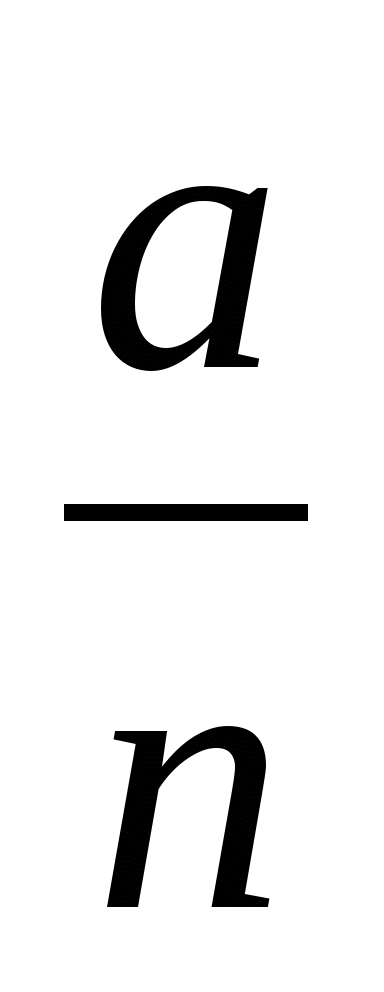

Число x, которое можно записать в виде отношения 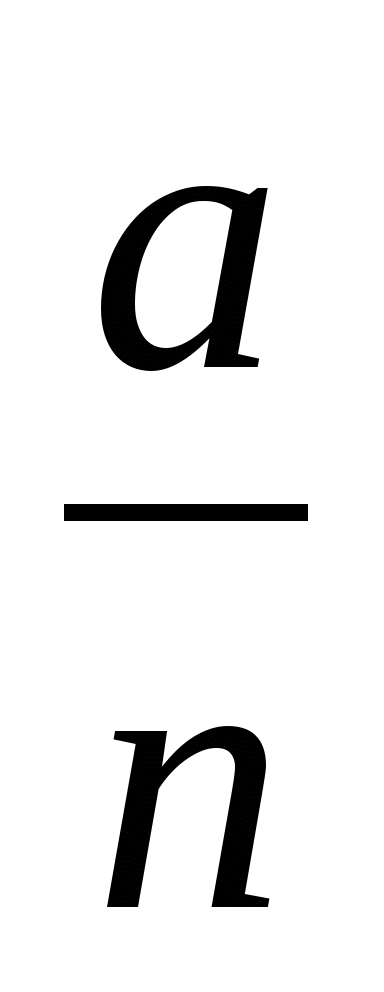, где a – целое число, а n – натуральное число, называют рациональным числом.

16–(10–18+12) = 16+(–(10–18+12))=16+(–10+18–12) = 16–10+18–12=12

Чтобы раскрыть скобки, перед которыми стоит знак –, надо заменить этот знак на +, поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.

0,3a·(–0,7b) = 0,3·a·(–0,7)·b = (0,3·(–0,7))·(a·b) = –0,21ab; –0,21 – коэффициент

Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом (или просто коэффициентом).

2m – 7m + 3m = m·(2–7+3) = –2m

Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.

Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.

Свойства уравнений

1.) Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.

2.) Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.

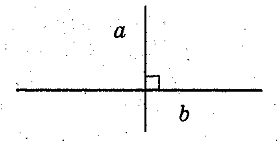
Две прямые, образующие при пересечении прямые углы, называют перпендикулярными ().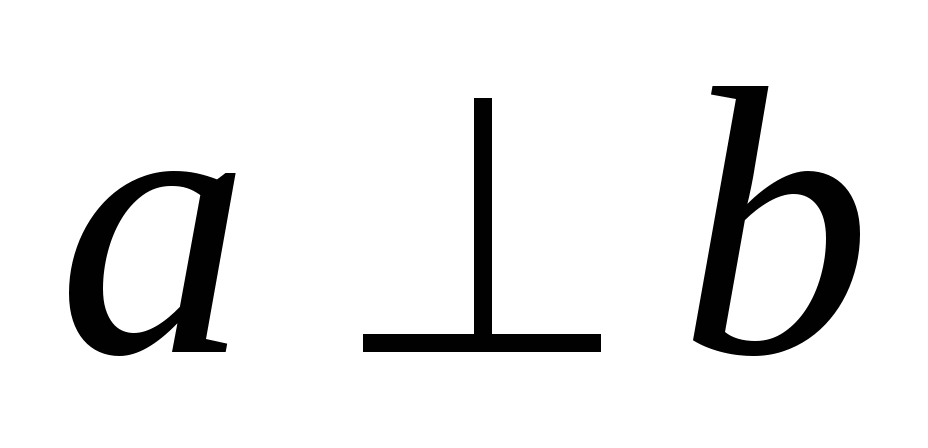

Две непересекающиеся прямые на плоскости называют параллельными ().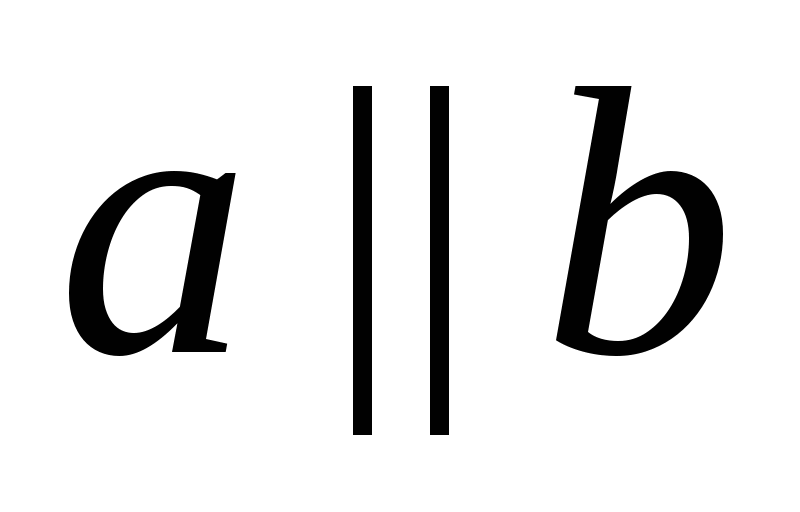

Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны.

Через каждую точку плоскости, не лежащую на данной прямой можно провести только одну прямую, параллельную данной прямой.

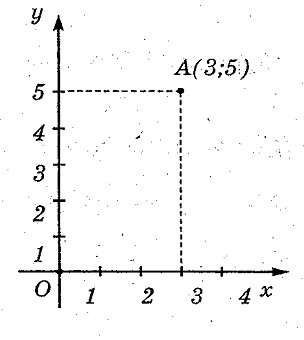
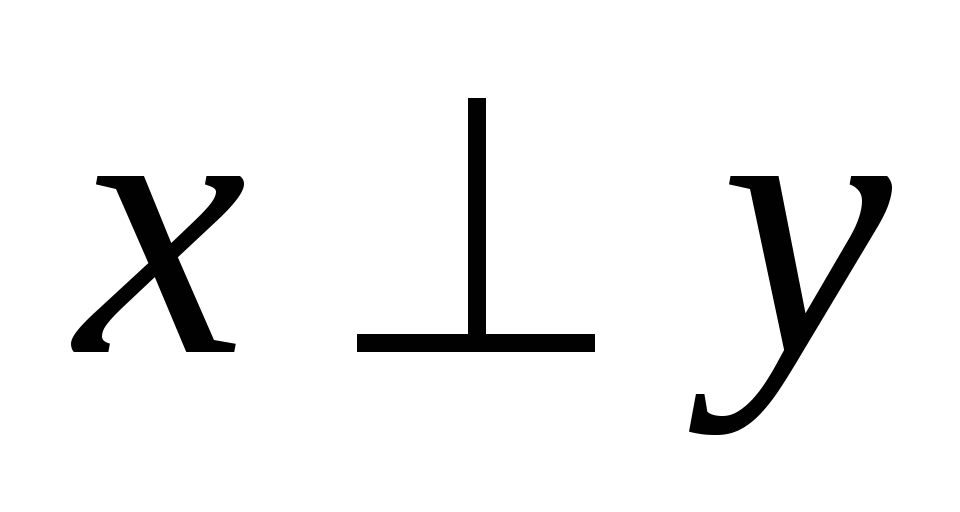– система координат на плоскости

О – начало координат, x – ось абсцисс, y – ось ординат

(3;5) – координаты точки А

Справочные таблицы по математике 6 класс — К уроку — Математика, алгебра, геометрия

Делители и кратные 6кл.М.01

Делителем натурального числа а называется натуральное число, на которое а делится без остатка.
Кратным натурального числа а называют натуральное число , которое делится без остатка на а.
Любое натуральное число имеет бесконечно много кратных.

Признаки делимости

Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.
Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.
Если запись натурального числа оканчивается чётной цифрой, то это число делится без остатка на 2.
Если сумма цифр числа делится на 9, то и число делится на 9.
Если сумма цифр числа делится на 3, то и число делится на 3

НОД и НОК 6кл.М.02
Натуральное число называют простым, если оно имеет только два делителя: единицу и само это число.
Натуральное число называют составным, если оно имеет более двух делителей.
Наибольшее натуральное число, на которое делятся без остатка числа a и b , называют наибольшим общим делителем этих чисел. НОД(24;36)=12
Натуральные числа называют взаимно простыми, если наибольший общий делитель равен 1.
Чтобы найти НОД нескольких натуральных чисел , надо:
 Разложить их на простые множители;
 Из множителей , входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
 Найти произведение оставшихся множителей
Наименьшим общим кратным натуральных чисел a и b называют наименьшее натуральное число, которое кратно и a, и b.
Чтобы найти наименьшее общее кратное нескольких натуральных чисел , надо:
 Разложить их на простые множители;
 Выписать множители, входящие в разложение остальных чисел
 Добавить к ним недостающие множители из разложений остальных чисел
 Найти произведение получившихся множителей
НОД(24;36)= 2•2•3=12 НОК(24;36)=2•2•2•3•3=72
24 2 36 2 24 2 36 2
12 2 18 2 12 2 18 2
6 2 9 3 6 2 9 3
3 3 3 3 3 3 3 3
1 1 1 1
Сложение и вычитание дробей 6кл.М.03

с разными знаменателями

Чтобы сравнить(сложить, вычесть) дроби с разными знаменателями, надо:
 Привести данные дроби к наименьшему общему знаменателю;
 Сравнить (сложить, вычесть) полученные дроби

+ —
Чтобы сложить смешанные числа , надо:
 Привести дробные части этих чисел к наименьшему общему знаменателю;
 Отдельно выполнить сложение целых частей и отдельно – дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части


Чтобы выполнить вычитание смешанных чисел, надо:
 Привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть;
 Отдельно выполнить вычитание целых частей и отдельно дробных частей

Умножение и деление 6 кл.М.04
обыкновенных дробей
Чтобы умножить дробь на натуральное число, надо её числитель умножить на это число, а знаменатель оставить без изменения.
=
Чтобы умножить дробь на дробь, надо:
 Найти произведение числителей и знаменателей этих дробей;
 Первое произведение записать числителем, а второе – знаменателем.


Для того чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Чтобы найти дробь от числа , нужно умножить число на эту дробь.
Чтобы умножить смешанное число на натуральное число, можно:
 Умножить целую часть на натуральное число
 Умножить дробную часть на это натуральное число
 Сложить полученные результаты
Два числа, произведение которых равно 1, называют взаимно обратными.
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.

Чтобы найти число по данному значению его дроби, надо это значение разделить на эту дробь.
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.

Отношения и пропорции 6 кл.М.05
Частное двух чисел называют отношением этих чисел.
Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.
Равенство двух отношений называют пропорцией.
a÷b=c÷d
а и d — крайние члены пропорции, c и b- средние члены пропорции
В верной пропорции произведение крайних членов равно произведению средних.
a•d=b•c
Если произведение крайних членов пропорции равно произведению среднтх членов, то пропорция верна.
Чтобы найти неизвестный крайний член пропорции, надо произведение средних членов разделить на известный крайний член пропорции.
a=
Чтобы найти неизвестный средний член пропорции, надо произведение крайних членов пропорции разделить на известный средний член пропорции
d=
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.

Масштаб 6 кл.М.06

Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
М=

Длина окружности. Площадь круга.

C=2πr S =

C – длина окружности, r – радиус окружности
S – площадь круга

Шар

r- радиус шара
d – диаметр шара

Положительные и отрицательные числа 6 кл.М.07

Числа со знаком + называют положительными.
Числа со знаком — называют отрицательными.
Два числа, отличающиеся друг от друга только знаками, называют противоположными числами.
Натуральные числа, противоположные им числа и нуль называют целыми числами.
Модуль числа
Модулем числа а называют расстояние ( в единичных отрезках) от начала координат до точки А (а).
5 4
-5 0 4 х

а, если а ≥ 0
│а│=
-а, если а < 0

│0│=0
│4│=4
│-5│=5

Сложение и вычитание 6 кл.М.08
положительных и отрицательных чисел
Чтобы сложить два отрицательных числа, надо:
 Сложить их модули;
 Поставить перед полученным числом знак — .

-8,7+ (-3,5)= — ( 8,7 + 3,5 ) = — 12,2
-2

Чтобы сложить два числа с разными знаками, надо:
 Из большего модуля слагаемых вычесть меньший;
 Поставить перед полученным числом знак того слагаемого, модуль которого больше.

6,1 + ( -4,2 ) = + (6,1 – 4,2 ) = 1,9
— 8

Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому: a-b=a+(-b)

18 – 14 =- 18 + ( — 14) = — ( 18 + 14 )= — 32

Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.

Умножение и деление 6 кл.М.09
положительных и отрицательных чисел

Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным числом знак — .
( — 1,2 ) • 0,3 = — ( 1,2 • 0,3 ) = — 0,36
1,2 • ( — 0,3 ) = — ( 1,2 • 0,3 ) = — 0,36

Чтобы перемножить два отрицательных числа, надо перемножить их модули.
( — 3,2 ) • ( — 9 ) = │ — 3,2 │• │ — 9 │= 3,2 • 9 = 28,8
Или ( — 3,2 ) • ( — 9 ) = 3,2 • 9 = 28,8

Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.
( — 12 ) ÷ ( — 4 ) =│-12│ ÷ │ -4│ = 3
Или ( — 12 ) ÷ ( — 4 ) =12 ÷ 4 = 3

При делении чисел с разными знаками, надо:
 Разделить модуль делимого на модуль делителя;
 Поставить перед полученным числом знак — .
3,6 ÷ ( — 3 ) = — ( 3,6 ÷ 3 ) = — 1,2
( —

Делить на нуль нельзя!

Рациональные числа 6кл.М.10
Число, которое можно записать в виде отношения , где a- целое число, а n – натуральное число, называют рациональным числом.
Любое целое число а является рациональным числом, т.к. его можно записать в виде .
-3 = 0=
Сумма, разность и произведение рациональных чисел тоже рациональное число.
Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.
Свойства действий с рациональными числами
• Переместительное свойство сложения
a + b = b + a
• Сочетательное свойство сложения
a + ( b + c ) = ( a + b ) + c
• Прибавление нуля не изменяет числа
а + 0 = а
• Сумма противоположных чисел равна нулю
а + ( — а ) = 0
• Переместительное свойство умножения
ab = ba
• Сочетательное свойство умножения
a ( b c ) = ( a b ) c
• Распределительное свойство умножения относительно сложения
( a + b ) c = ac + bc
• a • 1=a, a • 1, если а≠0, а • 0 = 0
Раскрытие скобок 6 кл.М.11

Если перед скобками стоит знак + , то можно опустить скобки и этот знак +, сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком + .
a + ( b + c ) = a + b + c a + ( — b + c ) = a – b + c
Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.
— ( a + b ) = — a – b
Чтобы раскрыть скобки, перед которыми стоит знак — , надо заменить этот знак на + , поменяв знаки всех слагаемых в скобках на противоположные. А потом раскрыть скобки.
Коэффициент
Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом ( или просто коэффициентом)
0,3а • ( — 0,7 b) = — 0,21 ab
Подобные слагаемые
Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
— 9х + 7х — 5х + 2х = ( -9 +7 -5 +2)х= — 5х
Решение уравнения
Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак.

Перпендикулярные прямые 6 кл.М.12
Две прямые, образующие при пересечении прямые углы, называются перпендикулярными.
А С
АВ СД
О
В
Д
Отрезки или лучи , лежащие на перпендикулярных прямых, называют перпендикулярными отрезками или лучами.
Параллельные прямые
Две не пересекающиеся прямые на плоскости называют параллельными.
В
А АВ │ СД

С Д

Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны.
c a c, b c a││b
а
b

через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.

Математика
6 класс
1. Делители и кратные . Признаки делимости
2. НОД и НОК
3. Сложение и вычитание дробей с разными знаменателями
4. Умножение и деление обыкновенных дробей
5. Отношения и пропорции
6. Длина окружности. Площадь круга.
7. Положительные и отрицательные числа. Модуль числа

8. Сложение и вычитание положительных и отрицательных чисел
9. Умножение и деление положительных и отрицательных чисел
10. Рациональные числа
11. Раскрытие скобок. Подобные слагаемые
12. Перпендикулярные прямые. Параллельные прямые

Полный текст материала Справочные таблицы по математике 6 класс смотрите в скачиваемом файле.
На странице приведен фрагмент.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Есть мнение?
Оставьте комментарий

Оставить комментарий

Опорная таблица по курсу математики 6 класса — К уроку — Математика, алгебра, геометрия

Опорная таблица
по курсу математики 6 класса.

План-конспект занятия по математике (5, 6 класс) на тему: Зачет по правилам 6 класса (математика)

Знай наизусть!

Правила 5 класса

1. Чтобы найти неизвестный множитель, надо произведение разделить на другой множитель

2. Чтобы найти неизвестное делимое, надо частное умножить на делитель

3. Чтобы найти неизвестный делитель, надо делимое разделить на частное

4. Распределительное свойство умножения относительно сложения: Для того, чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить получившееся произведение    (a + b) c = ac + bc

5. Распределительное свойство умножения относительно вычитания: Для того, чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе

(a — b) c = ac — bc

6. Чтобы сложить (вычесть) десятичные дроби, нужно:

1. Уравнять в этих дробях количество знаков после запятой;
2. Записать их друг под другом так, чтобы запятая была записана под запятой;
3. Выполнить сложение (вычитание), не обращая внимания на запятую;
4. Поставить в ответе запятую под запятой

7. Чтобы умножить десятичную дробь на натуральное число, нужно:

1. Умножить её на это число, не обращая внимания на запятую;
2. В полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби

8. Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., нужно в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы

9. Чтобы разделить десятичную дробь на натуральное число, нужно;

1. Разделить дробь на это число, не обращая внимания на запятую;
2. Поставить в частном  запятую, когда кончится деление целой части

10. Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., нужно перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе

11. Чтобы перемножить две десятичные дроби, нужно:

1. Выполнить умножение, не обращая внимания на запятые;
2. Отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе

12. Чтобы разделить число на десятичную дробь, нужно:

1. В делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
2. После этого выполнить деление на натуральное число

13. Среднее арифметическое = (сумма чисел) : (количество слагаемых)

14.         0,1 = ;          0,125 = ;          0, 25 = ;          0,2 = ;          0,5 = ;          0,75 =

Правила 6 класса

1. Делителем натурального числа a называют натуральное число, на которое a делится без остатка
2. Кратным натурального числа а называют натуральное число которое делится без остатка на а
3. Признак делимости на 10: если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.
4. Признак делимости на 5: если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.
5. Признак делимости на 2: если запись натурального числа оканчивается цифрой 0, 2, 4, 6, 8, то это число делится без остатка на 2.
6. Признак делимости на 9: если сумма цифр числа делится на 9, то это число делится без остатка на 9.
7. Признак делимости на 3: если сумма цифр числа делится на 3, то это число делится без остатка на 3.
8. Натуральное число называют простым, если оно имеет только два делителя: единицу и само это число.
9. Натуральное число называют составным, если оно имеет более двух делителей.
10. Разложить число на простые множители значит представить его в виде произведения простых множителей.
11. Наибольшее натуральное число, на которое делятся без остатка числа а и b, называют наибольшим общим делителем (НОД) этих чисел.
12. Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен единице.
13. Чтобы найти НОД нескольких натуральных чисел, нужно:

1. разложить их на простые множители;
2. составить произведение всех простых множителей, общих для данный чисел.

14. Наименьшим общим кратным (НОК) натуральных чисел а и b называется наименьшее натуральное число, которое кратно и а, и b.
15. Чтобы найти НОК нескольких натуральных чисел, нужно:

1. Разложить их на простые множители;
2. Выписать множители, входящие в разложение одного из чисел;
3. Добавить к ним недостающие множители из разложения остальных чисел;
4. Найти произведение получившихся множителей.

Рабочая программа по математике 6 класс

Пояснительная записка.

Настоящая программа составлена на основе Программы по математике для 5-6 классов Н.Я. Виленкина 2006 года и федерального компонента государственного стандарта основного общего образования (приложение к приказу Минобразования России от 05.03.2004 г. № 1089), рассчитанной для общеобразовательных учреждений.

Выбор данной программы обусловлен тем, что программа реализует стандарт математического образования: уровень требований к математической подготовке, минимальный объём содержания по предмету за курс основной школы. Также имеется методический комплект, который включает в себя учебник: «Математика 6. Учебник для 6 класса общеобразовательных учреждений./ Н.Я.Виленкин, В.И.Жохов и др. – М.: Просвещение, 2007 г.», и дидактические материалы к данному учебнику: «Чесноков А.С., Нешков К.И. Дидактические материалы по математике для 6 класса. – М.: Просвещение, 2008 г.»

Изучение математики на ступени основного общего образования направлено на достижение следующих целей:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.

Курс строится на индуктивной основе с привлечением элементов дедуктивных рассуждений. Теоретический материал курса излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил.

Программа является традиционной, содержание программы совпадает с базисным минимумом, позволяет достичь обязательного минимума умений, которые прописаны в требованиях к математической подготовке учащихся. Тематическое планирование полностью соответствует тематическому планированию по программе данных авторов. Но кроме традиционных уроков в связи с введением инновационных технологий проводятся уроки с использованием компьютера.

Программа рассчитана на 5 часов в неделю (175 часов в год), что соответствует Базисному учебному плану 2004 года и учебному плану школы.

Проверка усвоения знаний, умений и навыков будет осуществляться в ходе фронтального, индивидуального, парного опроса, путём проведения проверочных, самостоятельных, контрольных работ.

Требования к обязательному уровню усвоения полностью совпадают с требованиями основного общего образования по математике.

Требования к уровню подготовки учащихся  в 6 классе

В результате изучения математики ученик должен

знать/понимать

• существо понятия алгоритма; приводить примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математический язык может описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

Арифметика

уметь

• выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;

• переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь – в виде процентов

• выполнять арифметические действия с рациональными числами, сравнивать рациональные числа; находить значения числовых выражений;

• округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;

• пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;

• решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;

• решать линейные уравнения.

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;

• устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов.

Алгебра

уметь

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, выражать из формул одну переменную через остальные;

• решать линейные уравнения;

• изображать числа точками на координатной прямой;

• определять координаты точки плоскости, строить точки с заданными координатами;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;

Геометрия

уметь

• распознавать изученные геометрические фигуры, различать их взаимное расположение;

• изображать изученные геометрические фигуры;

• распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

Элементы логики, комбинаторики, статистики и теории вероятностей

уметь

• извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы;

• решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;

• вычислять средние значения результатов измерений;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• распознавания логически некорректных рассуждений;

• анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;

• решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;

• решения учебных и практических задач, требующих систематического перебора вариантов.

СОДЕРЖАНИЕ ПРОГРАММЫ (6 КЛАСС)

1. Делимость чисел (20 ч)

Делимость натуральных чисел. Делители и кратные числа. Наибольший общий делитель и наименьшее общее кратное. Признаки делимости на 2, 3, 5, 9, 10. Простые и составные числа. Разложение натурального числа на простые множители. Контрольная работа №1

Основная цель — завершить изучение натуральных чисел, подготовить основу для освоения действий с обыкновенными дробями.

В данной теме завершается изучение вопросов, связанных с натуральными числами. Основное внимание должно быть уделено знакомству с понятиями «делитель» и «кратное», которые находят применение при сокращении обыкновенных дробей и при их приведении к общему знаменателю. Упражнения полезно выполнять с опорой на таблицу умножения — прямым подбором.

Определенное внимание уделяется знакомству с признаками делимости, понятиям простого и составного чисел. При их изучении целесообразно формировать умения проводить простейшие умозаключения, обосновывая свои действия ссылками на определение, правило.

Учащиеся должны уметь разложить число на множители. Например, они должны понимать, что 36 = 6· 6 = 4· 9 = 2 ·18 и т. п. Умения разложить число на простые множители не обязательно добиваться от всех учащихся.

2. Сложение и вычитание дробей с разными знаменателями (22 ч)

Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Понятие о наименьшем общем знаменателе нескольких дробей. Сравнение дробей. Сложение и вычитание дробей. Решение текстовых задач арифметическим способом. Контрольная работа №2, №3

Основная цель — выработать прочные навыки преобразования дробей, сложения и вычитания дробей.

Одним из важнейших результатов обучения является усвоение основного свойства дроби, применяемого для преобразования дробей: сокращения, приведения к новому знаменателю. Умение приводить дроби к общему знаменателю используется для сравнения дробей.

При рассмотрении действий с дробями используются правила сложения и вычитания дробей с одинаковыми знаменателями, понятие смешанного числа. Важно обратить внимание на случай вычитания дроби из целого числа.

3. Умножение и деление обыкновенных дробей (32 ч)

Умножение и деление обыкновенных дробей. Основные задачи на дроби. Нахождение части от целого и целого по его части. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной дроби в виде десятичной. Контрольная работа №4, №5, №6

Основная цель — выработать прочные навыки арифметических действий с обыкновенными дробями и решения основных задач на дроби.

В этой теме завершается работа над формированием навыков арифметических действий с обыкновенными дробями. Навыки должны быть достаточно прочными, чтобы учащиеся не испытывали затруднений в вычислениях с рациональными числами, чтобы алгоритмы действий с обыкновенными дробями могли стать в дальнейшем опорой для формирования умений выполнять действия с алгебраическими дробями.

Расширение аппарата действий с дробями позволяет решать текстовые задачи, в которых требуется найти дробь от числа или число по данному значению его дроби.

4. Отношения и пропорции (19 ч)

Отношение, выражение отношения в процентах. Пропорция. Основное свойство пропорции. Решение задач с помощью пропорции. Пропорциональная и обратно пропорциональная зависимости величин. Задачи на пропорции. Масштаб. Формулы длины окружности и площади круга. Шар. Контрольная работа №7, №8

Основная цель — сформировать понятия пропорции, прямой и обратной пропорциональности величин.

Необходимо, чтобы учащиеся усвоили основное свойство пропорции, так как оно находит применение на уроках математики, химии, физики. В частности, достаточное внимание должно быть уделено решению с помощью пропорции задач на проценты.

Понятия о прямой и обратной пропорциональности величин можно сформировать как обобщение нескольких конкретных примеров, подчеркнув при этом практическую значимость этих понятий, возможность их применения для упрощения решения соответствующих задач.

В данной теме даются представления о длине окружности и площади круга. Соответствующие формулы к обязательному материалу не относятся. Рассмотрение геометрических фигур завершается знакомством с шаром.

5. Положительные и отрицательные числа (13 ч)

Целые числа: положительные, отрицательные числа и нуль. Противоположные числа. Модуль (абсолютная величина) числа и его геометрический смысл. Сравнение чисел. Изображение чисел на координатной прямой. Координата точки. Формула расстояния между двумя точками плоскости. Контрольная работа №9

Основная цель — расширить представления учащихся о числе путем введения отрицательных чисел.

Целесообразность введения отрицательных чисел показывается на содержательных примерах. Учащиеся должны научиться изображать положительные и отрицательные числа на координатной прямой. В дальнейшем она будет служить наглядной основой для правил сравнения чисел, сложения и вычитания чисел.

Специальное внимание должно быть уделено усвоению вводимого здесь понятия модуля числа, прочное знание которого необходимо для формирования умения сравнивать отрицательные числа, а в дальнейшем и для овладения алгоритмами арифметических действий с положительными и отрицательными числами.

6. Сложение и вычитание положительных и отрицательных чисел (11 ч)

Сложение и вычитание положительных и отрицательных чисел. Контрольная работа №10

Основная цель — выработать прочные навыки сложения и вычитания положительных и отрицательных чисел.

Действия с отрицательными числами вводятся на основе представлений об изменении величин: сложение и вычитание чисел иллюстрируется соответствующими перемещениями точек координатной прямой. При изучении данной темы отрабатываются алгоритмы сложения и вычитания при выполнении действий с целыми и дробными числами.

7. Умножение и деление положительных и отрицательных чисел (12 ч)

Умножение и деление положительных и отрицательных чисел. Понятие о рациональном числе. Сравнение рациональных чисел, арифметические действия с рациональными числами. десятичное приближение обыкновенной дроби. Законы арифметических действий: переместительный, сочетательный, распределительный. Контрольная работа №11

Основная цель — выработать прочные навыки арифметических действий с положительными и отрицательными числами.

Навыки умножения и деления положительных и отрицательных чисел отрабатываются сначала при выполнении отдельных действий, а затем в сочетании с навыками сложения и вычитания при вычислении значений числовых выражений.

При изучении данной темы учащиеся должны усвоить, что для обращения обыкновенной дроби в десятичную достаточно разделить (если это возможно) числитель на знаменатель. В каждом конкретном случае они должны знать, в какую дробь обращается данная обыкновенная дробь — в десятичную или периодическую. Учащиеся должны знать представление в виде десятичной дроби таких дробей, как

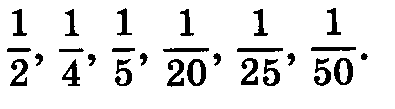
8. Решение уравнений (15 ч)

Простейшие преобразования выражений: раскрытие скобок, приведение подобных слагаемых. Решение линейных уравнений. Примеры решения текстовых задач с помощью линейных уравнений. Контрольная работа №12, №13

Основная цель — подготовить учащихся к выполнению преобразований выражений, решению уравнений.

Преобразования буквенных выражений путем раскрытия скобок и приведения подобных слагаемых отрабатываются в той степени, в которой они необходимы для решения несложных уравнений.

Введение арифметических действий над отрицательными числами позволяет ознакомить учащихся с общими приемами решения линейных уравнений с одной переменной.

9. Координаты на плоскости (13 ч)

Построение перпендикуляра к прямой и параллельных прямых с помощью чертежного треугольника и линейки. Изображение чисел точками координатной прямой. Прямоугольная система координат на плоскости, координаты точки, абсцисса и ордината точки. Примеры графиков, диаграмм. Контрольная работа №14

Основная цель — познакомить учащихся с прямоугольной системой координат на плоскости.

Учащиеся должны научиться распознавать и изображать перпендикулярные и параллельные прямые. Основное внимание следует уделить отработке навыков их построения с помощью линейки и чертежного треугольника, не требуя воспроизведения точных определений.

Основным результатом знакомства учащихся с координатной плоскостью должны стать знания порядка записи координат точек плоскости и их названий, умения построить координатные оси, отметить точку по заданным координатам, определить координаты точки, отмеченной на координатной плоскости.

Формированию вычислительных и графических умений способствует построение столбчатых диаграмм. При выполнении соответствующих упражнений найдут применение изученные ранее сведения о масштабе и округлении чисел.

10. Повторение. Решение задач. (18 ч)

Делимость чисел. Сложение и вычитание дробей с разными знаменателями. Умножение и деление обыкновенных дробей. Решение уравнений. Отношения и пропорции. Положительные и отрицательные числа. Сложение и вычитание положительных и отрицательных чисел. Умножение и деление положительных и отрицательных чисел. Итоговая контрольная работа. Анализ результатов контрольной работы

Учебно-тематическИЙ план по математике в 6 классе

№

п/п

Раздел

Кол-во часов (всего)

В том числе

Контрольная работа

1

Делимость чисел

20

1

2

Сложение и вычитание дробей с разными знаменателями

22

2

3

Умножение и деление обыкновенных дробей

32

3

4

Отношения и пропорции

19

2

5

Положительные и отрицательные числа

13

1

6

Сложение и вычитание положительных и отрицательных чисел

11

1

7

Умножение и деление положительных и отрицательных чисел

12

1

8

Решение уравнений

15

2

9

Координаты на плоскости

13

1

10

Повторение

18

1

Итого

175

15

ПОУРОЧНОЕ ПЛАНИРОВАНИЕ ПО МАТЕМАТИКЕ В 6 КЛАССЕ

Тема раздела

№ урока

Тема урока

Делимость чисел

20 часов

1-3

Делители и кратные

4-6

Признаки делимости на 10, на 5, на 2

7-8

Признаки делимости на 9 и на 3

9-10

Простые и составные числа

11-12

Разложение на простые множители

13-15

Наибольший общий делитель.

Взаимно простые числа

16-19

Наименьшее общее кратное

20

Контрольная работа № 1 по теме

«Делимость чисел»

Сложение и вычитание дробей с разными знаменателями

22 часа

21-22

Основное свойство дроби

23-25

Сокращение дробей

26-28

Приведение дробей к общему знаменателю

29-34

Сравнение, сложение и вычитание дробей с разными знаменателями

35

Контрольная работа № 2 по теме «Основное свойство дроби»

36-41

Сложение и вычитание смешанных чисел

42

Контрольная работа № 3по теме «Сложение и вычитание смешанных чисел»

Умножение и деление обыкновенных дробей

32 часа

43-47

Умножение дробей

48-51

Нахождение дроби от числа

52-56

Применение распределительного свойства умножения

57

Контрольная работа № 4 по теме «Умножение дробей»

58-59

Взаимно обратные числа

60-64

Деление

65

Контрольная работа № 5 по теме «Деление дробей»

66-70

Нахождение числа по его дроби

71-73

Дробные выражения

74

Контрольная работа № 6 по теме «Дробные выражения»

Отношения и пропорции

19 часов

75-77

Отношения

78-82

Пропорции

83-85

Прямая и обратная пропорциональная зависимость

86

Контрольная работа №7 по теме «Отношения и пропорции»

87-89

Масштаб

90-91

Длина окружности и площадь круга

92-93

Шар

94

Контрольная работа №8 по теме «Масштаб»

Положительные и отрицательные числа

13 часов

95-97

Координаты на прямой

98-99

Противоположные числа

100-101

Модуль числа

102-104

Сравнение чисел

105-106

Изменение величин

107

Контрольная работа №9 по теме «Положительные и отрицательные числа»

Сложение и вычитание положительных и отрицательных чисел

11 часов

108-109

Сложение чисел с помощью координатной прямой

110-111

Сложение отрицательных чисел

112-114

Сложение чисел с разными знаками

115-117

Вычитание

118

Контрольная работа №10 по теме «Сложение и вычитание положительных и отрицательных чисел»

119-121

Умножение

122-124

Деление

Умножение и деление положительных и отрицательных чисел

12 часов

125-126

Рациональные числа

127-129

Свойства действий с рациональными числами

130

Контрольная работа №11по теме «Умножение и деление положительных и отрицательных чисел»

Решение уравнений

15 часов

131-134

Раскрытие скобок

135-136

Коэффициент

137-139

Подобные слагаемые

140

Контрольная работа №12 по теме «Раскрытие скобок»

141-144

Решение уравнений

145

Контрольная работа №13 по теме «Решение уравнений»

Координаты на плоскости

13 часов

146-147

Перпендикулярные прямые

148-149

Параллельные прямые

150-151

Координатная плоскость

152-153

Столбчатые диаграммы

154-156

Графики

157

Контрольная работа №14 по теме «Координаты на плоскости»

Повторение

18 часов

158-159

Делимость чисел

160-161

Сложение и вычитание дробей с разными знаменателями

162-163

Умножение и деление обыкновенных дробей

164-165

Решение уравнений

166-167

Отношения и пропорции

168-169

Положительные и отрицательные числа

170-171

Сложение и вычитание положительных и отрицательных чисел

172-173

Умножение и деление положительных и отрицательных чисел

174

Контрольная работа №15 по курсу математики 6 класса

175

Анализ результатов контрольной работы

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ

• Математика. 6 класс: учебник для общеобразовательных учреждений/ Виленкин Н.Я. и др. — М.: Мнемозина, 2011

• Дидактические материалы по математике: 6 класс: практикум/ Чесноков А.С., Нешков К.И. – 4 изд. – М.: Академкнига/Учебник, 2012.

• Жохов В.И. Математические диктанты. 5-6 класс: Пособие для учителей и учащихся.

• В.И.Жохов. Разработки уроков, нормативные и контрольно-методические материалы: Математика. 5-6. Книга для учителя. – М.:ИЛЕКСА, 2007.

• Математика. 5 класс: Поурочные планы по учебнику Н.Я.Виленкина, В.И.Жохова. I, II полугодие/ авт.-сост. Л.А. Тапилина, Т.Л.Афанасьева. – Волгоград: Учитель, 2005.

• Математика. 6 класс: Поурочные планы по учебнику Н.Я.Виленкина, В.И.Жохова. I, II полугодие/ авт.-сост. Л.А. Тапилина, Т.Л.Афанасьева. – Волгоград: Учитель, 2005.