Урок по математике в 6 классе «Решение уравнений»
В данной работе приведен пример использования методов и приемов НФТМ-ТРИЗ при обучении математике в 6 классе.
Разработка урока
Предмет: математика
Класс: 6
Тема: «Решение уравнений»
Тип урока: урок обобщения и систематизации знаний по теме «Решение уравнений».
Цель урока: закрепление основных приёмов преобразования линейных уравнений и методов их решения.
Задачи:
Образовательная:
1. Проверить и обобщить знания и умения учащихся по теме «Решение уравнений».
2. Проверить умение выполнять арифметические действия с целыми и дробными числами.
Развивающая:
1. Развивать логическое мышление.
2. Активизировать мыслительную деятельность, познавательную активность.
3.Формировать навыки самоконтроля, адекватной самооценки и саморегуляции собственной деятельности.
Воспитательная:
1. Воспитывать аккуратность, трудолюбие.
2. Развивать общую культуру личности.
3. Способствовать толерантному воспитанию учащихся.
Формы организации учебной деятельности: индивидуальная, фронтальная, парная.
Средства: компьютер, интерактивная доска, набор индивидуальных карточек, презентация к уроку, наглядные пособия,
План урока.
Организационный момент.
II. Постановка темы и цели урока. Мотивация к учебной деятельности.
III. Актуализация знаний.
IV. Обобщение и систематизация знаний. Воспроизведение на новом уровне (переформулированные вопросы).
Физкультминутка.
V. Применение знаний и умений в новой ситуации.
VI. Контроль усвоения знаний и умений.
VII. Рефлексия.
VIII. Подведение итогов урока. Постановка домашнего задания.
Ход урока.
Организационный момент.
Цель этапа: Приветствие учащихся. Проверка готовности к уроку. Психологический настрой на урок.
II. Постановка темы и цели урока. Мотивация к учебной деятельности.
Цель этапа: Мотивация к учебной деятельности.
(Прием «Отстроченная отгадка». Универсальный приём ТРИЗ, направленный на активизацию мыслительной деятельности учащихся на уроке).
Задание 1. Записать слова (работа по цепочке у доски):
Задание 2. Дать толкование этих понятий. Ребята, как Вы думаете, к какой теме относятся эти понятия?
Задание 3. Старинная задача (Прием «Творческого разогрева», применение которого предполагает различные творческие задания в форме игры. Игра – форма деятельности учащихся, в которой осознается окружающий мир, открывается простор для личной активности и творчества).
В клетке сидят фазаны и кролики. У них 19 голов и 62 ноги. Сколько фазанов и сколько кроликов в клетке?
Актуализация знаний. (Прием «Интеллектуальная разминка», начинается с одного или нескольких небольших заданий, загадок, которые ученики могут решить, опираясь на ранее изученный материал. На экране появляются по очереди задания. Правильные ответы появляются по щелчку после ответов учащихся).
Цель этапа: актуализация знаний, совершенствовать вычислительные навыки, сформулировать правила решения уравнений.
Задание 1. Решить уравнения:
а) 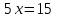 б)
б) 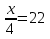 в)
в) 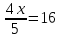
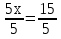
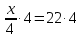
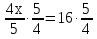
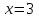
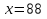
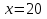
Задание 2. Сформулируйте правило, которое Вы применили при решении данных уравнений (Корни уравнения не изменятся, если его обе части разделить или умножить на одно и то же число, не равное 0).
Задание 3. Решить уравнения:
а) 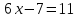 б)
б) 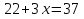
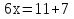
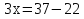
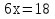
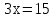
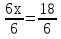
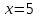
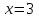
Задание 4. Сформулируйте правило, которое Вы применили при решении данных уравнений (Корни уравнения не изменятся, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак).
Задание 5. Решить уравнение: 5x+13=3x-3
Задание 6. Сформулируйте правило, которое Вы применили при решении данного уравнения (Если в уравнении присутствуют подобные слагаемые, следует):
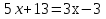
Перенести все подобные в одну часть уравнения, а числовые слагаемые в другую:

Привести подобные слагаемые:

Решить уравнение:

IV. Обобщение и систематизация знаний. Воспроизведение на новом уровне (переформулированные вопросы).
Цель этапа: проверка уровня сформированности навыка в новой ситуации.
Задание: Ответить на вопросы:
Что называется уравнением?
Что значит решить уравнение?
Что называется корнем уравнения?
Задание 7. Составить алгоритм решения уравнения (на основе самоанализа устных упражнений учащиеся составляют алгоритм решения уравнений).
(Прием «Психологическая разгрузка» — это эффект расслабления нервной системы при больших нагрузках и усталости).
Историческая справка (опережающее домашнее задание). Девиз опережающего обучения: через знающего ученика обогатить знаниями другого (незнающего).
Многие уравнения умел решать греческий математик Диофант, который даже применял букву для обозначения неизвестных. Но по-настоящему метод уравнения сформировался в руках арабский ученых. Они, по-видимому, знали, как решали задачи в Вавилоне и Индии, улучшили эти способы решения и привели их в систему.
Первым написал книгу на арабском языке о решение уравнений уже знакомый нам Мухаммед ибн Муса ал-Хорезми. Название у нее было очень странное — «Краткая книга об исчисление ал-джабры и ал-мукабал». В этом названии впервые прозвучало известное нам слово «алгебра».
АЛ-ДЖАБРА
это перенос слагаемых из одной части уравнения в другую с противоположным знаком.
При решение уравненья
Если в части одной,
Безразлично какой,
Встретится член отрицательный,
Мы к обеим частям,
С этим членом сличив,
Равный член предадим,
Только с знаком другим,
И найдем результат нам желательный.
АЛ- МУКАБАЛА
— это приведение подобных слагаемых.
Дальше смотрим в уравненье,
Можно ль сделать приведенье,
Если члены в нем подобны
Сопоставить их удобно,
Вычтя равный член из них,
К одному приводим их.
V. Применение знаний и умений в новой ситуации.
Цель этапа: проверка уровня сформированности навыка применения новых знаний и умений в новой ситуации.
Задание 8. Решить уравнение (Прием «Мозговой штурм» — методика активизации группового поиска идей, решения проблемы. Обстановка в процессе ее применения должна быть непринужденной, ученики раскованными, никакой критики и самокритики. Мнение каждого считается ценным и обсуждается. Можно высказывать любые предположения, в том числе парадоксальные и нереальные). Применён метод поиска решений с целью выявления пробелов в знаниях учащихся.
Решить уравнение «Найди ошибку». (Применён метод поиска решений с целью выявления проблемы в знаниях учащихся)
Верное решение
Решение: 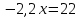
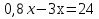
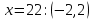
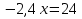
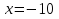
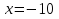
 Верное решение:
Верное решение:
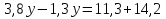
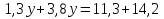
Ошибка 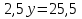
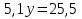
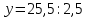
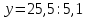
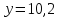
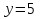
Верное решение:
Ошибка 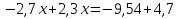 ошибка
ошибка 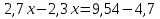
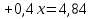
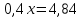
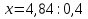
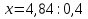
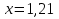 ошибка
ошибка 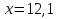
После выполнения данного задания учащиеся исправляют у доски ошибки и приходят к единому ответу.
Задание 9. Решить уравнение (задания разноуровневые по группам выбор задания — по уровню сложности, который указан разным цветом).
(Прием «Преодоление барьера психологической инерции»)
1 группа.
2 2) -2 3) -5
-2 2) 4 3)

0,8 2) -0,8 3) 8
2 группа
-1,76 2) 52,28 3) -52,28
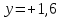
-1,6 2) 1,6 3) 16
0,3 2) -0,1 3) 0,1
3 группа
1 2) -1 3) 2,7
-1 2) -2 3) 2
50 2) -50 3) -5
После того, как выяснен код ответа, обнаруженная ошибка подробно рассматривается на доске.
VI. Контроль усвоения знаний и умений.
Цель этапа: выявление качества и уровня усвоения знаний.
Задание 10. Решить уравнение.
(Прием «Усложняющихся заданий» — это специальная программа рабочих действий, выстроенная по степени их важности, расширения объема задания и повышения сложности. Заключительная ступень — самостоятельное выполнение задания).
Этот этап урока организован так: учащимся даны задания по вариантам. Выполнив своё задание, ученик приступает к решению задания другого варианта (работа в группах).
Решить уравнение:

Решение:
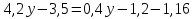
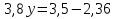
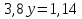
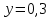
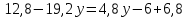
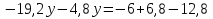
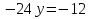
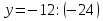
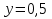
Физкультурная минутка
Задание 11. Решить задачу.
На этом этапе урока осуществляется контроль знаний учащихся.
Задача.
Два велосипедиста отправились одновременно навстречу друг другу из двух пунктов, расстояние между которыми 60 км., и встретились через 2 часа. Определите скорость каждого велосипедиста, если у одного она на 2км/ч больше, чем у другого.
 (км/ч)
(км/ч)t (час)
S (км)
1-ый велосипедист
2
2-ой велосипедист
2
Два пешехода вышли одновременно навстречу друг другу из двух посёлков и встретились через 3 часа. Расстояние между посёлками 30 км. Найдите скорость каждого пешехода, если у одного она 2км/ч меньше, чем у другого.
 (км/ч)
(км/ч)t (час)
S (км)
1-ый пешеход
3
2-ой пешеход
3
Теплоход «Ракета» прошёл расстояние между пристанями со скоростью 50км/ч за 4,8 ч. С какой скоростью должен идти теплоход, чтобы пройти это расстояние за 3,2 часа?
Ответы к заданиям записаны на доске и сообщены учащимся после сдачи работы. Тем самым учащиеся были озадачены нахождением верного решения.
VII. Рефлексия. (Прием «Обратная связь» означает отзыв, отклик, ответную реакцию на какое-либо действие или событие. Например, водитель во время движения постоянно поддерживает обратную связь, считывая информацию с приборов, дорожных знаков, получая ее от своих органов чувств. На основе этих данных он корректирует свои действия и маршрут. Постоянная обратная связь, которую получают учащиеся, подобно водителю, дает им возможность оценивать свои успехи и согласовывать свои действия с первоначальными критериями. Мнение учителя, с которым ученик взаимодействует на уроке, обратная связь от учителя — это отличный материал, который можно использовать в качестве основы развития своей личной и профессиональной эффективности)
Цель этапа: подведение итогов выполнения тестовой работы. Самооценка собственной деятельности.
Ребята, что нового узнали на уроке (составлен алгоритм решения уравнения).
Тест по теме «Решение уравнений» (самопроверка с кодом ответа). (Прием « Да-нет». Универсальный приём технологии ТРИЗ: способен увлечь и маленьких, и взрослых; ставит учащихся в активную позицию).
Вариант 1
Вариант 2
Является ли число 2 корнем уравнения -2х+4=0
да 2) нет
Является ли число -2 корнем уравнения 2х+4=0
да 2) нет
Реши уравнение
-1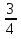 +х =0
+х =0
1) 1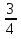 ; 2) -1
; 2) -1 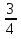 ; 3) 0
; 3) 0
2. Реши уравнение
6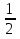 — х = 6
— х = 6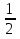
1) 6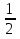 ; 2) -6
; 2) -6 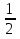 ; 3) 0
; 3) 0
Реши уравнение
-0, 75 + 3х = -0,75
1) -0,5 2) 0,5 3) 0
Код ответа: 113
3. Реши уравнение
— 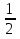 х + 7,3 = 8,3
х + 7,3 = 8,3
1) 7,8 2) -2 3) — 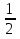
Код ответа: 132
Резюме
VIII. Подведение итогов урока. Постановка домашнего задания.
Цель этапа: проведение инструктажа по выполнению домашнего задания.
Домашнее задание (разноуровневое) — по карточкам.
№1. Решите уравнение:
А) 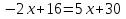
Б) 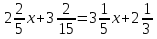
№2. Решите уравнение:
А) 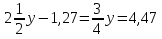
Б) Первое число в 1,4 раза больше второго. Если от первого числа отнять 5,2, а ко второму прибавить 4,8, то получатся равные результаты.
№3.
А) Решить уравнение: 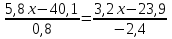
Б) В первом вагоне в 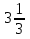 раза груза больше, чем во втором. Если из первого вагона снять
раза груза больше, чем во втором. Если из первого вагона снять 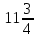 m, а во второй добавить
m, а во второй добавить 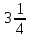 m, то груза в вагонах станет поровну. Сколько тонн груза было в каждом вагоне?
m, то груза в вагонах станет поровну. Сколько тонн груза было в каждом вагоне?
Алгоритм решения линейного уравнения
Раскрыть скобки, если они присутствуют в уравнении.
Перенести слагаемые с переменной в одну часть уравнения, а без переменной в другую часть.
Привести подобные слагаемые.
Умножить (разделить) обе части уравнения на одно и тоже число.
Найти корни уравнения.
Применяемые методы и приемы в преподавании математики преследуют цели, предъявляемые современному школьному образованию, основной задачей которого является развитие творческого потенциала школьника, формирование креативной творческой личности, что является основной задачей ФГОС. Решению этой задачи способствует применение технологии НФТМ-ТРИЗ на уроках.
Ссылки на источники
1.Федеральный государственный образовательный стандарт основного общего образования: Федеральный закон Российской Федерации от 17 декабря 2010 г. № 1897-ФЗ.
2.Виленкин Н.Я. Математика 6 класс: учебник. Для общеобразовательных учреждений / М.:Мнемозина,2008. 289с.
3.Утемов В.В. Задачи открытого типа как средство развития креативности учащихся средней школы //Концепт: научно- методический электронный журнал официального сайта эвристических олимпиад «Совёнок» и «Прорыв» -Декабрь 2011,АКТ1102-Киров, 2011-URLhttp//www.covenok.ru /concept/2011/1102.htm
4.Утёмов В.В. Технология формирования креативного мышления на основе задач открытого типа //Вестник Сургутского государственного педагогического университета.-2011.-№3.- С51-57
5.Утёмов В.В., Зиновкина М.М. Структура креативного урока по развитию творческой личности учащихся в педагогической системе НФТМ-ТРИЗ //Концепт.- 2013.-Современные научные исследования. Выпуск 1.-ART 53572.-URL: http:ru/e-koncept.ru/2013/53572/htm
6. Утёмов В.В. ТРИЗ-педагогика: использование ТРИЗ в обучении школьников математике.-Saarbrucken: AV Akademikerveland, 2012.-90с.
Уравнения по математике для 6 класса
Автор Administrator На чтение 2 мин. Опубликовано
В 6 классе осуществляется основная работа по подготовке учащихся к изучению более сложного предмета – алгебры. Учителя закладывают фундамент для решения задач по алгебре в будущем. Уравнения, которые ученики решают в 6 классе помогут им впоследствии понять важные алгебраические процессы. Сборник, включающий в себя все виды математических уравнений за 6 класс, отлично в этом поможет.
В 6 классе осуществляется основная работа по подготовке учащихся к изучению более сложного предмета – алгебры. Учителя закладывают фундамент для решения задач по алгебре в будущем. Уравнения, которые ученики решают в 6 классе помогут им впоследствии понять важные алгебраические процессы. Сборник, включающий в себя все виды математических уравнений за 6 класс, отлично в этом поможет.
“Уравнения по математике для 6 класса” – отлично составленное методическое пособие, которое содержит в себе всю информацию по теме уравнения за 6 класс. Оно включает в себя:
- теоретическую часть, которая в полном объеме раскрывает учебный материал;
- примеры уравнений разных видов и способы их решений;
- практическую часть, которая дает возможность проверить полученные знания.
Систематическое решение математических уравнений в 6 классе поможет учащимся довести свои действия до автоматизма, даст понять, что в будущем при решении других задач и уравнений они могут воспользоваться уже полученными навыками.
Издательство: Все Для Детей
Год издания: 2014
Автор: Все Для Детей
Формат: PDF
Количество страниц: 17
Язык: Русский
Скачать бесплатно uravneniya-po-mamematike-6-klass.pdf
Урок математики в 6 классе «Решение уравнений»
Тема Решение уравнений 6а класс (1-ый урок)
Цель: 1. Отработать навыки решения уравнений.
2. Проверить знания по теме «Раскрытие скобок и приведение подобных слагаемых»
3. Совершенствовать умения применять знания к решению уравнений.
4. Развивать правильную речь.
Ход урока.
Учитель: Эпиграф нашего урока
«Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать уравнения, то решайте их» Д.Пойа
(записан на доске)
Если человек своим трудолюбием, упорством ежедневно достигает истины в чем-либо, то маленькие ежедневные удачи построят большой успех в будущем. На сегодняшнем уроке мы тоже попытаемся достичь маленького успеха для нашего будущего. Для этого надо быть настойчивым и внимательным.
— Чем же мы будем заниматься на уроке? (Решать уравнения)
— А как вы думаете, какие преобразования алгебраических выражений будем выполнять при решении уравнений?
(Раскрытие скобок, приведение подобных слагаемых, перенесение слагаемых из одной части в другую, вычислительные навыки).
На уроке нужно успеть очень многое, будьте предельно собраны и внимательны.
I. Проверка домашнего задания по проектору. №106(д, е, ж)
д + 5 = +3
е) 1,2d – 0,5(4d – 1) = -0,7(d – 2)
ж) — (у + ) = — ( + 0,5)
II. Блицтурнир. Устная работа. Слайд 2 (Презентация «Решение уравнений 1)
а) повторить правила сложения, вычитания, умножения, деления рациональных чисел
II. Устно:
а) повторение компонентов: 1) 2х = 4,2
2) х : 2,3 = 2,7
3) 35 : х = 0,7
4) -8,4 = 3х По слайдам
б) раскрытие скобок и приведение подобных слагаемых
1) (x – y + z)5 2) -3х ? (-2у) 3) 10a + d — 10d — a
4) -5(x — 3)+4(x — 2) 5) – (у + 1,2) – 2,5(2 – у)
Работа в парах, проверить друг у друга
III. Переходим к решению уравнений:
— Что называется уравнением?
— Что значит решить уравнение?
— Что такое корень уравнения?
— Какие преобразования необходимо делать при решении уравнений?
Задание: найди ошибку в высказывании. Слайды
Решить уравнение: — 0,2(-3у – 0,4) – ( — 0,5 + у) = 1
0,6у + 0,08 + 0,5 – у = 1
0,6у – у = 1 – 0,08 – 0,5
— 0,4у = 0,42
у = — 1,05 Ответ: — 1,05
У доски решает Зотова Анна
IV. Самостоятельная работа: 2 варианта ( на листочках, раздать заранее)
Вариант 1
- Упростите: — 0,2а ? 5d
- Раскройте скобки и приведите подобные слагаемые:
а) – 2(-0,4х + 2) – (3х – 8)
б) – 3( — 0,8у + ) + 4 ( — — 2у)
- Решить уравнение:
а) 7m+1=8m+9
б) -3(2х+1)=3(-11+х)
Дополнительно: =
Вариант 2
- Упростите: 0,6 х ? ( — 2у)
- Раскройте скобки и приведите подобные слагаемые:
а) 0,3 (- 2а + 3) – ( 9 + а)
б) — 2(0,1х -) – 3(+ 6х)
- Решить уравнение:
а) -12m + 3=11m – 3
б) 4(х — 3)-16 = 5(х — 5)
Дополнительно: =
V. Домашнее задание. № 100 (д, е), №111 (д, е)
Самостоятельная работа: __________________________
Вариант 1
- Упростите: — 0,2а ? 5d =
- Раскройте скобки и приведите подобные слагаемые:
а) – 2(-0,4х + 2) – (3х – 8) =
б) – 3( — 0,8у + ) + 4 ( — — 2у) =
- Решить уравнение:
а) 7m+1=8m+9
б) -3(2х + 1) = 3(- 11 + х)
Дополнительно: =
Самостоятельная работа: __________________________
Вариант 2
- Упростите: 0,6 х ? ( — 2у) =
- Раскройте скобки и приведите подобные слагаемые:
а) 0,3 (- 2а + 3) – ( 9 + а) =
б) — 2(0,1х -) – 3(+ 6х) =
- Решить уравнение:
а) -12m + 3=11m — 3
б) 4(х — 3) – 16 = 5(х — 5)
Дополнительно: =
Просмотр содержимого документа
«Конспект урока»
Тема Решение уравнений 6а класс (1-ый урок)
Цель: 1. Отработать навыки решения уравнений.
2. Проверить знания по теме «Раскрытие скобок и приведение подобных слагаемых»
3. Совершенствовать умения применять знания к решению уравнений.
4. Развивать правильную речь.
Ход урока.
Учитель: Эпиграф нашего урока
«Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать уравнения, то решайте их» Д.Пойа
(записан на доске)
Если человек своим трудолюбием, упорством ежедневно достигает истины в чем-либо, то маленькие ежедневные удачи построят большой успех в будущем. На сегодняшнем уроке мы тоже попытаемся достичь маленького успеха для нашего будущего. Для этого надо быть настойчивым и внимательным.
— Чем же мы будем заниматься на уроке? (Решать уравнения)
— А как вы думаете, какие преобразования алгебраических выражений будем выполнять при решении уравнений?
(Раскрытие скобок, приведение подобных слагаемых, перенесение слагаемых из одной части в другую, вычислительные навыки).
На уроке нужно успеть очень многое, будьте предельно собраны и внимательны.
I. Проверка домашнего задания по проектору. №106(д, е, ж)
д  + 5 =
+ 5 =  +3
+3
е) 1,2d – 0,5(4d – 1) = -0,7(d – 2)
ж)  — (у +
— (у +  ) =
) =  — (
— ( + 0,5)
+ 0,5)
II. Блицтурнир. Устная работа. Слайд 2 (Презентация «Решение уравнений 1)
а) повторить правила сложения, вычитания, умножения, деления рациональных чисел
II. Устно:
а) повторение компонентов: 1) 2х = 4,2
2) х : 2,3 = 2,7
3) 35 : х = 0,7
4) -8,4 = 3х По слайдам
б) раскрытие скобок и приведение подобных слагаемых
1) (x – y + z)5 2) -3х ∙ (-2у) 3) 10a + d — 10d — a
4) -5(x — 3)+4(x — 2) 5) – (у + 1,2) – 2,5(2 – у)
Работа в парах, проверить друг у друга
III. Переходим к решению уравнений:
— Что называется уравнением?
— Что значит решить уравнение?
— Что такое корень уравнения?
— Какие преобразования необходимо делать при решении уравнений?
Задание: найди ошибку в высказывании. Слайды
Решить уравнение: — 0,2(-3у – 0,4) – ( — 0,5 + у) = 1
0,6у + 0,08 + 0,5 – у = 1
0,6у – у = 1 – 0,08 – 0,5
— 0,4у = 0,42
у = — 1,05 Ответ: — 1,05
У доски решает Зотова Анна
IV. Самостоятельная работа: 2 варианта ( на листочках, раздать заранее)
Вариант 1
Упростите: — 0,2а ∙ 5d
Раскройте скобки и приведите подобные слагаемые:
а) – 2(-0,4х + 2) – (3х – 8)
б) – 3( — 0,8у +  ) + 4 ( —
) + 4 ( —  — 2у)
— 2у)
Решить уравнение:
а) 7m+1=8m+9
б) -3(2х+1)=3(-11+х)
Дополнительно:  =
= 
Вариант 2
Упростите: 0,6 х ∙ ( — 2у)
Раскройте скобки и приведите подобные слагаемые:
а) 0,3 (- 2а + 3) – ( 9 + а)
б) — 2(0,1х — ) – 3(
) – 3( + 6х)
+ 6х)
Решить уравнение:
а) -12m + 3=11m – 3
б) 4(х — 3)-16 = 5(х — 5)
Дополнительно: 
 =
= 
V. Домашнее задание. № 100 (д, е), №111 (д, е)
Самостоятельная работа: __________________________
Вариант 1
Упростите: — 0,2а ∙ 5d =
Раскройте скобки и приведите подобные слагаемые:
а) – 2(-0,4х + 2) – (3х – 8) =
б) – 3( — 0,8у +  ) + 4 ( —
) + 4 ( —  — 2у) =
— 2у) =
Решить уравнение:
а) 7m+1=8m+9
б) -3(2х + 1) = 3(- 11 + х)
Дополнительно:  =
= 
Самостоятельная работа: __________________________
Вариант 2
Упростите: 0,6 х ∙ ( — 2у) =
Раскройте скобки и приведите подобные слагаемые:
а) 0,3 (- 2а + 3) – ( 9 + а) =
б) — 2(0,1х — ) – 3(
) – 3( + 6х) =
+ 6х) =
Решить уравнение:
а) -12m + 3=11m — 3
б) 4(х — 3) – 16 = 5(х — 5)
Дополнительно: 
 =
= 
Просмотр содержимого презентации
«Решение уравнений, №1»
Решение уравнений 6класс — Математика
Открытый урок
по математике по теме: «Решение уравнений»
6класс
Провела: Паль О.В.
2016 год
Открытый урок по математике в 6 классе
Тема урока: «Решение уравнений»(слайд1)
Цели:
Образовательные:
закрепить знания, умения, навыки решения уравнений;
закрепить понятие корня уравнения, правило переноса слагаемого из одной части уравнения в другую, правила умножения или деления обеих частей уравнения на одно и то же число, отличное от нуля.
Развивающие:
развитие интеллектуальных умений: анализа алгоритма решения уравнения, условия задачи, логического мышления при построении алгоритма решения уравнения, вариативности выбора способа решения, систематизации уравнений по способам решения;
развитие качеств личности – трудолюбия, аккуратности, настойчивости в достижении дел;
развитие гибкости мышления, памяти, внимания и сообразительности;
развитие математической речи;
развитие зрительной памяти.
Воспитательные:
воспитание познавательной активности;
формирование навыков самоконтроля и самооценки;
привитие математической грамотности;
воспитание чувства товарищества, вежливости, дисциплинированности, ответственности, умения осуществлять совместную деятельность;
формирование честности, ответственности.
Задачи урока:
1. Научить переносить знания от одного предмета к другому.
2. Снять монотонность урока и перегрузку учащихся, повысить интерес к математике, используя для этого различные методы проведения урока на разных его этапах.
3. Закрепить навыки действий с рациональными числами.
4. Закрепить навыки раскрытия скобок.
5. Закрепить навыки приведения подобных слагаемых
6.Закрепить навыки решения уравнений.
Тип урока: комбинированный
Оборудование: доска; мультимедийный проектор; презентация к уроку для демонстрации через проектор «Решение уравнений. pps»
Ход урока:
I.Организационный момент.
Здравствуйте ребята и уважаемые гости!
Прозвенел уже звонок
Начинается урок
Мы сегодня не одни
Гости на урок пришли!
2.Сообщение темы и целей урока (слайд 2)
—
Альберт Эйнштейн
Альберт Эйнштейн, один из основателей современной физики, сказал: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения (предлагается ученикам продолжить мысль учёного)
будут существовать вечно».
Вот сегодня мы и будем с вами заниматься вечным – решать уравнения. На предыдущих уроках вы решали уравнения и сегодня мы продолжаем отрабатывать умение решать уравнения, повторяем теоретический материал по теме «Решение уравнений» тем самым готовимся к контрольной работе.
III. Устная работа. «Разминка».
Теоретическое повторение: за правильный ответ дается жетон.
Что называется уравнением?
Что называется корнем уравнения?
Что значит « решить уравнение»?
Сколько корней может иметь уравнение?
Алгоритм решения уравнений:
Шаг 1 | Посмотреть на уравнение | 2 (3x – 6) = 4 — 2x |
Шаг 2 | Раскрыть скобки, если это нужно сделать. | 6x – 12 = 4 — 2х |
Шаг 3 | Все слагаемые, содержащие неизвестное, переносим в левую часть, а известные в правую с противоположным знаком !! | 6х + 2х = 4 + 12 |
Шаг 4 | Приводим подобные слагаемые. | 8 x = 16 |
Шаг 5 | Делим обе части уравнения на коэффициент при неизвестном. | х = 2 . |
Шаг 6 | Не забудь написать ответ!!! | Ответ: 2. |





Ребята, разминка закончилась, давайте подведем итоги устной работы. Учащиеся подсчитывают полученные жетоны. Оценивание своей работы.
IV. Закрепление
У каждого ученика листочек для внесения ответов.
1.Упростить выражение из правой таблицы
и поставить ему в соответствие выражение из левой таблицы
А | —a — 10 | |||||
Б | -2t — 2 | |||||
В | -b | |||||
Г | 2t – 12 | |||||
Д | 2t — 1 | |||||
Е | -3a + 2 | |||||
1 | a + 2b – a – 3b |
2 | -2a + 5 – 3 — a |
3 | 8 – 4a + 3a -18 |
4 | 4t + 1 – 2t – 2 |
5 | 5 + 3t – 7 – 5t |
2.Найти уравнение, равносильное уравнению
2x — 6 = 5 – 7x
1 | 2x – 7x = 5 – 6 |
2 | 2x + 7x = 6 — 5 |
3 | 2x + 7x = 5 + 6 |
4 | -5x = 11 |
5 | 9x = 11 |
3.Найти уравнение, равносильное уравнению
-2x + 5 = 3 – 4x
1 | -2x + 4x = 3 — 5 |
2 | 2x + 4x = 3 + 5 |
3 | 2x + 4x = 5 — 3 |
4 | 2x = -2 |
5 | 6x = 2 |
4.Найти выражение,
равное выражению
-2( -3x + 2y -4)
1 | -6x + 4y -8 |
2 | 6x + 2y -4 |
3 | 6x — 4y + 8 |
4 | -6x — 4y -8 |
5 | 6x + 4y -8 |
5.Работа в парах
Ребята, а вы помните, когда первый раз решали уравнения?
А вы знаете, кто и когда придумал первое уравнение?
О тветить на этот вопрос невозможно. Ещё за 3-4 тысячи лет до н.э египтяне и вавилоняне умели решать простейшие уравнения. Греки унаследовали знания египтян, и пошли дальше. Наибольших успехов в развитии учения об уравнениях достиг греческий учёный Диофант (3 век), о котором писали:
тветить на этот вопрос невозможно. Ещё за 3-4 тысячи лет до н.э египтяне и вавилоняне умели решать простейшие уравнения. Греки унаследовали знания египтян, и пошли дальше. Наибольших успехов в развитии учения об уравнениях достиг греческий учёный Диофант (3 век), о котором писали:
Он уйму всяких разрешил проблем.
И запахи предсказывал, и ливни
Поистине, его познанья дивны.
В дальнейшем многие математики занимались проблемами уравнений. Одним из них был французский математик, фамилию, которого вы узнаете, если выполните задания, предложенные вам для работы в парах.
Каждому корню уравнения соответствует буква из таблицы.
Решите уравнение:
1) 6х – 12 = 5х
2) -2х + 3 = 5х – 4
3) 7у – 7 = 5у + 3
4) -4а + 8 = -5а + 4
И | Т | В | Е | Л | А |
1 | -4 | 12 | 5 | -7 | 10 |
Ответ: Виет
Учащиеся обмениваются тетрадями, проверяют по эталону на слайде.
Проверка
6х-5х=12 х=12 | 2) -2х + 3 = 5х – 4 -2х-5х=-3-4 -7х=-7 х=-7:(-7) х=1 |
3) 7у – 7 = 5у + 3 7у-5у=7+3 2у=10 у=10:2 у=5 | 4)-4а + 8 = -5а + 4 -4а+5а=-8+4 а=-4 |
Ответ: Виет
Ф рансуа Виет (1540-1603)
рансуа Виет (1540-1603)
Замечательный французский математик, положивший начало алгебре как науке о преобразовании выражений, о решении уравнений в общем виде, создатель буквенного исчисления.
Физкультминутка:
Быстро встали, улыбнулись,
выше-выше потянулись!
Вправо, влево повернулись,
рук коленями коснулись.
На носки, затем на пятки.
Лень отбросить и опять
Сесть за парту, взять тетрадку уравнения решать!
6.«Ромашка»
Учащимся предлагается решить уравнения, которые записаны на лепестках ромашки. Ответ зашифрован буквой. Расшифруйте.
1) 3х + 45 = 2х + 15 | 6) 5х + 4 = х – 12 | 11)4х-50=6-3х | 16) 8х – 5 = 10х + 3 |
2) – 8х = — 8 | 7) 7х + 3 = 3х + 11 | 12) 9х – 5 = х – 5 | 17) 2у – 3 = 3у – 1 |
3) 2х – 3 = 5 | 8) – 7х = 21 | 13) 10х -25 = 7х + 5 | 18) 7у + 9 = 3у – 7 |
4) 3х + 1 = х + 3 | 9) 3х – 8 = 2х – 1 | 14) 4х + 7 = 11 | 19) 2у + 4 = у + 6 |
5) 3х = — 18 | 10) 32х = — 16 | 15) 8х + 7 = 5х + 4 | 20) 16х = — 48 |
-30 | 7 | -4 | -6 | 4 | -2 | -3 | -0,5 | 0 | 8 | 10 | -1 | 2 | 1 |
Т | — | И | п | Р | Б | Ь | Д | Н | А | Е | ш | С | 0 |
1) 3х + 45 = 2х + 15, х=-30
2) – 8х = — 8, х=1
3) 2х – 3 = 5, х=4
4) 3х + 1 = х + 3, х=1
5) 3х = — 18, х=-6
6) 5х + 4 = х – 12, х=-4
7) 7х + 3 = 3х + 11, х=2
8) – 7х = 21, х=-3
9) 3х – 8 = 2х – 1, х=7
10) 32х = — 16, х=-0,5
11)4х-50=6-3х, х=8
12) 9х – 5 = х – 5, х=0
13) 10х — 25 = 7х + 5, х=10
14) 4х + 7 = 11, х=1
15) 8х + 7 = 5х + 4, х=-1
16) 8х – 5 = 10х + 3, х=-4
17) 2у – 3 = 3у – 1, х=-2
18) 7у + 9 = 3у – 7, у=-4
19) 2у + 4 = у + 6, у=2
20) 16х = — 48, х=-3
Торопись – да не ошибись. Ребята открывают ответы и составляют пословицу. Хором читают мудрую мысль.
V. Домашнее задание.
Повторить правила п.30,31
№849 стр.181
Подготовиться к контрольной работе.
Итог урока.
Спасибо за работу.
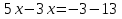
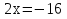
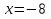
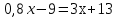
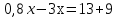
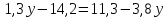 Верное решение:
Верное решение: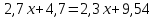
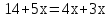
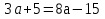
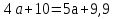
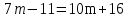
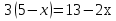
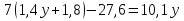
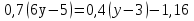
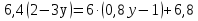
 (км/ч)
(км/ч)