Уравнение для 6 класса: Решение уравнений — урок. Математика, 6 класс. – УРАВНЕНИЯ — 6 КЛАСС — РАЗНОУРОВНЕВЫЕ ЗАДАЧИ ПО МАТЕМАТИКЕ — Каталог статей

Решение уравнений (Вольфсон Г.И.). Видеоурок. Математика 6 Класс

На этом уроке вы узнаете, какие свойства уравнений можно применять при их решении. Вы познакомитесь с определением линейного уравнения и уравнения, сводящегося к линейному. Разобранные примеры и упражнения проиллюстрируют применение рассмотренных правил и позволят связать новый и ранее изученный материал в единое целое.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Уравнения и неравенства»

Рассмотрим решение уравнения:

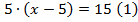
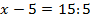
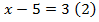
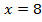
Уравнение (2) можно получить из уравнения (1), разделив обе части уравнения на 5.

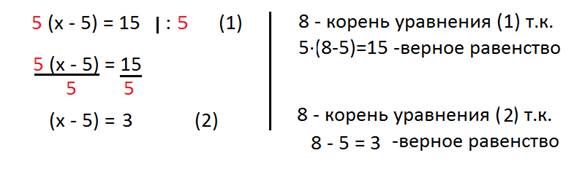
Число 8 – это корень уравнения (1) и корень уравнения (2).

Сформулируем первое свойство уравнения.

Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю, и корни уравнения не изменятся.

Пример 1.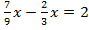

Умножим обе части уравнения на 9. Тогда коэффициент перед 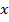 станет целым.

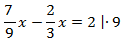
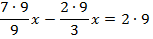
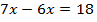
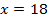
Ответ: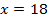

Пример 2.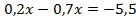

Умножим обе части уравнения на 10. Тогда коэффициенты перед 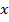 станут целыми.

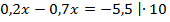
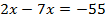
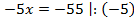
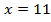
Ответ:

Пример 3.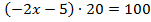

Разделим обе части уравнения на 20.

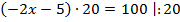
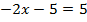
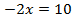
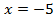
Ответ: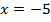

Пример 4.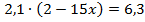

Разделим обе части уравнения на 2,1.

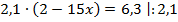
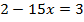
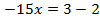
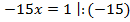
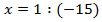
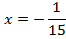
Ответ: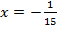

Рассмотрим решение уравнения:

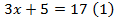
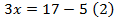
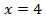
Число 4 – это корень уравнения (1) и корень уравнения (2).

Заметим, что уравнение (2) можно было получить, перенеся число +5 из левой части в правую с противоположным знаком:

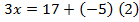
Сформулируем второе свойство уравнения:

Любое слагаемое можно перенести из одной части уравнения в другую, изменив при этом его знак на противоположный.

Рассмотрим решение еще одного уравнения: .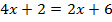

Вычтем из левой и правой части уравнения 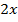. Тогда  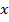останется только в левой части.

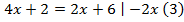
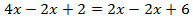
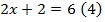
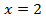
Число 4 – это корень уравнения (3) и корень уравнения (4).

Второе свойство уравнений можно сформулировать иначе.

Если к обеим частям уравнения прибавить одно и то же число, то корни уравнения не изменятся. Если из левой и правой части уравнения вычесть одно и то же число, то корни уравнения не изменятся.

Пример 1.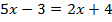  

Воспользуемся вторым свойством уравнений. Принято слагаемые, которые содержат неизвестное, собирать в левой части уравнения, а остальные в правой.

Пример 2.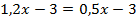  

Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.

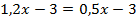
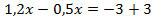
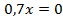
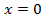
Пример 1.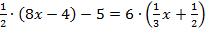  

Сначала раскроем скобки.

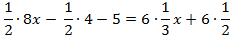
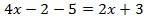
Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.

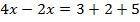
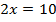
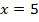
Пример 2.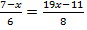

Воспользуемся основным свойством пропорции. Произведение средних равно произведению крайних.

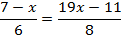
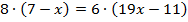
Раскроем скобки в левой и в правой части уравнения.

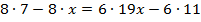
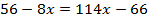
Перенесем неизвестное влево, а известное вправо.

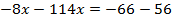
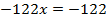
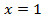
Во всех рассмотренных примерах мы приводили уравнение к виду

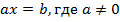
Уравнения такого вида называют линейными уравнениями с одним неизвестным. Уравнения, которые можно с помощью преобразований привести к такому виду, называют сводящимися к линейным.

При каких значениях переменной 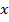 значение выражения  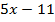равно значению выражения ?

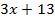Составим уравнение и решим уравнение.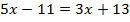

Перенесем неизвестное влево, а известное вправо.

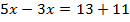
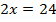
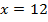
Ответ: при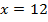

Условие. Рост мальчика – 75 см и еще половина его роста. Найдите рост мальчика.

Решение.

1. Пусть 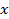 (см) – половина роста.

Тогда весь рост равен 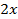 (см),

с другой стороны, весь рост – 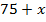 (см).

Составим уравнение:

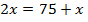
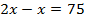
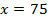
75 см – половина роста

2. 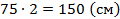 – весь рост мальчика

Ответ: 150 см.

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Математика (Источник).
2. Интернет-портал Math-portal.ru (Источник).

Домашнее задание

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012: № 1333, № 1342 (а, г, ж, л), № 1343.
2. Другие задания: № 1345, № 1347.

Урок по математике на тему «Уравнения» (6 класс)

Урок математики в 6 классе по теме «Уравнения»

Пояснительная записка

Данный урок проведен, по учебнику 6 класса для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С, И. Шварцбурд. — М.: Мнемозина, 2009.

Устная работа направлена на закрепление вычислительных навыков и подготовку к изучению новой темы.

Этот урок является первым из восьми отведенных на изучение данной темы. Главной целью является ознакомить учащихся новым способом решения уравнений с использованием свойств: умножение или деление обеих частей уравнения на одно и то же число и переносом из одной части уравнения в другую.

Данный урок построен в соответствии с принципами здоровьесбережения. Чередование видов деятельности (устный счет, фронтальная, групповая и индивидуальная работа) позволяют сохранить работоспособность детей на хорошем уровне в течение всего урока.

Класс: 6

Предмет: Математика.

Тема: Решение уравнений.

№ урока по данной теме: Первый.

Оборудование: Документ камера

Цель: Цели урока.

1. Образовательные:

• построить алгоритм решения уравнения методом группировки известных и неизвестных слагаемых;

• формирование умения пользоваться алгоритмом при решении уравнений.

2. Развивающие:

• формирование умения выделять главное, сравнивать, анализировать и делать выводы;

• формирование умения формулировать познавательные задачи, планировать познавательную деятельность;

• развивать качества личности – трудолюбие, аккуратность, настойчивость в достижении цели.

3. Воспитательные:

• выработка объективной оценки своих достижений;

• формирование честности, как составляющей законопослушания;

формирование ответственности Формирование умений и навыков решения простейших линейных уравнений при создании условий здоровьесбережения на уроке.

Воспитание взаимоподдержки в ходе совместной деятельности, настойчивости для достижения конечных результатов.

Ход урока

Начать урок словами Жен Жака Руссо «Вы — талантливые дети! Когда – нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремится к их достижению»

1. В тетради записать дату, классная работа.

2. На слайде Записи: 24х – 56х 5(4а — 7) – (12 + 24а) 16 х = 32 2у + 7у = 8,1 2,7n – (3,8 n – 14,8) 8x = 2x+18.

Разделите записи на две группы. По какому признаку вы это сделали?

2 ученика записывают на доске 2 столбика: (Вахрушева А, Лабутин Н)

1.Буквенные (Алгебраические) выражения

2 Уравнения.

А) Какие действия мы умеем выполнять с буквенными выражениями?

(раскрывать скобки, приводить подобные слагаемые) Упрощаем выражения на доске ( Бурдина, Маргунов, Мига)

Б) Уравнения – решаем самостоятельно. Проверка по готовому решению ученика( через документ камеру)

— Какие правила применяли для решения?

— Какое уравнение вызвало затруднения?

— Почему?

— Чем это уравнение отличается от тех, которые мы умеем решать?

(содержит неизвестное в обеих частях уравнения).

— Значит тема сегодняшнего урока: Уравнения, содержащие неизвестное в обеих частях

— Какова цель? — Научится решать уравнения

— Что для этого нужно нам сделать? — Вывести правило, которое не изменит корни уравнения, и позволит сделать так, чтобы неизвестные оказались в одной части.

— Запишем 1) сформулировать правило

2) применять правило.

— Какие правила, не меняющие корни уравнения мы знаем?

3. Пословица: Одна голова хорошо, а две лучше.

Как она относится к нашему уроку?

Работа в группах. (3 группы)

(Детям дается задание на карточках. Решают одну и туже задачу, но разными способами).

Один представитель от группы, выходит к доске и объясняет решение.

— Какую закономерность мы увидели во всех решенных уравнениях?

— неизвестное из правой части перешло в левую, только поменяло знак на противоположный.

— Изменились ли корни? Сформулировать правило. Проработать опорный конспект. ( работа в парах)

4. Вернемся к уравнению 8x = 2x+18. Чтобы его решить, что нужно сделать? (На доске решает Лабутин)

5. Закрепим правило при решении уравнения б) 1 – 5х = — 6х + 8.

Анализирум это уравнение, чем оно отличается от предыдущего, чем дополняем правило

__ Переносим не только неизвестные, но и известные, так, чтобы в левой части собрать – неизвестные, а в правой – известные.

Решаем на доске _ (Муленко)

6. Самостоятельно: 10х + 9 = 7х

у+ 2у + 20 = — 3у — 16 Проверка через документ камеру.

Оценочный лист

Фамилия,имя_____________________________________________________Поставьте знак « + », если вы не допустили ошибки при выполнении действия, и знак « — », если действие выполнено с ошибкой.

Критерии оценки

Уравнение № 1

Уравнение № 2

1. Получен правильный ответ

2. Правильно выполнен перенос слагаемых из одной части уравнения в другую

3. Правильно выполнено приведение подобных слагаемых

4. Отсутствуют вычислительные ошибки

Самооценка работы по критериям. Кто поставил себе 8 « + «, 7, 6 ,5 Молодцы. Обратите внимание на «-« и проработайте соответствующие правила.

7. Вернемся к цели урока. Достигли ли ее?

8. Необходимо еще раз закрепить полученные знания . Домашнее задание: п. 42, правило , 1342 (а, в, д, ж)

Уравнение из ГИА – 9 №1

Электронный дневник, группа «Готовимся к экзаменам»

9 Резерв.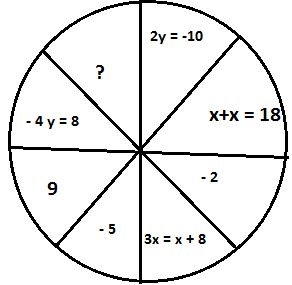

Логическая задача. Как найти неизвестное число?

— Нужно соотнести уравнение и его корни. Решить уравнение 3х = х

+ 8 и найденный корень и будет тем неизвестным, которое нужно найти х = 4.

10 Вернемся к эпиграфу урока. Кто выскажет свои мысли.

Приложения

Опорный конспект по теме «Решение уравнений».

● Если к обеим частям верного равенства прибавить или отнять одно и тоже число, не равное нулю, то получится верное равенство.

● Если обе части верного равенства умножить или разделить на одно и тоже число, не равное нулю, то получится верное равенство.

● Члены уравнения можно переносить из одной части в другую,

изменив их знак на противоположный.

Опорный конспект по теме «Решение уравнений».

● Если к обеим частям верного равенства прибавить или отнять одно и тоже число, не равное нулю, то получится верное равенство.

● Если обе части верного равенства умножить или разделить на одно и тоже число, не равное нулю, то получится верное равенство.

● Члены уравнения можно переносить из одной части в другую,

изменив их знак на противоположный.

Учебно-методический материал по математике (6 класс) на тему: Урок по математике для 6 класса на тему: «Решение уравнений и задач с помощью уравнений»

Урок по математике  для 6 класса на тему: «Решение уравнений и задач с помощью уравнений»

Тип урока: обобщающий урок.

Цель урока: повторение решений линейных уравнений с одной переменной и решение задач с помощью уравнений

Задачи:

Образовательная:  

— отработка навыка решения уравнений, задач с помощью уравнений;

— обобщение  и закрепление знаний по теме «Решение уравнений»;

— знакомство учащихся с некоторыми фактами из истории математики, привитие интереса к науке.

Воспитательная: 

воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов, воспитание культуры работы с товарищем, воспитание умения выслушивать и уважать мнение других.

Развивающая: 

развитие познавательного интереса, внимания, памяти, логического мышления, умения анализировать условие задачи, развитие потребности и навыка совместного поиска решения, развитие устной речи.

Ход урока:

1. Организационный момент.

Учитель приветствует учащихся, проверяет готовность к уроку. 

Встаньте. Улыбнитесь. Сегодня у нас много гостей, молодых учителей. Посмотрите на них. Какие эмоции передадим нашим гостям?
Положительные эмоции. Поделитесь капелькой теплоты, добра. Отрицательные эмоции мы оставляем вне школы. Садитесь. Почему в начале урока мы заговорила о положительных и отрицательных эмоциях? Изучили положительные и отрицательные числа.

2. Устный счет.

На каждом уроке мы повторяем некоторые приемы устного счета. Сегодня вспомним умножение двузначных чисел на 11, возведение в квадрат чисел, оканчивающихся на 5, и интересный способ умножения древних индийцев (воздушный счет). Карточки для устного счета: 62·11, 48·11, 352, 852, 93·98. За верные ответы поставьте 2б.

А теперь игра в парах «Крестики-нулики». Подведите итог игры. Запишите счет. Кто победил поставьте 2б, кто проиграл-1б.  

3. Постановка цели.

Посмотрите на ребусы. Отгадайте их (уравнение, задача).

 Сформулируйте тему урока. Решение уравнений и задач с помощью уравнений.

Уравнение пришло, 
Тайн немало принесло.

Сегодня завершающий урок по теме «Решение уравнений и задач с помощью уравнений». Какие задачи мы поставим? Учащиеся формулируют задачи урока. Повторить правила решения уравнений. Применять их при решении уравнений и задач.  Урок сегодня необычный – это итоговый урок по теме,  это  значит, что у каждого есть шанс заработать хорошие отметки. А для этого вы должны быть активны и внимательны. В конце урока гости определят самого активного, знающего, он получит приз зрительских симпатий – «5». Перед каждым на парте лежит рабочий лист с планом урока. По ходу урока вы должны будете его заполнить.

4. Проверка домашнего задания + актуализация знаний.

Стихотворение (читают 2 человека)

В стране поистине чудесной,

Что математикой зовут,

Однажды числам стало тесно.

И поднялся великий бунт.

В тоске огромной и печали

Весь числовой и прочий люд.

Им просто нужен был начальник,

Но где ж его они возьмут?

      И тут явился очень странный,

На вид приличный гражданин,

Ходил он всюду в черной маске

И был для всех неуловим.

О боже, кто же это может

Таким быть славным чудаком?

Тоска тебе уж сердце гложет,

Ты до сих пор с ним не знаком?!

Быть может это мафиози?                             А может сыщик из «Твин-пикс»?

Но все гораздо будет проще,                         Зовут его все «Мистер ИКС»!

Закройте глаза, представьте себе мистера Х. Какой он у вас? Какой разный мистер Х. А говорят, что математика – сухая наука.  А так изобразила его ученица 10А класса Полина.    

Что же хочет сказать он нам? На обратной стороне написано: «Задача из домашнего задания». Мистер Х  пришел к нам из домашней задачи. Он нам напоминает, что мы должны проверить решение. Прочитайте текст. Каким способом вы  решали? Алгебраическим.  С помощью уравнения. Кто такой Диофант? Его по праву считают «отцом алгебры». Он умел решать очень сложные уравнения (стр. 236 учебник)  

Задача. На памятнике древнегреческому математику Диофанту (III в), о котором мы говорили на прошлых уроках,  имеется надпись. “Прохожий! Под этим камнем покоится прах Диофанта умершего в старости. Шестую часть его жизни заняло детство, двенадцатую — отрочество, седьмую – юность. Затем он женился, и через 5 лет у него родился сын, который прожил вдвое меньше отца. 4 года до самой своей кончины Диофант оплакивал своего сына”. Сколько лет жил Диофант? (Ответ: 84) Решение задачи расскажет Никита Смирнов.  Поставьте Никите отметку и прокомментируйте. А теперь самооценка. Если задача решена верно, поставьте 5. Поднимите руку те, кто получил первую 5.    

5. Математическая физкультминутка.

Прав английский поэт средних веков Чосер, который сказал: «Посредством уравнений, теорем, он уйму разрешил проблем». Выучив правила решения уравнений, мы тоже разрешили уйму проблем. Сейчас мы проверим знания правил во время физкультминутки.

     Уравнения решали и немного мы устали.

А теперь мы отдыхаем, физминутку начинаем.

 Если вы согласны  с утверждением, то поднимаете руки вверх, если нет, то опускаете вниз. Исходное положение: руки на плечах.

1. Уравнение – это равенство, содержащее букву, значение которой надо найти (да).
2. Решить уравнение – это значит найти все его корни или убедиться, что корней нет (да).
3. Корень уравнения 0х = 2 равен 0 (нет).
4. Корнем уравнения называется значение буквы, при котором из уравнения получается верное числовое равенство (да).
5. Если перед скобками стоит знак «–», то нужно раскрыть скобки, сохранив знаки слагаемых (нет).
6. Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и  то же число, не равное 0 (да).
7.  Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, не изменив при этом знак (нет).
8. Если перед скобками стоит знак «+», то можно опустить скобки, сохранив знаки слагаемых (да).
9.  Произведение может быть равно нулю, когда хотя бы один из множителей равен нулю (да).  

Кто выполнял верно – поставьте 2б. Каких утверждений было больше: истинных или ложных?    На сколько?   На 3.    

5.  Решение уравнений.

 В среду мы подвели итоги игры «Математическое ралли». А 3  машины, на которых путешествовали 6 классы, до сих пор не в гараже. Решите уравнения и по найденным ответам узнайте, в каком гараже располагается каждая из данных машин. На доске картинки гаражей, на слайде картинки машин, а под ними уравнения. Решаем по колонкам.

-3х+15= -5х+21 (х=3)           17х-11=5х+1 (х=1)                  20х+8= -4х+56 (х=2)

Молодцы. Каждая машина свою работу выполнила и встала в гараж. А мы не всё выполнили.

Послушайте еще одно стихотворение и скажите, о чем оно?

                  Когда уравнение решаешь дружок,

                  Ты должен найти у него корешок.

                   Значение буквы проверить не сложно,

                   Поставь в уравнение его осторожно.

                  Коль верное равенство выйдет у вас,

                 То корнем значенье зовите тот час.

О проверке. Выполните проверку. Теперь мы уверены, что каждая машина в своем гараже. Первая машина едет в гараж № 3, вторая — № 2, третья — № 1.Учитель выдает машинки, и учащиеся ставят их в гаражи.  Те, кто верно решил  уравнение, поставьте 2б.      

6. Решение задач.

Машины вернулись с игры «Мат. ралли». Не могли они приехать с пустыми багажниками. Все они что – то прихватили. Посмотрим.

Меваер ларолкоякесьпо фацаги. Переведите с помощью тарабарской грамоты. Решаем самостоятельно задачи.

      7.   Самостоятельная работа.

Вариант 1

1. На одном садовом участке в 5 раз больше кустов малины, чем на другом. После того как с первого участка пересадили на второй 32 куста, на обоих участках кустов малины стало поровну. Сколько кустов малины было на каждом участке?
2. В двух мешках сахара было поровну. Если из первого мешка взять 30 кг, а из второго 10 кг, то в первом мешке останется в 2 раза меньше сахара, чем во втором. Сколько кг сахара было в каждом мешке?

Вариант 2

1. У двух братьев поровну орехов. Если старший брат отдаст младшему 10 орехов, то орехов у него станет в 5 раз меньше, чем у младшего. Сколько орехов у каждого брата?
2. На одной автостоянке было в 4 раза меньше машин, чем на другой. Когда со второй стоянки на первую перевели 12 автомобилей, машин на стоянках стало поровну. Сколько машин было на каждой стоянке первоначально?

Еще немного поработаем и будем подводить итоги.   

“Арифметика Магницкого”

Краткая историческая справка: Перед вами страница первого русского печатного учебника математики, получившего широкое распространение “Арифметики” Леонтия Филипповича Магницкого. Книга эта была издана в 1703 году. ( копия этой страницы висит на доске)

Вот что пишет автор: “Арифметика или числительница есть художество честное, независтное, всем удобопонятное, многополезнейшее и многохвалейнейшее.

На первой странице книги изображен дворец науки. На престоле сидит царевна “Арифметика”, в её правой руке символический ключ — это ключ ко всем знаниям. Без арифметики нет доступа к другим наукам, к познанию арифметики ведут пять ступеней: счисление, сложение, вычитание, умножение и деление. В первой части первой книги “Арифметика” изложена нумерация целых чисел и все действия с целыми числами, а во второй части рассматриваются числа ломанные, т.е. дроби.

Вот вам задача из этой книги (раздать карточки с задачей на каждый стол). Задача. Спросил некто учителя: “Сколько у тебя в классе учеников, т.к. хочу отдать к тебе в учение своего сына?”. Учитель ответил: “Если же придет учеников столько же, сколько имею, и половина, и четвертая часть класса, и твой сын, тогда будет у меня 100 учеников. Спрашивается, сколько учеников было у учителя?” (Ответ: 36)

Эту задачу вы решите дома. Запишите домашнее задание: задача из «Арифметики» Магницкого, № 1342(л, м)

В завершение слова Альберта Эйнштейна: “Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно”.

8. Рефлексия.

Кому мы можем сказать спасибо за урок?  Кого мы можем оценить? Почему? Кто помогал весь урок, вел за собой?  А теперь проанализируйте свою работу на уроке. Ответьте на вопросы: “Что нового я узнал на этом занятии? Что у меня получается хорошо при решении уравнений и решении задач на составление уравнений? Что получается плохо и почему?” Посчитайте количество баллов и поставьте себе отметку в рабочий лист. Отметка 5 – …  баллов, отметка 4 – …  баллов, отметка 3 – …  баллов. Встаньте те, кто получил 5. Молодцы. А теперь слово нашим гостям.

ПРИЛОЖЕНИЕ.

Рабочий лист.

«Решение уравнений и задач с помощью уравнений»

Ф. И.

1. Устный счет.
2. Проверка домашнего задания.
3. Математическая физкультминутка.
4. Решение уравнений.
5. Решение задач (самостоятельная работа).
6. Итог урока.

Конспект урока для 6 класса. Тема: «Решение уравнений»

Урок математики в 6 классе «Решение уравнений»

Тип урока: урок «открытия» новых знаний.

Цель: ввести понятие корня уравнения, ознакомить со свойствами уравнений и новым способом решения уравнений

Задачи

Образовательные: 1. Сформировать понятие корня уравнения.

2. Отработка навыков решения уравнений.

Развивающие: 1.Развивать познавательный интерес

2. Развивать внимание, память, речь.

Воспитательные: Воспитывать общую культуру, коммуникативность, самостоятельность, активность; умение работать в парах, группах.

Вид урока: проблемное обучение

План урока

1. Организационный момент

2. Мотивация

3. Актуализация знаний.

4. Открытие новых знаний.

5. Первичное закрепление.

6. Включение в систему знаний.

7. Самостоятельная работа.

8. Подведение итогов.

9. Рефлексия.

10. Домашнее задание.

Оборудование: компьютер, мультимедийный проектор, экран, карточки, контрольный тест на листах.

Ход урока

Организационный момент

Приветствие. Проверьте свою готовность к уроку. На месте ли тетрадь, учебник, дневник?

Мотивация.

— Пусть девизом нашего урока будут слова из «Поучения» великого князя Владимира Мономаха: «Что умеете хорошо не забывайте, а чего не умеете тому учитесь». (слайд 1)

Актуализация знаний.

Для начала (в соответствии с девизом урока) давайте проверим, не забыли ли вы изученное ранее.

Перечислите из чего состоят выражения (Выражения состоят из чисел, знаков арифметических действий, скобок, букв…) (слайд 2)

№1 (слайд 3)

Перед вами выражение: 5х+2-3х+2*(х-1)

Что можно сделать с этим выражением? (Упростить)

Предлагается упростить выражение. Один ученик проговаривает последовательность действий. Сначала раскрываются скобки, приводятся подобные слагаемые и т.д.

Получается 4x. Что такое 4? (Коэффициент)

Открытие новых знаний.

Упрощать выражение вы уже умеете. Примените свои знания при выполнении следующего задания. Оно поможет вам сформулировать тему урока.

1. Учитель: Перед вами анаграмма, нужно сложить из букв слово с помощью перестановок (слайд 4)

х + 6 = 11 х= 3 Р

20 – х = 17 х = 5 У

-2х + 7х +2 4а-5b Н

— 3( х – 5) х=-5 Н

4,4а + 5b — 0,4а – 10b -3х+15 В

2+х=5 5х + 2 А

— 6х = 30 х= 3 Е

3х+5+4х х= 4 Е

5х+20 7х+5 И

10x+3 = 8х + 5 ?

Ученики обсуждают ответ в группах. (Ответ: Уравнение).

Учитель: Значит, чем мы будем заниматься сегодня? (Уравнениями)

А что мы будем с ними делать? (Решать)

Назовите тему сегодняшнего урока? (Решение уравнений)

Запишите тему урока: «Решение уравнений» (слайд-5)

Давайте вспомним, что такое уравнение. (Это равенство, содержащее неизвестную)

Что значит решить уравнение? (Это значит найти такое число, при подстановке которого вместо х получается верное равенство.)

Как называется то значение неизвестного, при котором уравнение обращается в верное равенство? (Корнем уравнения)

Обратите внимание на наш экран (на доску). Вы видите, что одно уравнение осталось без пары. В чем его особенность? (Неизвестный стоит и в правой и левой части)

Вы попали в ловушку. Вы умеете решать такие уравнения? (Нет)

Хотите научиться?

Формулировка цели учениками.

Какую цель поставим сегодня на уроке?

Научиться решать уравнения, в которых неизвестный стоит и в правой и в левой части.

(Учитель записывает это выражение на доску)

Уравнения играют очень важную роль в математике. Поэтому, чтобы хорошо овладеть математикой, необходимо научиться решать уравнения. Многие процессы, происходящие в природе описываются уравнениями.

А.Эйнштейн как то сказал: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно». (слайд-6)

Ну а прежде, чем научиться решать уравнения, в которых неизвестный стоит и в правой и левой части, вспомним те уравнения, которые вы решать уже умеете. И обратим внимание на некоторые особенности этих уравнений.

Давайте решим уравнение 5(x-3)=20. Сколькими способами можно его решить? (Двумя способами: 1) Используя распределительное свойство; 2) по правилу нахождения неизвестного множителя) Разбираем оба способа решения. (слайд-7)

Работа с учебником

А теперь откройте учебник на стр.229 и прочитайте пример 1. Как в учебнике предлагается решить похожее уравнение? (слайд-8)

Первичное закрепление.

Всё ли понятно?

Прочитайте вывод (с.229)

Вывод: корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю. (слайд-9)

Таким образом, можно решить наше уравнение третьим способом. Что для этого надо сделать? (Разделить обе части на 5) (слайд-10)

Предлагается еще одно уравнение для закрепления: 3(х+5)=15

Работа с учебником

Теперь посмотрите в учебнике пример 2 на стр. 229.

Какой вывод можно сделать?

(Уравнения 2х+5=17 и 2х=17-5 имеют один и тот же корень) (слайд-11)

Вывод: корни уравнения не изменяются, если какое–нибудь слагаемое перенести из одной части в другую, изменив при этом его знак на противоположный. (слайд-12)

Приведу такой пример. Вы ходите по дому в домашней одежде. А чтобы выйти на улицу зимой вам надо одеться, т.е. изменить одежду. Представьте, что знак равенства – это дверь. Переходя через дверь, вы меняете одежду, а числа и буквы в уравнениях меняют знак.

Используя полученный вывод, решите уравнение: 6х=3х+9.

Что нужно сделать для решения этого уравнения? (перенести слагаемые с х в одну часть, не забыв поменять знак перед х, а в другой части оставить слагаемые без х)

А теперь мне кажется у вас достаточно знаний для того, чтобы решить наше уравнение, которое осталось без пары вначале урока 10х+3=8х+5. (слайд-13)

Историческая справка. Кто первым ввел понятие «уравнение»

Кто и когда придумал первое уравнение? Ответить на этот вопрос невозможно. Задачи, приводящие к решению уравнений, люди решали на основе здравого смысла. За 3-4 тыс. лет до н.э. египтяне и вавилоняне решали задачи с помощью уравнений. Только не умели применять буквы. Вместо букв брали числа, показывали на числах, как решать задачу, а потом все похожие решали тем же способом.

Теорией уравнений занимался древнегреческий ученый Диофант. (слайд-14)

Но по- настоящему, метод уравнений сформировался в руках арабских ученых. Первым написал книгу на арабском языке о решении уравнений Мухаммед ибн Мусса Аль — Хорезми. (слайд-15)

Включение в систему знаний.

Решение №1314 из учебника (выполняют со взаимопроверкой)

После проверяют полученные результаты с ответами, выведенными на экран проектора (доску) (слайд-16)

— А теперь немного отдохнем

Физкультминутка для глаз. Геометрические фигуры

Найдите в кабинете треугольник и обведите его глазами несколько раз (направление обхода показано стрелкой), затем найдите квадрат и круг и проделайте тоже самое

№ 1316 (а,б,в) с комментированием у доски

Проверка знаний

Самостоятельная работа (слайд-17)

Решите уравнения:

а) х+7=5

а) х+9=6

б) 2,8х=11,2

б) 3,6х=21,6

в) 3(х-3)=15

в) 4(х+5)=24

г) 2х+4=х+6

г) 3х+4=2х+6

— Возьмите друг у друга тетради и проверьте работу. Ответы выведены на экран проектора (слайд-18)

Оценка «5» — 0 ошибок

«4» — 1 ошибка

«3» — 2 ошибки

«2» — 3 и более ошибок

Подведение итогов

— Что нового вы узнали сегодня на уроке?

— Что такое корень уравнения?

Рефлексия (слайд 19)

— С каким настроением вы уходите с урока?

Мне всё удалось (кто с этим согласен сделайте хлопок в ладоши)

У меня остались вопросы (кто так считает, сделайте два хлопка)

Домашнее задание. (дифференцированное)

П.42, № 1341 (1 ст.), 1342 (а,ж), 1348(а). (слайд-20)

Доп. задание 1343.

Спасибо за урок! До новых встреч! (слайд-21)

План-конспект урока по математике (6 класс) на тему: Урок по теме «Решение уравнений» 6 класс

ТЕХНОЛОГИЧЕСКАЯ КАРТА

урока по математике

«Решение уравнений»

Цель: формировать навык решения уравнений при решении различных задач; формировать умение формулировать собственное мнение; формировать умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах.

Планируемые результаты

Предметные: решать основные виды линейных уравнений; выполнять вычисления с рациональными числами, выполнять тождественные преобразования рациональных выражений, решать уравнения по алгоритму, решать текстовые задачи арифметическим способом;

 Метапредметные: совершенствовать умения взаимодействовать друг с другом, слушать и слышать других; контролировать процесс и результат учебной деятельности; оценивать результат своей учебной деятельности, интерес к изучению темы; желание применить на практике свои знания; адекватно воспринимать оценку учителя и одноклассников.

Личностные УУД: формирование устойчивой мотивации к обучению на основе алгоритма выполнения задачи; формирования осознанного выбора наиболее эффективного способа решения, ответственное отношение к учению, готовности и способности к саморазвитию и самообразованию на основе мотивации к обучению и познанию, осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению.

Регулятивные УУД: корректировать деятельность: вносить изменения в процесс с учетом возникших  трудностей и ошибок, намечать способы их устранения; обнаруживать учебную проблему, составлять план выполнения работы; выстраивать последовательность необходимых операций (алгоритм действий).

Коммуникативные УУД: адекватно использовать речевые средства для представления результата.

Познавательные УУД: использовать приобретённые знания для развития учебных достижений.

Тип урока: урок открытия новых знаний.

Оборудование:

Учебник Математика:6 класс: учебник для учащихся общеобразовательных учреждений/А.Г. Мерзляк, В.Б.Полонский, М.С.Якир.-М.:Вентана –Граф,2016.

Презентация.

мультимедийный проектор;

раздаточный материал. 

Материал по алгебре (6 класс) по теме: Таблица целей решение уравнений 6 класс

Презентация к уроку по алгебре (6 класс) на тему: Тема урока : «Решение уравнений». 6 класс.

Тема урока: « Решение уравнений»

Цель урока: создание благоприятных условий для развития творческой и мыслительной деятельности учащихся через исследовательский подход к изучению нового материала.

Задачи урока.

Образовательные: 

1. Изучить свойства решения уравнений, ввести определение линейного уравнения, отрабатывать навыки решения линейных уравнений.

Развивающие:

1.Способствовать развитию самостоятельности, способности видеть проблему, анализировать, обобщать, делать выводы, ясно и четко излагать свои мысли.

2.Развивать логику мышления.

Воспитательные:

1.Воспитывать интерес к знаниям и предмету математики.

2. Воспитывать чувство взаимопомощи, дружбы.

Оборудование: доска, мультимедиа-комплекс.  

Дидактические средства:

1. математика-6 (Н.Я. Виленкин , В.И.Жохов,  А.С.Чесноков, С.И.Шварцбурд),  

М.: Мнемозина, 2011.

2. http://www.matematika-na.ru/6class/mat_6_42.php Математика 6 класс. Задачи. Тесты. Решение уравнений
3. рабочие листы.
4. презентация.

Тип урока: урок усвоения новых знаний.

1. Мотивация. (2 мин)

Учитель.

Открывает электронную почту и видит письмо от царицы «Математики». В письме билет в страну «Знаний».

Учитель. Сообщается тема урока «Решение уравнений» ( презентация)

Целью нашего путешествия будет исследование новых способов решения уравнений, знакомство с линейным уравнением и практическая работа, связанная с применением новых свойств решения уравнений. ( презентация)

Каждый из вас должен потрудиться, чтобы достичь цели и вернуться из путешествия с новым запасом знаний.

2. Подготовка к изучению нового материала. (5 мин)

(подготовка к путешествию)

Перед тем как отправиться за новыми знаниями,  давайте проверим, как мы готовы их усваивать. Выполним несколько заданий на повторение с комментированным ответом.

№1. Раскройте скобки.

а) у + (х + с – z) – вспомнить правило раскрытия скобок, если перед скобкой стоит знак  «+»

б)  – ( 3х + 4у ) — вспомнить правило раскрытия скобок, если перед скобкой стоит знак  «-»

в)   5(а – 4b) – вспомнить правило раскрытия скобок, если перед скобкой множитель.

№2. Укажите коэффициент

а) 0,6х· 5у        б)   — 0,5 · 2а          в)  — а · 1,5b – вспомнить определение коэффициента.

№ 3. Приведите подобные слагаемые.

а) 7х – 5у +4х +3у             б) 6х – 8у + 2х – вспомнить определение подобных слагаемых.

3. Изучение нового материала

Инструктаж (1 мин)

1.Теперь можно отправляться в путь. А вот и наша звезда, которая нас быстро доставит в страну знаний.

Пока мы преодолеваем путь,  я проведу инструктаж по ходу исследовательской работы, которую  нам предстоит выполнить. Вы разбиты на три группы. Каждая группа имеет 2 консультантов, которые направляют работу группы, контролируют и помогают выполнить задание всем остальным учащимся. У вас на столах  рабочие листы на которых указан номер группы, ознакомьтесь с ним.  Рабочий лист разбит на 4  столбца. В первом столбце сформулирован теоретический вопрос, на который вы должны дать ответ во втором столбце, используя ресурс, указанный в четвёртом столбце. Третий столбец включает в себя практическое задание которое вы должны выполнить после того как исследуете теоретический вопрос.

2.Итак, ребята мы прибыли в страну «Знаний». Посмотрите, на карте есть город  «Уравнения».  Нам нужно в него попасть. (презентация: город закрыт и чтобы в него опасть нужно решить уравнение), учитель  решает уравнение на доске используя комментарий учащихся, уравнение решено , ребята попадают в город «Уравнений», где им предстоит отыскать новые свойства решения уравнений, учитель предлагает взять рабочие листы и начать исследовательскую работу по первому заданию, ребята работают, учитель направляет ,помогает).

 Учитель решает уравнение на доске используя комментарии учащихся.

( 1 мин)

4(х + 5) = 12

Вопросы учащимся:

-укажите неизвестный множитель?                    (х + 5) = 12 : 4

— как найти неизвестный множитель?                   х + 5 = 3

— чем является неизвестное?                                   х = 3 — 5

— как найти неизвестное слагаемое?                       х =  -2

— как называют число -2?                                          Корень уравнения.

1 этап исследовательской работы

Это уравнение можно решить другим способом и вы его должны исследовать самостоятельно используя ресурс указанный в рабочем листе. Возьмите рабочие листы и найдите теоретическое задания 1  , прочитайте, посмотрите, какой ресурс вашей группе предложен и начинайте работу, если с теоретическим заданием справитесь, приступайте к практическому заданию,  все записи и решения выполняете в рабочем листе.

Ребята работают   (2 мин)

1 группа.

Рабочий лист ученика 6 класса

Тема урока: «Решение уравнений»

2,3 группы.

Рабочий лист ученика 6 класса

Тема урока: «Решение уравнений»

Обсуждение результатов 1 этапа (3 мин).

1.Учитель предоставляет слово каждой группе, они освящают вопрос (как его подготовили) и делают общий вывод. (Слайд презентации)

2.Учитель обращает внимание учащихся на ранее решённое уравнение и предлагает использовать новый метод решения. (Слайд презентации)

4(х + 5) = 12

4(х + 5): 4 = 12: 4

х + 5 = 3

х = -2

3.Учитель предлагает рассмотреть решение практического задания, с этой целью предоставляет его прокомментировать одной из групп, затем показывает правильное решение (слайд презентации).

Также продолжается работа над вторым вопросом.

2 этап исследовательской работы

Учитель объясняет решение уравнения. (Слайд презентации) (2 мин)

5х = 2х + 6

Вычтем из обеих частей уравнения по 2х

5х – 2х = 2х -2х + 6

5х – 2х = 6

3х = 6

х = 2

Ответ: х = 2

Это уравнение можно решить другим способом, используя второе свойство уравнений. Найдите это свойство, используя предлагаемый ресурс. Сделайте записи в рабочем листе и постарайтесь выполнить практическое задание.

Ребята работают   (2 мин)

Обсуждение результатов 2 этапа (3 мин).

1.Учитель предоставляет слово каждой группе, они освящают вопрос (как его подготовили) и делают общий вывод. (Слайд презентации)

2.Учитель обращает внимание учащихся на ранее решённое уравнение и предлагает использовать новый метод решения. 

Решим уравнение, используя 2 свойство уравнений  (презентация)

5х = 2х + 6

5х – 2х = 6

3х = 6

х = 2

3.Учитель предлагает рассмотреть решение практического задания, с этой целью предоставляет его прокомментировать одной из групп, затем показывает правильное решение (слайд презентации).

Физкультминутка. (2 мин)

3 этап исследовательской работы

Работа учащихся  (2 мин)

1.Ребята записывают в рабочих листах определение линейного уравнения.

2. Выполняют практическое задание.

Обсуждение  (3мин)

1.Формулируют определение линейного уравнения.

2.Делают общий вывод. (Слайд презентации)

3.Проверяется практическое задание. (Слайд презентации)

Подводится итог исследовательской работы.(1мин) 

Ребята возвращаются в родную школу.

4.Закрепление. (12мин)

Решение упражнений у доски.

№ 1316 (а, б)

№ 1317 (а, б)

№ 1321 (задача)

5. Итог урока.

1.Выставление оценок. (Слайд презентации) (1 мин)

2.Домашнее задание.  п.42, №1341 (а, б, в),1342(а, б, в, г) , презентация на тему (1 мин)

«Свойства, используемые при решении уравнений».

http://interneturok.ru/ru/school/matematika/6-klass/undefined/reshenie-uravnenij

6. Рефлексия. (2 мин)

Выбери верное утверждение.

1. Обе части уравнения умножили на число, не равное 0.

Корни уравнения не изменились.

2. Обе части уравнения разделили на число, не равное 0.

Корни уравнения  изменились.

3. Слагаемое перенесли из одной части уравнения в другую,

изменив при этом  его знак. Корни уравнения не изменились.

4. Слагаемое перенесли из одной части уравнения в другую,

изменив при этом  его знак. Корни уравнения  изменились.

Карточку готовых ответов прикрепляют к доске с помощью магнита .