Уравнения 6 класса по математике: Решение уравнений — урок. Математика, 6 класс. – УРАВНЕНИЯ — 6 КЛАСС — РАЗНОУРОВНЕВЫЕ ЗАДАЧИ ПО МАТЕМАТИКЕ — Каталог статей

Тренажёр по математике (6 класс) по теме: Математика для 6 класса. Карточка — тренажор. Решение уравнений

По теме: методические разработки, презентации и конспекты

Презентация к уроку математики в классе — комплекте (5,6 класс) по теме «Решение уравнений и задач при помощи уравнений»

Презентация составлена к уроку математики в 5 и 6 классах по теме: «Решение уравнений и задач при помощи уравнений» в классе — комплекте сельской малокомплектной школы….

урок математики в 5 классе по теме «Решение уравнений» (заседание клуба «Серьезных математиков»)

на уроке в игровой форме учащиеся закрепляют знания о взаимосвязи между компонентами арифметических действий, на основе этих знаний отрабатывают умения решать уравнения…

Интегрированный урок в 9 классе математика+ физика «Применение математических методов решения уравнений 2-й степени при решении физических задач».

Интегрированный урок в 9 классематематика+ физика«Применение математических методов решения уравнений 2-й степени при решении физических задач».     Разработали:  учитель…

РАЗРАБОТКА УРОКА ПО МАТЕМАТИКЕ В 5 КЛАССЕ НА ТЕМУ «РЕШЕНИЕ УРАВНЕНИЙ И ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ»

Урок проводится в форме игры на основе сказки «Колобок». Класс делится на 3 команды.ЦЕЛИ:Систематизировать, закрепить навыки решения уравнений.Воспитать чувство взаимопомощи, умение преодолевать трудн…

Конспект по математике 2 класс на тему: «Решение уравнений»

Конспект по математике 2 класс на тему: «Решение уравнений&quot…

Дидактические материалы для занятий математического кружка «Математика +» 7 класс. Занятие32-34. Решение уравнений с модулем

Математический кружок- одна из наиболее эффективных форм внеклассных занятий. Для меня, как учителя, важно иметь под рукой пособие, в котором представлены идеи решений и которое позволило бы провести …

Урок по математике для 6 класса на тему: «Решение уравнений и задач с помощью уравнений»

Урок по математике  для 6 класса на тему: «Решение уравнений и задач с помощью уравнений&raquo…

Презентация к уроку по математике (6 класс) на тему: Решение уравнений 6 класс

Слайд 1

На какие две группы можно разделить? 5( x – 3) = 20 x + 8 = – 15 7,5s – 3k 5x = 2x +6 a – 4 + b 4b 6m – 1

Слайд 3

Тема урока : Решение уравнений Тема урока:

Слайд 4

Разгадайте анаграмму и определите, какое слово лишнее? зачада лиратерату варунение извененаяст ЗАДАЧА ЛИТЕРАТУРА УРАВНЕНИЕ НЕИЗВЕСТНАЯ

Слайд 5

Решите устно уравнения 3x = 15 1 5 – x = 8 + x = 1 8 ,6 x : 3 = 1,2 10 — 5x = 3 6x – 14 = 4 7x — 54 = 2 4,9 — x = 0

Слайд 6

Вспомни Что называется уравнением ? Что называется корнем уравнения? Что значит решить уравнение?

Слайд 7

Решите уравнения 1) 1,5+2,5х=14 2) (х-1,1)-2=5 3) 10-0,3х=6,4 4) х:100-20=7,2

Слайд 8

Найди ошибку 1) (30-х)+12,5=17,4 2)(0,2х+7):0,5=16,4 30-х=17,4+12,5 0,2х+7=16,4*0,5 30-х=29,9 0,2х+7=8,2 х=30-29,9 0,2х=8,2-7 х=0,1 0,2х=1,2 х=1,2:0,2 х=0,6

Слайд 9

Исторический экскурс Кто придумал уравнения? Ответить на этот вопрос невозможно! Задачи, приводящие к решению простейших уравнений, люди решали на основе здравого смысла. Еще 3-4 тысячи лет до нашей эры египтяне и вавилоняне умели решать простейшие уравнения, вид которых не был похож на современные. Греки унаследовали знания египтян, и пошли дальше. Наибольших успехов в развитии учения об уравнениях достиг греческий ученый Диофант ( IIIв ) “Он уйму всяких разрешил проблем. И засухи предсказывал и ливни. Поистине его познанья дивны”

Слайд 10

Это интересно Первым написал книгу на арабском языке о решении уравнений среднеазиатский ученый Мухаммед ибн Муса ал-Хорезми (IX век) . Название у нее было очень странное – «Краткая книга об исчислении ал– джабры и ал– мукабалы ». В этом названии впервые прозвучало известное нам слово «алгебра».

Слайд 11

Ал — джабра При решении уравненья Если в части одной, Безразлично какой, Встретится член отрицательный, Мы к обеим частям, С этим членом сличив, Равный член придадим, Только с знаком другим,- И найдем результат нам желательный.

Слайд 12

Ал — мукабала Дальше смотрим в уравненье, Можно ль сделать приведенье, Если члены в нем подобны, Сопоставить их удобно, Вычтя равный член из них, К одному приводим их.

Слайд 13

Физминутка

Слайд 18

Удивительное сравнение можно сделать, основываясь на математических понятиях. Решите уравнение и определите кому принадлежат слова: “Человек — есть дробь. Числитель — это, сравнительно с другими, достоинства человека, знаменатель — это оценка человеком самого себя. Увеличить своего числителя — свои достоинства, не во власти человека, но всякий может уменьшить своего знаменателя — свое мнение о самом себе, а этим уменьшением приблизить к совершенству»… (2 х+3):0,5=50 А.С.Пушкин x = 11 0 Л.Н.Толстой x = 11 С. Есенин x = 1 ,1

Слайд 19

Самостоятельная работа. Вариант 1. Вариант 2. Реши уравнения: х + 32 = 171 463 – у = 219 (246 + а) – 42 = 643 Реши уравнения: 83 + с = 345 n – 93 = 139 318 – (т – 8) = 27 В санатории было 97 отдыхающих. После того, как несколько человек уехало на экскурсию, в санатории осталось 78 отдыхающих. Сколько человек уехали? В автобусе было 78 пассажиров. На остановке несколько человек вышли. В автобусе осталось 59 пассажиров. Сколько человек вышли из автобуса на остановке?

Слайд 20

Ответы к самостоятельной работе 1 вариант 2 вариант 1) х=139 1) с=262 2) y=244 2) n=232 3) а=439 3) m=299 4) 19 ЧЕЛОВЕК 4) 19 ЧЕЛОВЕК

Слайд 21

Выберите слово, которое у вас ассоциируется с содержанием прошедшего урока Успех Польза Новизна Интерес Лёгкость Скука Трудность Бесполезность

Слайд 22

Спасибо за урок

Презентация по математике «Решение уравнений» (6 класс)

Технологическая карта урока

Данные об учителе: Масленникова Нина Семеновна, высшая категория, МБОУ «СОШ№ 39», г. Владивостока, Приморского края.

Предмет: математика Класс: 6 Учебник (УМК): Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 6 класс: Учебник для общеобразовательных учреждений. — М.: Мнемозина, 2014.

Тема урока: Решение уравнений

Тип урока: урок изучения нового материала

Оборудование: доска, мультимедийное оборудование.

Характеристика учебных возможностей и предшествующих достижений учащихся класса, для которого проектируется урок:

Учащиеся владеют

• регулятивными УУД:

— формулировать вопросы по теме на основе опорных (ключевых и вопросительных) слов;

• познавательными УУД:

• выделять и структурировать информацию, существенную для решения проблемы, под руководством учителя;

• личностные УУД:

У учащихся недостаточно сформированы:

• коммуникативные УУД:

Цели урока как планируемые результаты обучения, планируемый уровень достижения целей:

проявлять интерес к новому содержанию, осознавая неполноту своих знаний

Познавательные УУД:

формулировать информационный запрос

Регулятивные УУД:

определять цели учебной деятельности

Ориентировоч-ный этап

Организовать самостоятельное планирование и выбор методов поиска информации,

Беседа

Фронталь-но-индиви-дуальная

Задает вопрос о способах получения нового знания, необходимого для ответа на возникшие вопросы, предлагает способ и последовательность действий

Называют известные им источники и методы поиска информации и знакомятся с предложенной учителем последовательностью действий

Регулятивные УУД:

планировать, т.е. составлять план действий с учетом конечного результата.

структурировать знания;

Коммуникативные УУД:

вступать в диалог, с достаточной полнотой и точностью выражать свои мысли.

Предметные УУД:

давать определения новым понятиям темы;

называть способы решения уравнения.

Практический этап

• обеспечить осмысленное усвоение и закрепление знаний

Практи-ческая работа

Индиви-дуальная, фронталь-ная

1. Дает задание для учащихся №1, организует обсуждение результатов ее выполнения.

2. Помогает впомнить понятия «уравнение», «равенство»; «корень уравнения».

3. Дает задание для учащихся № 2, организует обсуждение ее результатов.

1. Выполняют задания, сообщают о результатах.

2. Слушают объяснение учителя.

3. Выполняют задания № 2, сообщают о результатах.

Предметные УУД:

Различать способы решения уравнений, правильно формулировать ход решения уравнений, находить неизвестные компоненты, применять на практике полученные выводы

Познавательные УУД:

анализировать и сравнивать объекты, подводить под понятие;

Рефлексивно-оценочный этап

• осмысление процесса и результата деятельности

Беседа,письменное высказывание

Индиви-дуальная, фронталь-ная

1. Предлагает оценить факт достижения цели урока: на все ли вопросы найдены ответы.

2. Предлагает каждому учащемуся высказать свое мнение в виде предложения — телеграммы

1. Оценивают степень достижения цели, определяют круг новых вопросов.

2. Выборочно высказываются, делятся друг с другом мнением

Регулятивные УУД:

констатировать необходимость продолжения действий

Познавательные УУД:

решать различные виды уравнений

Коммуникативные УУД:

адекватно отображать свои чувства, мысли в речевом высказывании

Ход урока

Организационный этап

2 минуты

Учитель приветствует учащихся, проверяет их готовность к уроку.

Учащиеся готовы к началу работы.

Этап актуализация знаний.

5 минут

Учитель: Новые знания нам будет очень трудно осваивать без умения быстро и верно считать, поэтому, как всегда, начнем урок с устного счета:

1.Решить уравнения устно:

А) х+9=27; Б) 15+у=30; В) b – 7 = 14; г) у:20 = 3;

Д) 60-с = 18; Е) 10k =15; Ж) 5х=65; з) 2х+3=15-х

2. Открываем тетради, записываем число, классная работа.

-Обратите внимание на записи.

На доске: 4(а-5)=16; a-4+b; x+10=-5; 4b; 7,5s-3k; 6у=4у+8; 6m -1.

— Внимательно их изучите и ответьте на вопросы.

— На какие две группы можно разделить написанное?

— Как можно назвать каждую из групп?

— Интересна ли для нас 1 группа: выражения?

— А вторая? Почему?

– Кто догадался, какая тема сегодняшнего урока?

— Исходя из названия темы, давайте сформулируем цель нашего урока.

— Для того чтобы достичь цели урока, какие задачи нам надо поставить?

— Где можно узнать информацию по данной теме?

1.Решают в уме, один из учеников проговаривает ответ

2. Делают записи в тетради.

3.Учащиеся внимательно смотрят на записи, отвечая на вопросы:

1. На уравнения и выражения

2. Уравнения, выражения

3. Нет

4. Да, потому что уравнения можно решить.

4. Ребята объявляют тему урока и записывают в тетради: «Решение уравнений».

5. Формулируют цель: познакомиться с разными видами уравнений; научиться их решать.

6. Формулируют задачи:

1. вспомнить основные понятия, свойства, которые можно отнести к уравнениям;

2. изучить материал учебника по этой теме;

3. внимательно слушать учителя;

4. делать необходимые записи в тетрадях

7. Называют источники информации: учебник, учитель

Этап изучение нового материала

12 минут

1.Подготовительный этап.

– Что значит «решить уравнение»?

– Итак, уравнение – это равенство. А в жизни мы

встречаемся с понятием равенство?

Актуализация и постановка проблемы.

– Давайте посмотрим. Весы находятся в равно-

весии. Что произойдет, если с одной чаши весов убрать

груз?

– А что надо сделать, чтобы весы снова оказались в

равновесии?

– Это свойство «весов» нам еще пригодится.

— Давайте вернемся к началу нашего урока. В тетрадях запишем 1 уравнение и решим его. Какие существуют способы решения данного уравнения?

— Хорошо! Давайте сначала решим уравнение, применив распределительное свойство умножения:

1 способ

4(а-5) = 16

4а-20=16

4а=16+20

4а=36

а=36:4

а=9

— А сейчас по правилу отыскания неизвестных компонентов

2 способ

4(а-5) = 16

— Что неизвестно в уравнении?

— Как найти неизвестный множитель?

а-5=16:4

а-5=4

а=4+5

а=9

-Что мы получили в итоге?

— Что называется корнем уравнения?

-Число 9 является корнем уравнения а-5=4

и уравнения 4(а-5) = 16, так как 9-5=4 и 4(9-5)=16.

— Как из первого уравнения можно получить второе?

Мы с вами убедились, что корнем этих двух уравнений является одно и то же число. Поэтому:

Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и тоже число , не равное нулю.

2. Снова вернемся к началу урока и теперь рассмотрим второе уравнение: x+10= — 5. Как его можно решить?

Это уравнение решается с использованием зависимостей между компонентами и результатами математических действий. Но изучение отрицательных чисел дает возможность решить эти уравнения иначе.

— Вспомним, чему равна сумма противоположных чисел?

— Как можно получить в левой части уравнения только x?

— Рассмотрим решение этих уравнений.

x+10= — 5

x+10-10= -5-10

x=-15

— Мы видим, что слагаемые без переменной перешли из левой части уравнения в правую с противоположным знаком.

— А сейчас рассмотрим третье уравнение и решим его:6у=4у+8

— Чем данное уравнение отличается от предыдущего?

— Как его можно решить?

— Нужно получить такое уравнение, чтобы слагаемые с x были только слева. Что для этого необходимо сделать?

6у=4у+8

6у+ (-4у) = 4у+8+ (-4у)

6у+ (-4у) = 8

2у=8

у=8:2

у=2

Если число или неизвестное переносим из одной части в другую, мы должны поменять знак.

Корни уравнения не изменяются, если какое – нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.

1. Отвечают на вопросы:

1)Найти все значения

неизвестных, при которых оно обращается в верное равен-

ство или установить, что таких значений нет.

2) Называют возможные варианты, например, при взвешивании

3) Чаша с гирями перевесит.

4) Убрать гири или вернуть груз на место.

5. Записывают уравнение в тетрадях, предлагают варианты решения.

6)Вспоминают распределительное свойство умножения и решают уравнение в тетрадях, комментируя вместе с учителем ход решения.

7)Отвечают на вопросы: Множитель

8)Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

9) Корень уравнения а=9

Корнем уравнения называют то значение неизвестного, при котором это уравнение обращается в верное равенство

10) Это уравнение можно получить, разделив обе части данного уравнения на 4 или умножив обе части на 1\4.

11) Записывают в тетрадях вывод.

2.

1)Записывают уравнение в тетрадях, предлагают возможные варианты, решая уравнение

2) Нулю

3)Прибавить или отнять числа, противоположные числам в левой части.

4) Неизвестное есть и в правой и в левой части уравнения.

5) Предлагают варианты решения уравнения

6) Для этого надо к обеим частям уравнения прибавить (-4у). Решают уравнение

7) Записывают в тетрадях вывод.

Этап первичное осмысление и закрепление знаний

10 минут

1. — Принято при решении уравнений переносить слагаемые так, чтобы в левой части уравнения были неизвестные числа, а в правой — известные числа.

Решить №1314 и 1315 с комментированием на месте.

— Решают в тетрадях, один из учеников комментирует решение с места

Динамическая пауза

2 минуты

Мы славно потрудились и славно отдохнем.

Учитель называет предметы. Если называет одушевленные предметы дети встают, а если неодушевленные – сидят. Учитель читает: «Стол, трактор, кукла, заяц, трава, дождь, воробей, туман, самолёт, тигр, солнце, медведь».

Выполняют упражнение

Этап закрепление изученного материала

10 минут

Решить уравнение №1316( а- г) на доске и в тетрадях, проговаривая правила.

3. Решить уравнение №1319(а;б) с комментариями на месте.

1)Осмысливают и приступают применять новый способ решения на практике.

2)Делают записи в тетрадь. После выполнения задания сверяют с доской. Один из учеников решает у доски с комментарием.

3)Решают самостоятельно, сверяют с доской, один из учеников решает у доски.

Этап подведение итогов. Домашнее задание.

3 минуты

Рефлексия

1 минута

-Наш урок подходит к концу, сначала запишем домашнее задание, затем подведем итоги.

— На доске: Домашнее задание: п. 42, выучить правила; решить №1342(а; б; в; г) – на оценку «3», №1346 – на оценку «4», №1349– на оценку «5»

— Ваши вопросы по домашнему заданию.

— А теперь подведем итоги: Что мы хотели узнать? Что мы узнали? На все ли вопросы мы получили ответы?

— Давайте еще раз вспомним определение уравнения, корня уравнения.

— Итог урока каждый из вас подведет с помощью телеграммы; то есть в виде одного предложения, которое выразит ваше отношение к уроку.

Знаю … , понимаю …, умею применять.

1) Ребята записывают домашнее задание в дневниках.

2) Просматривают домашнее задание, задают вопросы

3)Проводят самоанализ, отвечают на вопросы; вспоминают правила; определение уравнения, корня уравнения.

4) В конце своей работы каждый ученик пишет телеграмму. По желанию зачитывают на весь класс

Самоанализ

Этапы урока

Уровень достижения планируемого результата

Возможные риски

Коррекционная работа

Стадия Вызова

Регулятивные действия

— Целеполагание как способность соотносить то, что уже известно и усвоено, и то, что еще неизвестно

— Планирование как определение последовательности промежуточных целей с учетом конечного результата

Познавательные действия

— Самостоятельное выделение и формулирование познавательной цели

— Выделение наиболее важной информации

— Построение логической цепочки вопросов

Коммуникативные действия

— Включаемость в коллективное обсуждение вопросов

— Постановка вопросов

Личностные действия

— Развитие познавательных интересов, учебных мотивов

Предметные действия

-Воспроизведение (актуализация) знаний об уравнениях

-Определение понятий «уравнение», «равенство», «корень уравнения»

— Определение основных направлений

в изучении темы

1. Ученики не видят, по какому принципу можно сгруппировать записи на доске.

2. Ученики не могут ответить на вопросы.

3. Ученики не могут сформулировать цель и задачи урока

1. Предложить рассмотреть каждую запись в отдельности, затем сравнить их, тем самым находя отличия и схожести.

2. Учитель на один из вопросов отвечает сам, показывает на своем примере как можно ответить.

3. Можно подсказать с помощью наводящих вопросов.

Стадия Содержания

Регулятивные действия

— Оценка как выделение и осознание того, что уже освоено и что еще подлежит усвоению, осознание качества и уровня усвоения

— Волевая саморегуляция как способность к мобилизации сил и энергии

Познавательные действия

— Поиск и выделение необходимой информации

— Выбор способа действия

— Умение осознанно строить речевое высказывание в письменной форме

Коммуникативные действия

— Умение слушать и вступать в диалог

— Инициативное сотрудничество в поиске и сборе информации

Личностные действия

— Развитие познавательных интересов, учебных мотивов

Предметные действия

— Построение нового знания об уравнениях

— Анализ информации по теме «Решение уравнений»

1. Ученики не могут привести примеры из жизни, где встречаются равенства

2. Ученики не умеют делать краткие записи (записывают целые предложения), на что уходит много времени

3. Ученики не знают, как применять полученные знания на практике.

1. Учитель может привести один из примеров, с которым сталкиваемся повседневно.

2. Потренировать учеников сворачивать информацию на отдельных предложениях

3. Еще раз обсудить задание, вспомнить правила и разобрать один из примеров.

Стадия Рефлексии

Регулятивные действия

— Оценка как выделение и осознание того, что уже освоено и что еще подлежит усвоению, осознание качества и уровня усвоения

Познавательные действия

Умение осознанно строить речевое высказывание в устной форме

— Выделение и формулирование познавательной цели

Коммуникативные действия

— Включаемость в коллективное обсуждение вопросов

— Постановка вопросов

— Умение аргументировать свою точку зрения

Личностные действия

— Оценка действий человека

-Развитие познавательных интересов, учебных мотивов

— Предметные действия

— Применение знаний об уравнениях при решении практических заданий

— Способность использовать полученные знания на практике

1. Ученики затрудняются с помощью одного предложения выразить свои мысли и подвести итог своей работы.

2. Ученики не хотят читать получившиеся «телеграммы»

3. Ученики не знают, где именно искать информацию по данной теме, если возникнут затруднения при выполнении домашней работы

1. Привести пример, выслушать тех учеников, которые справились с заданием.

2. Дать возможность послушать остальных, либо сдать в письменной форме

Учебно- методическое обеспечение

Основная литература.

1. Учебник: Математика. 5, 6 класс. / Н.Я. Виленкин, В.и. Жохов / М. Мнемозина, 2013г.

2. Методическое пособие для учителя «Математика 5 – 6 класс» / Н.Я. Виленкин

Дополнительная литература:

А.С.Чесноков, К.И. Нешков Дидактические материалы по математике для 5класса

А.С.Чесноков, К.И. Нешков Дидактические материалы по математике для 6класса

Технические средства обучения:

1. Компьютер

2. Мультимедийный проектор

3. Экран

Интернет-сайты для математиков

Тема урока: Решение уравнений 6 класс

Тема урока: Решение уравнений 6 класс

На этом уроке вы узнаете, какие свойства уравнений можно применять при их решении. Вы познакомитесь с определением линейного уравнения и уравнения, сводящегося к линейному. Разобранные примеры и упражнения проиллюстрируют применение рассмотренных правил и позволят связать новый и ранее изученный материал в единое целое.

 Первое свойство уравнений. Иллюстрирующий пример. Формулировка

Рассмотрим решение уравнения:

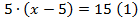
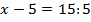
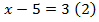
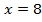Уравнение (2) можно получить из уравнения (1), разделив обе части уравнения на 5.

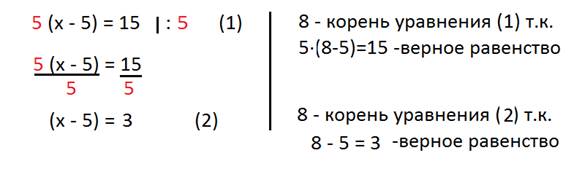Число 8 – это корень уравнения (1) и корень уравнения (2).

Сформулируем первое свойство уравнения.

Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю, и корни уравнения не изменятся.

 Применение первого свойства уравнений. Упражнения

Пример 1.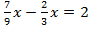Умножим обе части уравнения на 9. Тогда коэффициент перед  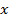станет целым.

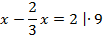
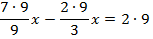
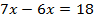
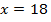
Ответ: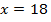 

Пример 2.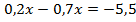Умножим обе части уравнения на 10. Тогда коэффициенты перед  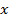станут целыми.

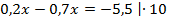
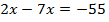
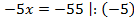
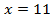Ответ: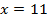 

Пример 3.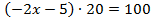 Разделим обе части уравнения на 20.

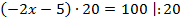
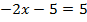
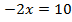
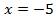
Ответ: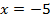 

Пример 4.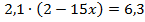 Разделим обе части уравнения на 2,1.

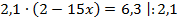
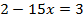
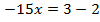
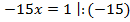
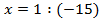
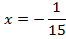
Ответ: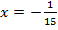 

 Второе свойство уравнений. Иллюстрирующие примеры. Формулировки

Рассмотрим решение уравнения: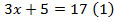

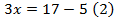
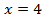Число 4 – это корень уравнения (1) и корень уравнения (2).

Заметим, что уравнение (2) можно было получить, перенеся число +5 из левой части в правую с противоположным знаком: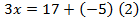

Сформулируем второе свойство уравнения:

Любое слагаемое можно перенести из одной части уравнения в другую, изменив при этом его знак на противоположный.

Рассмотрим решение еще одного уравнения: 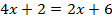.Вычтем из левой и правой части уравнения 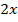. Тогда  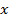останется только в левой части.

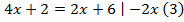
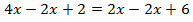
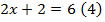
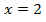Число 4 – это корень уравнения (3) и корень уравнения (4).

Второе свойство уравнений можно сформулировать иначе.

Если к обеим частям уравнения прибавить одно и то же число, то корни уравнения не изменятся. Если из левой и правой части уравнения вычесть одно и то же число, то корни уравнения не изменятся.

 Применение второго свойства уравнений. Упражнения

Пример 1. 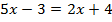 Воспользуемся вторым свойством уравнений. Принято слагаемые, которые содержат неизвестное, собирать в левой части уравнения, а остальные в правой.

Пример 2. 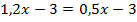 Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.

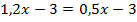
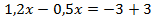
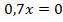
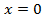
 Примеры решения более сложных уравнений

Пример 1.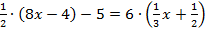  

Сначала раскроем скобки.

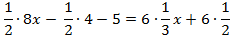
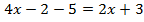Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.

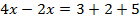
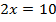
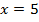
Пример 2.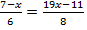 

Воспользуемся основным свойством пропорции. Произведение средних равно произведению крайних.

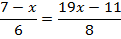
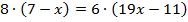
Раскроем скобки в левой и в правой части уравнения.

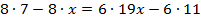
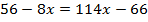
Перенесем неизвестное влево, а известное вправо.

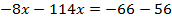
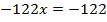
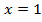
 Линейные уравнения. Определение

Во всех рассмотренных примерах мы приводили уравнение к виду

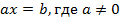Уравнения такого вида называют линейными уравнениями с одним неизвестным. Уравнения, которые можно с помощью преобразований привести к такому виду, называют сводящимися к линейным.

 Упражнение

При каких значениях переменной 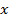 значение выражения  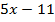равно значению выражения ?

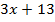Составим уравнение и решим уравнение.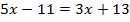 

Перенесем неизвестное влево, а известное вправо.

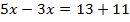
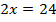
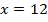
Ответ: при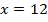 

 Текстовая задача

Условие. Рост мальчика – 75 см и еще половина его роста. Найдите рост мальчика.

Решение.1. Пусть 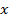 (см) – половина роста.Тогда весь рост равен  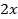(см),

с другой стороны, весь рост – 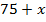 (см).

Составим уравнение:

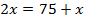
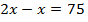
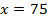
75 см – половина роста

2. 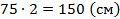 – весь рост мальчика

Ответ: 150 см.

План-конспект урока по математике (6 класс) на тему: Открытый урок уравнения 6 класс математика

Открытый урок в 6 А классе по теме «Уравнения».

(Подготовила учитель математики МОУ « СОШ №40» Саушкина Л.Н.

Тип урока: урок объяснения нового материала.

Цели: ввести понятие корня уравнения; ознакомить со свойствами уравнений и новым способом решения уравнений, с решением задач нового типа; отрабатывать умение решать уравнения; развивать грамотную математическую речь; развивать логическое мышление, налаживание дружественных, партнерских отношений.

1.Организационный момент.

Цель: включение учащихся в деятельность на личностно – значимом уровне.

Самопроверка домашнего задания, настрой детей на работу, ознакомление с планом урока.

2. Актуализация знаний.

Цель: повторение изученного материала, необходимого для открытия «нового знания». Слайд 1.

Расшифруйте анаграмму и узнайте тему урока.

.

1)3x-x                      4)2m+1-m                   7)3-2(6-y)

2)y-2.1y                   5)x-5-x                        8)3(x-1)+5

3)3-x+2                    6)2(5+x)+5 9)3-4m+10m

Итак, сегодня мы с вами решаем уравнения. Запишите, пожалуйста, тему урока «Уравнения».  Слайд 2.

Великий Энштейн говорил (Слайд 3): «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».

Возникновение проблемной ситуации.

1.Подготовительная работа.

-Какое равенство называют уравнением?

-Что значит решить уравнение?

-Какое значение неизвестного называется корнем уравнения?

Сегодня мы будем решать уравнения, используя их свойства.

1)5(х-3)=20                    2)х-3=4

х=7                               х=7

-Сравните эти два уравнения.

Как из первого уравнения получить второе? (Второе уравнение можно получить из первого делением на5 или умножением на1/5)

-Какой вывод из этого наблюдения можно сделать?

-Корни уравнения не изменятся если обе части уравнения разделить или умножить на одно и то же число.

3)2/3х+1/2=5/6

-Как удобнее всего решить это уравнение?  (умножить обе части на 6).

-Эти уравнения решались с использованием зависимостей между компонентами.

-Попробуем решить такое уравнение:

4)6х=3х-4

-Можем ли мы решить это уравнение, используя компоненты?

3.Постановка учебной задачи.

Цель: обсуждение затруднений.

— Почему мы не можем решить это уравнение?  (Неизвестное в обеих частях уравнения)

4. « Открытие нового знания»

-Вернемся к решению уравнения 1.

— Что произошло со слагаемым -15?

-Что произошло со знаком этого слагаемого?

-Посмотрите,как менялись знаки слагаемых во2 и 3 уравнениях?

-Какой вывод можно сделать? (Корни уравнения не изменятся, если  слагаемое перенести  из одной части уравнения в другую, изменив при этом его знак)

-Как эти знания нам помогут решить уравнение 4?( Перенести 3х из правой части уравнения в левую часть)

— Попробуем закрепить это знание, решив уравнение 5)5-3х=4-х.

5.Первичное закрепление.

Цель: закрепление нового знания. Налаживание деловых, партнерских отношений.

Способ: Коллективная работа в группах.

Каждая группа из 4-х человек  работает с четырьмя уравнениями (Слайд 4). Постепенно (по часовой стрелке) меняясь тетрадями. Затем каждый проверяет уравнения,записанные в своей тетради и сверяет с правильным решением. ( Слайд 5). Результаты заносятся в специальную таблицу. Все решенные уравнения проговариваются с комментированием: дети проговаривают правила в громкой речи. (Можно работать только с соседом по парте).

6. Физкультминутка

-Все встали, потянулись вверх на цыпочках, подняв руки. Опустили руки. Выполнили  вращательные  движения головой   по часовой,  затем против часовой стрелки. Заняли свои места.

7. Самостоятельная работа. (Слайд 6)

Цель: каждый для себя делает вывод о том, как он научился применять полученные знания.

Решить уравнения.

Вариант 1                                                                 Вариант 2

1. 4(2х-1)=20                                                            1) 3(3х-2)=12
2. 6х=4х-12                                                                2) 8х=5х+9
3. 2(х-1)=4х-12                                                           3)8(х-2)=3х-9

Работа выполняется письменно с дальнейшим самоконтролем и самооценкой . Ответы даются на доске. Слайд 7

8.Включение нового знания  в систему знаний и повторение.

 Работа с учебником.

Выполнение упражнений №1317(а,б), №1320(а)

9.Рефлексия деятельности (итог урока).

.

Цель: осознание учащимися  своей учебной деятельности.

-Какую цель ставили?

-Удалось ли решить поставленную задачу?

Домашнее задание №1342(а-в),1350,1351.

Тренажер по теме «Решение уравнений» 6 класс

Вариант 1

Вариант 2

Вариант 3

Решите уравнение

Решите уравнение

Решите уравнение

1) 15x + 10 = 6x − 8

1) 10x — 11 = 4x − 7

1) 11x + 15 = 7x − 25

2) -2(x − 4) = 3 + 7x

2) 14x − 25 = 20x + 9

2) 16x − 28 = 8x − 44

3) 26x − 6 = 8x − 42

3) -3(5 — x ) = 35 — 5x

3) 4x − 15 = — 7( 9 + x)

4) 10x − 8 = 20x + 74

4) 14x + 3 = 8x — 43

4) 17x − 8 = 20x + 9

5) 13x + 8 = 27x + 18

5) 18x + 9= 32x + 14

5) 21x + 24 = 34x + 3

6) 1,2(x − 4) + 4,6 = 0,3(3 + x)

6) 0,8(x − 2) + 2,6 = 0,5(7 + x)

6) 1,6(x − 2) + 3,4 = 0,7(4 + x)

7) —0,6(x − 3) − 3,3 = 0,6(4 − x)

7) —0,5(x − 4) − 7,3 = 0,8(2 − x)

7) —0,3(x − 9) − 4,8 = 0,3(5 − x)

8) х — 3 _{_} 5

х + 5 ¯ 8

8) х + 7 _ 3

х + 9 ¯ 4

8) х + 4 _ 9

х — 6 ¯ 2

9) х — 3 _{_} х + 8

5 ¯ 4

9) х — 7 _{_} 4 — х

9 ¯ 7

9) х + 5 _{_} —х + 2

3 ¯ 5

10) 7 _{_} 6

х + 8 ¯ 2 — х

11) 3 _{_} 2

х — 7 ¯ 4 — х

10) 7 _{_} 8

5 — х ¯ 2 + х

11) (9y − 2)( 2,1 − 7y ) = 0

11) (1,2x − 2)(8x + 5,6) = 0

11) (−5y − 1,5)(0,3y + 6,3) = 0

12) (−2x − 8,4)(0,7x + 4,2) = 0

12) (8y + 6)(1,8 − 0,4y) = 0

12) (15x − 1)(6x + 1,2) = 0

Вариант 1

Вариант 2

Вариант 3

Решите уравнение

Решите уравнение

Решите уравнение

1) 15x + 10 = 6x − 8

1) 10x — 11 = 4x − 7

1) 11x + 15 = 7x − 25

2) -2(x − 4) = 3 + 7x

2) 14x − 25 = 20x + 9

2) 16x − 28 = 8x − 44

3) 26x − 6 = 8x − 42

3) -3(5 — x ) = 35 — 5x

3) 4x − 15 = — 7( 9 + x)

4) 10x − 8 = 20x + 7

4) 14x + 3 = 8x — 43

4) 17x − 8 = 20x + 9

5) 13x + 8 = 27x + 18

5) 18x + 9= 32x + 14

5) 21x + 24 = 34x + 3

6) 1,2(x − 4) + 4,6 = 0,3(3 + x)

6) 0,8(x − 2) + 2,6 = 0,5(7 + x)

6) 1,6(x − 2) + 3,4 = 0,7(4 + x)

7) —0,6(x − 3) − 3,3 = 0,6(4 − x)

7) —0,5(x − 4) − 7,3 = 0,8(2 − x)

7) —0,3(x − 9) − 4,8 = 0,3(5 − x)

8) х — 3 _{_} 5

х + 5 ¯ 8

8) х + 7 _ 3

х + 9 ¯ 4

8) х + 4 _ 9

х — 6 ¯ 2

9) х — 3 _{_} х + 8

5 ¯ 4

9) х — 7 _{_} 4 — х

9 ¯ 7

9) х + 5 _{_} —х + 2

3 ¯ 5

10) 7 _{_} 6

х + 8 ¯ 2 — х

11) 3 _{_} 2

х — 7 ¯ 4 — х

10) 7 _{_} 8

5 — х ¯ 2 + х

11) (9y − 2)( 2,1 − 7y ) = 0

11) (1,2x − 2)(8x + 5,6) = 0

11) (−5y − 1,5)(0,3y + 6,3) = 0

12) (−2x − 8,4)(0,7x + 4,2) = 0

12) (8y + 6)(1,8 − 0,4y) = 0

12) (15x − 1)(6x + 1,2) = 0

Карточки по математике на тему «Уравнения» 6 класс