Математические диктанты. Числовые примеры. Все типы задач. Устный счет. 3 класс (Е. А. Нефедова, 2014)
1. Какие числа надо перемножить, чтобы получить 12?
2. Сколько будет, если взять 2 раза по 5?
3. Сколько будет: 5 троек?
4. Запиши число, которое меньше 8 на 2.
5. Запиши число, которое меньше 8 в 2 раза.
6. Сколько пятёрок в числе 10?
7. Сколько четвёрок в числе 12?
8. Умножь 3 на 3.
9. В одном стручке 5 фасолин. Сколько фасолин в трёх таких стручках?
10. Для работы на пришкольном участке 15 мальчиков разделились на 3 равные бригады. Сколько мальчиков было в каждой бригаде?
11. Уменьшаемое 53, вычитаемое 36. Найди разность.
12. Я задумал число, умножил его на 4 и получил 8. Какое число я задумал?
13. На столе лежали ложки, вилки и ножи. Ножей было 4. Вилок было в 3 раза больше, чем ножей, а ложек на 3 больше, чем ножей. Сколько вилок и ложек лежало на столе?
14. На полке стояли книги. Книг в синих обложках было 3, книг в зелёных в 5 раз больше, а книг в серых столько, сколько книг в синих и зелёных обложках вместе. Сколько книг в серых обложках стояло на полке?
15. Мальчик должен расставить 15 стульев около трёх столов поровну. Сколько стульев он поставит у каждого стола?
1. Какие числа надо перемножить, чтобы получить 14?
2. Сколько будет, если взять 3 раза по 4?
3. Сколько будет: 6 четвёрок?
4. Запиши число, которое меньше 7 на 3.
5. Запиши число, которое меньше 8 в 4 раза.
6. Сколько двоек в числе 8?
7. Сколько троек в числе 15?
8. Умножь 6 на 2.
9. В одной коробке 7 карандашей. Сколько карандашей в двух таких коробках?
10. 16 апельсинов поровну раздели между восьмью ребятами. По сколько апельсинов получил каждый?
11. Уменьшаемое 46, вычитаемое 29. Найди разность.
12. Я задумал число, умножил его на 3 и получил 15. Какое число я задумал?
13. На крыше сидели голуби, вороны и воробьи. Ворон было 7. Голубей было в 2 раза больше, чем ворон, а воробьёв на 4 больше, чем ворон. Сколько голубей и воробьёв было на крыше?
14. На полке 4 пакета вишнёвого сока, пакетов томатного сока в 3 раза больше, а пакетов яблочного сока столько, сколько пакетов вишнёвого и томатного вместе. Сколько пакетов яблочного сока стояло на полке?
15. В 3 вазы расставили поровну 21 цветок. Сколько цветков поставили в каждую вазу?
Работа над ошибками
1. 1) Какие числа надо перемножить, чтобы получить 12?
2) Какие числа надо перемножить, чтобы получить 16?
3) Какие числа надо перемножить, чтобы получить 18?
2. 1) Сколько будет, если взять 2 раза по 6?
2) Сколько будет, если взять 3 раза по 3?
3) Сколько будет, если взять 2 раза по 7?
3. 1) Сколько будет: 6 троек?
2) Сколько будет: 7 двоек?
3) Сколько будет: 5 четвёрок?
4. 1) Запиши число, которое меньше 10 на 2.
2) Запиши число, которое меньше 9 на 3.
3) Запиши число, которое меньше 6 на 2.
5. 1) Запиши число, которое меньше 10 в 2 раза.
2) Запиши число, которое меньше 9 в 3 раза.
3) Запиши число, которое меньше 6 в 2 раза.
6. 1) Сколько двоек в числе 10?
2) Сколько троек в числе 9?
3) Сколько четвёрок в числе 8?
7. 1) Сколько четвёрок в числе 16?
2) Сколько пятёрок в числе 15?
3) Сколько троек в числе 12?
8. 1) Умножь 4 на 3.
2) Умножь 3 на 2.
3) Умножь 5 на 2.
9. 1) В одной упаковке 6 фломастеров. Сколько фломастеров в трёх таких упаковках?
2) В одном наборе 4 заколки. Сколько заколок в трёх таких наборах?
3) В одной книге 6 листов. Сколько листов в трёх таких книгах?
10. 1) 21 гвоздику разделили на 3 равных букета. Сколько гвоздик в одном букете?
2) Между семью девочками разделили 35 киви. Сколько киви получила каждая девочка?
3) Разлили в 10 банок 30 л молока. Сколько литров молока в каждой банке?
11. 1) Уменьшаемое 73, вычитаемое 38. Найди разность.
2) Уменьшаемое 53, вычитаемое 16. Найди разность.
3) Уменьшаемое 84, вычитаемое 57. Найди разность.
12. 1) Я задумал число, умножил его на 3 и получил 9. Какое число я задумал?
2) Я задумал число, умножил его на 2 и получил 8. Какое число я задумал?
3) Я задумал число, умножил его на 4 и получил 12. Какое число я задумал?
13. 1) Бабушка сделала 6 блинчиков с вареньем, с творогом в 2 раза больше, чем блинчиков с вареньем, а с мясом на 2 блинчика больше, чем с творогом. Сколько блинчиков с творогом и с мясом сделала бабушка?
2) На празднике Ваня пустил в небо 5 красных шаров, синих в 3 раза больше, а зелёных на 3 больше, чем синих. Сколько синих и зелёных шаров пустил в небо Ваня?
3) Дети сделали 3 гирлянды, бумажных фонариков в 5 раз больше, а снежинок на 5 больше, чем фонариков. Сколько всего фонариков и снежинок сделали дети?
14. 1) На полке 4 словаря, задачников в 5 раз больше, а хрестоматий столько, сколько словарей и задачников вместе. Сколько хрестоматий на полке?
2) В концерте участвовало 6 мужских хоров, женских в 3 раза больше, а детских столько, сколько женских и мужских хоров вместе. Сколько детских хоров участвовало в концерте?
3) У бабушки 3 пачки грузинского чая, цейлонского в 2 раза больше, чем грузинского чая, а индийского чая столько, сколько грузинского и цейлонского чая вместе. Сколько пачек индийского чая у бабушки?
15. 1) Расставили поровну в 3 стакана 9 зубных щёток. Сколько зубных щёток в каждом стакане?
2) Вложили в 9 книг 18 закладок. Сколько закладок в каждой книге?
3) Разложили в 4 подарка 20 сюрпризов. Сколько сюрпризов в каждом подарке?
Умножение и деление. Видеоурок. Математика 3 Класс
Если вы хотите в уме научиться умножать и делить круглые трёхзначные числа, тогда вам повезло, ведь именно на этом уроке вы сможете это сделать. Если вы не знаете или знаете, но плохо, как умножать и делить круглые трёхзначные числа, тогда этот урок разработан специально для вас. Как здорово уметь быстро считать, делать вычисления на умножение и деления! Пока все думают, вы уже будете знать ответ.
На этом уроке мы рассмотрим два основных приёма: представления числа в качестве суммы разрядных слагаемых и представление числа в виде сотен или десятков. Также вспомним, как решаются примеры способом проверки. Вы точно проведёте время с пользой. Вперёд к успеху и знаниям!
И оценка, и почет –
Всем, кто любит устный счет!
Отточи свои уменья
В умноженье и деленье!
Способ нужный выбирай –
Быстро, весело считай!
Умножение и деление круглого трёхзначного числа на однозначное число легко заменить сотнями и десятками.
1. 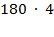 2.
2. 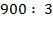
Решение: 1. Заменим число 180 десятками:
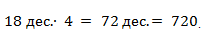
2. Во втором примере заменяем число 900 сотнями:
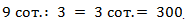
Познакомимся с другим приёмом устных вычислений и решим примеры. Вспомним правило умножения суммы на число.
При умножении суммы на число необходимо каждое слагаемое умножить на это число, а полученные произведения сложить.
Вспомним правило деления суммы на число.
При делении суммы на число необходимо каждое слагаемое разделить на это число, а полученные частные сложить.
1. 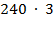 2.
2. 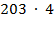 3.
3. 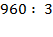 4.
4. 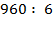
Решение: 1. Раскладываем число 240 на составляющие и проводим вычисления:
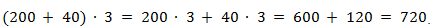
2. Заменим первый множитель во втором примере суммой разрядных слагаемых и найдём произведение:
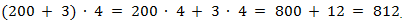
3. Проделаем тот же приём, только для нахождения частного:
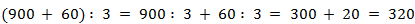
4. Повторим операцию на последнем примере, только здесь заменим делимое не разрядными слагаемыми, а удобными слагаемыми:
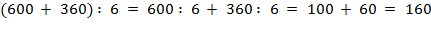 .
.
Можно воспользоваться и другим методом умножения и деления трёхзначных чисел на однозначное число.
1. 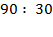 2.
2. 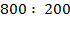
Решение: 1. Если мы делитель умножим на три, получим делимое девяносто.
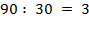 .
.
2.Возьмем двести четыре раза и получим восемьсот – делимое, следовательно, подбор осуществлён правильно.
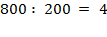 .
.
Если не получается подобрать правильный ответ с первого раза, необходимо продолжать подбирать числа до полного соответствия результатов.
Реши примеры на рисунке 1.

Рис. 1. Примеры
Решение: 1. В первом и во втором примерах заменим первые числа сотнями:
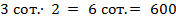
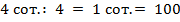 .
.
2. В третьем и четвёртом примерах воспользуемся приёмом разложения на разрядные слагаемые:
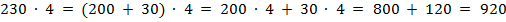
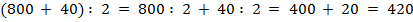
3. В последней паре примеров используем для решения метод подбора:
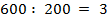 , проверка
, проверка 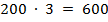
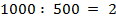 , проверка
, проверка 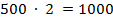 .
.
Список литературы
- Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012. – 112 с.: ил. – (Школа России).
- Рудницкая В.Н., Юдачёва Т.В. Математика, 3 класс. – М.: ВЕНТАНА-ГРАФ.
- Петерсон Л.Г. Математика, 3 класс. – М.: Ювента.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Festival.1september.ru (Источник).
- Samouchka.com.ua (Источник).
- Internat-sokol.umi.ru (Источник).
Домашнее задание
- Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012., ст. 82 № 1–3, ст. 83 1, 3, ст. 84 1, 2.
- Вычисли разными способами
а) б)
б) 
в) г)
г) 
- Вычисли методом подбора
а) в)
в) 
в) г)
г) 
- *В одну столовую привезли 40 банок огурцов по 5 кг в каждой, а в другую 50 банок по 3 кг в каждой. Сколько всего килограммов огурцов (рис. 2) привезли в две столовые?

Рис. 2. Огурцы (Источник)
Конспект урока по математике «Умножение и деление на 3.»
Тема: Умножение и деление на 3.
Цель: повторение и закрепление таблицы умножения и деления.
Задачи:
— закреплять приёмы сложения и вычитания в пределах сотни;
— закреплять знание таблицы умножения и деления на 3;
— продолжать развивать вычислительные навыки , закрепляя умения решать примеры и задачи .
— корректировать логическое мышление через решение примеров и простых задач;
— корректировать связную устную речь через правильно выстроенные, полные ответы на уроке.
— воспитывать дисциплинированность, активность, чувство взаимопомощи, мотивацию к учению.
I.Орг. момент.
Речевая зарядка.
Долгожданный, дан звонок
Начинается урок!
Начинаем мы опять
Считать, отгадывать, писать
Пожелаю вам удачи —
За работу! В добрый час.
Рапорт дежурного. Сегодня….
-Мы пришли сюда учиться
Не лениться, а трудиться
Слушаем внимательно
Работаем старательно
—На уроке мы с вами будем:
повторять;
считать;
решать примеры;
решать задачу;
работать с геометрическим материалом;
заработать хорошую отметку;
работать дружно.
II. Актуализация знаний.
1.-Какую тему проходим, мы узнаем, решив примеры:
3:3, 6:3, 3х1, 12:3, 15:3, 3х2, 3+4, 2х4, 3х3, 2х5
-Какую цифру мы открыли? (3) А как вы думаете ,почему мы сегодня говорим о числе три? Как оно связано с нашим уроком? (тема урока «Умножение и деление на 3».)
-У нас сегодня необычный урок. Мы отправимся в путешествие. Куда мы полетим узнаем, когда выполним задание
2. Расположите числа по порядку от меньшего к большему. Теперь перевернём карточки. (работа в группах, у каждого на парте карточки с цифрами)
73, 33, 13, 3, 43, 53
-Какое слово получилось?( космос)
-Значет мы с вами будем космонавтами и полетим в космос.
-Кто первым полетел в космос?(Юрий Гагарин)
-Зачем человек летает в космос? (изучает космос, луну, солнце, звезды, разные планеты: космонавты фотографируют Землю, помогают рыбакам узнать, где много рыбы, предупреждают где может случиться наводнение, пожар).
Работа космонавтов очень нужная и важная.
— Каким должен быть космонавт? (смелым, закаленным, трудолюбивым, много знать). Мы с вами постараемся, покажем свои знания.
3. -А на чем мы полетим в космос. (на ракете)
Конструирование ракет. Работа с геометрическим материалом. Дано 9 равных треугольников. Построить «ракету».
4. Космонавты перед полётом много тренируются, серьёзно готовятся. Сейчас мы проверим, как наши экипажи готовы к полёту. Слушайте мои задачки:
3 котенка вечерком
Заглянули к кошке в дом –
Свяжи-ка нам носочки
Из шерсти, что в клубочках.
Помогите сосчитать,
Сколько надо ей связать. (3 ·4 = 12)
У каждой мамы-кошки
По 3 маленькие крошки.
Сколько всего котят
Во дворе сидят,
Если кошек 3? (3· 7 = 21)
Змей Горыныч приказал кузнецу
сделать для его дворца 3 замка
и к каждому замку 3 ключа:
медный, серебряный и золотой.
Сколько ключей должен сделать кузнец? (3·3 = 9)
В нашем доме беспорядок,
Не найдешь у нас тетрадок.
В трех шкафах по 6 тетрадок
Мурзик разбросал.
Сколько же всего тетрадок,
Кто бы сосчитал? (3·6 = 18)
Молодцы, старт дан.
5. Внимание! Наш полёт пройдёт по маршруту:
Планета Земля – спутник её Луна — планета Марс – примарсимся, отдохнём; планета Венера, её облетаем и возвращаемся домой на нашу планету Земля. Маршрут полёта изображён на экране.
6. Приземлились на Луну. Взяли ручки. Прописываем цифры.Работа в тетрадях, письмо цифр 3,33,
3х3 … 3х4 3 ×6 3х6 … 3х5…3333х33335
3х7 … 3х2 3х8 …3х10 итог
IV.Физкультминутка.
Долетели мы до Марса,
Примарсились, отдохнём!
Физзарядочку начнём.
Ой, нас что – то укачало!
Закачало, понесло:
То направо, то налево
То назад, а то вперёд!
Закружило, завертело
И на место принесло!
7. Полёт продолжается на планету Марс
От Земли до Марса 55 000 000км.
Встретили нас необычные существа – марсианин.
Кто хочет стать марсианином. Он предложил нам следующие задания: замени сложение умножением (на доске)
3+3+3=
3+3+3+3=
3+2+3+3+3=
3+3+3+3+3+3+3= итог
Примеры в тетрадях.
3х5-9= 3х6+20= итог
3х8+4= 3х9-27=
С заданием справились,
Дальше отправились.
Экипажи готовы?
Ремни пристегнули?
Наш маршрут лежит на планету Венера, но преграждает нам …
8. Млечный путь
Это гигантская туманная спираль из 200 миллиардов звёзд. Нам нужно его преодолеть и решить задачу.
Ваня на уроке труда сделал 12 звездочек и разделила трём девочкам поровну. Сколько звездочек получила каждая девочка? итог
Мы с лёгкостью преодолели препятствие и подлетели к планете Венера.
Это очень горячая планета, температура на ней 470 градусов, мы только поприветствуем её.
8. Возвращаемся на нашу родную планету Земля
V. Итог урока
Дом.задание ст.66 №19 замени умножение сложением
Кто справится с заданием?
Кому задание кажется трудным?
Над какой темой работали?
Какое впечатление у вас осталось от этого урока?
Сегодня хорошо поработали…
Моя планета – человеческий дом,
Но как же жить под данным колпаком?
Где сточная канава – океан?!
Где вся природа поймана в капкан.
Где места нет ни аисту, ни льву.
Где стонут травы: больше не могу!..
Вот она летит , маленькая такая!
Всё ещё живёт !
Всё ещё людям верит!
Вот она плывёт сквозь грозовую полночь.
Всех людей зовёт, просит прийти на помощь.
Просит прийти на помощь.
Просит прийти на помощь.
Давайте, ребята, мы поможем нашей планете. Будем ее беречь!
Умножение и деление целых чисел
При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.
При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Также, необходимо изучить несколько законов умножения и деления. Изучение этих правил позволяет избежать некоторые досадные ошибки в будущем.
Законы умножения
Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов, и разумнее будет изучать их последовательно по мере необходимости.
Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.
Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.
Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.
Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.
Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:
Таким образом, если число 3 повторить два раза подряд, получится число 6.
Переместительный закон умножения
Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:
От перестановки мест сомножителей произведение не меняется.
Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.
3 × 5 = 15
Теперь поменяем местами сомножители:
5 × 3 = 15
В обоих случаях, мы получаем ответ 15, значит между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:
3 × 5 = 5 × 3
15 = 15
А с помощью переменных переместительный закон умножения можно записать так:
a × b = b × a
где a и b — сомножители
Сочетательный закон умножения
Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
К примеру выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:
3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24
Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(3 × 2) × 4 = 3 × (2 × 4)
24 = 24
а с помощью переменных сочетательный закон умножения можно записать так:
a × b × c = (a × b) × c = a × (b × c)
где вместо a, b, c могут стоять любые числа.
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.
Например, найдём значение выражения (2 + 3) × 5
Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25
Значит значение выражения (2 + 3) × 5 равно 25.
С помощью переменных распределительный закон умножения записывается так:
(a + b) × c = a × c + b × c
где вместо a, b, c могут стоять любые числа.
Закон умножения на ноль
Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Например, выражение 0 × 2 равно нулю
0 × 2 = 0
В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Ответ — никак.
Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».
И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:
0 × 2 = 2 × 0
0 = 0
Примеры применения закона умножения на ноль:
5 × 0 = 0
5 × 5 × 5 × 0 = 0
2 × 5 × 0 × 9 × 1 = 0
В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.
Мы рассмотрели основные законы умножения. Далее рассмотрим умножение целых чисел.
Умножение целых чисел
Пример 1. Найти значение выражения −5 × 2
Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Для таких случаев нужно применять следующее правило:
Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.
−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10
Обычно записывают короче: −5 × 2 = −10
Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.
2 × 3 = 6
Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить двойку. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:
То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы
А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.
Пример 2. Найти значение выражения 12 × (−5)
Это умножение чисел с разными знаками. 12 – положительное число, (−5) – отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:
12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60
Обычно решение записывают покороче:
12 × (−5) = −60
Пример 3. Найти значение выражения 10 × (−4) × 2
Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:
Первое действие:
10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40
Второе действие:
−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80
Значит значение выражения 10 × (−4) × 2 равно −80
Запишем решение покороче:
10 × (−4) × 2 = −40 × 2 = −80
Пример 4. Найти значение выражения (−4) × (−2)
Это умножение отрицательных чисел. В таких случаях нужно применять следующее правило:
Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8
Плюс по традиции не записываем, поэтому просто записываем ответ 8.
Запишем решение покороче (−4) × (−2) = 8
Возникает вопрос почему при умножении отрицательных чисел вдруг получается положительное число. Давайте попробуем доказать, что (−4) × (−2) равно 8 и ни чему другому.
Сначала запишем следующее выражение:
4 × (−2)
Заключим его в скобки:
( 4 × (−2) )
Прибавим к этому выражению наше выражение (−4) × (−2). Его тоже заключим в скобки:
( 4 × (−2) ) + ( (−4) × (−2) )
Всё это приравняем к нулю:
(4 × (−2)) + ((−4) × (−2)) = 0
Теперь начинается самое интересное. Суть в том, что мы должны вычислить левую часть этого выражения, и в результате получить 0.
Итак, первое произведение (4 × (−2)) равно −8. Запишем в нашем выражении число −8 вместо произведения (4 × (−2))
−8 + ((−4) × (−2)) = 0
Теперь вместо второго произведения временно поставим многоточие
−8 + … = 0
Теперь внимательно посмотрим на выражение −8 + … = 0. Какое число должно стоять вместо многоточия, чтобы соблюдалось равенство? Ответ напрашивается сам. Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство. Ведь −8 + 8 равно 0.
Возвращаемся к выражению −8 + ((−4) × (−2)) = 0 и вместо произведения ((−4) × (−2)) записываем число 8
−8 + 8 = 0
Пример 5. Найти значение выражения −2 × (6 + 4)
Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)
−2 × (6 + 4) = −2 × 6 + (−2) × 4
Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение
Первое действие:
−2 × 6 = −12
Второе действие:
−2 × 4 = −8
Третье действие:
−12 + (−8) = −20
Значит значение выражения −2 × (6 + 4) равно −20
Запишем решение покороче:
−2 × (6 + 4) = (−12) + (−8) = −20
Пример 6. Найти значение выражения (−2) × (−3) × (−4)
Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
(−2) × (−3) = 6
Второе действие:
6 × (−4) = −(6 × 4) = −24
Значит значение выражения (−2) × (−3) × (−4) равно −24
Запишем решение покороче:
(−2) × (−3) × (−4) = 6 × (−4) = −24
Законы деления
Прежде чем делить целые числа, необходимо изучить два закона деления.
В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.
Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.
Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.
Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.
Далее рассмотрим законы деления.
На ноль делить нельзя
Любое число запрещено делить на ноль.
Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.
Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2
Точно так же можно поступать и с другими выражениями. Если к примеру, 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6
12 : 6 = 2
Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю
5 × 0 = 0
Если записать это выражение в обратном порядке, то получим:
0 : 0 = 5
Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.
В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0
0 : 0 = 2
В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.
Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.
Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8
… × 2 = 8
Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:
8 : 2 = 4
Получили число 4. Запишем его вместо многоточия:
4 × 2 = 8
Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5
… × 0 = 5
Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.
Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.
А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.
С помощью переменных данный закон записывается следующим образом:
, при b ≠ 0
Это выражение можно прочитать так:
Число a можно разделить на число b, при условии, что b не равно нулю.
Свойство частного
Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.
Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3
12 : 4 = 3
Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3
(12 × 4) : (4 × 4)
(12 × 4) : (4 × 4) = 48 : 16 = 3
Получили ответ 3.
Теперь попробуем не умножить, а разделить делимое и делитель на число 4
(12 : 4) : (4 : 4)
(12 : 4) : (4 : 4) = 3 : 1 = 3
Получили ответ 3.
Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.
Мы рассмотрели два закона деления. Далее рассмотрим деление целых чисел.
Деление целых чисел
Пример 1. Найти значение выражения 12 : (−2)
Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.
12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6
Обычно записывают покороче:
12 : (−2) = −6
Пример 2. Найти значение выражения −24 : 6
Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.
−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4
Запишем решение покороче:
−24 : 6 = −4
Пример 3. Найти значение выражения −45 : (−5)
Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.
−45 : (−5) = |−45| : |−5| = 45 : 5 = 9
Запишем решение покороче:
−45 : (−5) = 9
Пример 4. Найти значение выражения −36 : (−4) : (−3)
Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.
Разделим −36 на (−4), и полученное число разделим на −3
Первое действие:
−36 : (−4) = |−36| : |−4| = 36 : 4 = 9
Второе действие:
9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3
Запишем решение покороче:
−36 : (−4) : (−3) = 9 : (−3) = −3
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Внетабличное деление / Деление / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
- Внетабличное деление
Внетабличное деление на однозначное число
99 : 9 = ?
Рассуждай так:
В числе 99 – 9 десятков и 9 единиц; делю 9 десятков на 9, получаю 1 десяток, или это число 10; далее делю 9 единиц на 9 и получаю число 1. Теперь к 10 прибавляю 1 и получаю 11. Тогда,
99 : 9 = 11

84 : 4 = ?
Рассуждай так:
В числе 84 – 8 десятков и 4 единицы; делю 8 десятков на 4, получаю 2 десятка, или это число 20; далее делю 4 единицы на 4 и получаю число 1. Теперь к 20 прибавляю 1 и получаю 21. Тогда,
84 : 4 = 11
Нахождение частного подбором
87 : 29 = ?
Пробуем в частном 2 и проверяем: 29 • 2 = 58, 58 < 87, число 2 не подходит.
Пробуем в частном 3 и проверяем: 29 • 3 = 87, 87 = 87, значит, 87 : 29 = 3.
Внетабличное деление на двузначное число
Если ты еще не умеешь решать такие примеры столбиком, то можно решать при помощи умножения.
Рассуждай так:
Деление суммы на число
Чтобы разделить сумму на число, можно вычислить сумму и разделить её на число или разделить на число каждое слагаемое и полученные результаты сложить.
Случай 1:
(15 + 25) : 5 = ?
Рассуждай так:
Способ 1:
Нахожу сумму чисел 15 и 25, получаю 40. Теперь 40 делю на 5 и получаю 8.
Записываю так:
(15 + 25) : 5 = 40 : 5 = 8
Способ 2:
Каждое из слагаемых делю на 5 и результат складываю. Сначала делю первое слагаемое 15 на 5, получу 3, потом на 5 разделю второе слагаемое 25, получу 5, теперь полученные результаты 3 и 5 сложу и получу 8. Запишу так:
(15 + 25) : 5 = 15 : 5 + 25 : 5 = 3 + 5 = 8
Значит, (15 + 25) : 5 = 8
Случай 2:
36 : 2 = ?
Рассуждай так:
Число 36 представлю в виде суммы слагаемых, которые легко делятся на 2, например, 20 и 16. Эту сумму надо разделить на 2.
32 : 2 = (20 + 16) : 2 = ?
Сначала делю первое слагаемое 20 на 2, получу 10, потом на 2 разделю второе слагаемое 16, получу 8, теперь полученные результаты 10 и 8 сложу и получу 18.
32 : 2 = (20 + 16) : 2 = 20 : 2 + 16 : 2 = 10 + 8 = 18
Значит, 36 : 2 = 18
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное деление
Деление с остатком
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Деление
Правило встречается в следующих упражнениях:
3 класс
Страница 14,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 25,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 71,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 61,
Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 62,
Моро, Волкова, Рабочая тетрадь, 2 часть
4 класс
Страница 7,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 13,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 25,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 52,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 88,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 8,
Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 36,
Моро, Волкова, Рабочая тетрадь, 1 часть
5 класс
Упражнение 241,
Мерзляк, Полонский, Якир, Учебник
Упражнение 242,
Мерзляк, Полонский, Якир, Учебник
Упражнение 254,
Мерзляк, Полонский, Якир, Учебник
Упражнение 264,
Мерзляк, Полонский, Якир, Учебник
Упражнение 291,
Мерзляк, Полонский, Якир, Учебник
Упражнение 5,
Мерзляк, Полонский, Якир, Учебник
Упражнение 316,
Мерзляк, Полонский, Якир, Учебник
Упражнение 317,
Мерзляк, Полонский, Якир, Учебник
Упражнение 318,
Мерзляк, Полонский, Якир, Учебник
Упражнение 365,
Мерзляк, Полонский, Якир, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
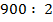 б)
б) 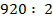
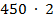 г)
г) 
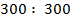 в)
в) 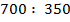
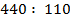 г)
г)