Деление столбиком — Википедия
Материал из Википедии — свободной энциклопедии
 Процесс деления столбиком (американо-британский вариант) числа 1 260 257 на число 37
Процесс деления столбиком (американо-британский вариант) числа 1 260 257 на число 37
Деление столбиком (также известное как деление уголком) — стандартная процедура в арифметике, предназначенная для деления простых или сложных многозначных чисел за счёт разбивания деления на ряд более простых шагов. Как и во всех задачах на деление, одно число, называемое делимым, делится на другое, называемое делителем, производя результат, называемый частным. Этот способ позволяет выполнять деление произвольно больших чисел, разбивая процесс на серию последовательных простых шагов.[1]
В Европу этот метод деления попал от арабов и получил названия «золотого деления» (по сравнению с гораздо более сложным «железным делением» на абаке, применявшимся ранее). Он долгое время конкурировал с делением «методом галеры», который выгодно отличается отсутствием умножения на многозначные числа[2].
Обозначение в Бельгии, Испании, Франции, Монголии и на постсоветском пространстве[править | править код]
На постсоветском пространстве делитель располагается справа от делимого, отделяемого от него вертикальной чертой. Деление также происходит в столбик, но частное (результат) записывается ниже делителя и отделяется от него горизонтальной чертой.
8420│4 500│4
-8 │2105 -4 │125
4 10
- 4 - 8
20 20
- 20 -20
0 0
- В некоторых странах Европы применяется другое обозначение. Вычисление абсолютно такое же, но записывается иначе, как показано на примере:
959 ÷ 7 => 137 (Пояснение)
7 (7 × 1 = 7)
25 (9 - 7 = 2)
21 (7 × 3 = 21)
49 (25 - 21 = 4)
49 (7 × 7 = 49)
0 (49 - 49 = 0)
и
127 ÷ 4 = 31.75 (12 - 12 = 0 который записан на следующей линии)
07 (семь переносится из делимого 127)
4
3.0 (3 - это остаток, который разделён на 4 для получения 0.75)
2 8 (7 × 4 = 28)
20 (дополнительный ноль переносится)
20 (5 × 4 = 20)
0
Вычисление абсолютно такое же, но записывается иначе (делитель располагается слева от делимого), как показано на примере деления 135 на 11 (с результатом 12 и остатком 3):
11 / 135 \ 12
11
--
25
22
--
3
| Символ деления столбиком | |
|---|---|
| ⟌ | |
Изображение
| |
| long division | |
| Юникод | U+27CC |
| HTML-код | |
| UTF-16 | 0x27CC |
| %E2%9F%8C | |
При делении на бумаге не используются символы косой черты (/) или обелюса (÷). Вместо этого делимое, делитель и частное (в процессе нахождения) располагаются в таблице. Пример деления 500 на 4 (с результатом 125):
125 (Пояснение)
4|500
4 (4 × 1 = 4)
10 (5 − 4 = 1)
8 (4 × 2 = 8)
20 (10 − 8 = 2)
20 (4 × 5 = 20)
0 (20 − 20 = 0)
Пример деления с остатком:
31.75
4|127
12 (12 − 12 = 0, который записан на следующей линии)
07 (семь переносится из делимого 127)
4
3.0 (3 — это остаток, который разделён на 4 для получения 0.75)
2 8 (7 × 4 = 28)
20 (дополнительный ноль переносится)
20 (5 × 4 = 20)
0
- Во-первых, обратите внимание на делимое (127), чтобы определить может ли делитель (4) вычитаться из него (в нашем случае не может, так как мы имеем единицу как первую цифру и мы не можем использовать отрицательные числа, поэтому нельзя написать −3)
- Если первая цифра недостаточно велика, мы берём вместе с ней следующую цифру. Таким образом в нашем распоряжении как первое число теперь будет число 12.
- Возьмите максимальное число четвёрок, которое может быть вычтено из первого числа. В нашем случае из 12 может быть вычтено 3 четвёрки
- В частном (над второй цифрой делимого, так как это последняя цифра которая используется) напишите получившуюся тройку, а под делимым число 12
- Вычтите 12, которую вы написали, из соответствующего числа выше него (результат будет, конечно, 0)
- Повторите первый шаг
- Так как 0 — неподходящее число для делимого, перенесите следующую цифру из делимого (7). В результате получится 07
- Повторите шаги 3, 4 и 7
- У вас будет число 31 в частном, 3 в качестве остатка и больше ни одного числа в делимом
- Можно продолжить деление, получая в частном десятичную дробь: добавьте к частному справа точку, а к остатку (3) справа ноль и продолжайте деление, добавляя ноль всякий раз, когда делимое меньше делителя (4)
Как делить в столбик — Компьютер для новичков
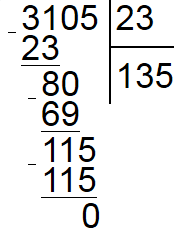
В настоящее время современные технологии развиваются стремительными темпами, и все больше работы за нас выполняют компьютеры и различные другие электронные устройства. Тем не менее, умение выполнять арифметические операции без помощи калькулятора остаются все еще востребованными.
Ранее мы уже рассматривали, как складывать, вычитать и умножать в столбик на листе бумаги. Поэтому сегодня давайте освежим в памяти, а возможно кто-то узнает впервые алгоритм деления столбиком без калькулятора. В этом нет ничего сложного, главное внимательность и аккуратность.
Для начала запомним, что число которое делится называется делимое. Число на которое делят называют делителем, а результат деления частным. Чтобы было проще, давайте рассмотрим деление в столбик на конкретном примере и разделим 834 на 6. Первое что нам необходимо сделать, это записать их соответствующим образом.
Пишем делимое, затем правее него делитель и отделяем их друг от друга так называемым уголком. Все подготовительные операции выполнены и переходим непосредственно к делению в столбик.
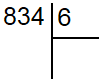
Для этого необходимо в делимом двигаясь слева на право найти наименьшее число большее или равное делителю. Делитель у нас равен 6, а первая цифра в делителе равна 8 и она больше 6. Теперь необходимо найти сколько целых раз делитель помещается в неполном делимом, в данном случае всего один раз. Поэтому под делителем пишем 1, а под 8 записываем 6 проводим горизонтальную черту и находим их разность по правилам вычитания столбиком, то есть 2. Поскольку 2 меньше нашего делителя (6), то все сделано правильно, в противном случае, где то допущена ошибка.
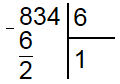
Теперь сносим вниз следующую цифру исходного делимого (3) и проверяем чтобы получившееся число (23) было больше делителя (6). В данном случае это так. Снова находим сколько раз делитель помещается в неполном делимом, получается 3 раза. Поэтому под делителем записываем 3, а под делимым находим разность 23 и 18 (6*3), которая равна 5.
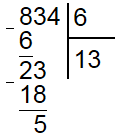
Дальше делаем все точно также, сносим вниз следующее число из делимого (4), получается число 54 и находим сколько раз в нем умещается делитель (6). Он умещается 9 раз, значит под делителем записываем 9, а под неполным делимым 54 (6*9). Поскольку 54 отнять 54 равно нулю и в делимом не осталось больше чисел, то деление закончено и частное равно 139. Можете проверить на калькуляторе или выполнив умножение в столбик 6 на 139.
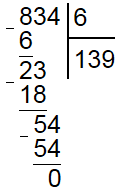
Чтобы закрепить навык деления столбиком давайте рассмотрим еще один пример и разделим 1587 на 23. Согласно уже известному нам алгоритму находим в делимом наименьшее число большее или равное делителю, таким числом является 158. Делитель 23 умещается в неполном делимом 6 раз. Соответственно под делителем пишем 6, а под делимым 138 (23*6) и находим разность 158 и 138.
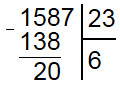
Поскольку 20 меньше делителя все сделано правильно, теперь сносим вниз следующее число (7) и находим сколько раз умещается делитель в получившемся числе 207. Он умещается 9 раз, а поскольку 207-207=0 и в делимом больше нет чисел, то деление в столбик законченно и ответ равен 69.
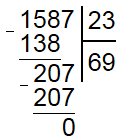
Как видите, ничего особо сложного нет, главное внимательность. Хотя внимательный читатель наверняка уже обратил внимание, что в обоих приведенных примерах делитель помещается в делимом целое число раз. Однако так бывает далеко не всегда, поэтому рассмотрим пример деления столбиком с остатком, для этого разделим 46 на 8.
Поскольку 4 меньше 8, то наименьшим неполным делимым является 46. В числе 46 делитель содержится 5 раз, следовательно под делителем пишем 5, а под делимым 40 (5*8).
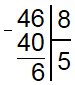
Разность 46 и 40 равна 6. Число 6 меньше делителя, значит мы все сделали верно, но в делимом больше не осталось чисел, а разность не равна 0. Это значит, что разделить эти два числа без остатка нельзя. Чтобы найти остаток поступаем следующим образом. В разности ставим запятую, а к остатку приписываем 0. В остатке имеем число 60. Делитель умещается в нем 7 раз, значит пишем в разность 7 и вычитаем из 60 число 56 (8*7).
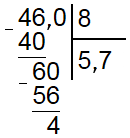
В остатке имеем 4, снова приписываем 0. Получается 40 и делитель умещается в нем 5 раз. В частное записываем 5 и вычитаем из остатка 40, получается 0.
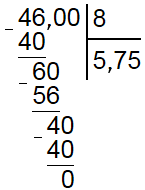
Таким образом, мы разделили 46 на 8 столбиком и получили ответ 5,75. Теперь вы знаете, как делить в столбик без калькулятора. Кстати в Windows есть встроенный калькулятор «Пуск» ⇒ «Стандартные» ⇒ «Калькулятор», в котором всегда можно быстро выполнить необходимые вычисления.
как объяснить ребенку деление в столбик :: SYL.ru
Деление в столбик – это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик – это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое – это число, которое будет делиться на равные части, делитель – указывать, на сколько частей нужно разделить число, частное – это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа – меньшее.
- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.

- Записывают в столбик 2 числа: делимое – 536 и делитель – 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 – 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
- К единице сносится следующее разрядное число – 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 – в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число – 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления – 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Деление в столбик, правила и подробное описание алгоритма решения, деление десятичных дробей, примеры деления в столбик с остатком, как научить ребенка делить столбиком
Повторяем термины
Если вы уже немного знакомы с арифметическими действиями, то, наверное, знаете, как называются числа, с которыми придется иметь дело:
- делимое — это то, что вам нужно разделить;
- делитель — на него всегда делят;
- частное — то, что получается в итоге.
В Интернете есть немало сайтов, где это действие можно выполнить с помощью онлайн-калькулятора.
Важно! Если вы хотите объяснить принцип деления ребенку, не забудьте проверить, помнит ли он правила умножения.
Без умения перемножать числа в этом случае никак не обойтись, ведь результат всегда нужно проверить, а сделать это можно только обратным действием, то есть умножением. Конечно, навыки сложения и вычитания при освоении деления тоже не повредят.
Как записать?
Даже ученик начальных классов знает, как записываются примеры. Между делимым и делителем ставится двоеточие, после примера — знак равенства, а в конце пишется результат. Но простенькие задания с однозначными числами занимают всего одну строчку, а как быть в случае со столбиком, ведь придется делить двузначные, трехзначные и даже еще более крупные числа? Да точно так же, двоеточие вполне годится. Но есть и второй способ — вот такой значок
I_
Такой способ записи называется “уголком”. Слева от вертикальной линии пишется число, которое мы будем делить, над горизонтальной черточкой — делитель, а под ней — частное. Обычный тетрадный лист подходит для такой записи больше, но при желании все возможно и в ворде
Деление с остатком и без
Иметь дело мы будем с целыми числами, а вот в результате может получиться и десятичная дробь, в зависимости от того, допустимо ли в задании частное с остатком. Для начала попробуем разделить трехзначное число на однозначное.
Пример 1
Возьмем 216 разделить 3. Попробуем записать пример:
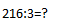
Посмотрим, какая из первых цифр делится нацело на 3. Двойка? Нет. Значит, берем две цифры — 21. Получится 7, а промежуточное действие будет выглядеть так: 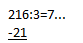 Теперь остается разделить на 3 последнюю цифру — 6, потому после первого шага остаток не образовался. Шестерку в столбике надо написать строго под той, что стоит в примере — в этом главный фокус, иначе можно очень легко сбиться. Что ж, давайте запишем аккуратно. Например, вот так:
Теперь остается разделить на 3 последнюю цифру — 6, потому после первого шага остаток не образовался. Шестерку в столбике надо написать строго под той, что стоит в примере — в этом главный фокус, иначе можно очень легко сбиться. Что ж, давайте запишем аккуратно. Например, вот так: 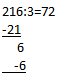
Пример 2
Но может быть и другая ситуация. Например, когда первые две цифры на однозначное число нацело не делятся. Ничего страшного. Записываем:
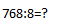
Первым делом придется делить 76, никуда не денешься. Ближайшее число, кратное 8 (то есть то, которое делится без остатка), — 72. Его и будем отнимать. Получим 9, которое сразу запишем в частное, и 4 в остатке — его нужно поместить под чертой: 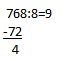
Следующий шаг — дописать к этой четверке последнюю цифру. Получится 48, его мы на 8 и разделим, от этого действия получится вторая цифра в результате — 6. Наш пример будет выглядеть теперь вот так: 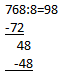
Двузначный делитель
Что будет, если попробовать выполнить другую операцию — разделить то же самое число 768 не на 8, а, скажем, на 16? Да то же самое. Возьмем первые две цифры, посмотрим, какое ближайшее число кратно 16 — это 64. Отнимаем его от 72, получаем 8. К восьмерке приписываем цифру делимого, которую мы еще не задействовали, то есть 8. Пример принимает следующий вид: 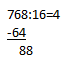 Да, но 88 на 16 тоже не делится! Во всяком случае, без остатка. Что ж, тогда поступаем так:
Да, но 88 на 16 тоже не делится! Во всяком случае, без остатка. Что ж, тогда поступаем так: 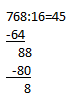 Можно, конечно, больше ничего не делать и записать ответ как 45 (остаток 8). Но есть и другие варианты решения. Если бы число было четырехзначным — все оказалось бы куда проще! А почему бы и не превратить его в четырехзначное? Представим, что делимое у нас записано иначе — 768,0. Тогда мы можем после пятерки тоже поставить запятую и превратить целое число в десятичную дробь. В данном случае она конечна, но бывают примеры и с бесконечными дробями. Вот что получается:
Можно, конечно, больше ничего не делать и записать ответ как 45 (остаток 8). Но есть и другие варианты решения. Если бы число было четырехзначным — все оказалось бы куда проще! А почему бы и не превратить его в четырехзначное? Представим, что делимое у нас записано иначе — 768,0. Тогда мы можем после пятерки тоже поставить запятую и превратить целое число в десятичную дробь. В данном случае она конечна, но бывают примеры и с бесконечными дробями. Вот что получается: 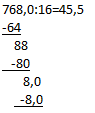
Деление меньшего числа на большее
А можно ли в столбик разделить меньшее число на большее? Ничто не помешает это сделать. Вообще-то арифметика — это веселая и увлекательная игра со своими правилами. Главное — учимся соблюдать порядок. Итак, пробуем быстро разделить 36 на 540. Записываем выражение так:  Поскольку первое число меньше второго, то и результат будет меньше единицы, то придется иметь дело с нулями. Объяснение простое: частное показывает, сколько раз делитель укладывается в делимое. Если нисколько — значит, результат начинается с нуля:
Поскольку первое число меньше второго, то и результат будет меньше единицы, то придется иметь дело с нулями. Объяснение простое: частное показывает, сколько раз делитель укладывается в делимое. Если нисколько — значит, результат начинается с нуля: 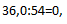 А дальше действуем, как в предыдущих примерах:
А дальше действуем, как в предыдущих примерах: 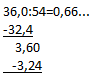 Числа в столбике начинают повторяться, то есть получается бесконечная десятичная дробь.
Числа в столбике начинают повторяться, то есть получается бесконечная десятичная дробь.
Как проверить результат деления?
Результат, как и всегда, проверяется умножением. Если остатка не было, просто перемножаем частное и делитель любым удобным способом — кстати, умножать в столбик тоже удобно. Если делить нацело не получилось, опять же, перемножаем частное и делитель, а затем прибавляем остаток.
Важно! Если результатом получилась бесконечная десятичная дробь, проверка может быть лишь приблизительной — в результате умножения у вас должно получиться число, очень близкое к делимому.
Эти навыки очень помогут потом, когда придется считать не числа, обозначенные цифрами, а действовать в мире одночленов и многочленов. Ведь полиномы — это тоже числа, только выраженные иначе. Еще больше наглядных примеров деления в столбик смотрите в предложенном ниже видео.
Как делить в уме 🚩 как быстро делить числа 🚩 Математика
Инструкция
Несколько десятилетий назад в обычных образовательных школах существовал предмет «Устный счет». Дети обучались производить в уме основные математические операции: сложение, вычитание, умножение и деление, которое можно считать самым сложным из них. Деление предполагает быстрый поиск максимального делителя. Метод устного деления требует знания приемов сокращенного деления и школьной таблицы умножения. Кроме того, нужно тренировать память, чтобы научиться держать в уме все промежуточные вычисления, особенно если цифры большие.
Разложение частного на составляющиеНапример, вам нужно разделить число 3647 на 7. Представьте частное как сумму чисел 3500 и 147. В этом примере 3500 – самое большое очевидное число, меньшего исходного, которое делится на 7 без остатка:3647/7 = 3500/7 + 147/7 = 500 + 147/7 = 500 + 21 = 521.
Деление «столбиком» в уме, как в детствеМысленно представьте лист бумаги и воображаемым карандашом произведите вычисления. Этот метод требует хорошей зрительной памяти, которую, впрочем, можно натренировать регулярными упражнениями в счете. Этот метод предпочитают многие, т.к. он хорошо знаком со школьных времен, хоть и не такой быстрый, как предыдущий.
Деление на 10, 100, 1000 и т.д.Этот способ предполагает отделение соответствующего числа запятых, начиная с правой стороны числа. Например, разделите число 567890 на 10000:567890/10000 = 56,7890 – отделение четырех нулей.
Деление на 0,1, 0,01 и т.д.Этот вариант предполагают умножение на 1 с соответствующим числом последующих нулей, т.е. десятичную дробь переворачивают. Например, разделите число 78,765 на 0,0001:78,765/0,0001 = 78,765*10000 = 787650.
Деление на десятичную дробьЗамените ее мысленно на обычную, например, 0,5 на 1/2. Умножьте исходное число на знаменатель и разделите на числитель. Например, разделите число 2250 на 0,75:2250/0,75 = 2250/(3/4) = 2250*4/3 = 9000/3 = 3000.
Деление на 5, 50, 500 и т.д.Замените делитель на соответствующую дробь: 5 = 10/2; 50 = 100/2 и т.д. Теперь достаточно отделить у частного два знака после запятой и умножить на 2. Например, разделите 1750 на 50:1750/50 = 1750*2/100 = 3500/100 = 35.
По схожему принципу происходит деление на 2,5, 25 и пр.: делитель заменяется на соответствующую дробь с 4 в знаменателе. 1,25, 12,5 и пр. – на дробь с 8 в знаменателе:285/2,5 = 285*4/10 = 1140/10 = 114;600/12,5 = 600*8/100 = 4800/100 = 48.
Как научиться делить в столбик 🚩 как делить числа столбиком 🚩 Математика
Вам понадобится
- — ручка или карандаш,
- — лист бумаги в клетку.
Инструкция
Деление без остатка. Разделим 1265 на 55.
Проведите вниз короткую вертикальную линию, высотой в несколько клеток. От этой линии проведите перпендикуляр вправо. Получилась буква «Т», заваленная на левый бок. Над горизонтальной частью заваленной буквы «Т» пишется делитель (55), а слева от него в этой же строчке, за вертикальной частью буквы «Т» – делимое (1265). Обычно, сначала записывается делимое, потом ставится знак деления в столбик (заваленная набок буква «Т»), а после делитель.
Определите, какая часть делимого (отсчет идет слева направо по старшинству разрядов) делится на делитель. То есть: 1 на 55 – нет, 12 на 55 – нет, 126 на 55 – да. Число 126 называется неполным делимым.
Прикиньте в уме, на какое число N нужно умножить делитель, чтобы получилось число равное или максимально приближенное (но не большее) к величине неполного делимого. То есть: 1*55 – маловато, 3*55=165 – многовато. Итак, наш выбор – число 2. Записываем его под делителем (ниже горизонтальной части заваленной буквы «Т»).
Умножьте 2 на 55 и запишите полученное число 110 строго под цифрами неполного делимого – слева направо: 1 под 1, 1 под 2 и 0 под 6. Сверху 126, снизу 110. Проведите под 110 короткую горизонтальную черту.
Вычтите из 126 число 110. Получится 16. Цифры записывайте четко одна под другой под проведенной чертой. То есть, слева направо: под цифрой 1 числа 110 – пусто, под цифрой 1 – 1 и под цифрой 0 – 6. Число 16 – это остаток, который должен быть меньше делителя. Если он оказался больше делителя, число N было выбрано неправильно – нужно его увеличить и повторить предыдущие действия.
Снесите следующую цифру делимого (цифра 5) и запишите ее справа от числа 16. Получилось 165.
Повторите действия третьего шага для отношения 165 к 55, то есть найдите число Q, при умножении делителя на которое, получается число максимально приближенное к 165 (но не большее его). Это число 3 – 165 делится на 55 без остатка. Запишите цифру 3 справа от цифры 2 под чертой, проведенной под делителем. Это и есть ответ: частное отношения 1265 к 55 равно 23.
Деление с остатком. Разделим 1276 на 55.Повторите все те же действия, что и при делении без остатка. Число N по-прежнему равно 2, но разница между 127 и 110 равна 17. Сносим 6 и определяем число Q. Оно также по-прежнему равно 3, но теперь появляется остаток: 176 – 165 = 11. Остаток 11 меньше 55, вроде бы все нормально. Но сносить-то больше нечего…
Допишите справа от делимого ноль и поставьте запятую, после цифры 3 в частном (то число, которое получается в ходе деления, и записывается под чертой, проведенной под делителем).
Снесите дописанный в делимом ноль (запишите его справа от 11) и проверьте, есть ли возможность разделить получившееся число на делитель. Ответ – да: 2 (обозначим его, как число G) умножить на 55 равно 110. Ответ — 23,2.Если бы снесенного в предыдущем шаге нуля не хватило бы для того, чтобы остаток с дописанным нулем оказался больше делителя, нужно было бы дописать еще один ноль в делимом и поставить 0 в частном после запятой (получилось бы 23,0…).
Деление в столбик десятичных дробей.Перенесите запятую на одинаковое количество знаков вправо в делимом и делителе так, чтобы и там, и там были целые числа. Дальше – алгоритм деления тот же.
