Нестандартные задачи по математике для 4-5 классов
Для успешного овладения любым предметом необходима творческая работа. И математика не исключение. Вернее, к математике это относится в первую очередь.
Только творчески проанализировав условие можно найти наиболее простой путь решения задачи, а, зачастую, решить ее вообще. Именно такие задачи принято называть нестандартными. Цель данной статьи – помочь читателю обогатить свой опыт в решении нестандартных задач.
Задача 1.
У бабушки есть гуси и кролики. У них вместе 25 голов и 58 лапок. Сколько гусей и сколько кроликов у бабушки?
Решение.
1 способ.
Если бы у бабушки были только гуси. Тогда общее количество лапок составляло 2 · 25 = 50. Не хватило бы ещё 58 – 50 = 8 лапок. Если гуся заменить кроликом, то количество лапок увеличится на 2. Нам надо количество лапок увеличить на 8. Следовательно, надо 8 : 2 = 4 гуся заменить на 4 кролика. Значит у бабушки 21 гусь и 4 кролика. Эти рассуждения можно записать в виде таблицы.
| Количество гусей | Количество кроликов | Количество лапок у всех гусей | Количество лапок у всех кроликов | Общее количество лапок |
| 25 | 0 | 50 | 0 | 50 |
| 24 | 1 | 48 | 4 | 52 |
| 23 | 2 | 46 | 8 | 54 |
| 22 | 3 | 44 | 12 | 56 |
| 21 | 4 | 42 | 16 | 58 |
Из таблицы видно, что условию задачи соответствует последний ряд.
2 способ.
Можно решить задачу с помощью уравнения.
Пусть у бабушки х гусей. Тогда кроликов 25 – х. Количество лапок у гусей 2х, а у кроликов – 4 · (25 – х). Так как по условию задачи общее количество лапок 58, то составим уравнение
2х + 4 · (25 – х) = 58,
2х + 100 – 4х = 58.
100 – 2х = 58,
Х = 21.
Тогда 25 – х = 25 – 21 = 4.
Ответ: 21 гусь, 4 кролика.
Задача 2.
В кругах поместили числа от 11 до 16 так, чтобы сумма чисел на всех сторонах треугольника была одинаковой.
Решение:
Задачу можно решить методом перебора возможных вариантов. Оптимизировать перебор помогут следующие рассуждения:
Сумма всех чисел от 11 до 16 равна 81. Каждому числу найдется место в кружочке. Если сумму всех чисел, поставленных в вершинах, обозначить через Х, а сумму оставшихся трех через У, то, исходя из условия, сумма 2Х + У должна делиться на 3. Или 2Х + У = 3k. Но Х + У = 81. Теперь очевидно, что и Х, и У должны быть кратны 3.
Среди чисел от 11 до 16 два числа делятся на 3, два дают остаток 1 при делении на 3 и два дают в остатке 2. Поэтому план решения выглядит следующим образом:
Разбиваем наши числа на 2 группы по 3 числа в каждой: с остатком 0, с остатком 1 и с остатком 2. (Не всякий вариант здесь является удачным.) Числа одной из групп расставляем по вершинам треугольника, а числа второй – внутри сторон. Естественно, при расстановке чисел второй группы им нужно подобрать «удачные» места. Задача имеет два решения (см. рисунок).

Задача 3.
Какие три цифры можно дописать к числу 19 981 999, чтобы полученное число делилось без остатка на 7, 8, и на 9?
Решение:
Пусть искомое число имеет вид 19 981 999 ***.
Заменим его суммой чисел 19 981 999 *** = 19 981 999 000 + ***.
- Первое слагаемое при делении на 7 даёт остаток 5. Значит, чтобы сумма делилась нацело на 7, надо, чтобы слагаемое *** давало остаток 2. (5 + 2 = 7).
- Первое слагаемое при делении на 9 даёт остаток 1. (Используем признак делимости на 9.
1 + 9 + 9 + 8 + 1 + 9 + 9 + 9 + 0 + 0 + 0 = 55. 55 : 9 = 6 (остаток 1)). Значит, чтобы сумма делилась нацело на 9 надо, чтобы слагаемое *** давало остаток 8. (1 + 8 = 9). - Первое слагаемое целиком делится на 8 (Три последние цифры составляют число, делящееся на 8.) Следовательно, *** должно делиться на 8.
Способом подбора найдём число ***, удовлетворяющее этим трём условиям. Это число 800.
Ответ: 8, 0, 0.
Задача 4.
У продавца было 6 ящиков с вишнями массой 15 кг, 16 кг, 18 кг, 19 кг, 20 кг, 31 кг. Два покупателя взяли 5 ящиков, причём один взял вдвое больше другого. Какой ящик остался?
Решение:
Найдём общее количество вишен.
15 + 16 + 18 + 19 + 20 + 31 = 119 (кг). При делении на 3 это число даёт остаток 2.
Так как по условию задачи первый покупатель взял вдвое больше другого, то масса общего количества вишен, которые купили, кратна 3. Следовательно, должен остаться ящик, масса вишен в котором при делении на 3 даёт остаток 2. Этому условию соответствует ящик массой в 20 кг.
Ответ: 20 кг.
Задача 5.
9 одинаковых конструкторов содержат меньше 100 деталей, а 12 таких же конструкторов больше 130 деталей. Сколько деталей в одном конструкторе?
Решение:
Пусть, a деталей в одном конструкторе.
1) Так как 9 одинаковых конструкторов содержат меньше 100 деталей, то 9 · а < 100. а ≤ 11 (а – натуральное число).
2) В 12 таких же конструкторов больше 130 деталей. Тогда 12 · а > 130 и а > 10.
Условиям 1 и 2 соответствует число 11.
Ответ: 11 деталей.
Задача 6.
Найдите все четырёхзначные числа, у которых каждая цифра больше суммы из более высоких разрядов.
Решение:
Для решения данной задачи используем метод перебора.
Пусть abcd искомое четырёхзначное число, где a, b, c, d – его цифры.
Тогда согласно условию задачи d > a + b + c, c > a + b, b > a. Значение цифры а самое маленькое. Значение 0 она принимать не может, так как по условию задачи число четырёхзначное.
1) Если а = 1, то b > a и b = 2. c > a + b = 1 + 2 = 3. Пусть c = 4. d > a + b + c = 1 + 2 + 4 = 7,
d = 8, либо 9. Наши числа 1248, 1249.
2) Если а = 1, то b > a и b = 2. c > a + b = 1 + 2 = 3. Пусть c = 5. d > a + b + c = 1 + 2 + 5 = 8,
d = 9. Наше число 1259.
c = 6 быть не может, так как тогда d > a + b + c = 1 + 2 + 6 = 9.
3) Если а = 2, то b > a и b = 3. c > a + b = 2 + 3 = 5. Пусть c = 6. d > a + b + c = 2 + 3 + 6 = 11.
А это невозможно.
Ответ: 1248, 1249, 1259.
Задача 7.
Как 9 деревьев посадить в 10 рядах, что бы в каждом из них было по 3 дерева?
Решение:
Решение этой задачи для 8 рядов достаточно простое. (Попробуйте сами). А вот увидеть решение для 10 рядов получается не у каждого.
Чтобы таким образом посадить деревья надо, чтобы каждое дерево относилось к 3 рядам, а одно дерево было задействовано в 4 рядах. Деревья можно разместить следующим образом.

Задача 8.
Незнайка утверждал, что он нашёл такое натуральное число, произведение цифр которого равно 4368. Прав ли он?
Решение:
Число 4368 = 24 · 3 · 7 · 13. Число 13 не может являться цифрой.
Ответ. Следовательно, Незнайка не прав.
Задача 9.
Турист плыл в лодке против течения реки. Проплывая мимо моста, он уронил в воду флягу. Через 10 минут он заметил потерю и поплыл назад. Гребя с тем же усилием, турист догнал флягу в километре от моста. Определить скорость течения реки.
Решение:
Пусть х м/мин собственная скорость лодки, у м/мин скорость течения. Докажем, что скорость изменения расстояния между лодкой и флягой величина постоянная, независящая, от того плывут фляга и лодка в одном направлении или в разных. Скорость фляги совпадает со скоростью течения. Она равна у м/мин. Когда лодка удаляется от фляги, то она плывёт против течения и её скорость (х – у) м/мин. А скорость изменения расстояния равна ((х – у) + у = х) м/мин. Когда лодка догоняет флягу, она плывёт со скоростью (х + у) м/мин. Скорость изменения расстояния равна ((х + у) – у = х) м/мин.
За 10 минут расстояние между лодкой и флягой составляло (10х) м. Значит, чтобы догнать флягу туристу необходимо потратить 10 минут. И так, фляга плыла (10 + 10 = 20) минут. За это время она проплыла 1 км = 1000 м. Скорость фляги – (1000 : 20 = 50) м/мин = 3 км/ч.
Скорость течения равна скорости фляги и равна 3 км/ч.
Ответ: 3 км/ч.
Задача 10.
Бабушка продавала на рынке яйца двум покупателем: первый купил 1/2 всех имевшихся у неё яиц и ещё 15 штук, второй 3/5 остатка и последние 10 штук. Сколько яиц продала бабушка?
Решение:
Эта задача относится к задачам, которые решаются с конца. Следовательно, начинать её решение надо с анализа второй части условия:
1) Второй покупатель получил 3/5 остатка и последние 10 яиц.
10 яиц составляют 2/5 остатка. Тогда остаток – 10 : 2 · 5 = 25 (яиц).
2) Первый покупатель купил 1/2 всех имевшихся яиц и ещё 15 штук. После этого осталось 25 яиц. Отсюда половина яиц составляет (15 + 25 = 40) яиц. Тогда общее количество яиц – 40 · 2 = 80.
Ответ: 80 яиц.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Математика 5 класс
Интерактивный учебник. Математика 5 класс. Описание
Наш интерактивный учебник «Математика 5 класс» рассчитан на повторение, закрепление и проверку ваших знаний по школьному курсу математики в пятом классе. Это отличная тренировка навыков решения задач и примеров. Особенностью учебника является интерактивная проверка ответов на задачи и задания, что позволяет исключить ошибки в ответах, а также возможность подсмотреть ответ.
Все мы порой сталкиваемся с опечатками и ошибками в учебной литературе, что порой весьма огорчает. Мы прикладываем все свои силы и знания, что бы исключить ошибки на наших страницах. В нашем учебнике заложена программная защита от собственных ошибок, которая гарантирует правильную проверку ваших ответов. И все же, если вы заметили опечатку или ошибку, мы будем вам очень признательны за сообщение о ней, которое вы можете отправить, заполнив форму на странице «Контакты».
Пользоваться «Математикой 5 класс» просто. На этой странице в «Оглавлении» находятся ссылки на тематические страницы учебника, где вы можете, нажав на красную ссылку прочитать правила по теме. Ниже расположены задачи и задания, первое из которых открыто по умолчанию, а следующие вы можете открыть, кликнув по их заголовкам мышью. Под заданиями находятся ссылки на соседние темы учебника, что позволяет переходить от темы к теме, не заходя на страницу «Математика 5 класс».
Еще мы хотим развеять ваши сомнения по поводу нагрузки на глаза ребенка, во время занятий на нашем сайте. Основное время ребенок смотрит в тетрадку, которую обязательно надо иметь под рукой для решения задач, а шрифт заданий подобран таким образом, чтобы он легко читался. И все же мы рекомендуем пользоваться кнопками Ctrl+ и Ctrl- для увеличения (уменьшения) размера шрифта.
Несколько важных рекомендаций: Во время решения задач делайте все расчеты на бумаге в столбик, прочерчивайте графические задачи карандашом. В пятом классе это очень важно. Тренируйте устный счет. Ну, вот, пожалуй, и все. Успехов вам на нелегком, но интересном учебном фронте, в том числе и на страницах нашего проекта «Математика 5 класс».
5 класс | Образовательные тесты

Тест по теме — «Начальные сведения о натуральных числах»
Математика 5 класс | Автор: Самарин Дмитрий Сергеевич | ID: 11982 | Дата: 24.2.2020

решение уравнений
Математика 5 класс | Автор: Карадина Евгения Артемовна | ID: 11837 | Дата: 2.1.2020

Математика 5 класс | ID: 11836 | Дата: 26.12.2019

Тест на знание формул вычисления площади и периметра прямоугольника, на умение использовать формулы при решении задач.
Математика 5 класс | Автор: Лобанова ОА | ID: 11731 | Дата: 22.11.2019

Уметь находить делители данного числа; уметь находить кратные данного числа; Уметь находить общие кратные и наименьшее общее кратное чисел; знать и уметь применять признаки делимости;
Математика 5 класс | Автор: Корякина Наталья Анатольевна, МБОУ «Тиксинская СОШ №1» | ID: 11556 | Дата: 27.10.2019

уметь решать задачи на сложение и вычитание
Математика 5 класс | Автор: Корякина Наталья Анатольевна, МБОУ «Тиксинская СОШ №1» | ID: 11403 | Дата: 15.10.2019

вычисление периметра, площади, стороны прямоугольника, квадрата.
Математика 5 класс | Автор: Сайфуллина | ID: 11558 | Дата: 8.10.2019

Тест по теме «Площадь прямоугольника»
Математика 5 класс | Автор: Новикова Марина Евгеньевна | ID: 11557 | Дата: 19.9.2019

Уметь решать задачи на умножение и деление
Математика 5 класс | Автор: Корякина Наталья Анатольевна, МБОУ «Тиксинская СОШ №1» | ID: 11404 | Дата: 27.8.2019

Уметь выполнять сложение, вычитание, умножение и деление многозначных чисел; знать как связаны между собой сложение и вычитание, умножение и деление;
Математика 5 класс | Автор: Корякина Наталья Анатольевна, МБОУ «Тиксинская СОШ №1» | ID: 11402 | Дата: 15.8.2019
Страница 1 из 20
Как решать Задачи по Математике 5 класс (2017) + Примеры, Таблицы
Editor choice
СохранитьSavedRemoved 18

Существует много причин, по которым ребёнок не может решить задачу по математике 5 класс. В большинстве из них он не виноват, поэтому стоит ему помочь разобраться с проблемой. Задачи не такие трудные, но в связи с появлением дробей и уравнений иногда сложно определить способ и верный путь их решения.
Содержание статьи:
Почему инструкция лучше решебника
В этой инструкции вы сможете найти типовые задачи, которые встречаются в курсах математики за 5 класс и разобранное, подробное, пошаговое решение. Это значительно полезнее книг, так как в них собраны далеко не все задачи, а те решения, которые есть, сжаты до минимума. Поэтому пользоваться решебником — порой не самый лучший выход.

Решебник по математике не всегда может дать исчерпывающую информацию
Как правило, при составлении ответов на свои задачи авторы не расписывают подробности и дают решения не ко всем номерам. Возможно, в расчёт идёт тот факт, что ученик способен справиться самостоятельно. Но вдруг ребёнок пропустил тему, что же тогда делать?
Лучший вариант — посмотреть решение типовых задач с пояснениями каждого действия. В этой инструкции собраны самые распространённые примеры, которые вызывают трудности у детей при решении, а также родителей при попытке объяснить задачу.
вернуться к меню ↑ вернуться к меню ↑
Почему важно уметь решать задачи по математике
Математика — точная дисциплина, связанная с вычислениями. Но её часто называют царицей всех наук. Это не просто так. Основное, чему учатся дети — решение конкретно поставленных задач. Это самое важное для развития любого человека.
Для построения правильного ответа на задачу нужно выделить:
- главную мысль;
- заданное условие;
- что требуется найти;
- связь между искомым и данным.

Математика — один из самых важных предметов в школьной программе
На основе этого строится логичное решение с использованием условий для получения требуемого результата. Вместе с этим развивается познавательная активность, логические мышление.
вернуться к меню ↑ вернуться к меню ↑
Какие бывают задачи по математике в 5-ом классе
В 5-ом классе по математике встречается несколько разновидностей задач. Этот год самый важный для ученика, потому что здесь собраны все базовые условия, которые углублённо решаются в следующие годы обучения. Здесь представлен список самых распространённых задач:
- на базовые арифметические действия;
- на скорость, время и расстояние;
- на движение;
- решаемые алгебраическим способом — проценты, дроби, уравнения;
- решаемые геометрическим способом — площадь, длина.

Существует немало различных задач и путей их решения
Для грамотного решения всех типов задач можно составить единый алгоритм:
- Прочитайте вдумчиво, не торопясь полный текст задачи;
- Определите к какому типу она относится;
- На основе этого составьте краткое условие или таблицу;
- Начните читать каждое предложение отдельно, заполняя таблицу или краткое условие;
- Определите вопросом то, что нужно найти;
- Выберите вариант решения и составьте выражение, в результате которого получится ответ;
- Проверьте правильность и соответствие условию;
- Запишите полученный ответ.
Этот алгоритм можно применять ко всем типам задач. В разных заданиях отличаться будут только числа и способ решения.
Далее представлены все типы задач, которые могут встретить пятиклассники в учебниках и задачниках по математике. Все они будут разобраны на двух примерах с подробным разъяснением.
вернуться к меню ↑ вернуться к меню ↑
Задачи на сложение, вычитание, умножение и деление
вернуться к меню ↑
Пример 1
На кухне лежит пакет, в котором 3000 грамм муки. Повар для выпечки из него брал 4 раза муку. В первый раз 250 грамм, во второй 320 грамм, в третий 140 грамм, в четвёртый 690 грамм. Найдите сколько муки осталось в пакете.
Решение
- Для начала запишем краткое условие в виде таблицы. Повар брал муку четыре раза, значит для каждого раза делаем по одной строчке.
- Всего у нас было 3000 грамм. Это ещё одна строка.
- От нас требуют найти остаток, значит — это последняя строка.
- Заполняем таблицу. Какой она получится, смотрите ниже.
Таблица 1 — Краткое условие
| Условие | Количество |
|---|---|
| Было | 3000 |
| Первый раз | 250 |
| Второй раз | 320 |
| Третий раз | 140 |
| Четвёртый раз | 690 |
| Осталось | ? |
- Сделанная таблица наглядно показывает, что для расчёта остатка нужно из 3000 вычесть количество, которое повар забрал всего;
- Для этого сложим количество муки, которое повар израсходовал за четыре раза. Получается такое выражение: 250+320+140+690=1400 грамм;
- Теперь найдём остаток. Для этого из того, что было, вычтем полученное значение — 1400. Получим выражение: 3000-1400=1600 грамм. Это то, что от нас требовалось — найти сколько осталось муки;
- Записываем это в ответ к задаче.
вернуться к меню ↑
Пример 2
В пассажирском поезде 12 вагонов. В каждом из них по 40 мест. Сколько осталось свободных мест, при условии, что в поездку отправились 352 пассажира?
Решение
- Составляем краткое условие. Нагляднее всего будет снова использовать таблицу;
- У нас есть количество вагонов — первая строчка. Количество свободных мест в каждом вагоне — вторая строка. Места, которые заняли пассажиры — третья. Сколько осталось мест — четвёртая;
- Далее заполняем таблицу числами из условия. Что получилось, смотрите ниже;
Таблица 2 — Условие задачи
| Места в вагоне | Количество |
|---|---|
| Кол-во вагонов | 12 |
| Кол-во мест в вагоне | 40 |
| Кол-во пассажиров | 352 |
| Осталось мест | ? |
- Теперь приступаем к вычислениям. Для начала нам нужно узнать сколько всего свободных мест было в вагонах. Для этого умножим количество вагоном на количество свободных мест в каждом. Получается выражение: 40×12=480;
- Для того, чтобы найти сколько осталось свободных мест нужно, из полученного значения вычесть занятые места. Получим выражение: 480-352=128;
- Полученное число — это ответ на вопрос из условия задачи. Записываем его.
Эти задачи самые простые и встречаются в начале учебного года. Используют их авторы учебников для того, чтобы ученик мог вспомнить алгоритм решения и базовые правила.
вернуться к меню ↑ вернуться к меню ↑
Задачи на скорость, время, расстояние
вернуться к меню ↑
Пример 1
За 7 часов теплоход проделал путь в 210 км. Поезд за 4 часа преодолел 420 км. Во сколько раз скорость поезда больше скорости теплохода?
Решение
- Записываем краткое условие. В этом типе задач оно немного отличается от стандартного;
- У нас есть два объекта — теплоход и поезд. Это значит, что в таблице будет две строки;
- Для каждого объекта есть три значения, соответственно, и столбцов будет три;
- Заполняем числами таблицу. Что должно получится смотрите ниже;
Таблица 3 — Краткое условие
| Скорость | Время | Расстояние | |
|---|---|---|---|
| Теплоход | ? | 7 | 210 |
| Поезд | ? | 3 | 360 |
- Приступим к поиску неизвестных. Нам нужно узнать скорость у теплохода и поезда. Для этого используется формула — скорость равна результату деления расстояния на время. Математически записывается так — V=S:T;
- Подставив числа из условия, получаем выражение для скорости теплохода. 210:7=30 км/ч;
- Также поступаем и для расчёта скорости поезда. 360:3=120 км/ч;
- Мы нашли все неизвестные и теперь возвращаемся к главному вопросу задачи. Нам нужно определить во сколько раз скорость поезда превышает скорость теплохода;
- Для этого делим большее значение на меньшее. Получается: 120:30=4;
- В ответ пишем, что скорость теплохода и поезда отличается в 4 раза.
вернуться к меню ↑
Пример 2
Автомобилист за 4 часа проехал 320 километров. Какой путь проделает автомобиль за 8 часов с той же скоростью?
Решение
- Записываем краткое условие. Объект один, значит строка будет одна. Столбцов стандартно три;
- Заполняем числа из условия в таблицу. Что получится смотрите ниже;
Таблица 4 — краткое условие
| Скорость | Время | Расстояние | |
|---|---|---|---|
| Автомобиль | ? | 4 | 320 |
- Ищем неизвестные. В нашем случае нужно найти скорость. Для этого воспользуемся формулой V=S:T. Подставляем числа и получаем: 320:4=80 км/ч;
- После того, как стали известны все значения, переходим к главному вопросу задачи — сколько проедет автобус за 8 часов с той же скоростью;
- Для расчёта используем формулу S=VT. Подставляем числа и получаем: 80×8=640 км;
- Записываем полученное значение в ответ к задаче.
Решение этих задач требует знать основную формулу S=VT. Расшифровывается она так: расстояние равно произведению скорости на время. Из неё вытекают все решения для нахождения неизвестных. Также для упрощения задачи можно рисовать схему.
вернуться к меню ↑ вернуться к меню ↑
Задачи на движение
вернуться к меню ↑
Пример 1
Расстояние между двумя городами 125 километров. В одно и то же время выезжают два велосипедиста навстречу. Скорость первого велосипедиста 10 км/ч. Второй едет со скоростью 15 км/ч. Через какое время они встретятся?
Решение
- Начинаем с составления краткого условия. Лучше всего оформить в качестве таблицы;
- Велосипедиста два— значит нужны 2 строки. Столбцов стандартно 3. Но в этом типе задач у нас будут общие показатели. То есть, расстояние и время всегда одно сразу для всех строк;
- Заполняем таблицу числами. Что должно получится смотрите в ниже;
Таблица 5 — краткое условие
| Скорость | Время | Расстояние | |
|---|---|---|---|
| 1 велосипедист | 10 | ? | 125 |
| 2 велосипедист | 15 | ? | 125 |
- Теперь переходим к расчётам. Логично, что для встречи велосипедисты должны проехать в сумме весь путь. Необязательно одинаковое расстояние, так как оно зависит от скорости каждого из них;
- Нам нужно посчитать какое расстояние они преодолевают в час. Для этого сложим скорости первого и второго. Получаем выражение: 10+15=25 км/ч;
- Для расчёта времени через которое они встретятся нужно воспользоваться формулой T=S:V. Подставляем числа и получаем выражение: 125:25=5 ч;
- Соответственно, велосипедисты пересекутся между собой через 5 часов. Записываем это в ответ.
вернуться к меню ↑
Пример 2
Расстояние, на котором между собой находятся два города — 600 км. Из них одновременно на встречу друг другу выехали два автомобиля. В пути они встретились через 5 часов. Найдите скорость первого автомобиля, если известно, что второй ехал со скоростью 80 км/ч.
Решение
- Составим таблицу, в которой ситуация из условия будет наглядно представлена;
- Два автомобиля — две строки. Стандартное количество столбцов — три;
- Заполняем числами из условия. Что должно получится, смотрите ниже;
Таблица 6 — краткое условие
| Скорость | Время | Расстояние | |
|---|---|---|---|
| 1 автомобиль | ? | 5 | 600 |
| 2 автомобиль | 80 | 5 | 600 |
- Переходим к расчётам. Для нахождения скорости первого автомобиля нам нужно знать, сколько километров он проехал. Найти это можно, вычтя из общего пути расстояние, которое проехал второй до их встречи;
- Используем формулу S=VT. Подставляем числа из таблицы, получаем выражение: 80×5=400 км. Это расстояние прошёл второй автомобиль до встречи с первым. Значит, первый проехал всего: 600-400=200 км;
- Теперь можно найти скорость первого автомобиля. Используем формулу V=S:T. Подставляем числа: 200:5=40 км/ч;
- Полученное значение — ответ на главный вопрос задачи. Записываем его.
Если вас смущает время, которое написано один раз для всех объектов, то можно поступить следующим образом. Записывайте его отдельно к каждой строке и рядом нарисуйте отрезок, который снизу отмечен расстоянием, а сверху подписан временем.
вернуться к меню ↑ вернуться к меню ↑
Задачи, решаемые алгебраическим способом
вернуться к меню ↑
Пример 1
Из цистерны отлили 80 литров молока, в нем осталось на 240 литров больше, чем отлили. Сколько литров молока было в цистерне с самого начала?
Решение
- Начинаем с составления краткого условия в виде таблицы. В подобных типовых задачах нужно обозначать неизвестное за «x»;
- Потребуются три строки: сколько молока было, сколько его отлили и сколько осталось;
- Заполняем числами таблицу;
Таблица 7 — краткое условие задачи
| Было | Х |
|---|---|
| Отлили | 80 |
| Осталось | 240+80 |
- Приступаем к расчётам. Нам нужно узнать, сколько было молока изначально. Для этого составляем уравнение. От начального количества вычитаем отлитое и получаем остаток;
- Математически получаем такую запись: x-80=240+80;
- Начинаем решение с того, что считаем всё, что можно посчитать. В данном случае складываем правую часть уравнения. 240+80=320. Теперь уравнение имеет вид: x-80=320;
- Теперь находим «x». Используем базовое правило математики и получаем следующее: x=320+80. Считаем правую часть и получаем: x=400;
- Возвращаемся к началу и смотрим, что мы обозначили за «x». В этом примере за икс мы взяли объём молока, который был изначально. То есть, изначально было 400 литров молока;
- Записываем полученное значение в ответ.
вернуться к меню ↑
Пример 2
Первое слагаемое на 52 больше второго слагаемого, а второе слагаемое на 14 меньше третьего слагаемого. Сумма трех слагаемых равна 327. Найдите каждое слагаемое.
Решение
- Записываем краткое условие в виде таблицы;
- Потребуется четыре строки, так как нам дали три слагаемых и их сумму;
- Заполняем таблицу числами, обозначив за икс последнее слагаемое. Выбираем третье, потому что от него зависят все остальные;
Таблица 8 — краткое условие задачи
| 1 слагаемое | (x-14)+52 |
|---|---|
| 2 слагаемое | x-14 |
| 3 слагаемое | x |
| Сумма | 327 |
- Приступаем к расчётам. Для нахождения слагаемых нужно решить уравнение, после чего число подставить в выражения из таблицы.
- Уравнение составляется исходя из условия – три слагаемых и сумма – складываем значения из второго столбца таблицы и приравниваем это к сумме.
- Получится такое выражение: (x-14)+52+(x-14)+x=327.
- Открываем скобки и упрощаем выражение: 3x+24=327.
- Переносим числа в правую часть: 3x=303
- Считаем икс: 303:3=101.
- Теперь подставляем число 101 в таблицу вместо икса.
- Получается третье слагаемое равно 101; второе: 101-14=87; первое: 87+52=139.
- Эти числа записываем в ответ. Легко проверить правильность решения просто сложив эти значения. Если пример получается правильный, то и решено всё верно.
Для правильного решения этих типовых задач необходимо ничего не напутать с иксом. Лучше потратить больше времени и сразу всё проверить, чем переделывать задание сначала. Неправильное обозначение повлечёт за собой ошибку на протяжении всего решения
вернуться к меню ↑ вернуться к меню ↑
Задачи, решаемые геометрическим способом
вернуться к меню ↑
Пример 1
В доме 4 двери. Ширина каждой 1 метр, высота — 2 метра. Сколько нужно белил, чтобы покрасить их с обеих сторон, при условии, что на 1 квадратный метр поверхности требуется 100 грамм белил? Ответ дайте в граммах.
Решение
- Для решения нужно вычислить площадь каждой двери, которую нужно покрасить. Для этого используем формулу площади прямоугольника – S=ab, где a и b – длины сторон. Подставляем числа из условия и получаем: S=2×1=2 м2;
- Далее умножаем площадь на 2, потому что каждую дверь нужно окрасить с двух сторон. Получаем 2×2=4 м2. То есть, покрасочная площадь каждой двери равна 4 квадратным метрам;
- Посчитаем общую площадь для всех дверей. Для этого умножаем площадь одной на их количество: 4×4=16 м2;
- Главный вопрос задачи — сколько потребуется белил для всех дверей? Чтобы посчитать умножаем количество, требующееся на 1 квадратный метр на всю площадь: 100×16=1600 грамм;
- Записываем это значение в ответ.
вернуться к меню ↑
Пример 2
Площадь прямоугольника 192 квадратных сантиметра, длина одной из сторон — 16 см. Найдите периметр прямоугольника.
Решение
- Для начала нужно посчитать другую сторону прямоугольника. Делается это с помощью формулы площади: S=ab, где a и b — длины сторон. Подставляем числа и получаем: 192=16*a. Отсюда получается, что вторая сторона — 12 см;
- Для нахождения периметра воспользуемся формулой P=2(a+b). Подставляем числа и получаем: P=2(16+12)=2×28=56 см;
- Найденное значение записываем в ответ.
Для решения геометрических задач нужно знать наизусть все формулы площадей и периметров. Без этого не получится даже приступить к решению задания.
вернуться к меню ↑ вернуться к меню ↑
Нужен ли ребёнку репетитор по математике в пятом классе?
После перехода в средний этап школы у ребёнка может упасть успеваемость по некоторым предметам, в том числе и по математике. Более того математика — самый проблематичный предмет для детей. Некоторые родители сразу бьют тревогу и ищут репетиторов, чтобы исправить эту ситуацию.
На самом деле, не стоит делать поспешных выводов. Для начала нужно определить причину падения успеваемости. Возможно, некоторые из новых учителей просто халатно относятся к преподнесению нового учебного материала. Другие преподаватели не могут найти особый подход к ребёнку в связи с ограничением по времени.

У многих детей в школе возникают сложности с изучением математики
Это не значит, что ваш ребёнок неспособный к определённым дисциплинам. Попробуйте объяснить ему материал самостоятельно, ведь именно вы знаете своё чадо лучше других. Если и это не помогло, то обращайтесь к помощи репетитора.
Главная задача специалиста — найти персональный подход к каждому ученику. Они смогут максимально эффективно и просто объяснить ребёнку тему в зависимости от особенностей его восприятия и склада ума.
Перед обращением убедитесь, что ухудшение оценок произошло только по нескольким взаимосвязанным предметам, а не в целом. Если успеваемость сильно упала в общем плане, то скорее всего ребёнок ленится. Связано это может быть со скукой на уроках и утратой интереса к учёбе. В таком случае, поговорите с ним, объясните, что это очень важно и пригодится в жизни, приводя аргументы и наглядные примеры.
Конечно, если это связано, например, с пропуском занятий по причине болезни, или в школе неправильно преподносится материал, то стоит задуматься о найме репетитора. Он поможет в кратчайшие сроки улучшить результаты ребёнка.
вернуться к меню ↑ вернуться к меню ↑
Как решить проблемы с математикой
Как только у ребёнка появляются проблемы с математикой родители почему-то начинают думать, что причина заключается в плохой предрасположенности к точным наукам. Потому что формулы вроде бы знает, простые примеры решить тоже может, но каждая контрольная и самостоятельная работа превращается в целое испытание для всей семьи. Все сидят в ожидании результатов. Никогда нельзя сказать точно какую оценку получит ребёнок — четвёрку или двойку.

Дети часто получают плохие отметки именно по математике
Также много жалоб по типу: занимаемся все выходные напролёт, учим эту математику, учим, а в итоге всё равно результат прежний. На самом деле, причина такого плохого восприятия — отсутствие адекватных причин заниматься всеми этими цифрами. Большинство родителей сходятся во мнении, что ребёнок просто гуманитарий, главное — литература, история, обществознание, а математика неважна.
вернуться к меню ↑
Гуманитариям математика не нужна?
Это огромная ошибка, ведь для лучшего восприятия точных наук этому самому «гуманитарию» нужно лишь вдохновение и цель. Отлично будет, если ребёнку объяснить, что математика — это такая же наука, как и любая другая, и она не ограничивается уравнениями и задачами. Это нечто большее. Математика позволяет изменить мышление, воспринимать старые вещи по-новому.
Главная проблема всех гуманитариев, которые имели проблемы с математикой — это логика. Для составления, например, грамотной и структурированной статьи нужно руководствоваться не только правилами русского языка, но и логикой изложения мысли. Все части должны быть связаны между собой, в то же время, должны легко читаться отдельные фрагменты.
Именно логическое мышление в первую очередь развивает математика и воспринимать это нужно, как возможность расширения кругозора и свежего взгляда на старое. Также точные науки помогают дисциплинировать свой ум и комплексно подходить к решению поставленных задач.
вернуться к меню ↑
Математика — сложный предмет
Самая популярная отговорка заключается в том, что математика — самый сложный предмет из всех. Нет, на самом деле это одна из самых простых и понятных дисциплин. Для сравнения, возьмите наш богатый русский язык.
Мало того, что в нём существует немало правил орфографии, пунктуации, стилистики, так ещё и исключения есть почти в каждом правиле. Вот уж где нужно запоминать «тонну» информации.
В то же время в математике существуют базовые правила, на которых строятся все остальные. То есть, более сложное всегда можно привести к простому. Всё построено на железной логике, и, следуя этим правилам, вы сможете решить задачи, которые казались на первый взгляд непосильными.
Вспомните, как учат всех детей. Для того, чтобы научить их писать, сначала нужно выводить палочки, точки, изгибы. Потом уже буквы, а из букв — простые слова, из слов — предложения.
Начните изучать математику с самых простых уравнений
В математике с самого начала всё объясняется на пальцах или предметах. При этом, за то же самое время, потраченное на русский язык и на математику, прогресс в изучении второй будет больше. Например, считать учатся дети на яблоках, конфетках.
Используйте это и для решения более сложных задач. В пятом классе аналогии привести не составит труда. Это поможет ребёнку ассоциировать вычисления не с сухими числами, а, например, с мандаринами.
вернуться к меню ↑ вернуться к меню ↑
Формула спокойствия
Часто плохие оценки становятся причиной ссор между родителями и детьми. Это категорически неправильно. Вместо того, чтобы высказывать ребёнку, что он «ленится», «не думает о будущем» да и в общем «туго соображает», следует отвести от неудачи или помочь исправиться с ней.
Но под помощью подразумевается не «вдалбливание» и «зубрёжка» неинтересных формул и правил. Следует возбудить интерес к теме, которая была плохо воспринята. Да и к тому же поставить правильную цель ребёнку. Не нужно говорить, что от оценок зависит его будущее. Вообще не зацикливайте внимание на оценках.
По исследованиям российских психологов дети, которые хотели стать врачами, инженерами и просто хорошими людьми, быстро повышали свою успеваемость. А те ученики, которым с первого класса «вдалбливают» в голову знания, думали только о том, как не стать худшим в классе, и уделяли своим отметкам слишком большое внимание.
Лучшим вариантом по-прежнему остаются занятия с репетитором. Он сохранит нервы, и вам, и ребёнку. Обеспечивая нужное количество времени на обучение и выбрав правильный подход, ученик станет показывать результаты лучше прежнего. Но, моментально отличником вашего ребёнка это не сделает.
Надеемся, что вы смогли найти решение задач, которое искали. Также для понимания темы рекомендуем посмотреть видео по этой теме от организаторов специальной математической школы федерального уровня «Аристотель».
8.5 Общий Балл
Некоторые ученики, как пятых, так и других классов, часто сталкиваются с проблемами в изучении математики. В этом случае родителям не стоит впадать в панику. Следует уделить больше внимания детальному разбору примеров и задач. Если это не улучшит успеваемость, есть смысл обратиться за помощью к репетитору.
Плюсы
- Подробные инструкции помогут разобраться в решении задач и примеров
- Для изучения математики можно пользоваться решебниками
Минусы
- Полученных знаний в школе не всегда достаточно для понимания предмета
Добавить свой отзыв
Задания на лето по математике 5 класс
Задания на лето по математике
5 класс
Составитель:
учитель математики
МАОУ СОШ № 45
Панкратова О. В.
Г. Тюмень — 2017
Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели.
А. Маркушевич
Дорогой ученик!
Занимаясь летом, ты постепенно сможешь повторить курс математики за 5 класс. А значит, обретёшь уверенность перед новым учебным годом!
Желаю успехов!

И не забывай отдыхать!!!
Математику уж затем учить следует,
что она ум в порядок приводит.
М. В. Ломоносов
Ребята!
Работу нужно выполнять в отдельной тетради, которую вы подписываете, как тетрадь для летних заданий по математике. Старайтесь выполнять задания каждый день – в среднем по 3 задания в день по каждой теме 5 класса, не затягивайте. Занятия начинайте с повторения теории, и только потом приступайте к заданиям. Будьте внимательны при выполнении каждого задания, оформляйте работу по всем правилам ведения тетради и правилам решения заданий по математике (столбики, краткая запись,…).
Уважаемые родители!
Не отказывайте своим детям в помощи, если они к Вам обратятся, ведь их развитие – это Ваше будущее.
Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил
к своему образованию.
Я. А. Каменский
Работа № 1 по теме
«Обозначение натуральных чисел.»

Работа № 2 по теме
«Отрезок. Длина отрезка. Треугольник.»

Работа № 3 по теме
«Плоскость. Прямая. Луч.»

Работа № 4 по теме
«Шкалы и координаты.»

Работа № 5 по теме «Меньше или больше.»
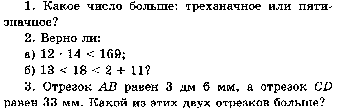
Работа № 6 по теме
«Сложение натуральных чисел.»

Работа № 7 по теме «Вычисления.»

Работа № 8 по теме «Числовые и буквенные выражения.»
Работа № 9 по теме
«Буквенная запись свойств сложения и вычитания.»

Работа № 10 по теме «Уравнения.»
Работа № 11 по теме
«Умножение натуральных чисел.»

Работа № 12 по теме «Деление.»

Работа № 13 по теме «Деление с остатком.»

Работа № 14 по теме
« Упрощение выражений.»

Работа № 15 по теме « Порядок выполнения действий.»
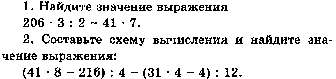
Работа № 16 по теме « Квадрат и куб числа.»
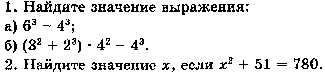
Работа № 17 по теме « Формулы.»

Работа № 18 по теме « Площадь.»

Работа № 18 по теме « Единицы измерения площадей.»

Работа № 19 по теме
«Прямоугольный параллелепипед.»

Работа № 20 по теме «Объем.»

Работа № 21 по теме «Окружность и круг.»

Работа № 22 по теме «Доли. Обыкновенные дроби.»

Работа № 23 по теме «Сравнение дробей.»

Работа № 24 по теме «Сравнение дробей.»

Работа № 25 по теме «Сложение и вычитание дробей с одинаковыми знаменателями.»

Работа № 26 по теме «Деление и дроби.»
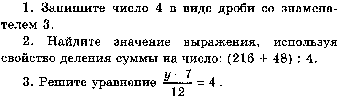
Работа № 27 по теме «Смешанные числа.»

Работа № 28 по теме
«Сложение и вычитание смешанных чисел.»

Работа № 29 по теме
«Десятичная запись дробных чисел.»

Работа № 30 по теме «Сравнение десятичных дробей.»
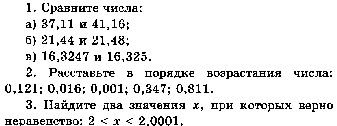
Работа № 31 по теме
«Сложение и вычитание десятичных дробей.»

Работа № 32 по теме «Округление чисел.»

Работа № 33 по теме
«Умножение десятичных дробей на натуральное число.»

Работа № 34 по теме «Деление десятичных дробей на натуральное число.»
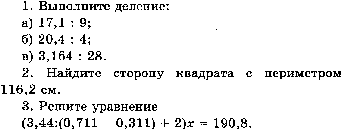
Работа № 35 по теме
«Умножение десятичных дробей.»

Работа № 36 по теме
«Деление десятичных дробей.»

Работа № 37 по теме
«Среднее арифметическое.»

Работа № 38 по теме «Проценты.»

Работа № 39 по теме «Угол.»

Работа № 40 по теме
«Измерение углов. Транспортир.»

Работа № 41 по теме
«Круговые диаграммы.»

Проверь свои знания – реши итоговый тест за курс 5 класс


Математика уступает свои крепости
лишь сильным и смелым.
А.П. Конфорович
Ну вот и всё!
Поздравляю!
Ты прошёл все испытания!
В новом учебном году ты получишь много хороших оценок, потому что — ты трудолюбивый и ответственный!
С нетерпением жду встречи с тобой
1 сентября 2017 года!
Источники:
1. Контрольные и самостоятельные работы по математике 5 класс: к учебнику Н. Я. Виленкина и др. «Математика 5 класс» / М. А. Попов. -7-е изд., стереотип. – М.: Издательство «Экзамен», 2012.
2. Контрольно-измерительные материалы. Математика. 5 класс/ сост. Л.П. Попова. 3-е изд., перераб.- М.: ВАКО, 2014.
Тесты по математике 5 класс
Задание 1
Найдите значение выражения: (3487 + 4847 — 12 * 194) : 182
Задание 2
Какое из чисел при делении на 356 дает остаток 254?
| 1) 12486 | 2) 5238 | 3) 7138 | 4) 8392 |
Задание 3
Чему равен периметр четырех угольника на рисунке?
| 1) 40 см 3 мм | 2) 41 см 29 мм |
| 3) 31 см 43 мм | 4) 52 см 11 мм |
- Решение
- 1) 40 см 3 мм
Задание 4
У какого из уравнений корнем является число 11.
| 1) 12x — 11x + 9 = 25 | 2) 591 : y — 16 = 181 |
| 3) 293 — 18a = 95 | 4) 3b + b + 24 = 48 |
- Решение
- 3) 293 — 18a = 95
Задание 5
Вычислите чему равно 15% от 120.
Задание 6
В первый день путешественники преодолели три части пути, во второй две, а в третий день еще три части пути. Какое расстояние преодолели путешественники во второй день, если весь путь составлял 384 км.
| 1) 84 км | 2) 96 км | 3) 102 км | 4) 48 км |
- Решение
- 2) 96 км
Задание 7
В первый день Вова прочитал 36 страниц, что составляло 3/11 всех страниц книги. Сколько всего страниц в книге?
| 1) 132 | 2) 312 | 3) 128 | 4) 164 |
Задание 8
Какую из формул следует использовать, чтобы вычислить объем прямоугольного параллелепипеда.
| V = a/bc | V = c * a/b | V = abc | V = (abc)² |
Задание 9
Заверши цепочку, выбрав правильное число
Задание 10
Какое из чисел, приведенных ниже наибольшее.
| 1,0009 | 1,0003 | 1,001 | 1,00098 |
Задание 11
Чему равна разность значений выражений 3,004 * 0,6 и 0,0531 : 3.
| 1) 1,7847 | 2) 0,438 | 3) 2,003 | 4) 1,8563 |
Задание 12
Определите координату точки C, если A(9,9), а B(19,3) и AC = CB
| 1) 9,2 | 2) 14,6 | 3) 13,1 | 4) 12,8 |
Олимпиада по математике для 5 класса
Муниципальный этап областной олимпиады школьников
по математике
5 класс
Максимальный балл — 35
1. Решите задачу (7 баллов)
Можно ли выписать в ряд натуральные числа от 1 до 60 так, чтобы разность любых двух соседних чисел была не меньше 30?
2. Решите задачу (7 баллов)
На каждые две девочки в классе приходится один мальчик. Если всего в классе двадцать семь учеников, то сколько из них девочек?
3. Решите задачу (7 баллов)
Внутри круга отметили точку. Можно ли разрезать круг на три части так, чтобы из них можно было сложить новый круг, у которого эта точка окажется в его центре?
4. Решите задачу (7 баллов)
Деревянный куб покрасили снаружи белой краской. Каждое ребро куба разделили на пять равных частей, после чего куб распилили так, что получились маленькие кубики, у которых ребро в пять раз меньше, чем у исходного куба. Сколько получилось неокрашенных кубиков.
5. Решите задачу (7 баллов)
До царя Гороха дошла молва, что кто-то из троих богатырей убил Змея Горыныча. Царь приказал всем троим богатырям явиться ко двору. И молвили они:
Илья Муромец: «Змея убил Добрыня Никитич».
Добрыня Никитич: «Змея убил Алеша Попович».
Алеша Попович: «Я убил змея».
При этом оказалось, что один из них сказал правду, а двое слукавили. Кто убил змея?
Примерные варианты решений и оценка задач
Муниципального этапа областной олимпиады школьников по математике
5 класс
Задача №1 Можно ли выписать в ряд натуральные числа от 1 до 60 так, чтобы разность любых двух соседних чисел этого ряда была не меньше 30?
Решение: Заметим, что последнее число 60, тогда перед ним может быть число 30, 29, 28, 27, … 3, 2, 1. Числа, которые будут отличаться от этих чисел не меньше, чем на 30 образуют последовательность: 31, 32, 33, …57, 58, 59, 60.
Ответ: можно, например: 30, 60, 29, 59, 28, 58, …, 3, 33, 2, 32, 1, 31.
Замечание по оцениванию
-Если указан весь ряд натуральные числа от 1 до 60 такой, что разность любых двух соседних чисел не меньше 30, то задание оценивается в 7 баллов
-Если указана только часть ряда, то задание оценивается в 4 балла.
Задача №2 На каждые две девочки в классе приходится один мальчик. Если всего в классе двадцать семь учеников, то сколько из них девочек?
Решение: На каждые две девочки приходится один мальчик, значит детская группа состоит из трех человек. В классе 27 учеников. Следовательно, детских групп будет 9, и в каждой такой группе по две девочки. Значит девочек 18.
Ответ: в классе 18 девочек.
Замечание по оцениванию
-Верное решение оценивается -7 баллов.
-Если идея решения верна, но допущена вычислительная ошибка — 0 баллов.
Задача №3 Внутри круга отметили точку. Можно ли разрезать круг на три части так, чтобы из них можно было сложить новый круг, у которого эта точка окажется в его центре?
Решение: Из большого круга вырежем два одинаковых кружка радиуса r – один с центром в отмеченной точке A, а другой – с центром в точке O (центре круга). Радиус r нужно взять таким, чтобы кружки не перекрывались и не выходили за пределы исходного круга. Эти кружки поменяем местами.
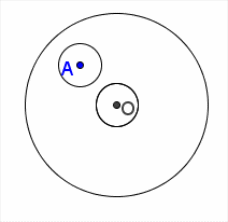
Ответ: да, можно.
Замечание по оцениванию
-Если представлено полное решение с рисунком -7 баллов.
-Если представлен верный рисунок без объяснения, то -5 баллов.
Задача №4 Деревянный куб покрасили снаружи белой краской. Каждое ребро куба разделили на пять равных частей, после чего куб распилили так, что получились маленькие кубики, у которых ребро в пять раз меньше, чем у исходного куба. Сколько получилось неокрашенных кубиков.
Решение. После распиливания получилось 125 кубиков. Окрашенные грани имеют 98 кубиков. Значит, неокрашенных кубиков 27.
Ответ: 27.
Замечание по оцениванию
-Если решение верное, с указанием, как можно вычислить количество неокрашенных граней, то -7 баллов.
-Если решение не доведено до конца или содержит вычислительную ошибку, то — 0 баллов.
Задача №5 До царя Гороха дошла молва, что кто-то из троих богатырей убил Змея Горыныча. Царь приказал всем троим богатырям явиться ко двору. И молвили они:
Илья Муромец: «Змея убил Добрыня Никитич».
Добрыня Никитич: «Змея убил Алеша Попович».
Алеша Попович: «Я убил змея».
При этом оказалось, что один из них сказал правду, а двое слукавили. Кто убил змея?
Решение. Рассмотрим все возможные варианты.
1)Если Алеша Попович сказал правду, тогда Добрыня Никитич и Илья Муромец слукавили. Из этого следует противоречие: «Алеша Попович убил змея» одновременно является истинным и ложным высказыванием.
2)Если Добрыня Никитич сказал правду, то Алеша Попович и Илья Муромец слукавили. В этом случае тоже получим противоречие.
3)Остается случай, когда правду сказал Илья Муромец. В этом случае утверждение «Змея убил Добрыня Никитич» истинно, а утверждения «Змея убил Алеша Попович» и «Я убил змея» — ложны. Этот случай удовлетворяет условию задачи.
Ответ: Змея убил Добрыня Никитич.
Замечание по оцениванию
-Правильный ответ и верные рассуждения оцениваются в 7 баллов.
-Перебор возможных случаев до первого удовлетворяющего оценивается в 4 балла. (Так как не доказано, что других случаев нет).
-Если указан ответ и доказано что он удовлетворяет условиям задачи, то- 3 балла.
-Если дан один ответ без рассуждений. То такое решение оценивается-2 балла.
-За все остальные решения- 0 баллов.